考慮一個社交網(wǎng)絡(luò),用網(wǎng)絡(luò)中的頂點代表人,網(wǎng)絡(luò)中的邊代表兩人互相認(rèn)識,而網(wǎng)絡(luò)中一群相互認(rèn)識的人,我們可以用一個由相應(yīng)頂點兩兩連接構(gòu)成的子圖表示,并稱之為團(tuán)。如果想知道一個社交網(wǎng)絡(luò)中有哪些共同朋友的群體以及其中最大的群體是哪個,我們該如何搜索尋找呢?這便是著名的最大團(tuán)問題(Maximum Clique Problem),它屬于一類NP難(NP-hard)問題。在計算復(fù)雜度理論中,如果求解一個問題的時間T隨輸入大小n呈多項式增長,即T(n) = O(nk),則稱該問題為Polynomial復(fù)雜度問題,即P問題,這類問題容易求解。如果一個問題的解可以在多項式時間內(nèi)被猜測和驗證,則該問題稱為 Nondeterministic Polynomial復(fù)雜度問題,簡稱NP問題,Nondeterministic意味著沒有可遵循的特定規(guī)則來猜測該問題的解,一般認(rèn)為不存在精確算法可以高效求解它。著名的整數(shù)質(zhì)因子分解就是一個NP問題。NP難問題本身不是NP問題,但是如果任何一個NP難問題被證明是一個P問題,那么所有的NP問題就一定是P問題,即P=NP。(目前P=NP并未得到證明,且多數(shù)人相信P≠NP。)在圖論中,最大團(tuán)問題可用于社交網(wǎng)絡(luò)分析,以識別具有共同興趣、愛好或信仰的人群,除此之外,最大團(tuán)問題在計算化學(xué)、生物信息學(xué)等領(lǐng)域也有諸多應(yīng)用。
最大團(tuán)問題或團(tuán)問題可以等價地轉(zhuǎn)化為無向圖上的獨立集問題(Independent Set Problem)。它描述的是一個無向圖中那些由兩兩不相鄰的頂點所組成的集合。對于一張由V個頂點,E條邊構(gòu)成的圖G(V, E),它的某一個獨立集S是由圖中若干頂點組成的,且要求S中任意兩個頂點之間沒有邊的連接,每一個獨立集所包含的頂點數(shù)目被定義為該獨立集的基數(shù),其中基數(shù)最大的獨立集則稱之為圖G(V, E)的最大獨立集。由于無向圖中的一個團(tuán)同時也是該無向圖補圖中的一個獨立集,因此最大獨立集問題與最大團(tuán)問題在計算復(fù)雜度上是相互等價的。(在圖論中,補圖是指將原圖中相鄰邊刪去,不相鄰邊連接后形成的圖。)
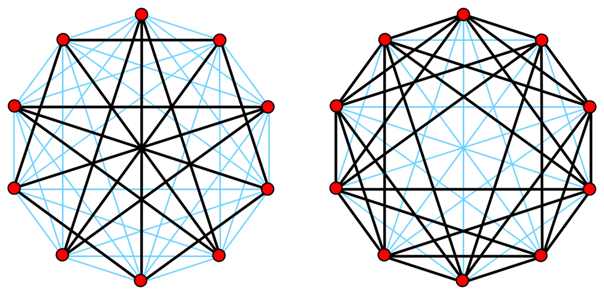
圖2:十頂點彼得森圖(左側(cè))及其補圖(右側(cè))
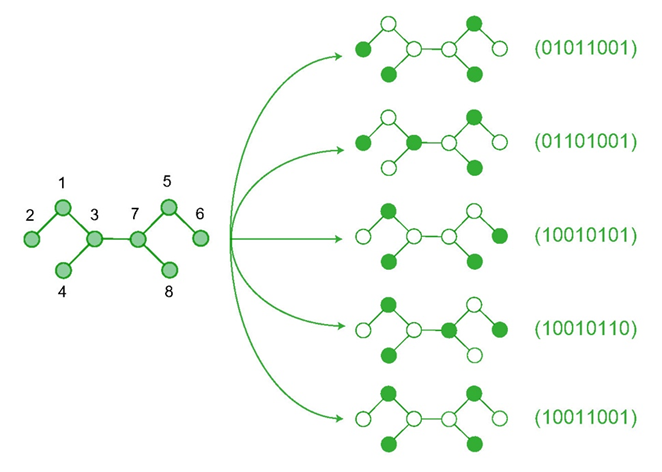
圖3:圖G(8,7)的5個最大獨立集
以圖3中圖G(8, 7)為例,我們將不屬于獨立集的空心點用二進(jìn)制數(shù)0來表示,將屬于獨立集的實心點用二進(jìn)制數(shù)1來表示,經(jīng)過計算我們發(fā)現(xiàn)實心點個數(shù)最多為4個,例如圖中的5種最大獨立集(圖3中右側(cè)所示),可用8位二進(jìn)制數(shù)表示。解決獨立集問題或最大獨立集問題在經(jīng)濟(jì)學(xué)、生物學(xué)、計算機視覺等領(lǐng)域有著廣泛的應(yīng)用。目前對于線圖、平面圖、樹圖等典型結(jié)構(gòu),尋找它們所有的最大獨立集是一個Polynomial復(fù)雜度問題, 即P問題,可以用經(jīng)典算法高效解決。然而,對于一般圖,枚舉或者計算其最大獨立集數(shù)量已經(jīng)被證明是NP難問題[1]。因此,計算機科學(xué)家們的普遍共識是:不存在精確求解一般圖最大獨立集問題的高效算法。因此如何利用量子計算的優(yōu)勢高效尋找一般圖中的獨立集,并進(jìn)一步探索其最大獨立集的問題是一個非常有趣和重要的問題。最近人們發(fā)現(xiàn)求解獨立集問題可以自然地映射為一類求解哈密頓量基態(tài)的問題,然后利用量子絕熱演化來獲得基態(tài)。而隨著實驗技術(shù)的不斷發(fā)展,操控量子系統(tǒng)作絕熱演化已經(jīng)成為可能[2-3]。
絕熱量子計算
在過去的幾十年里,由于量子絕熱算法在解決一般基態(tài)問題方面比經(jīng)典算法具有潛在的加速能力,因此人們付出了巨大的努力來設(shè)計和擴展量子絕熱算法的能力,這些算法在計算化學(xué)、材料科學(xué)、機械制造等領(lǐng)域有著廣泛的應(yīng)用。
絕熱量子計算的基本思想是:首先設(shè)計一個目標(biāo)哈密頓量HP使得它的基態(tài)是我們所感興趣的問題的解(它是未知的因此無法直接制備)。然后,我們再設(shè)計一個簡單的哈密頓量HB,它的基態(tài)不但已知而且實驗上易于制備。在實驗中,我們將系統(tǒng)初始化為哈密頓量HB而且讓其處于基態(tài)。接下來,通過施加外場的方式驅(qū)動該簡單哈密頓量HB作絕熱演化,使其緩慢演化為目標(biāo)哈密頓量HP。根據(jù)絕熱量子理論,系統(tǒng)在絕熱演化過程中將會一直保持在基態(tài),所以當(dāng)演化結(jié)束后,系統(tǒng)所處的最終狀態(tài)即為目標(biāo)哈密頓量HP的基態(tài),這正是該問題的解。

圖4:系統(tǒng)的含時哈密頓量H(t)。t為時間參量,初始時t為0,演化結(jié)束時t為1。
絕熱量子計算的時間復(fù)雜度是指完成絕熱演算所需的時間,與哈密頓量的本征能隙有關(guān)。具體地說,如果系統(tǒng)處于基態(tài),在絕熱演化過程中,基態(tài)與第一激發(fā)態(tài)之間的能隙Δ將給出系統(tǒng)演化速度的上界,當(dāng)Δ越小時,系統(tǒng)的演化速度就越慢。整個算法的運行時間可以被約束為:
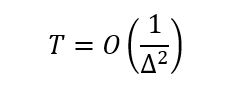
這里Δ代表H(t)的最小能縫,如圖5所示。
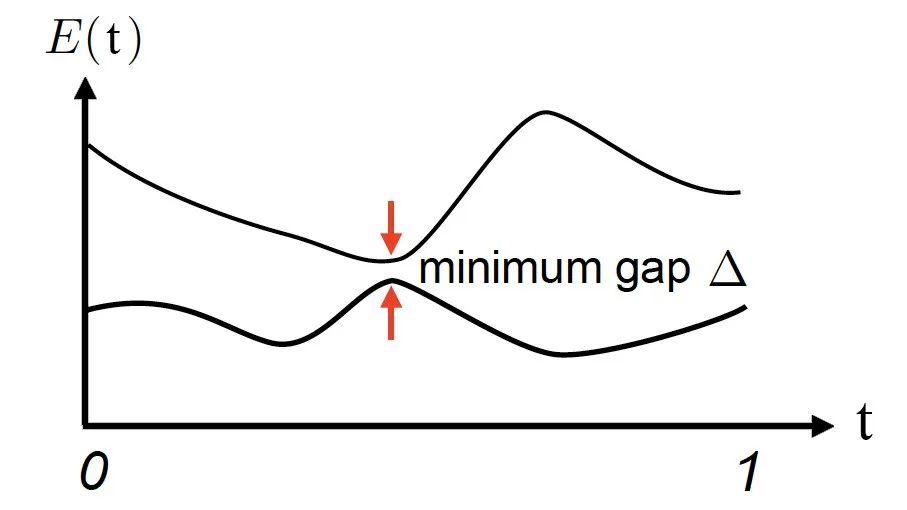
圖5:絕熱演化過程中系統(tǒng)能量E(t)隨時間t的演化
雖然上述傳統(tǒng)的由HB到HP的絕熱演化方案簡單且常用,但如何選擇合適的初始哈密頓量HB使得能隙Δ盡量大仍是一項具有挑戰(zhàn)性的任務(wù)。對于大多數(shù)的選擇,能隙Δ會隨系統(tǒng)大小n指數(shù)減小,這樣得到的量子絕熱算法是指數(shù)慢的,和相應(yīng)的經(jīng)典算法比沒有優(yōu)越性。
幸運的是,對于獨立集問題,我們可以成功地避開這個困難。對應(yīng)圖G(V, E),我們構(gòu)建如下多體哈密頓量其目標(biāo)哈密頓量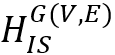 ,
,
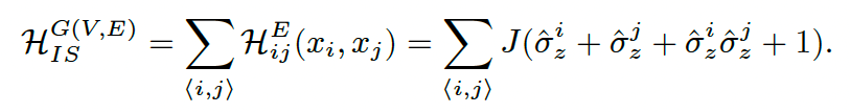 這個哈密頓量的基態(tài)是簡并的,它們和圖G(V, E)的獨立集一一對應(yīng)。有別于傳統(tǒng)的絕熱演化方案,我們將哈密頓量
這個哈密頓量的基態(tài)是簡并的,它們和圖G(V, E)的獨立集一一對應(yīng)。有別于傳統(tǒng)的絕熱演化方案,我們將哈密頓量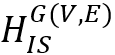 同時設(shè)置為初始和目標(biāo)哈密頓量,在絕熱演化中每一個自旋緩慢旋轉(zhuǎn)。由于基態(tài)簡并,系統(tǒng)在演化中會等效地感受到一個非阿貝爾規(guī)范勢(Non-Abelian Gauge Field)或非阿貝爾貝里聯(lián)絡(luò)(Non-Abelian Berry Connection)。這樣一來,一個初始的易于制備的系統(tǒng)基態(tài)(如直積態(tài)|0??n)將演化成為包含哈密頓量
同時設(shè)置為初始和目標(biāo)哈密頓量,在絕熱演化中每一個自旋緩慢旋轉(zhuǎn)。由于基態(tài)簡并,系統(tǒng)在演化中會等效地感受到一個非阿貝爾規(guī)范勢(Non-Abelian Gauge Field)或非阿貝爾貝里聯(lián)絡(luò)(Non-Abelian Berry Connection)。這樣一來,一個初始的易于制備的系統(tǒng)基態(tài)(如直積態(tài)|0??n)將演化成為包含哈密頓量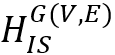 所有基態(tài)(對應(yīng)獨立集問題所有解)的相干疊加態(tài)∑an|gn?,最后,我們通過量子投影測量讀出這個波函數(shù)中包含的解的信息,從而解決相應(yīng)的獨立集問題。這便是我們最近實驗工作中用于求解獨立集問題的量子算法的基本演算流程。 我們稱這個與傳統(tǒng)的絕熱演化算法不同的方法為非阿貝爾絕熱量子混合算法[4],在解決獨立集問題上的它具有兩個獨特優(yōu)勢:(1)在絕熱演化過程中,系統(tǒng)基態(tài)和第一激發(fā)態(tài)之間的能隙Δ是一個保持不變的常數(shù)4J,其中J是一個描述系統(tǒng)中兩體相互作用耦合強度的基本參數(shù)。換句話說,我們算法中的能隙Δ與待求解的獨立集問題G(V, E)的大小和結(jié)構(gòu)均無關(guān),這就確保了我們的算法具有一個恒定的運行時間,而且這比解決獨立集問題中態(tài)制備和讀出的時間短很多。(2)驅(qū)動哈密頓量演化只需要局部的幺正操作即可(例如繞固定軸的單比特旋轉(zhuǎn)操作),這大大降低了實驗中對量子系統(tǒng)的操控難度,使得利用可調(diào)線性光學(xué)量子線路來演示非阿貝爾絕熱量子混合算法也是可行的。 量子擴散
所有基態(tài)(對應(yīng)獨立集問題所有解)的相干疊加態(tài)∑an|gn?,最后,我們通過量子投影測量讀出這個波函數(shù)中包含的解的信息,從而解決相應(yīng)的獨立集問題。這便是我們最近實驗工作中用于求解獨立集問題的量子算法的基本演算流程。 我們稱這個與傳統(tǒng)的絕熱演化算法不同的方法為非阿貝爾絕熱量子混合算法[4],在解決獨立集問題上的它具有兩個獨特優(yōu)勢:(1)在絕熱演化過程中,系統(tǒng)基態(tài)和第一激發(fā)態(tài)之間的能隙Δ是一個保持不變的常數(shù)4J,其中J是一個描述系統(tǒng)中兩體相互作用耦合強度的基本參數(shù)。換句話說,我們算法中的能隙Δ與待求解的獨立集問題G(V, E)的大小和結(jié)構(gòu)均無關(guān),這就確保了我們的算法具有一個恒定的運行時間,而且這比解決獨立集問題中態(tài)制備和讀出的時間短很多。(2)驅(qū)動哈密頓量演化只需要局部的幺正操作即可(例如繞固定軸的單比特旋轉(zhuǎn)操作),這大大降低了實驗中對量子系統(tǒng)的操控難度,使得利用可調(diào)線性光學(xué)量子線路來演示非阿貝爾絕熱量子混合算法也是可行的。 量子擴散
從物理圖像上看,非阿貝爾絕熱混合過程可以等效看作一個粒子在高維中值圖中的量子擴散現(xiàn)象[4]。對于一個圖G(V, E),中值圖里的頂點是它的獨立集,當(dāng)且僅當(dāng)兩個獨立集之間的漢明距離(Hamming distance)為一時,兩個頂點之間會有實線相連。為了更明確地闡明這種量子擴散過程,我們以代表性圖G(8, 7)為例,可以看到系統(tǒng)最初被制備在一個簡單的基態(tài)|g0?上,在八維中值圖中我們用中心的黑點來表示(圖6左上圖)。在系統(tǒng)絕熱演化過程中,系統(tǒng)初態(tài)逐漸演化為中間哈密頓量的基態(tài),對應(yīng)于八維中值圖中心的黑點逐漸向四周擴散的過程,同時也是獨立集問題的解開始在希爾伯特空間中自然“涌現(xiàn)”的過程,這里黑點和藍(lán)點分別代表正確的基態(tài),而紅色和空心點代表錯誤的基態(tài)(圖6右圖)。最后,隨著系統(tǒng)哈密頓量重新回到初始時的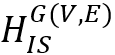 ,系統(tǒng)的基態(tài)最終演化為哈密頓量
,系統(tǒng)的基態(tài)最終演化為哈密頓量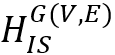 所有基態(tài)的相干疊加,對應(yīng)于八維中值圖中的擴散結(jié)束,所有代表錯誤解的紅點消失,而代表正確解的黑點和藍(lán)點以大致相等的概率分布在八維中值圖中(圖6左下圖)。
所有基態(tài)的相干疊加,對應(yīng)于八維中值圖中的擴散結(jié)束,所有代表錯誤解的紅點消失,而代表正確解的黑點和藍(lán)點以大致相等的概率分布在八維中值圖中(圖6左下圖)。
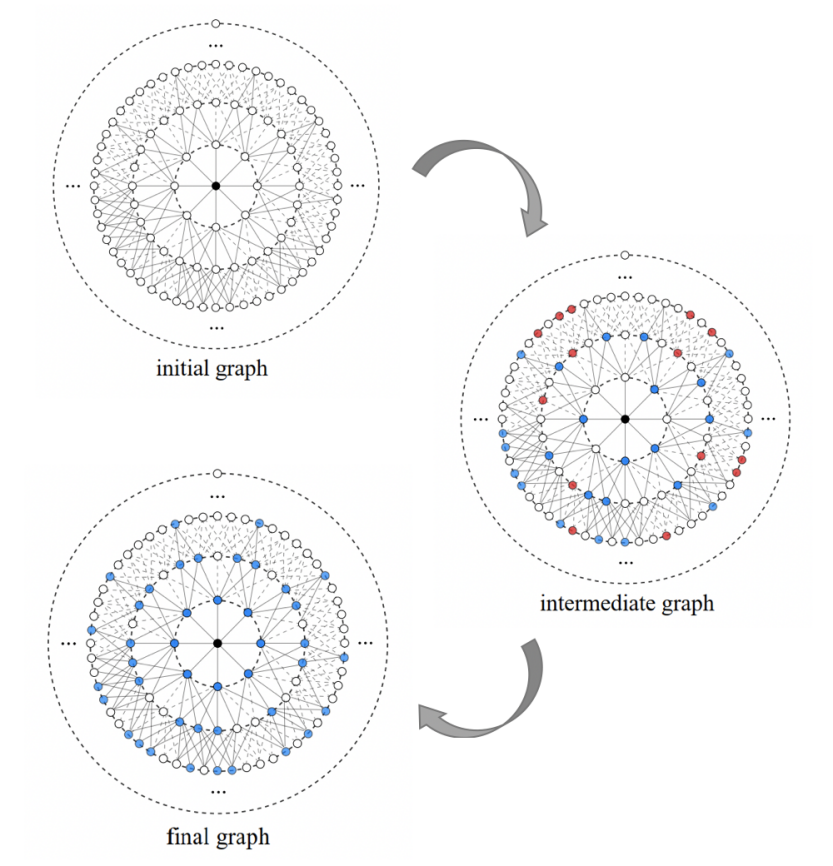
圖6:八維中值圖中的量子擴散過程
基于上述理論模型,中國科大潘建偉、陳宇翱、姚星燦等與北京大學(xué)吳飆、美國麻省理工學(xué)院Frank Wilczek合作,首次在線性光學(xué)量子線路中演示了非阿貝爾絕熱量子混合算法,并成功求解了若干個獨立集問題,其中對圖G(8, 7)的求解成功概率達(dá)到了87.5%,非平庸解占比達(dá)到31.4%。實驗中還觀測到量子態(tài)在高維中值圖空間中的量子擴散過程,為利用非阿貝爾絕熱混合算法解決具有內(nèi)稟非阿貝爾規(guī)范對稱性的組合優(yōu)化問題鋪平了道路,相關(guān)成果最近刊登在了《美國國家科學(xué)院院刊》(PNAS)[5]。
未來,研究者們還會繼續(xù)改進(jìn)現(xiàn)有的絕熱量子算法模型[6],嘗試提高最大獨立集和非平庸獨立集的求解概率,通過降低系統(tǒng)噪聲來壓制得到錯誤解的概率,并進(jìn)一步探索在離子、原子等其他物理系統(tǒng)中實現(xiàn)更大尺度獨立集問題的求解,在NISQ時代為量子計算解決特定復(fù)雜問題提供新的思路和開辟新的道路。
-
二進(jìn)制
+關(guān)注
關(guān)注
2文章
796瀏覽量
41729 -
量子
+關(guān)注
關(guān)注
0文章
480瀏覽量
25534 -
社交網(wǎng)絡(luò)
+關(guān)注
關(guān)注
0文章
48瀏覽量
3839
原文標(biāo)題:量子擴散,讓獨立集問題的解在量子態(tài)空間中自然“涌現(xiàn)”
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導(dǎo)體所】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
【《計算》閱讀體驗】量子計算
什么是“量子自旋霍爾效應(yīng)”?
超導(dǎo)量子芯片有哪些優(yōu)勢?
基于故障樹最小割集求解算法




 量子擴散如何實現(xiàn)更大尺度獨立集問題的求解
量子擴散如何實現(xiàn)更大尺度獨立集問題的求解











評論