了解電子電路（即電阻器和放大器）中的溫度漂移。 我們還將介紹閃爍噪聲的影響如何發揮作用，以及漂移如何限制信號平均的有效性。

即使在固定的電氣條件（電源電壓、輸入和負載）下，電子電路也不會完全穩定，因為它們往往會隨時間和溫度漂移。 這些與理想行為的偏差會給精密測量增加相當大的誤差。 為了深入了解電子產品的溫度漂移，本文簡要介紹了電阻和放大器的溫度行為。 我們還將討論閃爍噪聲的影響可能不容易與輸出中溫度引起的漂移區分開來。 最后，我們將討論漂移會限制
信號平均技術 通常用于提高可重復測量的準確性。

電阻溫度漂移—電阻溫度系數

作為最簡單的電子元件類型，電阻器作為高性能電路中的誤差源可能會被忽視。 但是，電阻器的值不是恒定的，并且隨溫度和時間而變化。 例如，如果電阻的溫度系數為±50
ppm/°C，環境溫度比參考溫度（室溫）高100°C，則電阻的值可以變化±0.5%。

幸運的是，在許多應用中，電路精度由兩個或多個電阻的比值決定，而不是單個電阻的絕對值。 在這些情況下，匹配的電阻網絡，例如
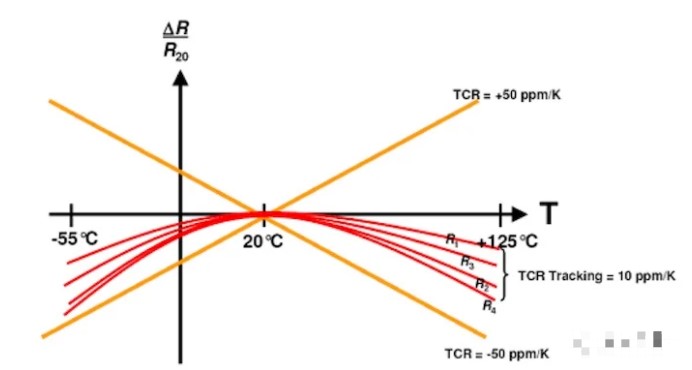
LT5400，可以使用。 電阻形成一個共基板網絡，并表現出良好匹配的溫度行為。 圖1比較了單個分立電阻與匹配電阻網絡的溫度行為。

*圖1. 匹配電阻網絡溫度行為的分立電阻。 圖片由 維沙伊

在此圖中，橙色線表示單個±50 ppm/°C電阻值的變化限值，因為溫度從參考溫度（20°C）沿任一方向變化。 紅色曲線對應于來自匹配電阻網絡的四個電阻，它們表現出相似的溫度行為。 匹配電阻的溫度系數 （TC） 相互跟蹤，通常在 2–10 ppm/°C 以內。 具有良好匹配溫度行為的電阻器可能是某些精密應用的基本要求，例如 電阻電流檢測.

具有相同溫度系數的溫度感應漂移

應該注意的是，即使TC值相同，電路中的電阻也會產生與溫度相關的漂移。 下面可以看到圖 2 中的示例。

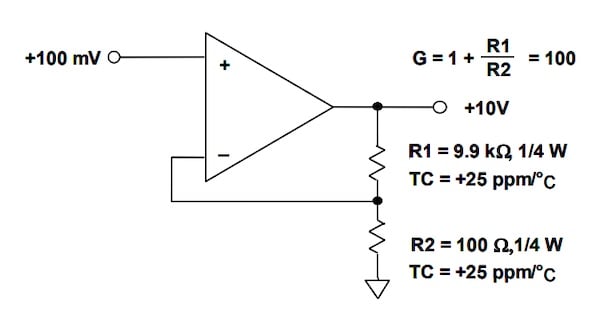
*圖2. 產生溫度相關漂移的示例。 **圖片 [修改] 使用由 ADI公司]

在上圖中，兩個電阻具有相同的TC（+25 ppm/°C）; 然而，電阻兩端的電壓以及兩個電阻的功耗非常不同。 R兩端的電壓2 = 100 Ω為0.1 V，功耗為0.1 mW。 然而，電壓兩端的電壓R.1 為 9.9 V; 因此，該電阻兩端的功耗為9.9 mW。 假設 熱阻兩個電阻均為125°C/W，溫度為R1 和 R2 將分別比環境溫度升高1.24°C和0.0125°C。 這種不相等的自熱效應導致兩個電阻漂移不同的量。

圖3（a）顯示了另一個示例，其中相同的TC不一定能解決溫度漂移問題。

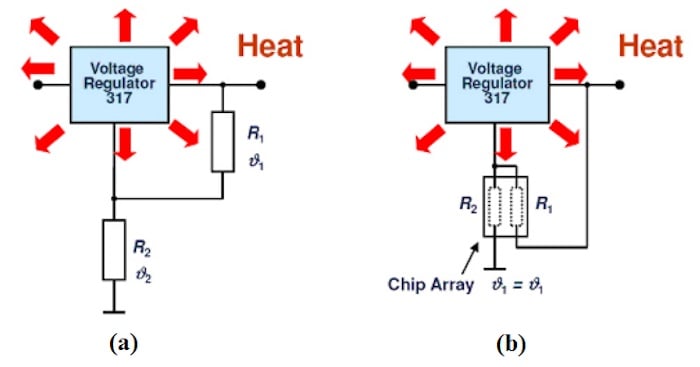
圖3. 使用（a）分立電阻器表示不同本地環境溫度的示例，以及（b）使用集成電阻器/電阻器陣列表示相同的局部環境溫度的示例。 *圖片由 維沙伊

在上圖中，如果設計包含不相等電阻（R1 ≠· 2 ），在相同的TC下，電阻的自發熱會產生溫度引起的漂移，如上所述。 但是，穩壓器可能會引起額外的溫度梯度。 即使兩個電阻的電阻和TC相同（R1 = R2 和 TC1 = TC 2 ).

可以使用電阻陣列來避免上述示例的漂移問題（圖 3（b））。 在單個基板上實現電阻網絡時，兩個電阻器熱耦合并經歷相同的環境溫度。

其他電路中的溫度漂移—運算放大器溫度漂移

由于簡單的電阻容易受到溫度和老化的影響，因此其他更復雜的電路的參數也隨溫度和時間漂移也就不足為奇了。 例如，放大器的輸入失調電壓隨溫度和時間而變化。 這會產生時變誤差，限制可測量的最小直流信號。 典型通用精密運算放大器的失調漂移范圍為1–10
μV/°C。

如果放大器的失調漂移限制了測量精度，我們可以考慮使用斬波穩定放大器。 這些器件使用失調消除技術將失調電壓降低到非常低的水平（例如，小于10
μV），并產生接近零漂移的操作。 斬波穩定放大器的失調漂移，例如 來自微芯片的MCP6V51，可低至 36 nV/°C。

溫度漂移或閃爍噪聲（1/f）？

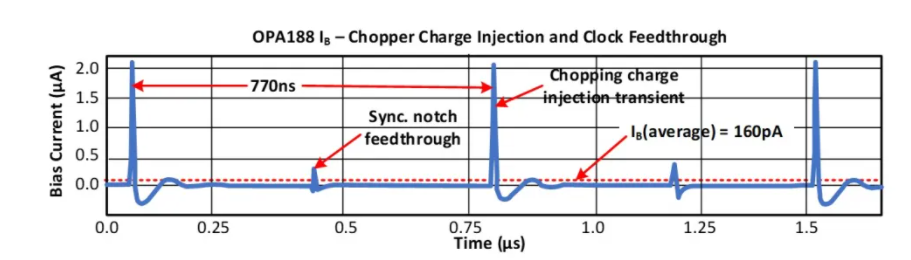
在非常低的頻率下，閃爍噪聲是影響電路輸出的主要噪聲源。 閃爍噪聲的平均功率與工作頻率成反比（這就是為什么閃爍噪聲也稱為1/f噪聲）。 頻率越低，1/f噪聲的平均功率越高。 如果我們測量電路的輸出足夠長的時間，我們可以捕獲這種低頻噪聲的影響。 圖4顯示了閃爍噪聲在輸出端產生的放動
ADA4622-2.

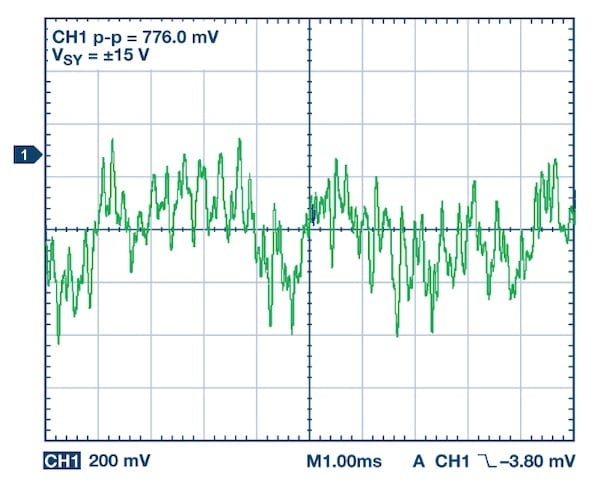
*圖4. ADA4622-2輸出閃爍噪聲的放動。圖片由 ADI公司

ADA4622-2是一款精密運算放大器，0.1 Hz至10 Hz噪聲典型值為0.75 μV p-p。 上圖的波形顯示了ADA4622-2的0.1 Hz至10 Hz噪聲放大后為1000倍。 如您所見，閃爍噪聲會導致輸出隨機緩慢波動。 這些波動是由不同于溫度或老化引起的漂移的現象產生的。 然而，由于其低頻特性，1/f噪聲的影響可能不容易與信號漂移區分開來。

對于運算放大器，失調漂移和1/f噪聲都會在輸出端引起緩慢誤差。 這就是為什么使用失調消除技術來降低失調漂移的零漂移運算放大器在輸出端沒有1/f噪聲的原因。 圖5比較了連續時間放大器與零漂移放大器的1/f噪聲。

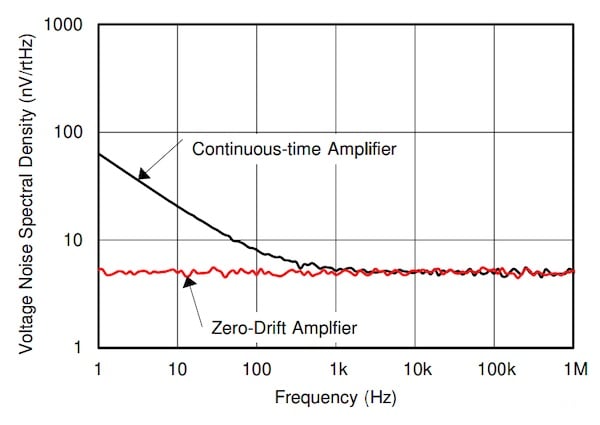
*圖5. 連續時間放大器與零漂移放大器的噪聲。 圖片由 鈦

漂移會限制信號平均的有效性嗎？

另一種有效的降噪技術是信號平均。 如果我們有一個噪聲方差為 σ_n^2的可重復實驗，我們可以重復實驗 M 次并平均相應的輸出樣本，以將噪聲方差減小為：s2nσn2，我們可以重復實驗M次，并對相應的輸出樣本求平均值，將噪聲方差降低到：

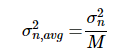
等式 1.

其中 $$
σ_{n， avg}^2

表示平均信號的噪聲方差。盡管信號平均在某些應用中有效，但它仍然有其局限性。信號平均基于噪聲樣本彼此不相關的假設。測量數據中的緩慢漂移可能充當低頻相關噪聲分量，并限制信號平均技術的有效性。在這種情況下，噪聲抑制將低于公式1預測的噪聲抑制。s2n,一個在gsn,一個在g2 表示平均信號的噪聲方差。盡管信號平均在某些應用中有效，但它仍然有其局限性。信號平均基于噪聲樣本彼此不相關的假設。測量數據中的緩慢漂移可能充當低頻相關噪聲分量，并限制信號平均技術的有效性。在這種情況下，噪聲抑制將低于公式1預測的噪聲抑制。 此外，根據給定應用中隨機漂移的類型，平均信號的方差可能會增加到超過某些M值以上。在另一篇文章中，我們將更仔細地研究信號平均技術的這種局限性，并介紹一個有用的統計分析工具，稱為 艾倫方差，這使我們能夠更深入地了解電路的輸出如何由于閃爍噪聲、溫度效應等不同現象而趨向漂移。