本文解決的問題:
機械手搭載雙目相機,手眼標定。
本文有細致的推導過程,非常全面。
什么是手眼標定
確定像素坐標系和空間機械手坐標系的坐標轉化關系;
為什么會存在這個?
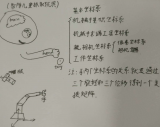
舉一個生活中常見的例子——用手移動物體:
第一步:眼睛觀察到三維世界,并將其轉換到視網膜平面(三維空間轉換到二維平面)傳送信息給大腦;
第二步:大腦想要移動某個物體,假設想要將物體從A點移動B點(二維坐標),但是物體是三維空間中的物體,是三維坐標,需要將二維坐標換算成三維坐標;
第三步:大腦已經獲得A點和B點的三維坐標,大腦給手(執行機構)發出指令去完成這個任務;
其中第二步就是手眼標定,得到二維坐標(像素坐標)到三維坐標的轉換矩陣
在實際控制中,相機檢測到目標在圖像中的像素位置后,通過標定好的坐標轉換矩陣將相機的像素坐標變換到機械手的空間坐標系中,然后根據機械手坐標系計算出各個電機該如何運動,從而控制機械手到達指定位置。這個過程中涉及到了圖像標定,圖像處理,運動學正逆解,手眼標定等。
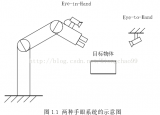
相機的裝載位置
不在手上(eye-to-hand)
相機固定在一個地方,機械手的運動不會帶著相機一起移動。
在手上(eye-in-hand)
相機安裝在機械手上,隨著機械手一起移動。較為常用。這個實際上和eye-to-hand類似。
可以快速有效地標定被測物體的坐標。
這種情況的標定過程實際上和相機和機械手分離的標定方法是一樣的,因為相機拍照時,機械手會運動到相機標定的時候的位置,然后相機拍照,得到目標的坐標,再控制機械手,所以簡單的相機固定在末端的手眼系統很多都是采用這種方法,標定的過程和手眼分離系統的標定是可以相同對待的。
●基于圖像的視覺控制
●基于位置的視覺控制
●結合兩者的混合視覺控制
在正式開始講解之前,可以看一下:深入淺出地理解機器人手眼標定
對手眼標定有一個直觀的認識。
正式開始
本文的相機搭載方案是,hand-in-eye。移動相機,標定求解過程
在推導過程中,我們會用到四個坐標系,分別是:
●基礎坐標系(用base表示)
●機械手坐標系(用tool表示)
●相機坐標系(用cam表示)
●標定物坐標系(用cal表示)
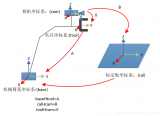
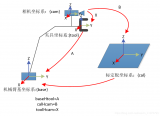
下面先給出示意圖:
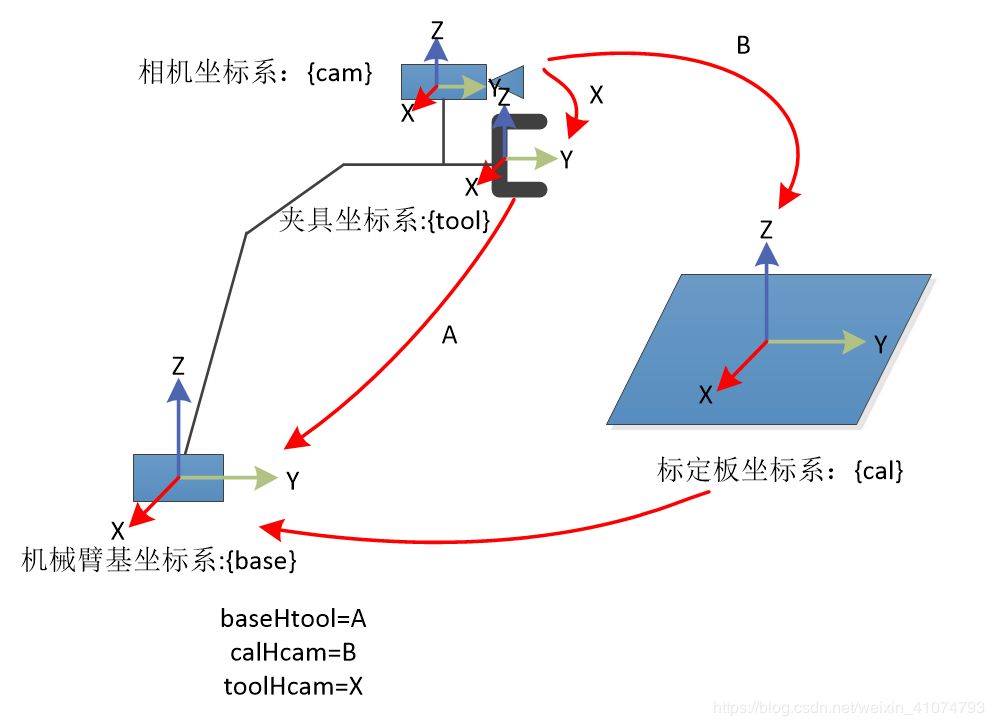
坐標系之間的轉換關系說明:
●baseHtool:表示機械手坐標系到基礎坐標系的轉換關系,可以由機器人系統中得出。(已知)
●toolHcam:表示相機坐標系到機械手坐標系的轉換關系;這個轉化關系在機械手移動過程中是不變的;(未知,待求)
●calHcam:表示相機坐標系到標定板坐標系的轉換關系(相機外參),可以由相機標定求出;(相當于已知)
●baseHcal:表示標定板坐標系到基礎坐標系的變換,這個是最終想要得到的結果;只要機械手和標定板的相對位置不變,這個變換矩陣不發生變化。

所以:其中的A已知,X待求,B需要通過相機標定得知(張正友標定法可以求得)。
驗證結果

1. 基礎坐標系(求解baseHtool)
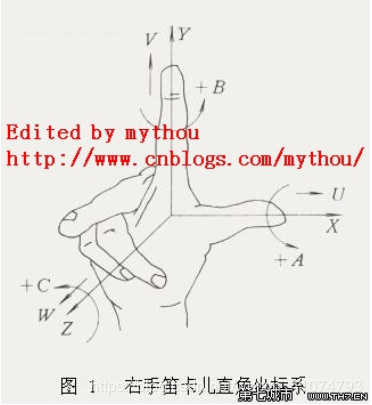
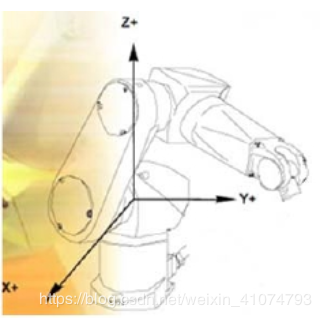
符合右手定則的XYZ三個坐標軸
●原點:機器人底座的中心點
●X軸正向:指向機器人的正前方
●Z軸正向:指向機器人的正上方
●Y軸正向:由右手定則確定
六個自由度
●三個位置:x、y、z(第六軸法蘭盤圓心相對于原點的偏移量)
●三個角:Rx、Ry、Rz(第六軸法蘭盤的軸線角度,由初始姿態即豎直向上繞x軸旋轉Rx度,再繞Y軸旋轉Ry度,再繞Z軸旋轉Rz度得到)
●旋轉方式(機器人RPY角和Euler角 – 基本公式)(機器人學-熊有倫36-40頁)
●繞定軸X-Y-Z旋轉(判斷機械臂輸出四元數與代碼得到的四元數是否相等得到)

一定要注意歐拉角和李代數不一樣,非常容易搞混,因為他們都是3個量
歐拉角:分別繞x、y、z軸旋轉的角度,不一樣的旋轉次序,得到的R不一樣;
李代數:維度是3,是繞一個軸轉動一定的角度。歐拉角可以理解成李代數在x、y、z軸上的分解旋轉。(不一定正確,不過比較形象)
注:不同機械臂示教器顯示的法蘭盤的數據格式不一樣,有的是用歐拉角顯示的,有的是用角軸顯示的。
2. camHcal相機到標定板
●注意:標定板坐標系下的坐標轉換到相機坐標系下
思路大致如下:
●已知雙目相機的內參、畸變系數、外參(Pr=R?Pl+t P_r=R*P_l+tP
r=R?P l +t),
●對左右相機的兩張圖片調用OpenCV中的findChessboardCorners函數,找到內角點(如果結果不好,繼續提取亞像素點);
●將左右相機的像素點對應起來,得到匹配的2d點;
●使用空間異面直線的方法,用對應的2d點計算出以右相機為世界坐標系的3維坐標Pcam P_{cam}P cam ;(立體視覺匹配)
●計算出每個角點以棋盤格為世界坐標的3維坐標Pcal P_{cal}P cal;
●通過解方程Pcam=camHcal?Pcal P_{cam}=camHcal*P_{cal}P cam=camHcal?P cal 求解出外參(3d-3d:ICP,SVD奇異值分解(十四講173頁))
張正友相機標定Opencv實現

參數解釋:
●第一個參數Image,傳入拍攝的棋盤圖Mat圖像,必須是8位的灰度或者彩色圖像;
●第二個參數patternSize,每個棋盤圖上內角點的行列數,一般情況下,行列數不要相同,便于后續標定程序識別標定板的方向;
●第三個參數corners,用于存儲檢測到的內角點圖像坐標位置,一般用元素是Point2f的向量來表示:vector image_points_buf;
●第四個參數flage:用于定義棋盤圖上內角點查找的不同處理方式,有默認值。
3. 求解AX=XB
以下四篇論文對應著四種求解方法
Tsai, Roger Y., and Reimar K. Lenz. “A new technique for fully autonomous and efficient 3D robotics hand/eye calibration.” IEEE Transactions on robotics and automation 5.3 (1989): 345-358.(博客:Tsai-Lenz的OpenCV實現)
Horaud, Radu, and Fadi Dornaika. “Hand-eye calibration.” The international journal of robotics research 14.3 (1995): 195-210.
Park, Frank C., and Bryan J. Martin. “Robot sensor calibration: solving AX= XB on the Euclidean group.” IEEE Transactions on Robotics and Automation10.5 (1994): 717-721.(博客:Navy的OpenCV實現)
Daniilidis, Konstantinos. “Hand-eye calibration using dual quaternions.” The International Journal of Robotics Research 18.3 (1999): 286-298.
文獻3采用的是李群的理論,將AX=XB轉化成最小二乘問題;
文獻4采用的時對偶四元數的知識,用對偶四元數表達旋轉和平移,從而進行統一計算;
著四種算法精度差不多,不過文獻4的效果要更好點。
具體實現文獻3的算法,下面具體介紹
對數:乘法變加法
李群李代數

利用李群知識求解AX=XB

采用“兩步法”求解上述方程,先解算旋轉矩陣,再求得平移向量。
求解旋轉矩陣



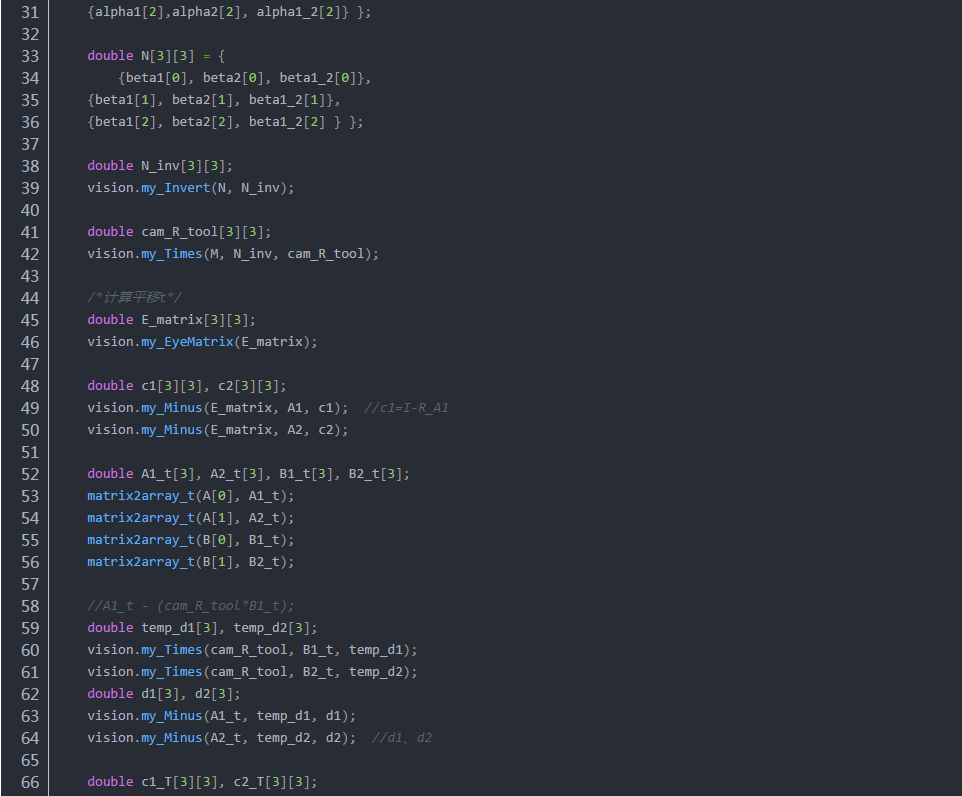
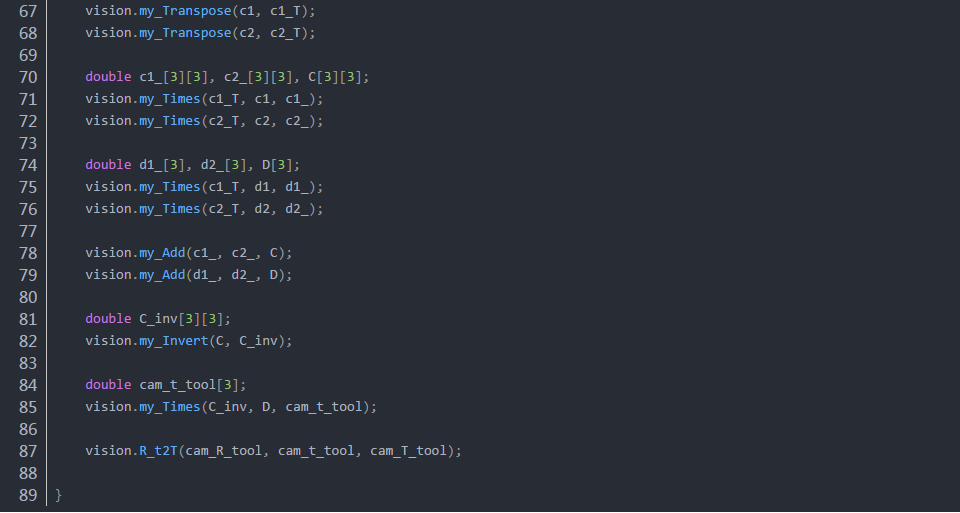
代碼:用兩組數據求解方程AX=XB
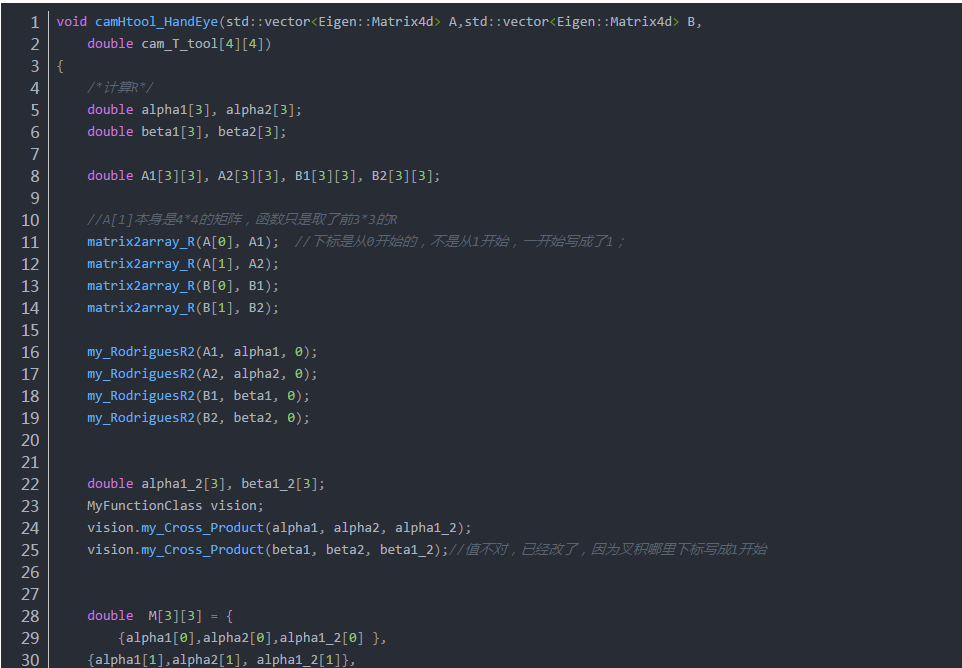
審核編輯:湯梓紅
-
機器人
+關注
關注
211文章
28502瀏覽量
207485 -
相機
+關注
關注
4文章
1358瀏覽量
53705 -
坐標系
+關注
關注
0文章
29瀏覽量
7339 -
機械手
+關注
關注
7文章
336瀏覽量
29680 -
視覺控制
+關注
關注
0文章
8瀏覽量
6873
原文標題:【光電智造】手眼標定—全面細致的推導過程
文章出處:【微信號:今日光電,微信公眾號:今日光電】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Realsense+大象機器人手眼標定方案詳解

詳解機器人手眼標定MATLAB及C++實現
請問各位高手,如何用labview的vision實現手眼標定
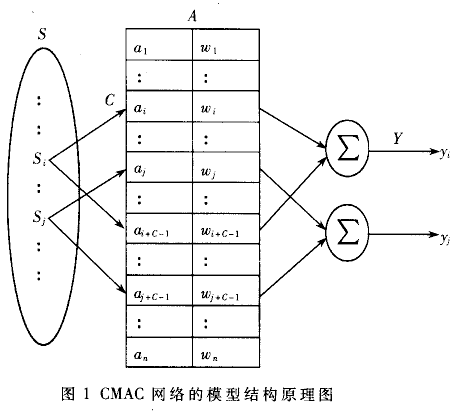
CMAC網絡在機器人手眼系統位置控制中的應用
凸松弛全局優化機器人手眼標定

手眼標定_全面細致的推導過程
常見的機器人視覺伺服中的標定技術有哪些




 機器人手眼標定的推導過程
機器人手眼標定的推導過程











評論