標(biāo)定技術(shù)

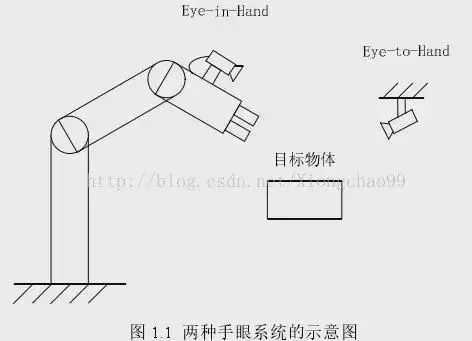
常見(jiàn)的機(jī)器人視覺(jué)伺服中要實(shí)現(xiàn)像素坐標(biāo)與實(shí)際坐標(biāo)的轉(zhuǎn)換，首先就要進(jìn)行標(biāo)定，對(duì)于實(shí)現(xiàn)視覺(jué)伺服控制，這里的標(biāo)定不僅包括攝像機(jī)標(biāo)定，也包括機(jī)器人系統(tǒng)的手眼標(biāo)定。以常見(jiàn)的焊接機(jī)器人系統(tǒng)為例，有兩種構(gòu)型，如下：

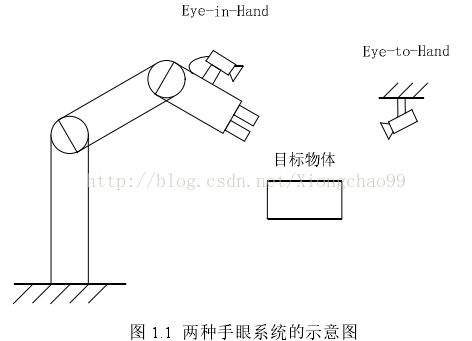
即：攝像機(jī)固定于機(jī)器手和攝像機(jī)固定于外部場(chǎng)景；

本文針對(duì)前一種構(gòu)型：攝像機(jī)固定于機(jī)器手。

1、攝像機(jī)標(biāo)定技術(shù)

（1）理論部分：

以張正友的棋盤(pán)標(biāo)定法為攝像機(jī)標(biāo)定方式，由于攝像機(jī)標(biāo)定結(jié)果要用到后面的手眼標(biāo)定中，所以此處進(jìn)行不同方位的棋盤(pán)圖片拍攝時(shí)需要遵守：標(biāo)定板固定位置不動(dòng)，手眼組合體變換姿態(tài)拍攝圖片。

攝像機(jī)標(biāo)定的目的：得到兩組坐標(biāo)系的兩兩轉(zhuǎn)化矩陣：T1和T2；

1）得到圖片像素坐標(biāo)系P與攝像機(jī)坐標(biāo)系C之間的轉(zhuǎn)換矩陣T1，準(zhǔn)確說(shuō)應(yīng)該是攝像機(jī)坐標(biāo)系轉(zhuǎn)化為圖片像素坐標(biāo)系的轉(zhuǎn)換矩陣。可表示為：

P=T1*C;

解釋：T1在攝像機(jī)標(biāo)定結(jié)果中就是內(nèi)參矩陣3x3；

2）得到攝像相機(jī)坐標(biāo)系C與棋盤(pán)上建立的世界坐標(biāo)系G之間的轉(zhuǎn)換矩陣T2，準(zhǔn)確說(shuō)應(yīng)該是坐標(biāo)系G轉(zhuǎn)化為攝像機(jī)坐標(biāo)系的轉(zhuǎn)換矩陣。可表示為：

C=T2*G;

解釋：T2在攝像機(jī)標(biāo)定結(jié)果中就是外參矩陣4x4，由旋轉(zhuǎn)矩陣r和平移向量t構(gòu)成[ t ?r; 0 0 0 1]；

（2）方法：

攝像機(jī)標(biāo)定方法有兩種可選：openCV或者Matlab標(biāo)定工具箱；

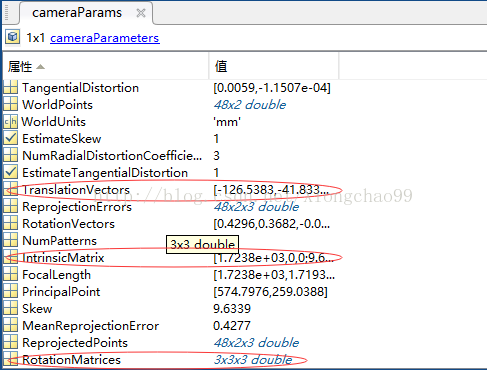
建議選擇MATLAB應(yīng)用程序——圖像處理與計(jì)算機(jī)視覺(jué)——Camera Calibrator，直接導(dǎo)入拍攝好的圖片即可。但是要注意，使用matlab標(biāo)定工具箱所得到的內(nèi)參矩陣、外參旋轉(zhuǎn)矩陣、外參平移向量都要經(jīng)過(guò)轉(zhuǎn)置才是正確的結(jié)果。

如下圖，MATLAB標(biāo)定得到的紅框中依次是外參平移向量、內(nèi)參矩陣、外參旋轉(zhuǎn)矩陣，它們都需要做轉(zhuǎn)置后才能應(yīng)用于本文的公式計(jì)算：

2、手眼標(biāo)定技術(shù)

（1）理論部分：

手眼標(biāo)定目的：得到攝像機(jī)坐標(biāo)系C與機(jī)器手（或工具）坐標(biāo)系H之間的轉(zhuǎn)換矩陣T3，準(zhǔn)確說(shuō)應(yīng)該是機(jī)器手坐標(biāo)系轉(zhuǎn)化為攝像機(jī)坐標(biāo)系的轉(zhuǎn)化矩陣。可表示為：

C=T3*H;

解釋：T3需要根據(jù)公式CX=XD得到；實(shí)際中，分別知道C、D求出來(lái)的X有無(wú)窮多個(gè)解。所以為了實(shí)現(xiàn)唯一解，我們至少需要兩組C和D，即至少需要3個(gè)位置的攝像機(jī)標(biāo)定結(jié)果。

其中C的求法如下：

C是兩個(gè)攝像機(jī)坐標(biāo)系之間的變換矩陣。可以根據(jù)上述任一兩張標(biāo)定圖片所得的兩個(gè)攝像機(jī)標(biāo)定外參A、B按公式C=A*inv(B)計(jì)算得到的。假設(shè)上述攝像機(jī)標(biāo)定中有3張標(biāo)定圖片的外參標(biāo)定結(jié)果分別是T21、T22、T23，那么可以得到兩個(gè)C矩陣：

C1=T21*inv(T22);

C2=T22*inv(T23);

D的求法如下：

D是兩個(gè)機(jī)器手坐標(biāo)系之間的變換矩陣。假設(shè)上述攝像機(jī)標(biāo)定中的3張標(biāo)定圖片所一一對(duì)應(yīng)的機(jī)器手坐標(biāo)系在基坐標(biāo)系（也可以是工件坐標(biāo)系或者其他固定的參考坐標(biāo)系）中的描述矩陣結(jié)果分別是H1、H2、H3（H需要從機(jī)器人控制器或示教器中讀取），那么可以得到兩個(gè)D矩陣：

D1=inv(H1)*H2;

D2=inv(H2)*H3;

由以上兩組C和D，代入CX=XD就可以得到唯一解X，從而T3=X；

注：上述H1、H2、H3是每張標(biāo)定圖片對(duì)應(yīng)的機(jī)器手坐標(biāo)系描述矩陣，正好說(shuō)明了攝像機(jī)標(biāo)定中所謂的“標(biāo)定板固定，手眼運(yùn)動(dòng)”的正確性。如果手眼不動(dòng)，改變標(biāo)定板姿態(tài)進(jìn)行拍攝，那么H的值都是一樣的。

（2）方法：

1）根據(jù)攝像機(jī)標(biāo)定已知攝像機(jī)外參矩陣T21、T22、T23，還要從機(jī)器人控制器中讀取T21、T22、T23分別對(duì)應(yīng)的機(jī)器手(或工具)坐標(biāo)系H1、H2、H3。控制器中的坐標(biāo)系描述矩陣不是直接讀取的，它是以平移向量和歐拉角（或四元數(shù)）模式存在的，如下：

平移向量+歐拉角模式：

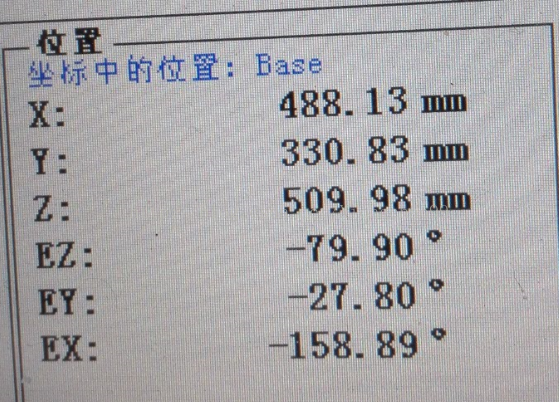
平移向量+四元數(shù)模式：

選取其中任一模式即可，然后將其轉(zhuǎn)化為描述矩陣。

上述工作完成后，就已經(jīng)獲取了3個(gè)外參矩陣（再次提醒，攝像機(jī)標(biāo)定使用MATLAB標(biāo)定工具箱的話，所得到的外參旋轉(zhuǎn)矩陣和平移向量先要轉(zhuǎn)置，即R=r'，T=t'，然后外參矩陣EX=[R T；0 0 0 1]）和 3個(gè)機(jī)械手坐標(biāo)系矩陣，因此可以分別將3個(gè)二維矩陣合為一個(gè)三維矩陣，matlab命令如下：

C_ext=cat(3, C_ext1,?C_ext2,?C_ext3);

H=cat(3, H1, H2 ,H3)

最后將C_ext和H作為參數(shù)代入到如下MATLAB函數(shù)中：

function Tch = GetCamera2HandMatrix(C_ext,H)
%   以下變量：
%   C_ext是3個(gè)位置的攝像機(jī)外參矩陣：3x4x4
%   H1、H2、H3分別是3個(gè)位置的機(jī)械手坐標(biāo)系的姿態(tài)矩陣：3x4x4
%   Tcg--機(jī)器手坐標(biāo)系（或工具坐標(biāo)系）在攝像機(jī)坐標(biāo)系中的姿態(tài)和位置變換矩陣

%   C1、D1、C2、D2、R、w、q、kc1、kc2、kc3、kd1、kd2、kd3、a、b、c、d、h、y均為臨時(shí)變量

    C1=C_ext(:,:,1)*inv(C_ext(:,:,2))
    C2=C_ext(:,:,2)*inv(C_ext(:,:,3))
    D1=inv(H(:,:,1))*H(:,:,2)
    D2=inv(H(:,:,2))*H(:,:,3)
    
    R=C1(1:3,1:3);
    q=acos((trace(R)-1)/2);
    w(1,1)=q/(2*sin(q))*(R(3,2)-R(2,3));
    w(2,1)=q/(2*sin(q))*(R(1,3)-R(3,1));
    w(3,1)=q/(2*sin(q))*(R(2,1)-R(1,2));
    kc1=w;
    
    R=C2(1:3,1:3);
    q=acos((trace(R)-1)/2);
    w(1,1)=q/(2*sin(q))*(R(3,2)-R(2,3));
    w(2,1)=q/(2*sin(q))*(R(1,3)-R(3,1));
    w(3,1)=q/(2*sin(q))*(R(2,1)-R(1,2));
    kc2=w;
    
    R=D1(1:3,1:3);
    q=acos((trace(R)-1)/2);
    w(1,1)=q/(2*sin(q))*(R(3,2)-R(2,3));
    w(2,1)=q/(2*sin(q))*(R(1,3)-R(3,1));
    w(3,1)=q/(2*sin(q))*(R(2,1)-R(1,2));
    kd1=w;
    
    R=D2(1:3,1:3);
    q=acos((trace(R)-1)/2);
    w(1,1)=q/(2*sin(q))*(R(3,2)-R(2,3));
    w(2,1)=q/(2*sin(q))*(R(1,3)-R(3,1));
    w(3,1)=q/(2*sin(q))*(R(2,1)-R(1,2));
    kd2=w;
    
    kc3=cross(kc1,kc2);
    kd3=cross(kd1,kd2);
    a=[kc1 kc2 kc3];
    b=[kd1 kd2 kd3];
    R=a*inv(b);  %得到旋轉(zhuǎn)關(guān)系矩陣
    
    tc1=C1(1:3,4);
    tc2=C2(1:3,4);
    td1=D1(1:3,4);
    td2=D2(1:3,4);
    c=R*td1-tc1;
    d=R*td2-tc2;
    a=C1(1:3,1:3)-[1 0 0;0 1 0;0 0 1];
    b=C2(1:3,1:3)-[1 0 0;0 1 0;0 0 1];
    h=[a;b];
    y=[c;d];
    t=inv(h'*h)*h'*y;   %得到平移關(guān)系矩陣
    
    Tch=[R t;0 0 0 1];   %得到最終結(jié)果
end

3、根據(jù)標(biāo)定結(jié)果對(duì)固定高度目標(biāo)實(shí)現(xiàn)單目定位

（1）理論部分：

由上述1、2兩個(gè)標(biāo)定已經(jīng)得到：

攝像機(jī)坐標(biāo)系C->像素坐標(biāo)系P的轉(zhuǎn)換矩陣Tpc（即內(nèi)參矩陣，MATLAB標(biāo)定得到的要轉(zhuǎn)置）；

機(jī)械手（或工具）坐標(biāo)系H->攝像機(jī)坐標(biāo)系C的轉(zhuǎn)化矩陣Tch；

從控制器讀取的機(jī)械手（或工具）坐標(biāo)系H->基坐標(biāo)系B（這個(gè)根據(jù)情況自己在控制器設(shè)定是基坐標(biāo)還是工件坐標(biāo)系，本文用基坐標(biāo)系）的轉(zhuǎn)化矩陣Tbh；

已知目標(biāo)高度固定，為z；

那么基坐標(biāo)系轉(zhuǎn)化為像素坐標(biāo)系的變換矩陣就是：Gpb=Tpc*Tch*inv(Tbh);

根據(jù)Gpb和z可以得到如下圖所示的變換過(guò)程，分解后可根據(jù)像素坐標(biāo)(u,v)求得實(shí)際坐標(biāo)(x,y,z)：

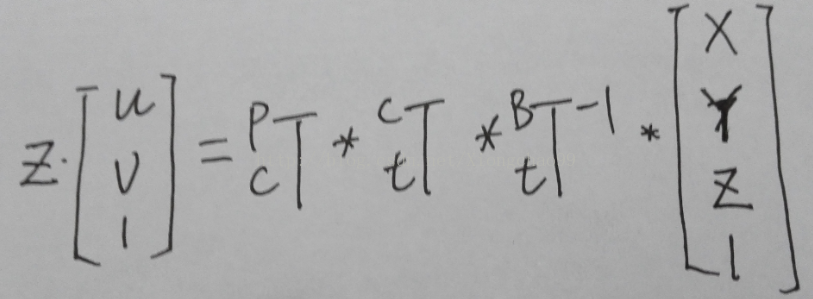
其中，Tpc需要注意，應(yīng)在內(nèi)參矩陣最后添加一個(gè)全零列，變?yōu)?x4矩陣，如下：

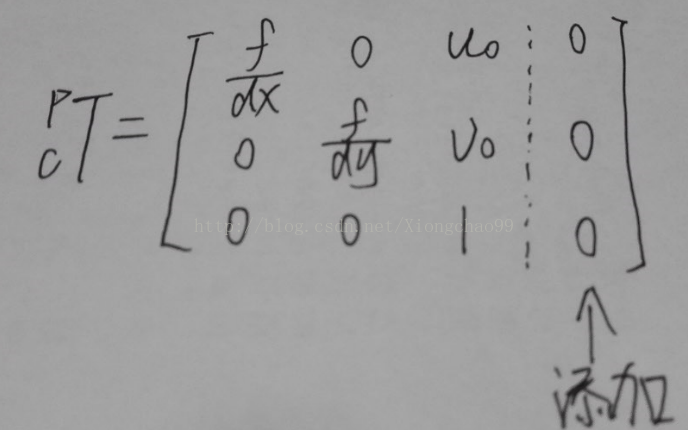
（2）代碼實(shí)現(xiàn)：

function  P= GetObjectLocation( u,v,Gtb)
%   參數(shù)(u,v)為目標(biāo)在圖片中的像素坐標(biāo)
%   參數(shù)Gtb是工具在機(jī)器人基坐標(biāo)中的描述矩陣（也就是工具坐標(biāo)系->基坐標(biāo)系的變換矩陣）

    %內(nèi)參矩陣
    Kl=[ 1851    9.7    550.5  0;
         0    1844.4    299.7  0;
         0         0    1.0    0];
    %攝像機(jī)與工具關(guān)系矩陣
    Gctl= [-0.9620   -0.2974    0.0156   -2.6405;
    0.3266   -0.9552    0.0056   59.7141;
    0.0130    0.0003    1.0161  145.3381;
         0         0         0    1.0000];

    G=inv(Gtb);
    z=10;  %指定物體的高度
    M=Kl*Gctl*G;
    Ml=[u*M(3,1)-M(1,1)  u*M(3,2)-M(1,2)  ;   v*M(3,1)-M(2,1)  v*M(3,2)-M(2,2)];
    Mr=[M(1,4)-u*M(3,4)-(u*M(3,3)-M(1,3))*z;  M(2,4)-v*M(3,4)-(v*M(3,3)-M(2,3))*z];
    P=inv(Ml)*Mr;  %得到物體的位置
end

編輯：黃飛

?