正文
自麥克斯韋方程建立以來,求解已知激勵(lì)、特定邊界條件下的麥克斯韋方程組的解一直是一百多年以來最受關(guān)注的問題之一。
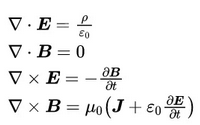
圍繞著麥克斯韋方程組的求解,無數(shù)科研工作者前赴后繼的努力,才有了計(jì)算電磁學(xué)如今的面貌,發(fā)展過程大致可以分為四個(gè)階段:
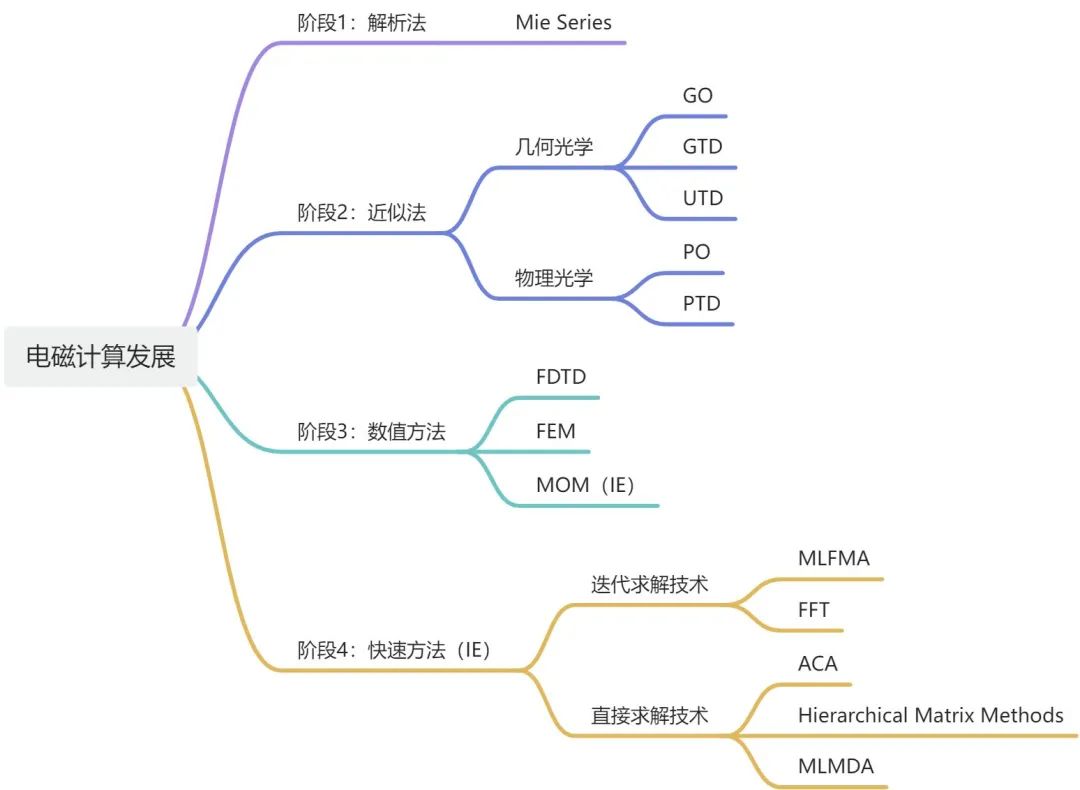
階段1:解析法
對(duì)于結(jié)構(gòu)形式簡(jiǎn)單的模型,依托高超的數(shù)學(xué)技能,基于maxwell方程和邊界條件,可以計(jì)算出空間場(chǎng)分布,即解析解。其優(yōu)點(diǎn)在于:結(jié)果為嚴(yán)格得數(shù)學(xué)推導(dǎo),結(jié)果完全正確,沒有誤差,因而可以作為標(biāo)準(zhǔn)去驗(yàn)證各種計(jì)算方法得正確性,也常作為RCS測(cè)試中定標(biāo)體,對(duì)測(cè)試系統(tǒng)進(jìn)行標(biāo)定。
1908年,Gustav Mie 給出了均勻圓球?qū)ζ矫娌ㄉ⑸涞脟?yán)格解(Mie理論)。具體理論推導(dǎo)可以參考江長(zhǎng)蔭于1996年發(fā)表在《電波科學(xué)學(xué)報(bào)》上得論文。

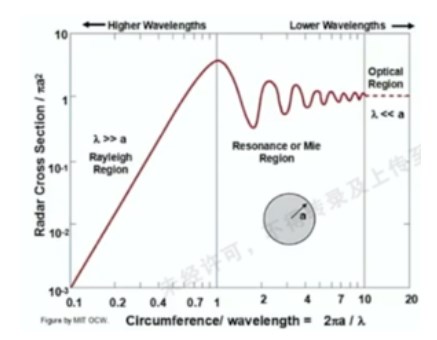
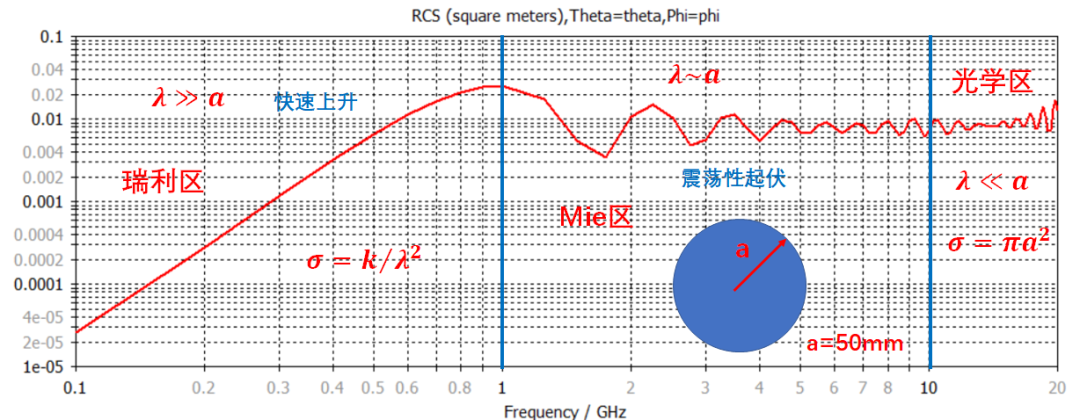
使用CST仿真軟件的時(shí)域求解器(Transistor),對(duì)球的寬帶單站RCS進(jìn)行了計(jì)算:取球半徑為50mm,計(jì)算頻率為0.1GHz~20GHz,參考文獻(xiàn)對(duì)求解結(jié)果的分區(qū):
1)0.1GHz~1GHz頻段內(nèi),波長(zhǎng)遠(yuǎn)大于球半徑,為瑞利區(qū),此時(shí)單站RCS 隨頻率升高而快速變大;
2)1GHz~10GHz頻段內(nèi),波長(zhǎng)與半徑相當(dāng),為Mie區(qū),單站RCS隨頻率升高呈現(xiàn)震蕩性起伏;
3)10GHz~infinity,波長(zhǎng)遠(yuǎn)小于半徑,為光學(xué)區(qū),單站RCS隨頻率變化呈現(xiàn)基本穩(wěn)定。
使用FEKO仿真軟件對(duì)單頻點(diǎn)(10GHz)處金屬球的雙站RCS進(jìn)行了計(jì)算,其雙站RCS的分布形式與往期文章中介紹的陣列天線的方向圖有些相似,與感性的認(rèn)知不同,其最大散射方向并不是后向,而是前向,即與入射電磁波同向。這是不是就是科幻小說《三體》中,使用太陽作為無線電放大器的理論依據(jù),哈哈。
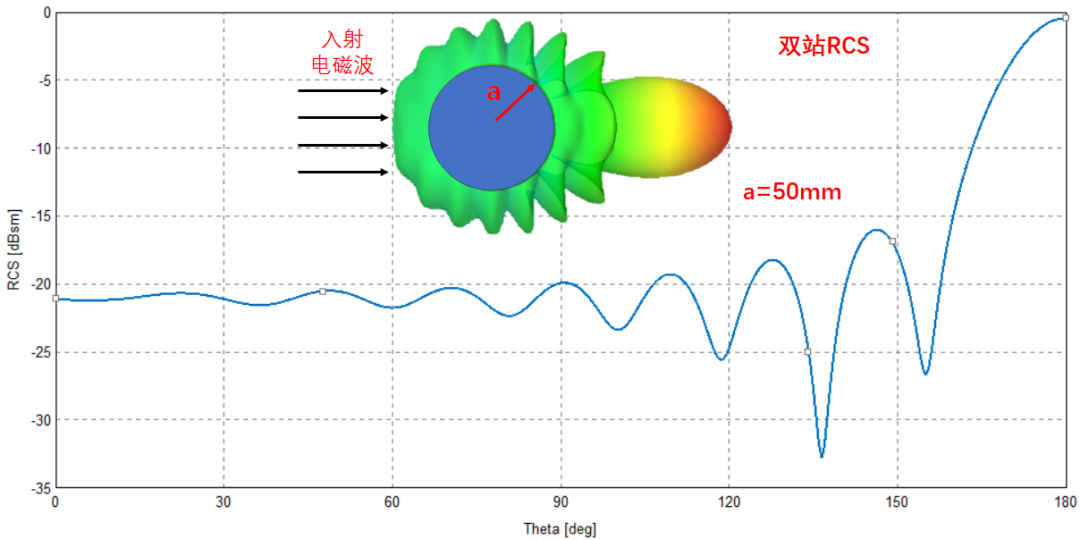
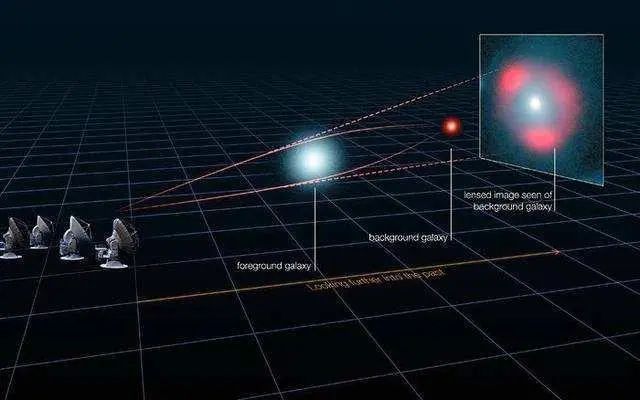
正如往期文章“緣起“收斂性”——Maxwell方程與求解”中所說得那樣,形狀規(guī)則如球形的目標(biāo),尚可以借助高超的數(shù)學(xué)技巧,完成解析計(jì)算,但是一旦模型的外形變化一下,復(fù)雜的外形所帶來的復(fù)雜的邊界條件,會(huì)導(dǎo)致Maxwell方程組無法解析求解。
階段2:近似方法
在那個(gè)“算力”尚不發(fā)達(dá)的年代,類似“全波仿真”的精確計(jì)算方法還沒辦法被實(shí)現(xiàn),近似方法則因?yàn)槠漭^低的“算力需求”而被廣泛使用,其中要數(shù)幾何光學(xué)算法(GO)和物理光學(xué)算法(PO)應(yīng)用最為廣泛。
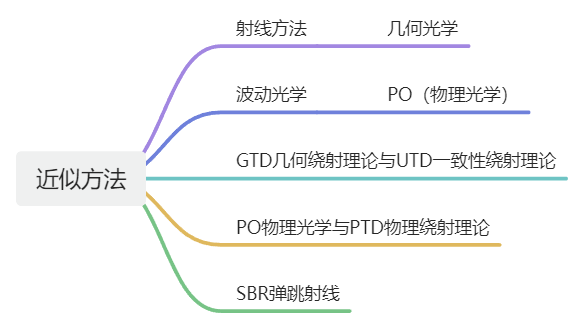
GO(Geometrical Optics幾何光學(xué))
幾何光學(xué)的基本思想基于:高頻電磁波的傳播近似于光,因而波的傳播問題可以采用射線追蹤(Ray-Tracing),從而場(chǎng)的振幅可以根據(jù)波前表面的形狀來確定。顯然,使用幾何光學(xué)方法,陰影區(qū)域中的場(chǎng)完全為零,而被照亮區(qū)域中的場(chǎng)為單獨(dú)的入射場(chǎng)或入射場(chǎng)與反射場(chǎng)的疊加。物體邊沿和尖劈的衍射場(chǎng)被完全忽略,而總場(chǎng)有兩處具有非物理的不連續(xù)性:一處是在亮區(qū)和陰影區(qū)之間的邊界(稱為入射陰影邊界,ISB),另一處是在反射區(qū)和反射不能到達(dá)的區(qū)域之間的邊界(稱為反射陰影區(qū),RSB)。
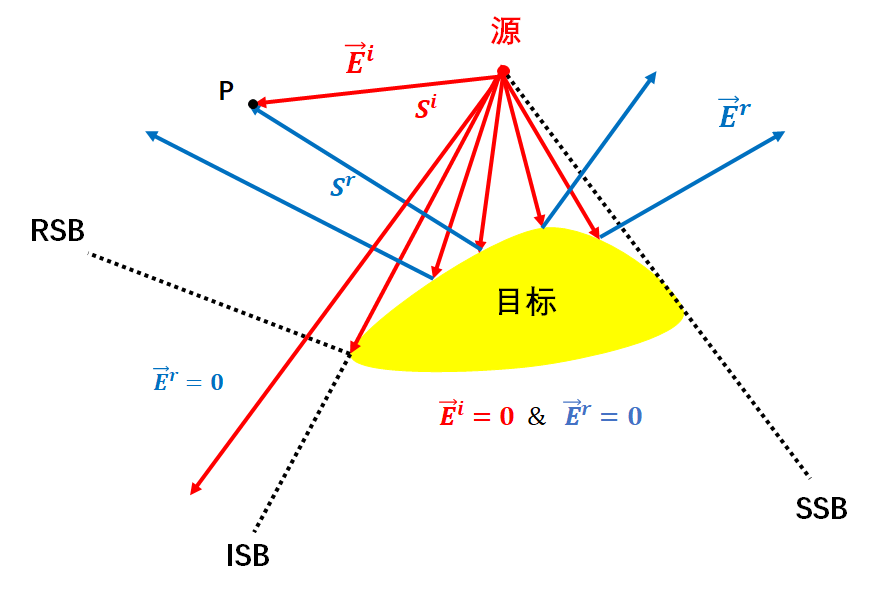
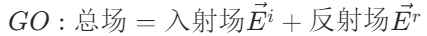
其中入射場(chǎng)和反射場(chǎng)可分別由下列公式求得:
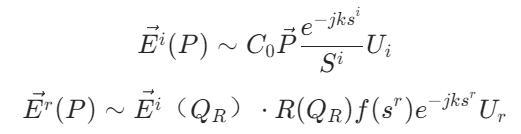
入射場(chǎng)和反射場(chǎng)是否被置零則取決于系數(shù)和的取值:
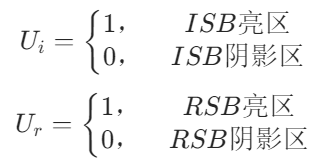
GTD(Geometrical Theory of Diffraction幾何繞射理論)
我們可以在幾何光學(xué)的解中加入衍射場(chǎng)以提高幾何光學(xué)解的精度,由此產(chǎn)生了幾何繞射理論(GTD)。GO的修正繞射線產(chǎn)生于結(jié)構(gòu)不連續(xù)處和材料不連續(xù)處,以及電磁波掠入射光滑凸表面情形,主要有以下集中類型:
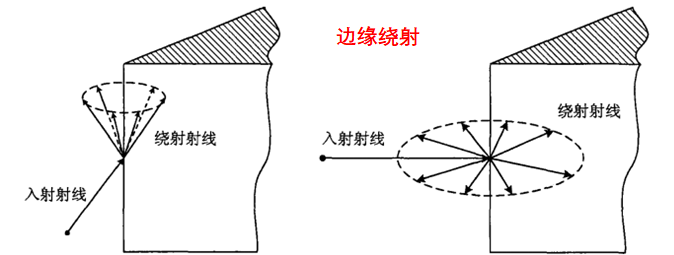
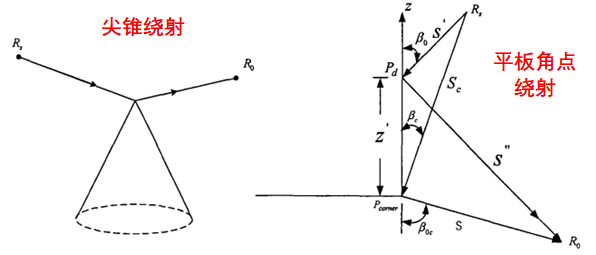
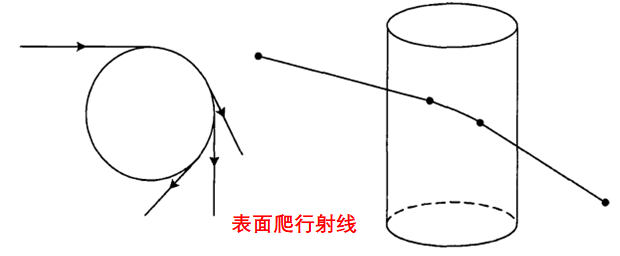
UTD(Uniform Theory of Diffraction一致性繞射理論)
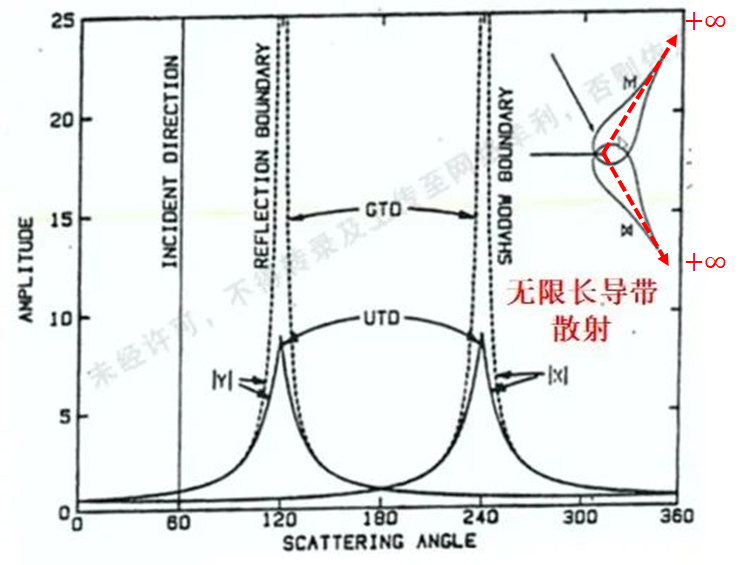
Keller導(dǎo)出的GTD理論,在亮區(qū)和陰影區(qū)的邊界兩側(cè)的過度區(qū)失效,如圖所示,以無限長(zhǎng)導(dǎo)帶的散射為例,按照GTD理論,則會(huì)在兩個(gè)邊界處產(chǎn)生無窮大的散射場(chǎng),與客觀事實(shí)不相符,而UTD則會(huì)通過比例系數(shù)的引入,將過渡區(qū)的場(chǎng)控制在一個(gè)有限大范圍內(nèi),具有更高的計(jì)算精度。
PO(Physical Optics物理光學(xué))
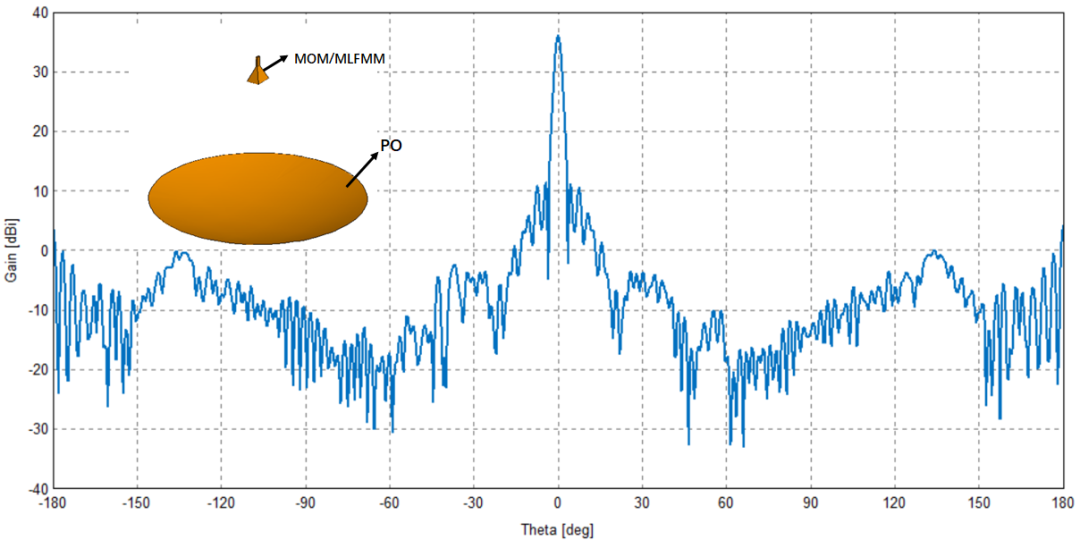
另外一類高頻近似技術(shù)從物理光學(xué)(PO)出發(fā),將電大尺寸導(dǎo)體亮區(qū)表面上的感應(yīng)電流密度近似為,而陰影區(qū)的電流密度近似為。進(jìn)而自由空間中的場(chǎng)分布可以依據(jù)源-場(chǎng)關(guān)系求得:

物理光學(xué)算法被廣泛應(yīng)用于反射面天線輻射特性的計(jì)算,饋源使用全波算法,反射面使用PO算法,兩種算法混合,從而使得電大尺寸的反射面能夠快速獲得相對(duì)準(zhǔn)確的計(jì)算結(jié)果。
PTD(Physical Theory of Diffraction物理衍射理論)
物理光學(xué)理論(PO)近似忽略了幾何不連續(xù)性對(duì)感應(yīng)電流的影響,因此近似的感應(yīng)電流在亮區(qū)和暗區(qū)邊界處存在不連續(xù),這種不連續(xù)影響了計(jì)算結(jié)果的精度,通過在感應(yīng)電流中加入非均勻的邊緣電流,以此來改善物理光學(xué)的計(jì)算精度。
后來聞名世界的第一款隱身戰(zhàn)斗機(jī)F-117的隱身設(shè)計(jì)正是基于此理論而完成的設(shè)計(jì)。
SBR(shooting and bouncing ray彈跳射線算法)
將幾何光學(xué)與物理光學(xué)的方法結(jié)合起來,開發(fā)出了功能強(qiáng)大的算法,用于計(jì)算大尺寸復(fù)雜目標(biāo)的電磁散射,這種混合技術(shù)稱為彈跳射線(SBR)法。在該方法中,從源出發(fā)的入射波用指向物體的射線簇表示。當(dāng)每條射線反彈時(shí),其相關(guān)的振幅和相位均被追蹤,而反彈過程受幾何光學(xué)的約束。在射線與目標(biāo)的每一個(gè)交點(diǎn)應(yīng)用物理光學(xué)法做積分,以確定射線對(duì)散射場(chǎng)或輻射場(chǎng)的貢獻(xiàn),最終解是所有射線貢獻(xiàn)的總和。這種算法已經(jīng)被實(shí)現(xiàn)并廣泛用于計(jì)算雷達(dá)散射特征、大型平臺(tái)上天線的輻射特性和復(fù)雜城市環(huán)境中的電磁波傳播。
依托CST軟件的Asymptotic Sovler(漸進(jìn)求解器)的SBR算法,使用個(gè)人筆記本(8GHz內(nèi)存)即可完成電尺寸達(dá)200倍波長(zhǎng)的縮比艦船模型的散射特性的計(jì)算,計(jì)算效率可以說相當(dāng)之高。
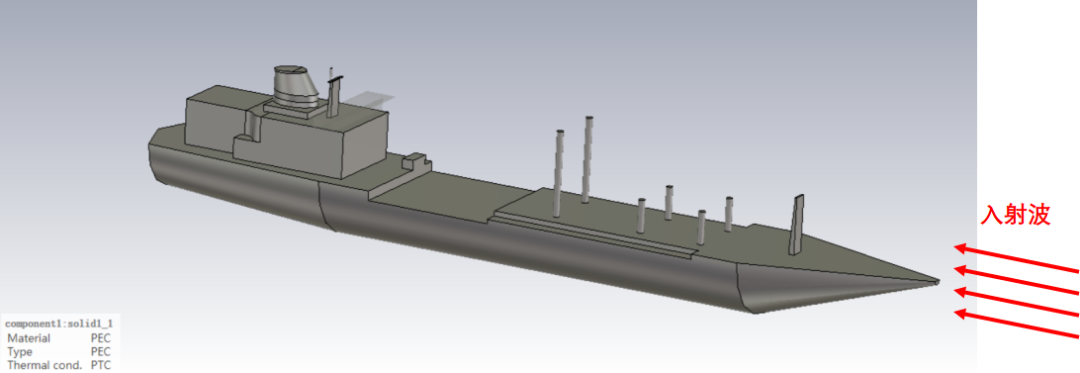
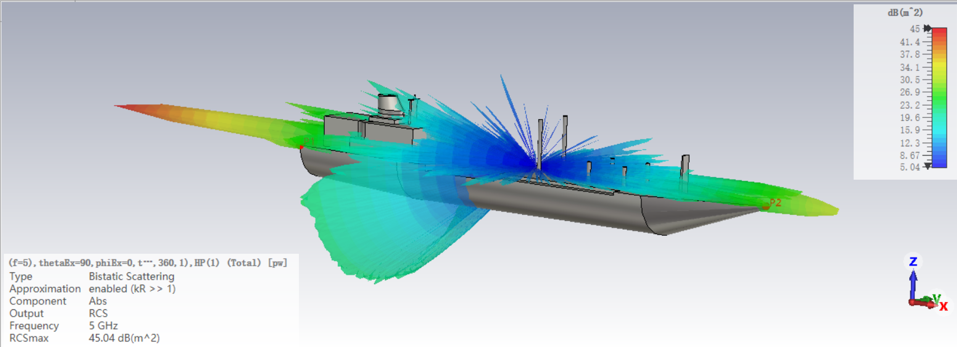
階段3:數(shù)值方法階段
隨著電子計(jì)算機(jī)“ENIAC”的誕生以及其后“計(jì)算能力”飛速發(fā)展,基于“數(shù)值計(jì)算”的全波分析方法也迎來了爆發(fā)式發(fā)展。其中要以時(shí)域有限差分算法(FDTD),有限元算法(FEM)以及矩量法(MOM)發(fā)展最為完備,成為三種最主流的電磁數(shù)值計(jì)算方法。
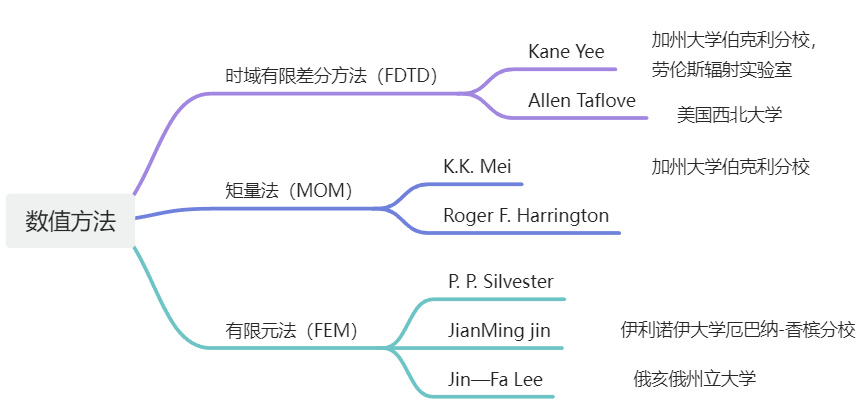
FDTD(時(shí)域有限差分):
1966年,加州大學(xué)伯克利分校的Kane S. Yee教授發(fā)表了基于交替網(wǎng)格的有限差分求解Maxwell方程的論文,1980年,該方法正是被命名為FDTD,全文的被被引用次數(shù)高達(dá)8000次。其離散的對(duì)象直接是時(shí)域微分形式的Maxwell方程組:
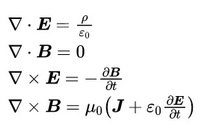
FDTD所使用離散形式也是最為簡(jiǎn)單的立方體網(wǎng)格,每一個(gè)立方體網(wǎng)格就是一個(gè)Yee元胞。
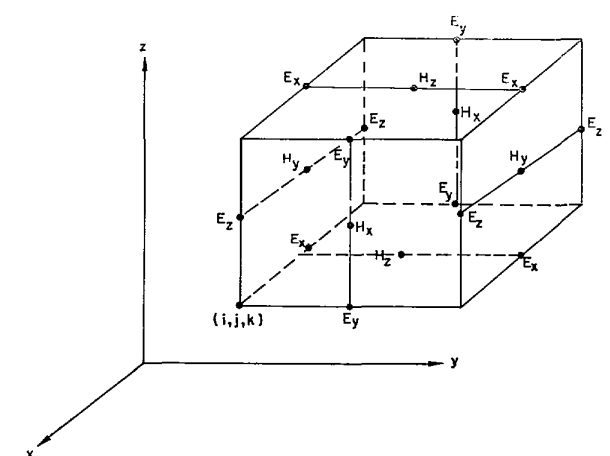
每個(gè)元胞上的電場(chǎng)和磁場(chǎng)可以分解為直角坐標(biāo)系下的三方向分量、、以及、、,上述矢量形式的Maxwell方程即可以展開為標(biāo)量形式的maxwell方程:
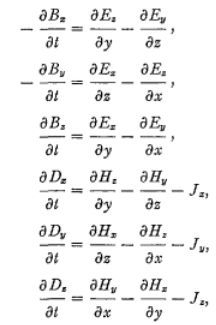
由標(biāo)量形式方程可知,方程中包含了對(duì)電場(chǎng)和磁場(chǎng)分布函數(shù)的時(shí)間微分運(yùn)算以及空間微分運(yùn)算,以電場(chǎng)為例,其中表示對(duì)時(shí)間的微分運(yùn)算,和表示對(duì)空間的微分運(yùn)算,其中和最終均可以拆解為,,的組合,這四種微分運(yùn)算可以用這種通用的表達(dá)式進(jìn)行描述,其可近似為一種簡(jiǎn)單差分形式:
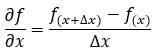
利用這個(gè)近似運(yùn)算,可以將電場(chǎng)對(duì)時(shí)間的微分運(yùn)算轉(zhuǎn)換成前一時(shí)刻的電場(chǎng)與后一時(shí)刻電場(chǎng)之間的運(yùn)算關(guān)系。同樣地電場(chǎng)E對(duì)空間微分運(yùn)算轉(zhuǎn)換成前一位置處的電場(chǎng)與后一位置處的電場(chǎng)之間的運(yùn)算關(guān)系 ,因而只要給定了電磁場(chǎng)的初始值和(初始條件)以及邊界值和(邊界條件),即可以基于差分關(guān)系式,通過不斷的循環(huán)迭代,求解出任意時(shí)刻,任意位置處的電磁場(chǎng)分布和和。
MOM(矩量法):
矩量法的的基本數(shù)學(xué)概念最初在20世紀(jì)初被提出,直到20世紀(jì)60年代中期,隨著K. K. Mei教授等研究人員將其引電磁學(xué)的數(shù)值計(jì)算,才逐漸被大家廣泛關(guān)注,1968年,Harrintong教授在其開創(chuàng)性的專著《Field Computation by Moment Methods》中對(duì)矩量法進(jìn)行了統(tǒng)一闡述。此后,矩量法得到進(jìn)一步發(fā)展,并被廣泛用于求解各類重要的電磁問題。
FDTD和FEM的統(tǒng)治方程均基于微分形式的Maxwell方程,其特點(diǎn)為:1)其通過直接求解“場(chǎng)”(電場(chǎng)或磁場(chǎng))滿足的方程來獲得空間電磁場(chǎng)的分布;2)求解對(duì)象為“微分形式”的Maxwell方程。而MoM則基于一種完全不同的求解思路。
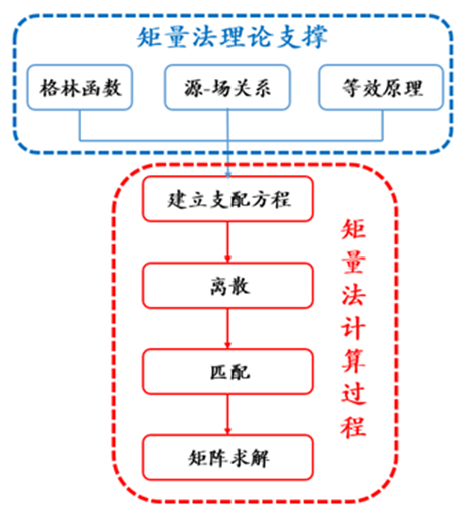
MoM算法理論主要分為兩個(gè)部分:一個(gè)是矩量法支撐理論,主要包括“格林函數(shù)”,“源-場(chǎng)關(guān)系”,“等效原理”三個(gè)子理論,它們是MoM算法如此特立獨(dú)行的根本原因;另一個(gè)則是矩量法計(jì)算理論,主要包括四個(gè)步驟:建立支配方程—>離散—>匹配—>矩陣求解,這與FEM或FDTD算法的求解過程并無明顯區(qū)別。詳細(xì)的推理過程,作者在往期文章“CAE設(shè)計(jì)師的你,有必要了解計(jì)算電磁學(xué)嗎?”中已做了詳盡展示,此處就不在贅述。
FEM(有限元):
1969年,P. P. Silvester使用有限元方法分析了空心波導(dǎo)中波的傳播,這是有限元方法第一次被應(yīng)用于微波工程和電磁學(xué)中。
有限元法基于頻域Maxwell方程,其求解的對(duì)象是時(shí)諧電磁場(chǎng),即電磁場(chǎng)在時(shí)間維度上是周期性分布,循環(huán)往復(fù),無始無終,時(shí)間變量自然也就失去了意義,電磁場(chǎng)只是空間變量的分布函數(shù):
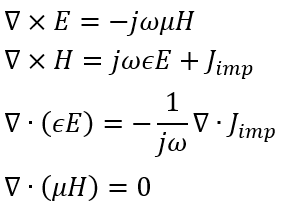
其采用了擬合效果更好的四面體網(wǎng)格對(duì)求解區(qū)域體進(jìn)行剖分。
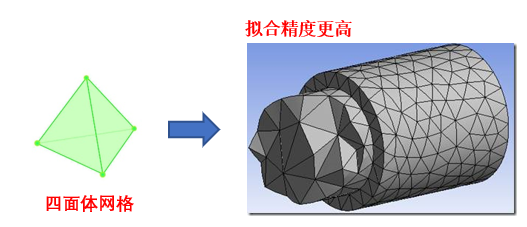
求解空間離散后,緊接著是要空間中待求解的電磁場(chǎng)分布進(jìn)行離散,其核心思想在于尋找到一組展開未知解的基函數(shù):
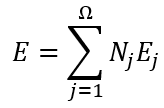
其中為第j條棱邊的切向分量,為待求的切向分量,而為相應(yīng)棱邊上對(duì)應(yīng)的基函數(shù),一旦將所有未知量求解出來,則整個(gè)空間中電場(chǎng)分布就完成了求解。這類似于傅里葉級(jí)數(shù)中使用三角函數(shù)展開任意形式的周期函數(shù),所要做的就是求解每個(gè)基函數(shù)前面系數(shù),然而對(duì)于形狀不規(guī)則的電磁問題,這種基函數(shù)的尋找是及其困難甚至不可能的,有限元法的做法是將目標(biāo)離散成小的單元(三角形,四面體),然后使用非常簡(jiǎn)單的線性函數(shù)或二次函數(shù)來近似這個(gè)單元上的未知解,這些簡(jiǎn)單的基函數(shù)是一種子域基函數(shù),其與上文中傅里葉級(jí)數(shù)展開中的全局基函數(shù)有著很大的不同。利用有限元將目標(biāo)離散,并依據(jù)電場(chǎng)E在空間Ω滿足的波動(dòng)方程和在邊界Γ上滿足的邊界條件條件建立子域基函數(shù)的系數(shù)所滿足的方程組:
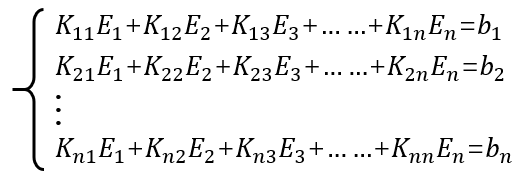
該方程未知量為子域基函數(shù)的系數(shù),完成所有未知量的求解,整個(gè)空間的電場(chǎng)分布既可以表示為子域函數(shù)的疊加。
階段4:快速計(jì)算
傳統(tǒng)的數(shù)值方法(FEM/FDTD/MOM等)精度高,但對(duì)于復(fù)雜電大尺寸目標(biāo),離散需要的未知量數(shù)目多,計(jì)算存儲(chǔ)巨大,效率低。高頻近似方法(GO/GTD/UTD/PO/PTD等)存儲(chǔ)量要求低,計(jì)算速度快,但是精度難以滿足要求。
尋求精確、高效的數(shù)值建模方法是計(jì)算電磁學(xué)領(lǐng)域高度關(guān)注的重要課題,直到世紀(jì)之交,快速算法的的出現(xiàn)以及后面的迅猛發(fā)展,大大降低了計(jì)算的復(fù)雜度和存儲(chǔ)量。由于胡俊教授所在的電子科大電磁輻射/散射研究團(tuán)隊(duì)研究重點(diǎn)聚焦于“積分方程方法”,因此大會(huì)報(bào)告中關(guān)于“快速算法”的一些進(jìn)展主要圍繞“積分方程展開”。積分方程方法的主要特點(diǎn)為:
基于格林函數(shù):自動(dòng)滿足遠(yuǎn)場(chǎng)輻射條件,無需設(shè)置吸收邊界條件,沒有網(wǎng)格截?cái)嗾`差;
等效電流/磁流作為待求未知量:分布在目標(biāo)表面(導(dǎo)體/均勻介質(zhì))或目標(biāo)體內(nèi)(非均勻介質(zhì));
阻抗矩陣元素精確計(jì)算難題:奇異性、近奇異性積分?jǐn)?shù)值計(jì)算;
全局耦合:不同于微分方程產(chǎn)生的稀疏矩陣,積分方程方法導(dǎo)致稠密矩陣,帶來較高的計(jì)算復(fù)雜度和存儲(chǔ)量;
快速算法按照求解方法可以分為迭代求解技術(shù)和直接求解技術(shù),其中迭代求解技術(shù)速度更快但是處理病態(tài)矩陣會(huì)存在不收斂的問題,直接求解技術(shù)不存在收斂性的問題、且適合處理多右端項(xiàng)問題。
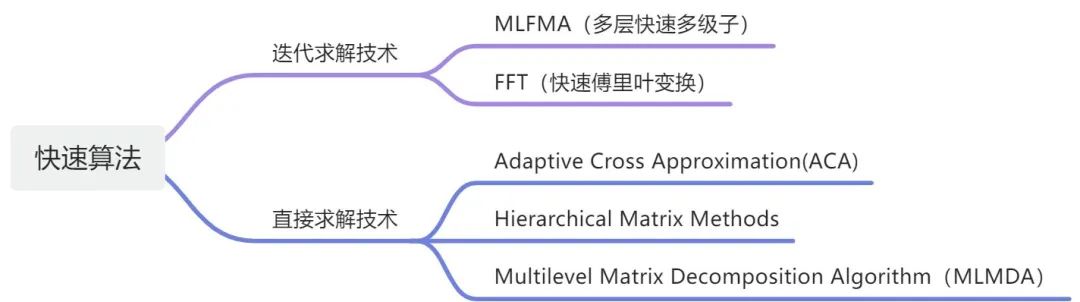
FMM(快速多級(jí)子):
FMM(快速多級(jí)子算法)最初由耶魯大學(xué)的Rokhlin教授提出,用來快速求解粒子間的相互作用和靜態(tài)方程。后來被周永祖(W. C. Chew)教授引入計(jì)算電磁學(xué),極大的降低了計(jì)算復(fù)雜度和內(nèi)存消耗,其后,國(guó)內(nèi)的聶在平教授帶領(lǐng)的團(tuán)隊(duì)獨(dú)立在該領(lǐng)域率先取得突破。
在矩量法中,矩陣向量積的計(jì)算可以等效看成計(jì)算許多電流元的自作用和互作用,即計(jì)算每個(gè)電流元所輻射的被所有電流元接收到的場(chǎng)。快速多級(jí)子基于這樣的基本思想:首先根據(jù)電流元在空間中的位置將其分成若干組,每一組為相互鄰近電流元的集合,然后基于加法定理,將組內(nèi)不同電流元從不同中心發(fā)出的輻射場(chǎng)變換成一個(gè)共同中心輻射的場(chǎng)。
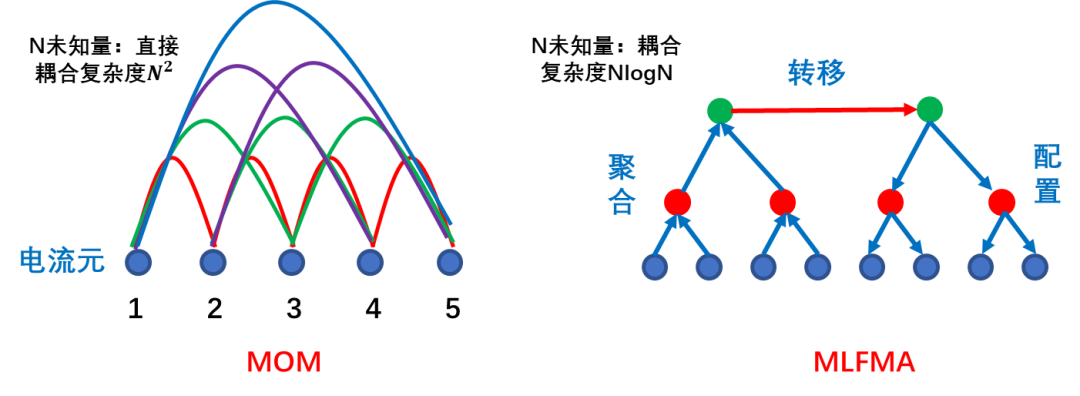
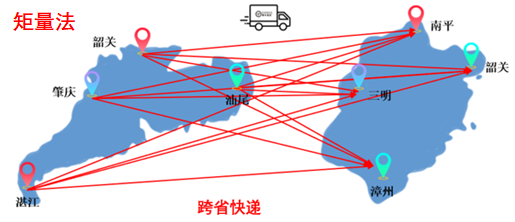
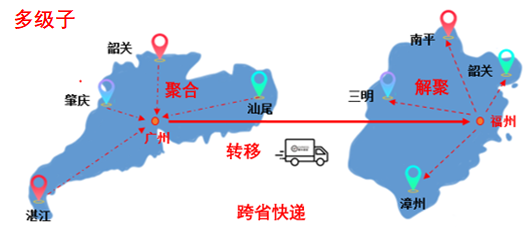
通俗的理解,可以參考往期文章“CAE設(shè)計(jì)師的你,有必要了解計(jì)算電磁學(xué)嗎?”中“跨省快遞”的類比,由圖可知:快速多級(jí)子算法極大的降低單元之間耦合的計(jì)算量。
CG-FFT(共軛梯度-快速傅里葉變換):
歷史上第一個(gè)為計(jì)算電磁學(xué)開發(fā)的快速算法是共軛梯度-快速傅里葉變換法,因?yàn)槠浜?jiǎn)單性,這種方法至今依然是最有效的快速算法。算法的核心思想是將矩量法的矩陣分解成近相互作用和遠(yuǎn)相互作用兩個(gè)部分,這一思想與后來的快速多級(jí)子具有相同的核心思想。
有關(guān)共軛梯度-快速傅里葉變換算法(CG-FFT)的更加深入的數(shù)理推演,受限于作者目前的認(rèn)知水平和精力,只能暫時(shí)先留下相關(guān)學(xué)習(xí)著作和參考文獻(xiàn),以備后續(xù)深入學(xué)習(xí)之需要,互勉。
延申:基于積分方程方法的一些最新進(jìn)展
由于胡俊教授所在的研究團(tuán)隊(duì)主要致力于“積分方程方法”的研究,因此電磁計(jì)算目前最前沿的研究“引申”也主要圍繞積分方程方法(IE)展開。
隨著電磁計(jì)算方法應(yīng)用的日益廣泛,所要面對(duì)的求解問題也越來越復(fù)雜,復(fù)雜目標(biāo)電磁建模面對(duì)的困難主要分為以下幾個(gè)方面:
目標(biāo)由介質(zhì)/金屬組成,多媒質(zhì)問題;
細(xì)微于宏觀結(jié)構(gòu)并存,多尺度問題;
目標(biāo)電大尺寸/超電大尺寸問題;
散射強(qiáng)度較低(隱身),計(jì)算精確性要求高;
多尺度多媒質(zhì)目標(biāo)計(jì)算的收斂性差;
圍繞這些問題,主要的研究思路有:1)發(fā)展區(qū)域分解方法;2)發(fā)展直接求解器......
DDM(Domain Decomposition Method區(qū)域分解算法)
2013年,IEEE Fellow、俄亥俄州立大學(xué)教授Jin-Fa Lee的學(xué)生Zhen Peng發(fā)表了題為《A Discontinuous Galerkin Surface Integral Equation Method for Electromagnetic Wave Scattering From Nonpenetrable Targets》,并于次年獲得“謝昆諾夫最佳論文獎(jiǎng)”,帶動(dòng)了一股積分方程區(qū)域分解方法(IE-DDM)的研究潮。
傳統(tǒng)積分方程方法(Integral Equation),如我們?cè)贔EKO仿真軟件中使用的矩量法(MOM)或基于其上改進(jìn)的多層快速多級(jí)子算法(MLFMM),由于需要保持剖分網(wǎng)格在棱邊上不會(huì)產(chǎn)生電荷積累,因此對(duì)網(wǎng)格的要求是一定要共形,即所有的剖分單元都要共邊。這也有就是為什么使用FEKO對(duì)相接觸的模型進(jìn)行剖分時(shí),必須要union,以確保相鄰模型會(huì)一體化剖分,維持共形條件。
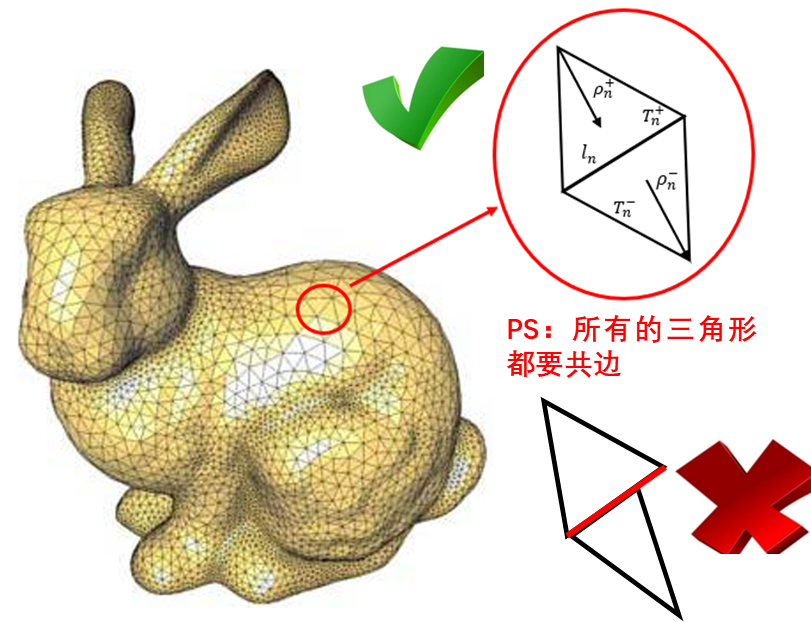
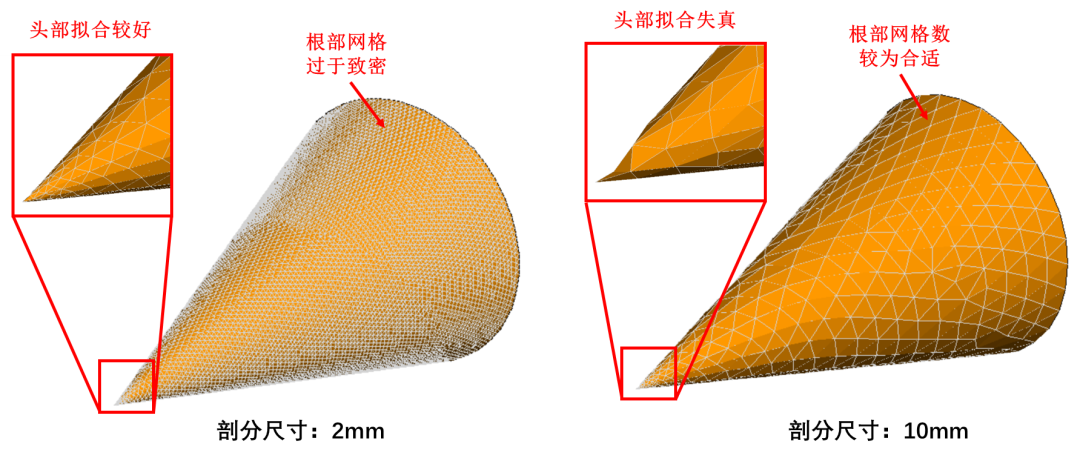
網(wǎng)格共形的要求對(duì)于處理一些類似于“多尺度問題”時(shí)(同時(shí)包含有精細(xì)結(jié)構(gòu)和平坦結(jié)構(gòu)),則會(huì)遇到較大麻煩:如下圖所示的尖錐模型的剖分示意圖,如果需要較好的擬合頭部(精細(xì)結(jié)構(gòu))形狀,則剖分尺寸較小,根部平坦區(qū)域的網(wǎng)格則顯得過于致密,網(wǎng)格數(shù)量多,如果按照根部平坦區(qū)域去設(shè)置剖分尺寸,則網(wǎng)格對(duì)于頭部區(qū)域的擬合則會(huì)出現(xiàn)的失真現(xiàn)象,影響計(jì)算精度;同時(shí),網(wǎng)格尺寸在模型表面過快的增長(zhǎng)也會(huì)帶來矩陣性態(tài)的惡化,從而導(dǎo)致收斂性變差的問題。
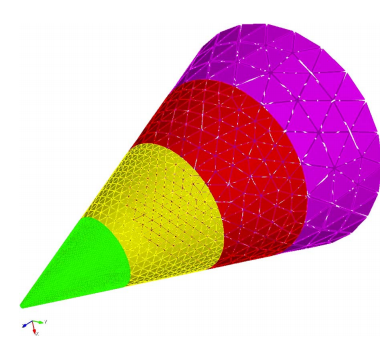
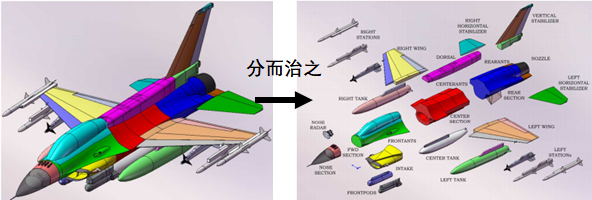
IE-DDM的思想就是按照模型的精細(xì)程度進(jìn)行分類,不同區(qū)域按照不同的剖分尺寸進(jìn)行進(jìn)行剖分,分別計(jì)算,分而治之。其主要克服的難點(diǎn)就在于解決網(wǎng)格不連續(xù)處的電荷積累問題,具體的理論推演可以閱讀Zhen Peng的原文,這里就不作展開了。
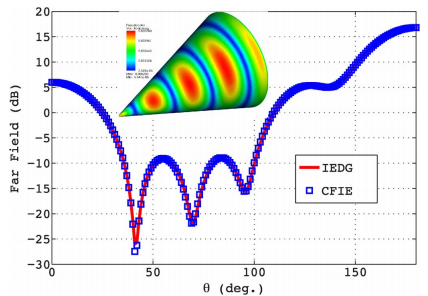
文中,作者挑戰(zhàn)了一個(gè)包含天線罩、機(jī)載天線、進(jìn)氣道、掛載武器等多種令積分方程較為頭疼部件的F-16戰(zhàn)斗機(jī)整機(jī)的的電磁計(jì)算問題。分別計(jì)算了戰(zhàn)機(jī)在3GHz和10GHz頻率下的表面電流分布。

Directive solver(直接求解方法)
圍繞著“積分方程”方法,發(fā)展了兩種求解思路,一種類似于上文中所提到的共軛梯度-快速傅里葉變換算法和快速多級(jí)子算法的迭代求解方法。這類方法計(jì)算速度快、內(nèi)存消耗小,針對(duì)絕大部分電磁計(jì)算問題,不失為最優(yōu)選擇。但是不太適用于以下情況:
病態(tài)矩陣系統(tǒng)(強(qiáng)諧振、多尺度結(jié)構(gòu))
多右端項(xiàng)問題(單站RCS、不確定性量化)
系統(tǒng)部分更新(逆散射問題、閉環(huán)優(yōu)化)
遇到這些情景時(shí),高效的直接求解算法可能成為更好的選擇。直接求解方法圍繞散射矩陣,直接開展計(jì)算,因此不存在收斂的問題,且對(duì)于多右端項(xiàng)問題,只需計(jì)算一種狀態(tài),其余狀態(tài)即可快速給出,因此狀態(tài)非常多時(shí),也不失為一個(gè)好的選擇。
高效的直接求解算法,則是針對(duì)“傳統(tǒng)直接求解算法”矩陣計(jì)算速度太慢、內(nèi)存消耗太大的問題而開展的,一般基于低秩壓縮,主要方法有:
改進(jìn)型HODLR矩陣方法
增強(qiáng)型Skeletonization方法
Butterfy方法
審核編輯:劉清
-
電磁波
+關(guān)注
關(guān)注
21文章
1470瀏覽量
53902 -
電磁學(xué)
+關(guān)注
關(guān)注
1文章
108瀏覽量
14219 -
RCS
+關(guān)注
關(guān)注
0文章
57瀏覽量
12735 -
cae軟件
+關(guān)注
關(guān)注
0文章
9瀏覽量
7037 -
求解器
+關(guān)注
關(guān)注
0文章
77瀏覽量
4548
原文標(biāo)題:電磁計(jì)算方法的發(fā)展與展望
文章出處:【微信號(hào):EMC_EMI,微信公眾號(hào):電磁兼容EMC】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
電阻器的工作原理與計(jì)算方法
波特率的定義和計(jì)算方法 波特率與數(shù)據(jù)傳輸速度的關(guān)系
FPGA門數(shù)的計(jì)算方法
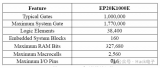
電流計(jì)算方法與配線法的區(qū)別
電荷放大電路的帶寬 和IV轉(zhuǎn)換電路帶寬計(jì)算方法不一樣嗎?
使用位置傳感器輸出數(shù)據(jù)的角度計(jì)算方法

DCS系統(tǒng)I/O點(diǎn)數(shù)計(jì)算方法與原則
相電流和線電流的關(guān)系計(jì)算方法
生物膜的電路中time常數(shù)的計(jì)算方法
步進(jìn)電機(jī)步進(jìn)驅(qū)動(dòng)器計(jì)算方法
儲(chǔ)能容量的計(jì)算方法
電壓探頭延遲計(jì)算方法及應(yīng)用





 電磁計(jì)算方法的發(fā)展
電磁計(jì)算方法的發(fā)展











評(píng)論