正則表達式和EXCESS系統

尾數部分

? 「尾數部分」 使用 「正則表達式」 ，可以將表現形式多樣的浮點數統一為一種表現形式。

?

例如，十進制數0.75就有很多表現形式。

雖然他們表示的都是 「同一個數值」 ，但因為表現方法太多，計算機在處理時會比較麻煩。

因此，需要制定統一的規則：

?十進制數的浮點數應該遵循：「小數點前面是0，小數點后面第一位不能是0」

?

也就是說，只能用 「尾數」 部分是0.75、 「指數」 部分是0的方法來表示。即0.75 × 100

?在二進制數中，我們規定：「將小數點前面的值固定為1的正則表達式」

?

具體來講，就是將二進制數表示的小數 「左移」 或 「右移」 （邏輯移位）數次后， 「整數部分」 的第一位變成1， 「第二位之后都變成0」 。

?而且， 「第一位的1在實際的數據中不保存」 ，因此省略該部分后就可以節省一個數據位，從而可以表示更多的數據范圍。

?

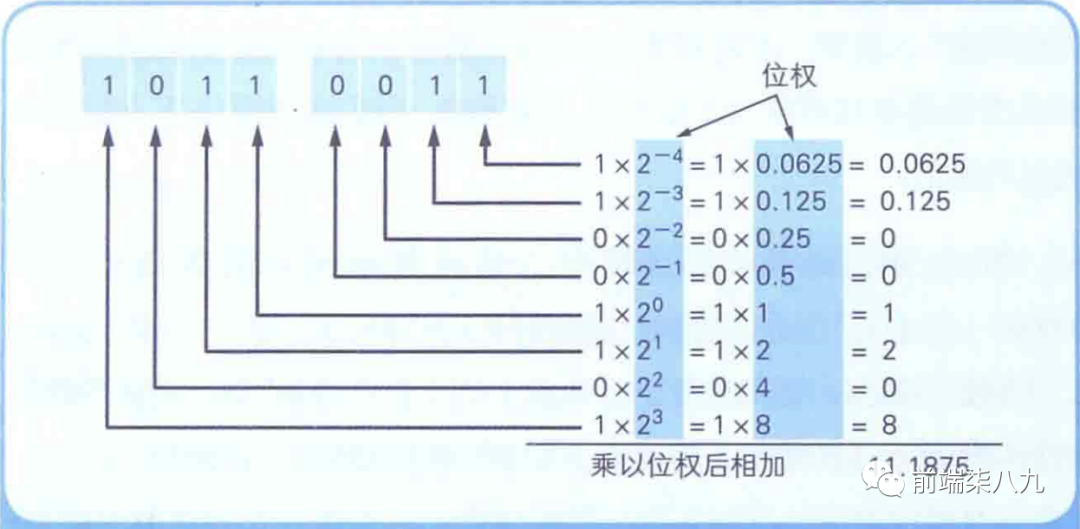
我們，看一下1011.0011如何用單精度浮點數的正則表達式來表示 「尾數部分」 。

指數部分

「指數部分」 中使用的是EXCESS系統，使用這種方式主要是 「為了表示負數時不使用符號位」 。

在某些情況下，在指數部分，需要通過 「負〇〇次冪」 的形式來表示負數。

? 「EXCESS系統」 表現是指，通過將指數部分表示范圍的 「中間值」 設置0，使得負數不需要用符號來表示。

?

也就是說，當 「指數部分」 是8位單精度浮點數時，最大值11111111=255的1/2,即01111111=127(小數部分舍棄)表示的是0。

我們再來一個例子說明。假設有這樣一個游戲，用1~13(A~K)的撲克牌來表示負數。此時，我們把 「中間」 的7當做0。那么10表示+3，3表示-4。

單精度浮點數指數部分的EXCESS系統表現

實際運用

我們來一起看看如何用單精度浮點數來表示十進制數0.75。

• 「符號位」 ：因為0.75是正數，所以符號位是0

0.75轉換成二進制正則表示為1.1×2-1,按照前面介紹的就很容易知道下面的各個數值。

• 「指數部分」 ：為-1，但是用EXCESS表示的話，就變成了01111110。換算為十進制為126。而EXCESS系統中，126代表-1
• 「尾數部分」 ：根據正則表達式的規則，小數點前面的第1位是1,因此 「尾數部分」 1000···實際上表示的是1.1000···

二進制數和十六進制數關系

在以 「位」 為單位表示數據時，使用二進制數很方便，但如果位數太多，看起來很麻煩。因此，在實際程序中，經常用 「十六進制數」 來替代 「二進制數」 。

在一些高級語言中，只需要在數值的開頭加上0x就可以表示十六進制數。

?二進制數的4位，正好相當于十六進制數的1位。

?

由此可見，通過使用十六進制數，二進制數的位數能夠 「縮短」 至原來的1/4。

用十六進制數表示二進制 「小數」 時，小數點后的二進制數的4位也同樣相當于十六進制數的1位。「不夠4位時用0填補二進制的低位」