大地坐標系之間的轉換一直是導航領域十分關注的課題，在GPS的應用中有著必不可少的作用。 隨著GPS越來越廣泛的使用，其精度要求也越來越高，大地坐標系之間的轉換的重要性日趨明顯，甚至許多項目的成敗完全取決于坐標系統的轉換和轉換精度。 隨著計算機技術及移動互聯網的飛速發展，數據的處理和信息的傳遞突破了時間和地域的限制，作為信息時代的產物和寵兒，全球定位系統得到了空前的發展和應用，為空間定位提供了準確、可靠的數據，而這些準確、可靠的數據更需要算法的支持。 在手機軟件測量大師的開發過程中，我有幸涉獵到該領域的算法知識。 在這里我將分別從坐標系統基本理論、不同坐標系及不同橢球間的坐標轉換、測量大師中的坐標轉換方法及參數計算過程這幾個方面來進行簡單介紹。

一坐標系統基本理論

1、地球橢球的基本概念

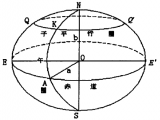
在測量學中，把用來表示地球的橢球稱為地球橢球，它是地球的數學表示，是經過一定選擇的旋轉橢球。 參考橢球是具有一定的幾何參數、定位以及定向的用來表示某一大地面的地球橢球。 各個國家根據局部的天文、大地和重力的測量資料，研究當地大地水準面的情況，確定一個與地球橢球接近的橢球，用來表示地球的參考形狀及大小，以此作為處理大地測量成果的依據，一般稱這個橢球的外表面為參考橢球面。 參考橢球只能較好的接近大地水準面，并不能反映大地體的一切情況。

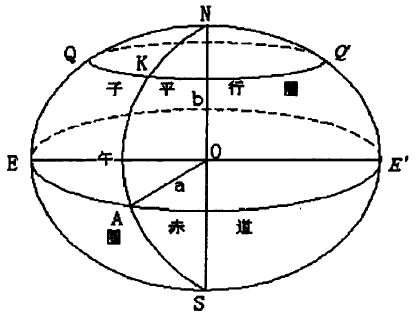
圖1 參考橢球

旋轉橢球是某橢圓繞其自身短軸旋轉而成的幾何形體。 子午橢圓的五個基本元素分別為:長半軸a、短半軸b、扁率f、橢圓第一偏心率e、橢圓第二偏心率e\'。 這其中，a, b為長度元素，f體現了橢球的扁平程度。 e和e\'為橢圓的焦點偏離中心的距離與其半徑的比值。 要確定旋轉橢球的形狀和大小，只要知道這五個基本參數中的一個長度元素和其他任意一個參數便足夠了。 如圖1所示，O為橢球中心，NS是旋轉軸，a是長半軸，b是短半軸。 子午面是通過橢球旋轉軸的平面，其與橢球面的交線叫做子午圈； 平行圈是橢球面與垂直于旋轉軸的平面截得的圓，這其中經過橢球中心O的平行圈叫做赤道。

2、常用坐標表現形式

為了表示橢球面上點的位置，必須建立相應的坐標系，選用不同的坐標系，其坐標表現形式也不同。 橢球點上的位置，在大地測量學中通常采用的坐標系有大地坐標系，空間直角坐標系，平面直角坐標系等。 在同一參考橢球基準下，大地坐標系，空間直角坐標系，平面直角坐標系是等價的，是一一對應的，只是不同的坐標表現形式。

(1)大地坐標系

大地坐標系是大地測量的基本坐標系，是全世界公用的最方便的坐標系統，對于研究地球形狀、編制地圖和大地測量的計算等方面都有很大作用。 如圖2所示在大地坐標系中，空間中任意點的位置采用大地緯度B、大地經度L和大地高H來表示。 大地緯度是指空間中某一點P的法線與赤道面的夾角，赤道以北叫做北緯； 赤道以南叫做南緯。 大地經度是指P點所在的子午面與參考橢球的起始子午面所構成的夾角，起始子午面以東叫做東經，起始子午面以西叫做西經。 大地高H即空間的點沿著參考橢球的法線方向到橢球面的距離，由橢球面起算，向外為正，向內為負。 它與正高H正和正常高H正常，存在以下關系: H=H正+N(大地水準面差距)

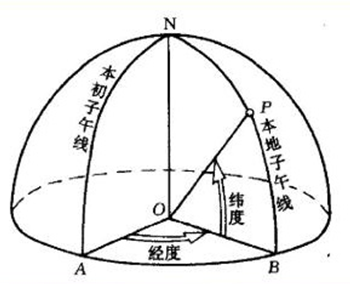
圖2大地坐標系示意圖

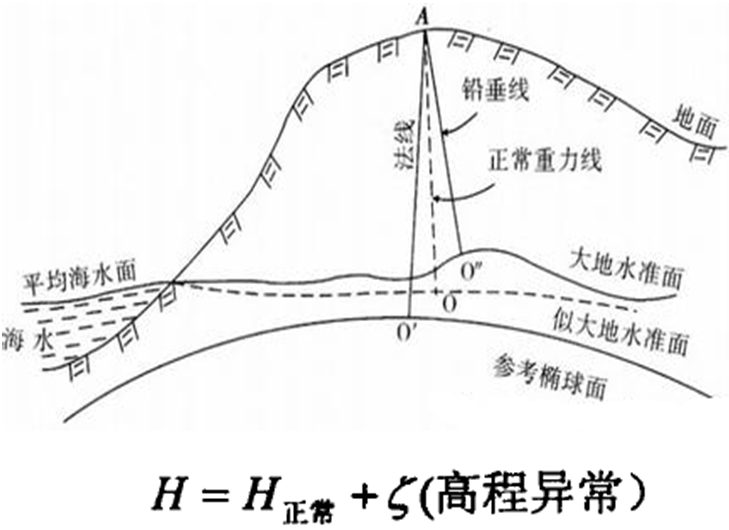
圖3大地高程示意圖

(2)空間直角坐標

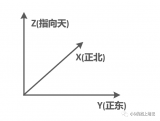
空間直角坐標系的坐標原點為橢球的中心，X軸為赤道面和起始子午面的交線; 將在赤道面上并與X軸垂直的方向定為Y軸; 坐標系的Z軸為橢球的旋轉軸，由此構成右手直角坐標系0-XYZ。

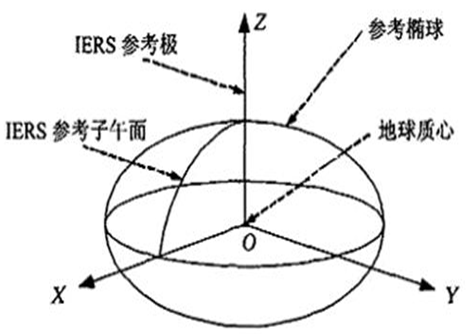
圖4空間直角坐標系示意圖

(3)平面直角坐標

在小范圍內進行測量工作時如果用大地坐標來描繪點的空間位置是不適宜的，因此經常采用平面直角坐標。 測量學中的平面直角坐標系是利用某種投影變換例如高斯投影如圖所示，將空間坐標經數學變換映射至平面上，投影變換的方法很多，我國通常采用高斯投影，因此在我國平面直角坐標系通常也稱為高斯平面直角坐標系。 一般選擇高斯投影平面作為坐標平面，與數學中的平面直角坐標系不同的是，其x軸為縱軸，上(北)為正，Y軸為橫軸，右(東)為正，方位角是從北方向為準按順時針方向計算出的夾角。

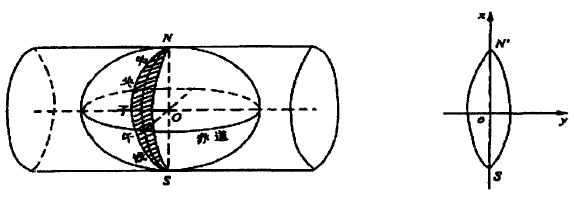
圖5高斯投影平面直角坐標系

二不同坐標系及不同橢球間的坐標轉換

測量坐標轉換一般包括兩方面的內容:坐標系轉換和坐標基準轉換。 同一坐標基準下，空間點不同表現形式的轉換叫做坐標系轉換。 如在WGS-84坐標系下，某點的大地坐標(B, L, H)與空間直角坐標(X,Y, Z)之間的轉換。 坐標基準轉換則為在不同坐標基準下的同一坐標表現形式的轉換，必須求定兩個不同坐標基準的轉換參數才能進行轉換。 如1954北京坐標系標系與2000國家大地坐標系下空間直角坐標的轉換。 因此，從理論上講，結合坐標系轉換和坐標基準轉換，便能在數據量足夠多并精確的條件下，實現任意兩個坐標基準之間不同坐標形式的轉換。 具體流程如圖6所示：

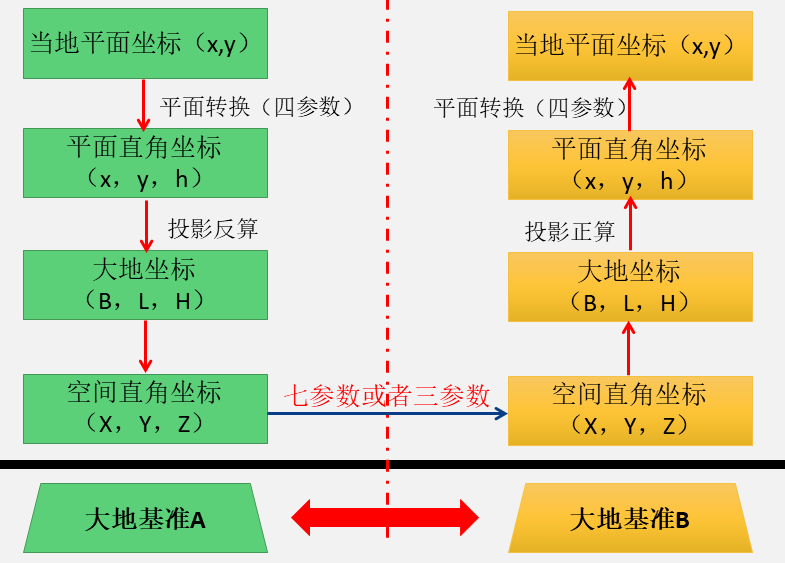
圖6 坐標系轉換及基準轉換關系

我們都知道，在工程上使用的坐標主要是小區域范圍的平面投影坐標，因此在接收機獲取到WGS84的經緯度坐標時需要做進一步的坐標轉換，我們測量大師已經滿足需求。 這里介紹一下測量大師中涉及的坐標轉換方法，其包括以下三種：四參數+高程擬合法（一步法）、七參數+四參數+高程擬合法（兩步法）、七參數法。

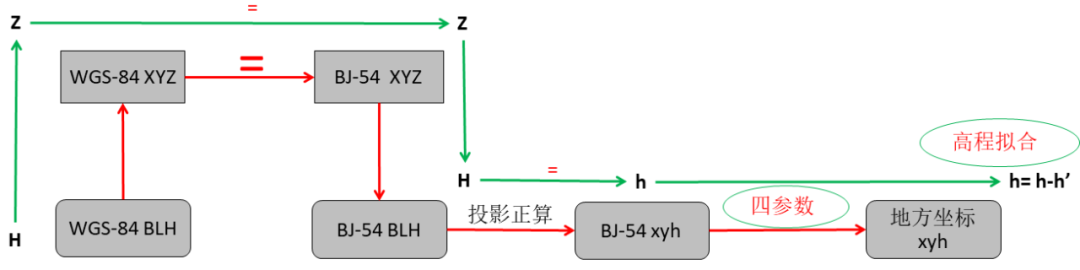
圖7四參數+高程擬合

這里以WGS-84橢球下的坐標系轉換到北京54橢球坐標系的過程為例來介紹這三種轉換過程。 如圖7所示，由接收機獲取到的WGS-84的大地坐標（BLH）經過坐標系轉換成WGS-84空間直角坐標系，然后直接賦值給北京54空間直角坐標系，在北京54橢球參數下進行空間直角坐標向大地坐標（BLH）轉換，然后在進行高斯投影，從而獲得平面直角坐標。 這里獲取的投影坐標是有誤差的，因此要通過提供四參數以及高程擬合參數分別對平面坐標及高程異常進行水平垂直矯正。

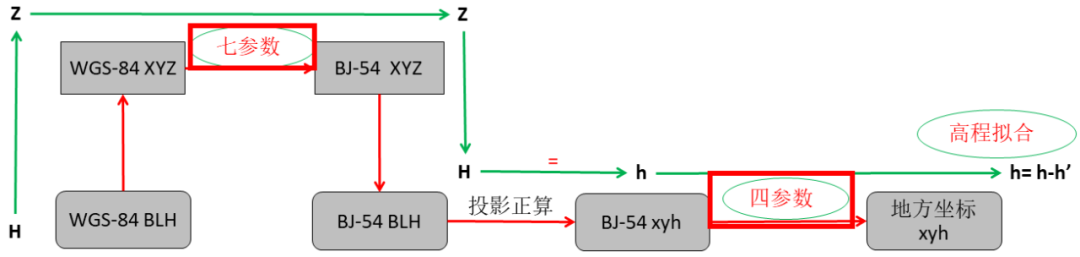
圖8七參數+四參數+高程擬合

如圖8所示，在WGS-84空間直角坐標向北京54空間直角坐標轉換過程中需要已知的橢球間的轉換七參數進行轉換，然后在最后進行平面及高程矯正。 圖9中，提供橢球間轉換七參數即可，轉換結果不進行矯正。

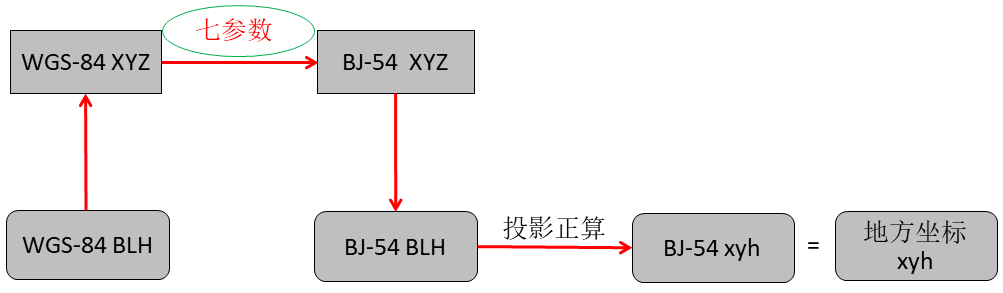
圖9七參數法

三
參數計算過程

由前面可知，坐標轉換過程中需要提供四參數、七參數以及高程擬合參數，那么這些參數是怎么得到的呢？ 這節就開始解密參數的計算過程。

在使用測量大師做參數計算時，當選擇四參數+高程擬合參數的方法時，四參數及高程擬合參數計算如圖10所示。 首先要有至少兩組GNSS坐標和已知控制點坐標； ①先按照紅色箭頭的流程進行坐標轉換，當轉換到北京54平面投影坐標時，開始根據轉換得到的坐標和已知的控制點平面坐標進行計算四參數。 ②再按照綠色箭頭流程進行高程傳遞，根據轉換得到的高和已知高計算出高程異常值，最后根據高程擬合算法進行計算擬合參數。 其中這里的高程擬合方法包括：加權平均值法、平面擬合法、曲面擬合法、帶狀擬合法。

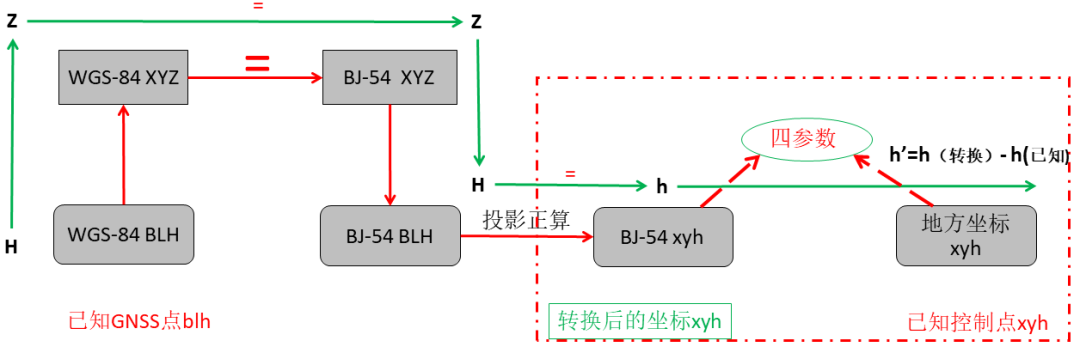
圖10 四參數+高程擬合計算圖解

當選擇七參數+四參數+高程擬合參數法時，算法流程如圖11所示：首先要確保至少三組GNSS坐標和已知控制點坐標； ①先按照紅色箭頭流程，左側WGS-84大地坐標轉換成WGS-84空間直角坐標，右側由地方控制點坐標直接通過逆投影轉換成北京54大地坐標，然后再轉成北京54空間直角坐標，最后通過至少三組WGS-84空間直角坐標和北京54空間直角坐標計算出七參數； ②再按照綠色箭頭流程，將已知GNSS坐標轉換成WGS-84空間直角坐標，再使用①流程計算出的七參數進行基準轉換成北京54空間直角坐標，并進一步轉換成北京54平面坐標，從而與地方平面坐標進行對比計算出四參數； ③最后按照藍色箭頭流程通過七參數和四參數進行坐標轉換，計算出高程異常值，進行高程擬合從而得到高程擬合參數。

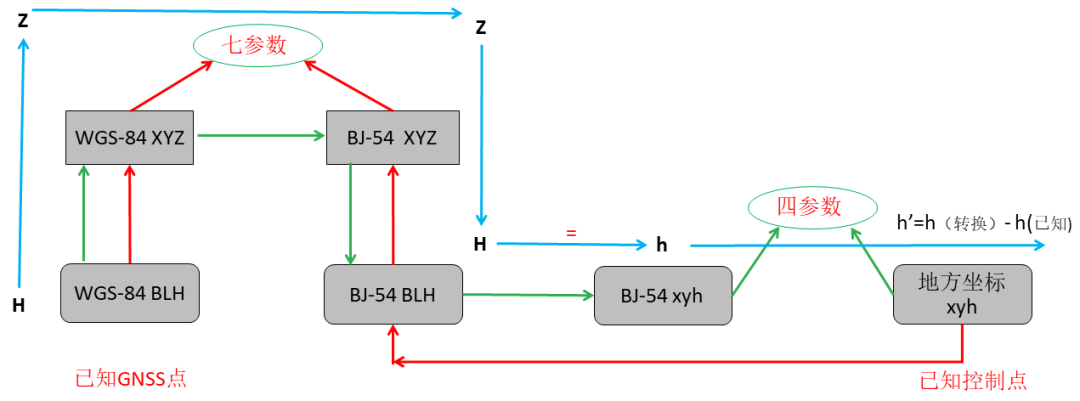
圖11七參數+四參數+高程擬合計算圖解

四成果展示

測量大師參數計算升級版本已經發布，這里展示一下我們的成果。 參數計算方法已實現四參數+高程擬合法、七參數+四參數+高程擬合法、七參數法如圖12所示，高程擬合方法已實現加權平均法、平面擬合法、曲面擬合法、帶狀擬合法以及保留上一版本的垂直平差法如圖13所示。 由圖14、15、16可以看出我們的軟件計算精度比肩同行軟件，已經滿足工程需求及市場需求。

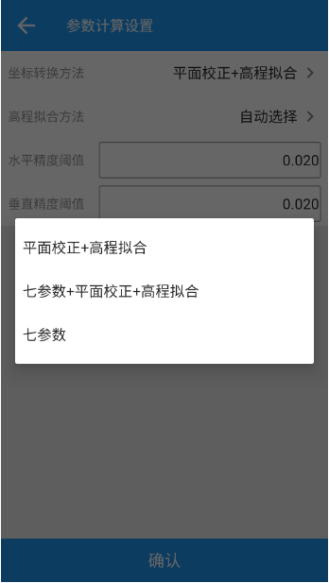
圖12坐標轉換方法

圖13高程擬合方法

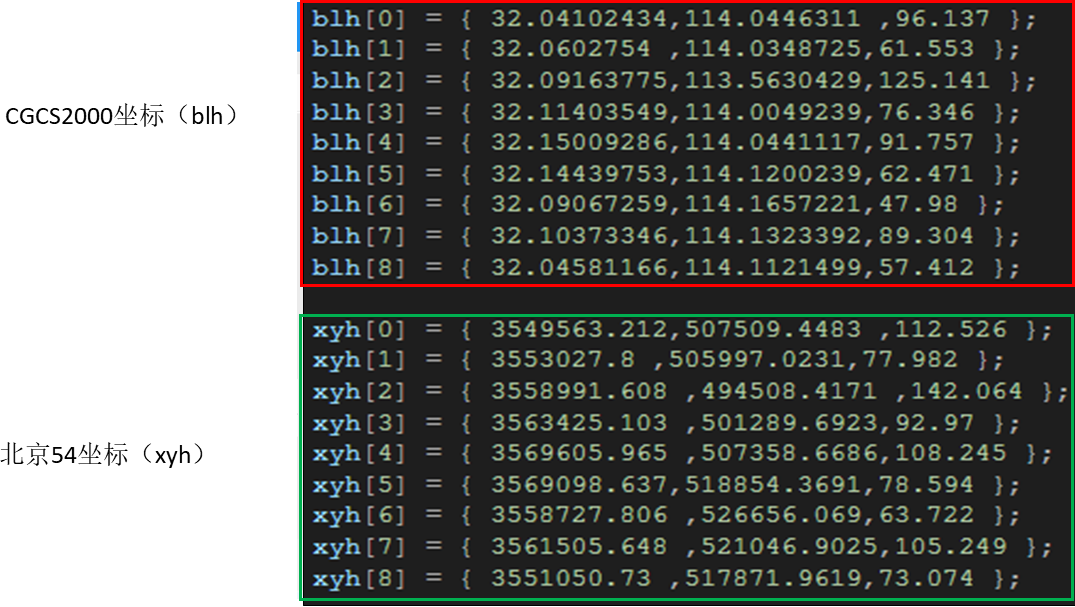
圖14 實驗數據

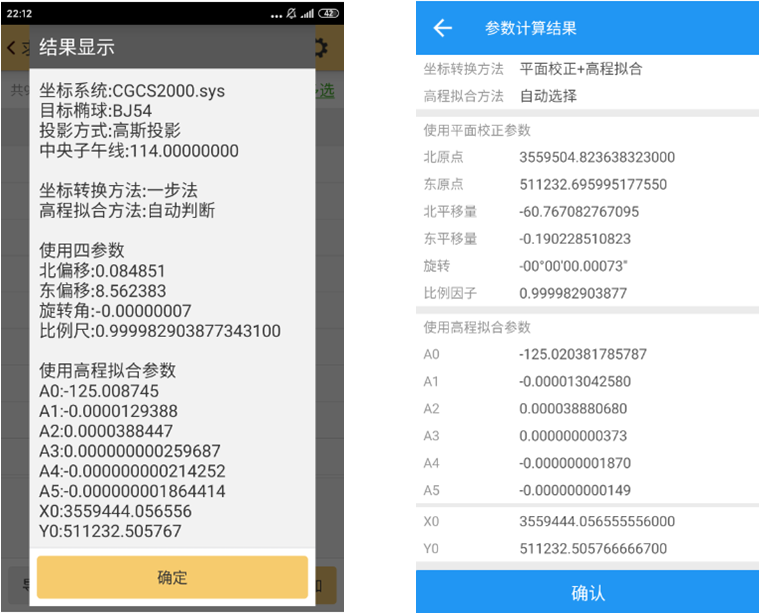
圖15四參數+高程擬合法

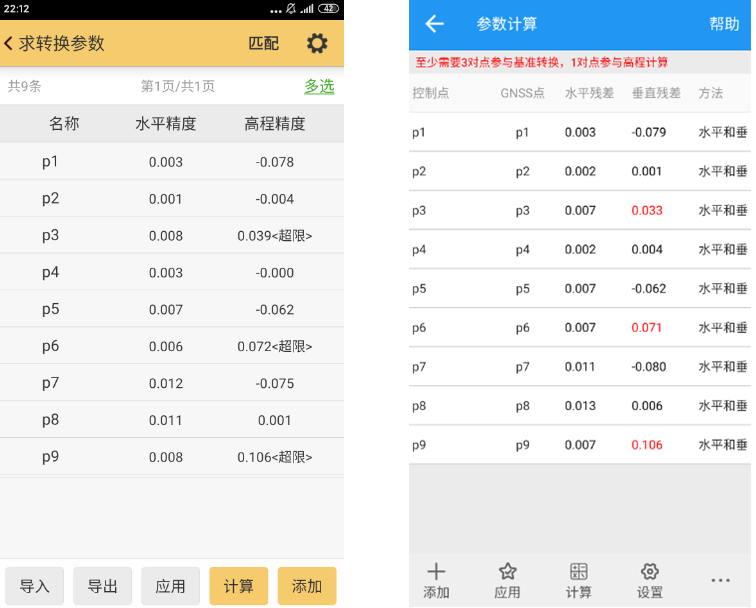
圖16四參數+高程擬合法

審核編輯：湯梓紅