在上一篇文章中詳細描述了帶阻性負載時米勒平臺是怎樣的，對各階段做了定量分析，相信看過的同學應該會有所收獲。今天我們來聊一聊帶感性負載時米勒平臺是怎樣的。

同學留言

一位同學留言說即便用感性負載也仿真不出理論曲線，仿真結果和阻性負載差不多。

感謝這位同學的留言，相信這位同學應該是實際動手仿真過，才有這樣的疑問。那到底是不是這樣的呢？大家不妨跟著二火一起動起來，咱們搭個模型試試，畢竟硬件微講堂還是崇尚用理論+數據的方式來論證觀點。

搭建模型

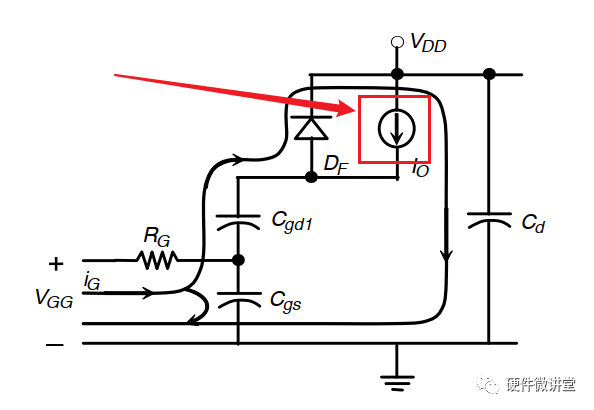
還記得上一篇阻性負載時所搭建的仿真模型么？如下圖所示：

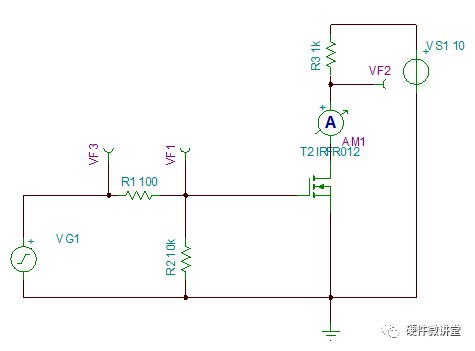
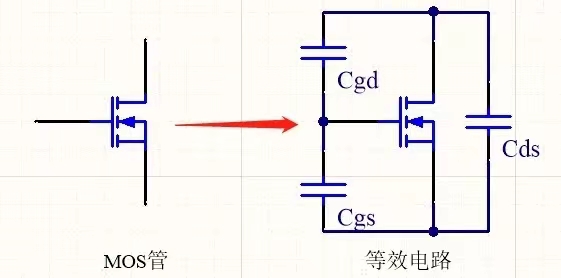
我們只需要把電路中的R3更換為電感L1即可。為了避免電感在MOS管開關過程中產生巨大的反向電動勢，我們需要給電感L1配上一個續流二極管D1。

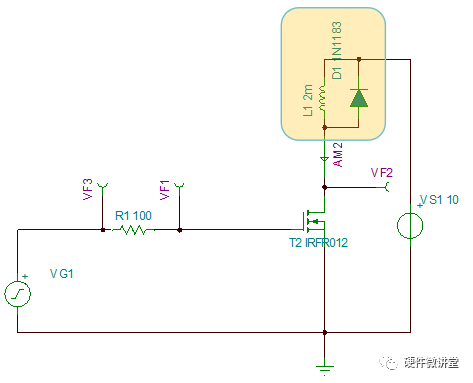
有的同學會問為什么會有巨大的反向電動勢？這里不做過多展開，只說兩點，其他的請自行腦補。

①電感中的電流不能突變，但電流變化率dI/dt可以突變；

②U=LdI/dt。

仿真電路調整好后，再進行參數設置。調整下VG1，設置為幅值為5V的方波，用于驅動MOS管的柵極。

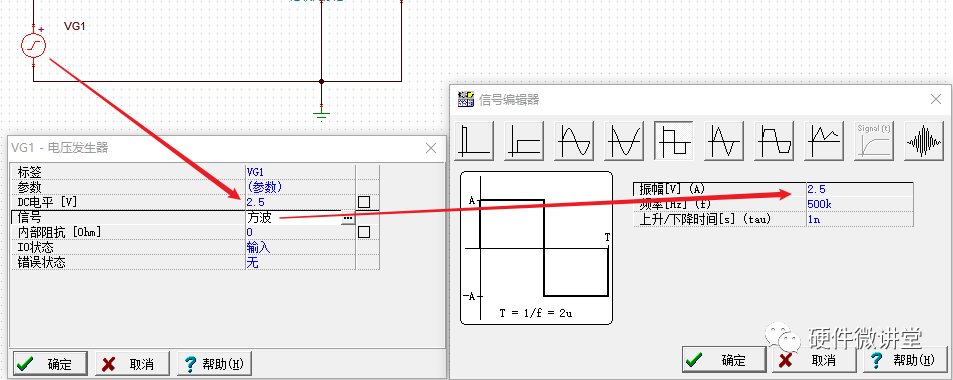
VS1是電壓源，10V就夠用，不用調整。L1取值2mH，這取值是隨意取的。到這里，仿真模型就算搭建完畢，下一步開始仿真。

仿真驗證

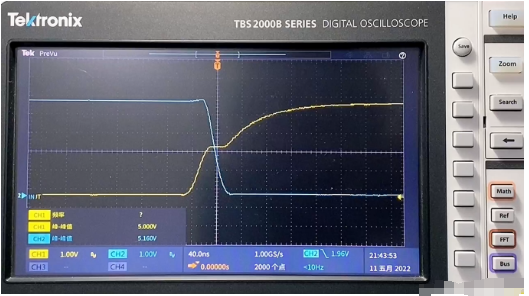
通過“分析”--“瞬時分析”，設置10us的仿真時間，執行即可得到如下波形。而黃框中的部分即為米勒平臺所對應的Vgs、Id、Vds波形。

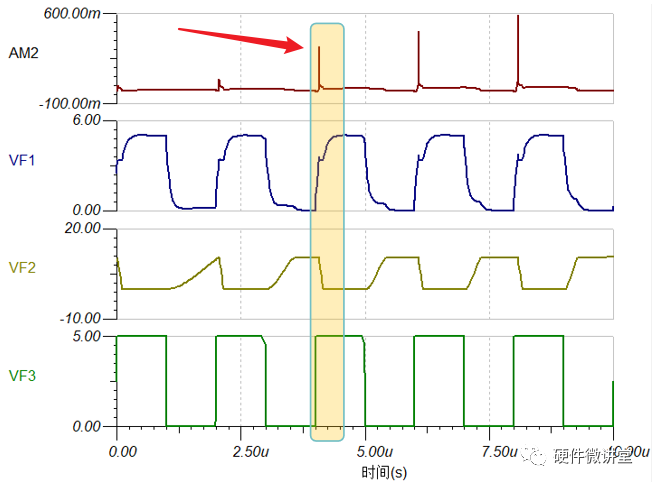
對黃色區域進行局部放大，可以得到如下波形。同樣可以分為4個階段：

階段①：Vgs

階段②：Vgs>Vth，Vds>Vgs-Vth，飽和區;

階段③：Vgs>Vth，Vds>Vgs-Vth，飽和區;

階段④：Vgs>Vth，Vds

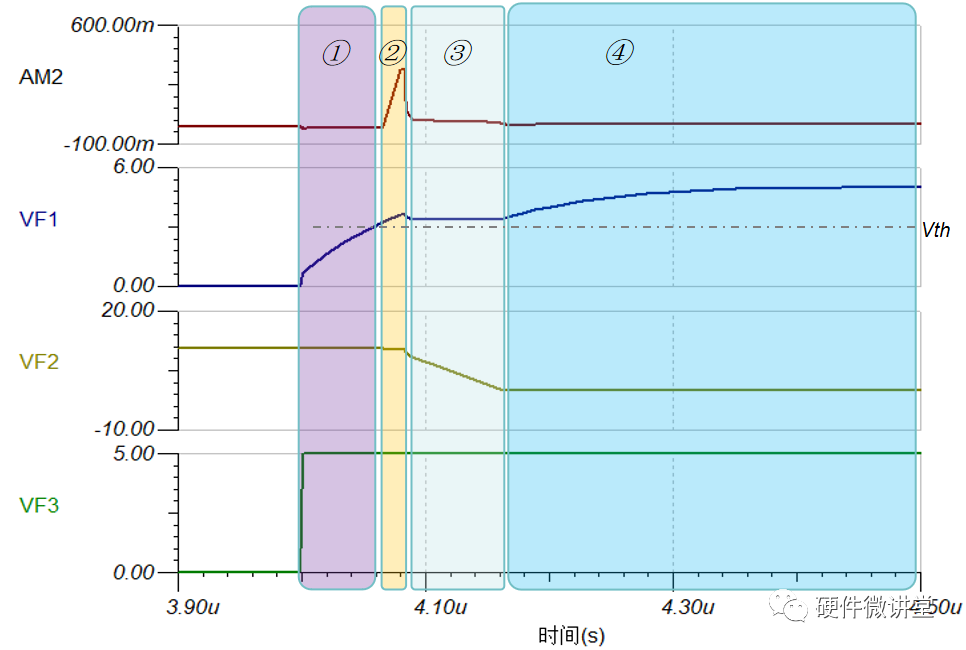
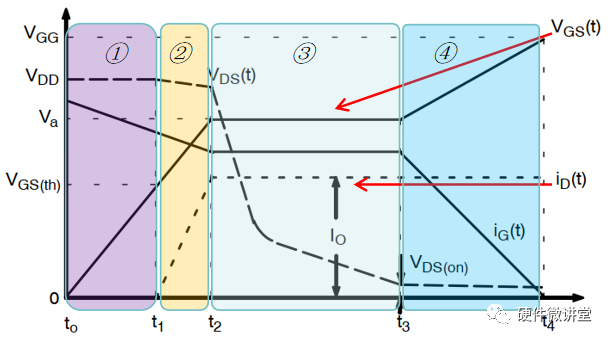
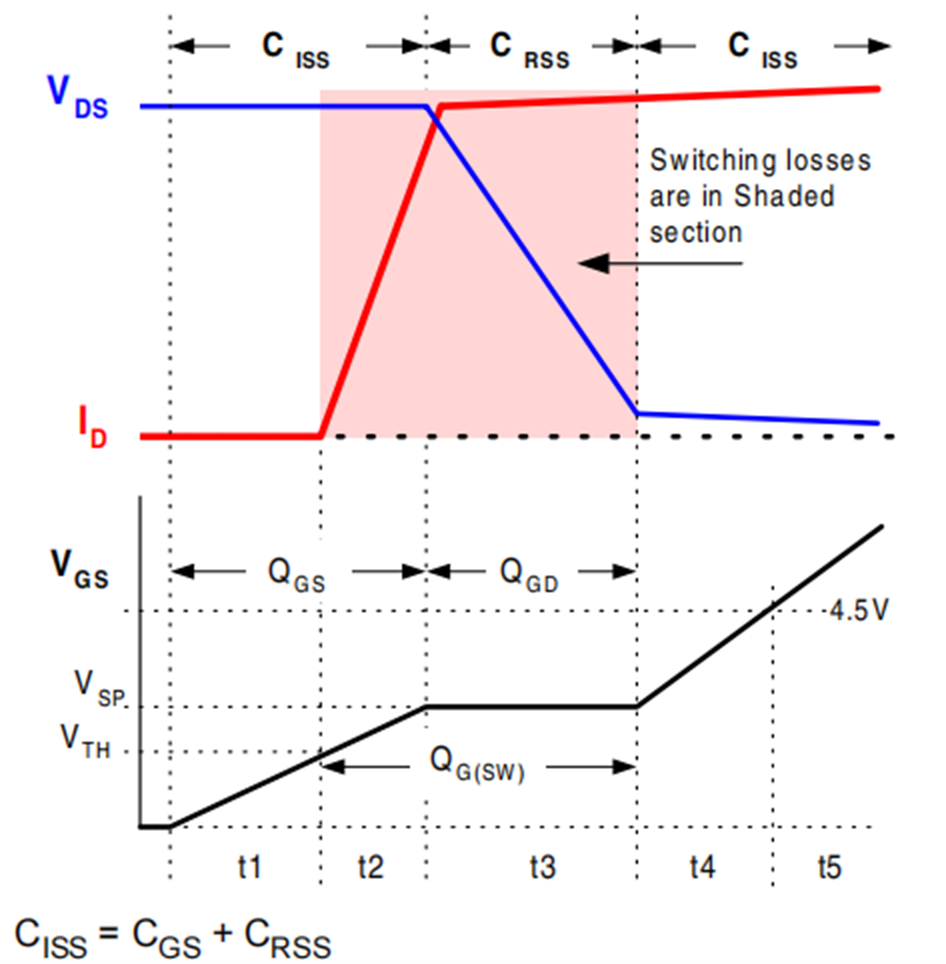
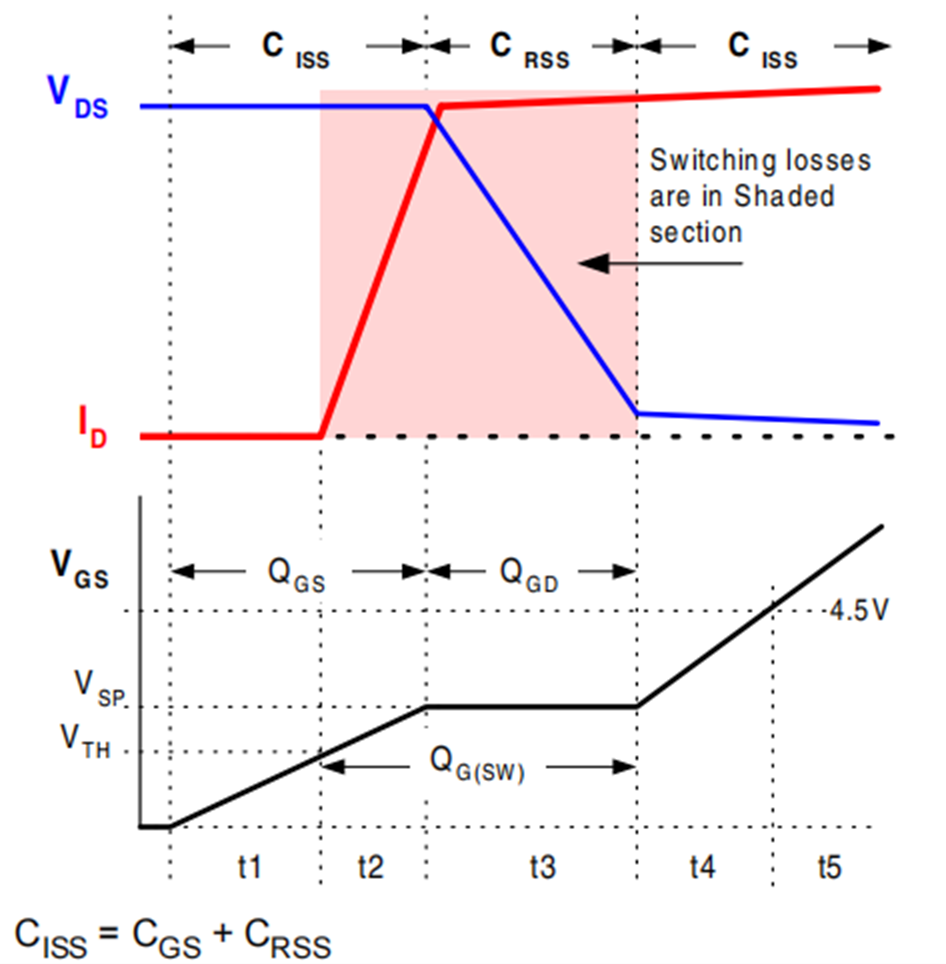
上圖中的階段③和理論曲線所展示的平臺階段趨勢基本一致：Vgs保持不變，Id也保持不變。理論曲線在前面文章中已提到過，如下圖所示。

定量計算

關于感性負載的各階段定量關系計算，基本和《MOS管的米勒效應(6)--阻性負載》講過的定量關系類似，這里不再重復。需要特別說明階段③，此時Vds和Id的變化已不同步，在阻性負載中所提到的歐姆定律關系式已不能說明問題，內部涉及電壓和電流的波形能量轉換，開關管和續流二極管的換流。

好在此時的Vgs不變，Id也不變，階段③Vgs和Id的定量計算可以和階段②在t2時刻（階段②和階段③臨界點）定量計算的結果保持相等。Vds的計算非常復雜，我們就放過自己吧……

差異點的可能解釋

細心的同學發現階段②，在仿真波形中有一個明顯的尖峰，而理論曲線沒有。基于個人理解，我這邊嘗試進行如下解釋，可能未必恰當。如有不對，還請指正。

①可能由于仿真模型搭建上有差異。理論曲線中搭建模型中使用的是恒流源，而我仿真模型中使用的是電感。

②理論曲線的仿真模型中所使用的器件是否為理想模型，我不確定。TINA-TI中的模型，確定不是理想模型。

（我自認為這個解釋不夠嚴謹…）

感性負載與阻性負載對比

我們把感性負載和阻性負載的米勒效應波形一起看下，如下圖：

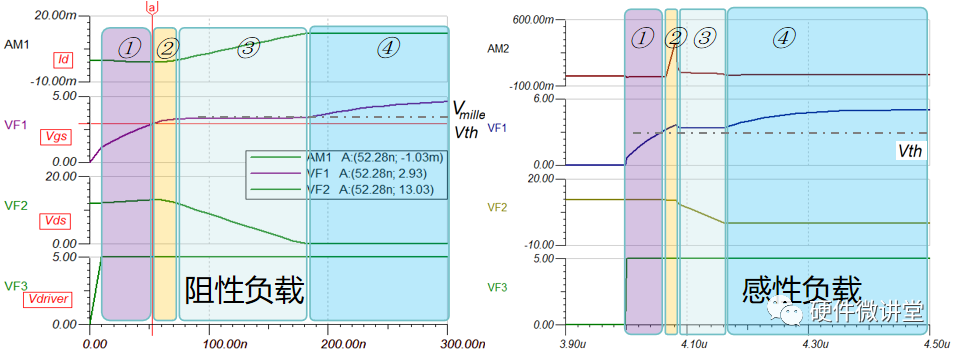
具體的差異點都在圖上，我不展開講。

只提一個點：感性負載時，在階段②，漏極電流Id在變化時，漏源電壓Vds不變；在階段③，Id不變化時，Vds在變化。

想想為什么？

感興趣的同學自己花點精力研究，我這邊點到為止。歡迎評論區留言，說出你的觀點。

總 結

先聊到這里，梳理下今天討論的內容：

①搭建感性負載的米勒效應仿真模型；

②對感性負載的米勒效應4個階段進行簡要分析；

③定量計算；

④指出仿真結果與理論曲線的明顯差異點；

⑤對比感性負載和阻性負載的米勒效應曲線，特別拋出一個問題點；

怎么樣？一個簡短的問題，給出的回答可淺可深。我的助攻只能到這里，能否晉升到陸地神仙境，一劍開天門，就看你的造化了！

審核編輯：湯梓紅