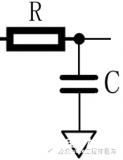
在考慮電容初始電壓之后,用于PWM濾波的二階RC低通濾波電路在頻域的等效電路如下,
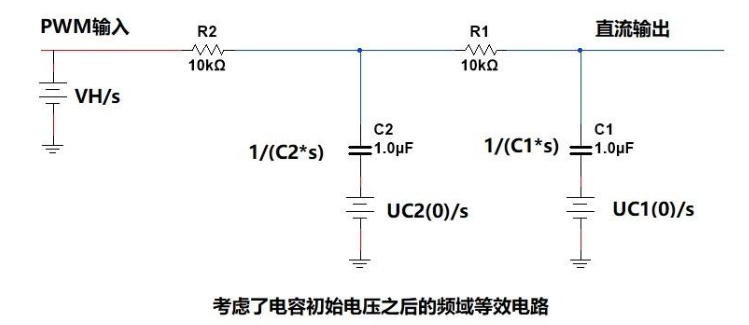
二階RC低通濾波電路
線性電路中,若含有多個獨立電源,它們共同作用在某一支路中產生的電壓或電流,必定等于各獨立電源單獨作用產生的電壓或電流的代數和,這一定理稱為疊加定理。
1)對于電壓源而言,電壓/電動勢為0,就相當于短路。
2)對于電流源而言,電流為0,就相當于開路。
第一部分
PWM輸入電源非0,而UC2(0)、UC1(0)為0,等效電路為:
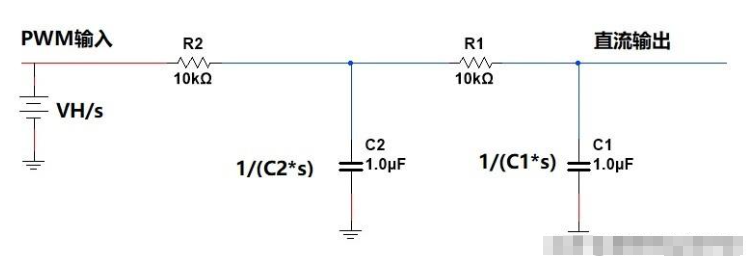
第一部分電壓
syms R2 R1 C2 C1 s VH
ZC1=1/(C1*s);%電容C1的阻抗
ZC2=1/(C2*s);%電容C2的阻抗
Z1=R1+ZC1;%Z1為R1與C1串聯
Z2=ZC2*Z1/(ZC2+Z1);%Z2為C2與Z1并聯
Vo=VH/s*Z2/(Z2+R2)*ZC1/Z1;%C1兩端的電壓為Z2與R2分壓之后,再由C1與R1分壓
simplify(Vo)%化簡符號表達式
利用octave的符號運算,得到電容C1兩端的電壓為:

第二部分
UC2(0)非0,PWM輸入電源為0,UC1(0)為0,等效電路為:

第二部分電壓
syms R2 R1 C2 C1 s VH UC20
ZC1=1/(C1*s);%電容C1的阻抗
ZC2=1/(C2*s);%電容C2的阻抗
Z1=R1+ZC1;%Z1為R1與C1串聯
Z2=R2*Z1/(R2+Z1);%Z2為R2與Z1并聯
Vo=UC20/s*Z2/(Z2+ZC2)*ZC1/Z1;%C1兩端的電壓為Z2與C2分壓之后,再由C1與R1分壓
simplify(Vo)%化簡符號表達式
利用octave的符號運算,得到電容C1兩端的電壓為:

第三部分
UC1(0)非0,PWM輸入電源為0,UC2(0)為0,等效電路為:
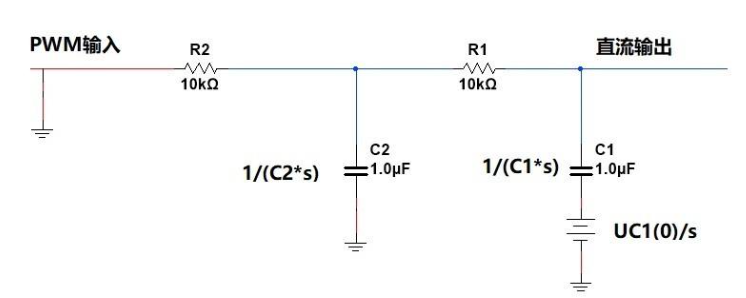
第三部分電壓
syms R2 R1 C2 C1 s VH UC10
ZC1=1/(C1*s);%電容C1的阻抗
ZC2=1/(C2*s);%電容C2的阻抗
Z1=R2*ZC2/(R2+ZC2);%Z1為R2與C2并聯
Z2=Z1+R1;%Z2為Z1,R1串聯
Vo=UC10/s/(Z2+ZC1)*Z2;%Vo為UC10 Z2與C1在Z2上的分壓
simplify(Vo)%化簡符號表達式
利用octave的符號運算,得到電容C1兩端的電壓為:

電容C1兩端的電壓為這三部分電壓相加,即:


其中,


假設 分別為方程
分別為方程
 的兩個根,則
的兩個根,則



對上式做拉普拉斯逆變換,得到:



用泰勒公式展開,并保存至t的二次項,得到:





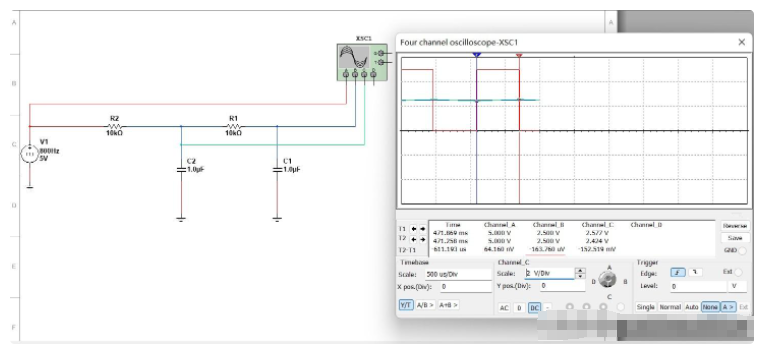
如果PWM的頻率為800Hz,占空比為50%,高電平電壓為5.0V,
R1=R2=10kΩ,C1=C2=1uF;
持續輸出一段時間,C1、C2處于穩壓,在PWM從低電平跳變到高電平的瞬間:
上式中

當t=0.625ms時,得到最大的紋波,為:

這與仿真測得的結果一致。
-
電容
+關注
關注
100文章
6090瀏覽量
150768 -
PWM
+關注
關注
114文章
5197瀏覽量
214528 -
濾波電路
+關注
關注
46文章
639瀏覽量
69773 -
RC
+關注
關注
0文章
228瀏覽量
48910 -
等效電路
+關注
關注
6文章
292瀏覽量
32805
發布評論請先 登錄
相關推薦
配置TLV320AiC3xxx系列中數字雙二階濾波器的系數





 用于PWM濾波的二階RC低通濾波電路詳解
用于PWM濾波的二階RC低通濾波電路詳解










評論