PWM開關建模CCM模式
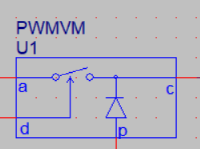
主動節點a,被動節點p,公共節點c。
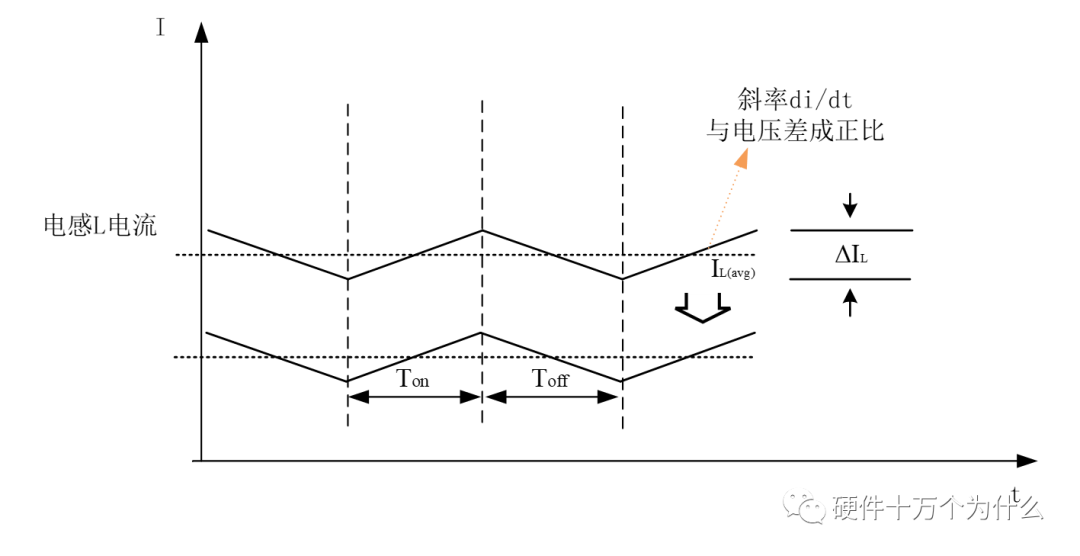
端電流不變:接入電感的公共節點電流連續為Ic,而Ia=dIc,Ip=d’Ic。
端電壓關系:ap兩端電壓始終為直流,而cp兩端電壓為ap的取樣:Vcp=dVap。
建模結果可以用直流變壓器仿真,如下
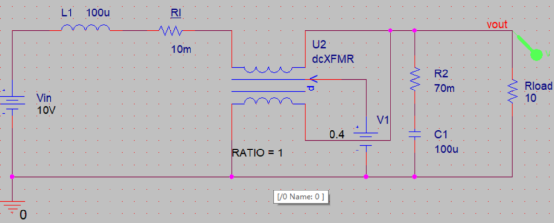
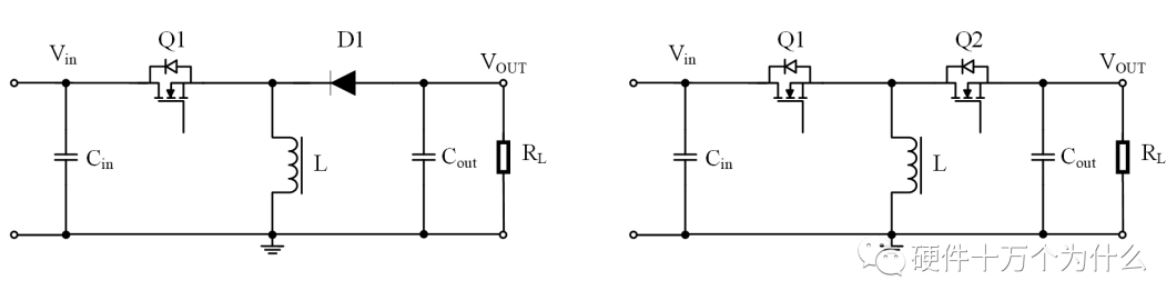
變壓器控制端朝下時,左邊為a,右邊為c,p端是下方兩個端口相連。 上圖為Boost變換器大信號仿真,直流增益受電感串聯的電阻影響的圖形為
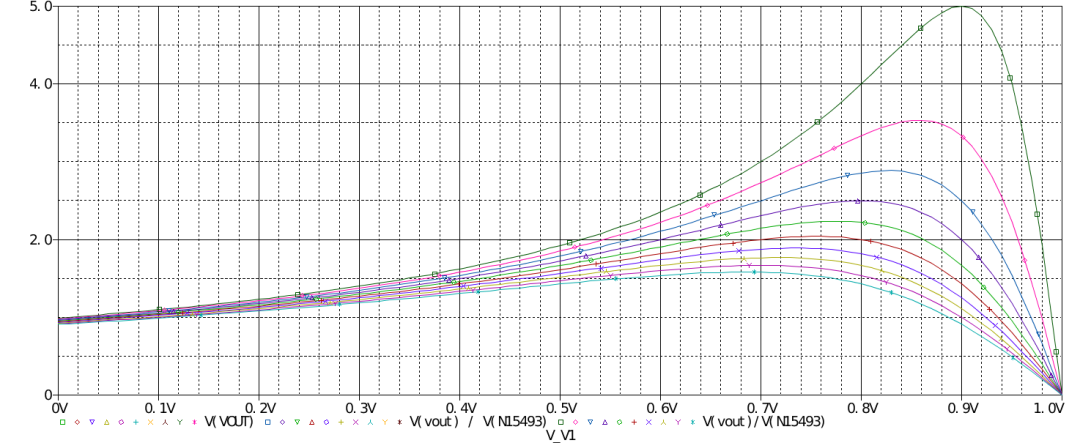
從上到下依次為100mΩ至1Ω,電感電阻對Boost的增益限制還是很大的。
也可以作小信號仿真,如下
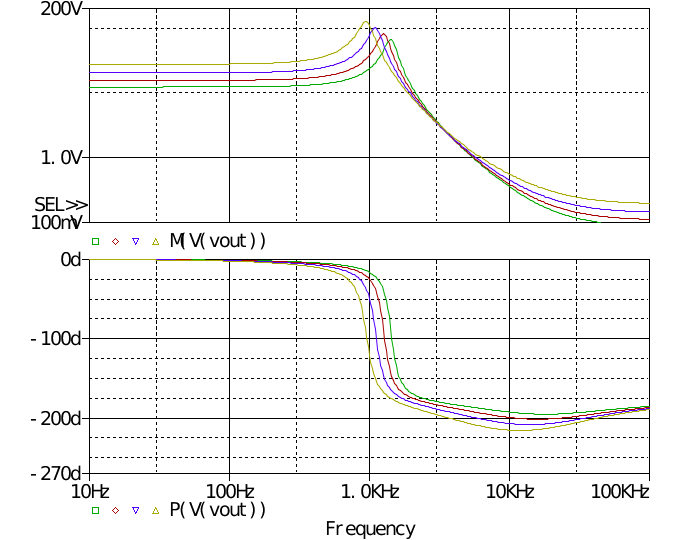
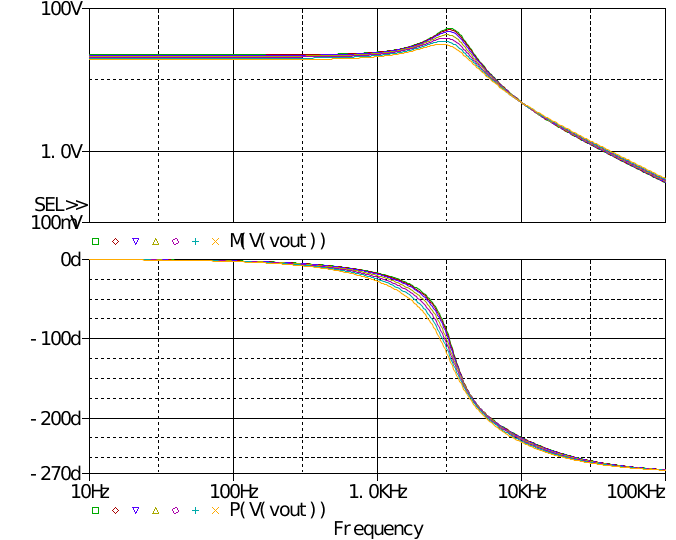
從上到下依次為D的直流量為0.4 0.3 0.2 0.1。 圖中可看出RHPZ的影響,相位裕度為負幾十度。 最后相位上揚的原因是ESR零點。
當然直接應用于帶參數掃描的小信號分析,不利于直流工作點的穩定,于是改進模型,使輸出電壓穩態值穩定于常值,即引入直流反饋,其截止頻率極低。 得到電感電阻變化時的響應曲線
PWM開關建模DCM模式
回到三端開關,DCM模式下端電流關系有一定變化:
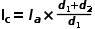
,端電壓關系也變為:
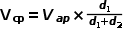
,則變壓器的匝比由d變為
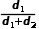
。
d~2通過峰值電流和伏秒積的關系得到,通過關系式的封裝和與CCM之間切換機制的確定,構建了一個適用于兩種情況下的仿真模型。
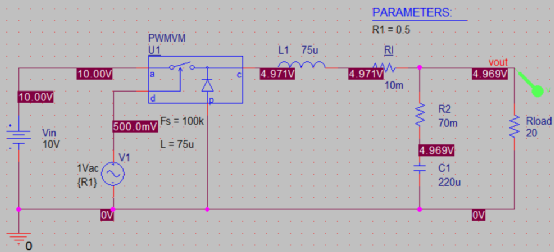
注意,該模型專為Buck使用,需要手動輸入開關頻率和外部電感值,以計算何時是臨界導通模式,才能在CCM和DCM模式之間切換。
在D=0.5下進行交流掃描,如圖電感為75uH和開關頻率為100k,算出臨界電流為0.166A。 分別把Rload設置為50Ω和5Ω,得到動態響應曲線
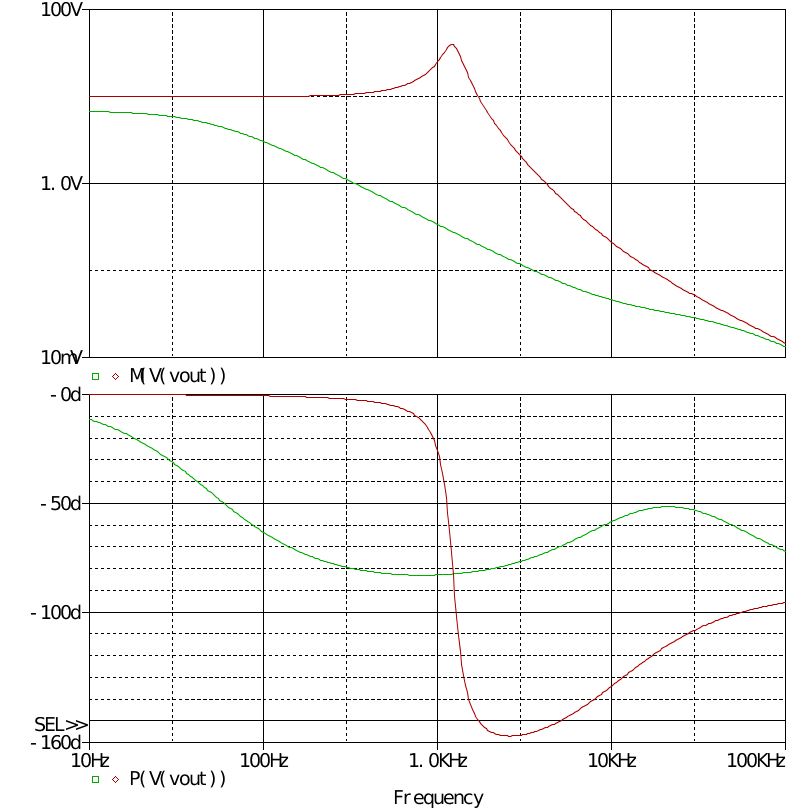
很明顯,進入DCM后由二階系統變為一階。 電路不帶有電壓反饋,輸出電壓隨負載的變化較大,因此可以同樣引入直流反饋
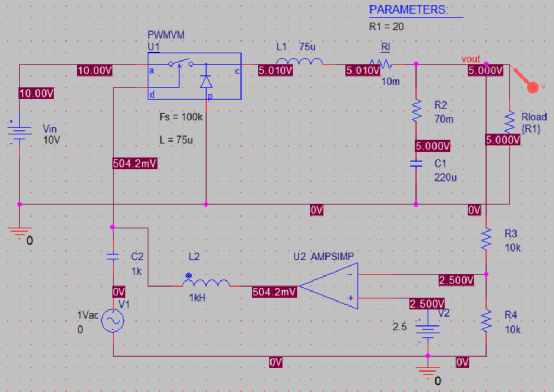
同樣作CCM和DCM下的交流分析
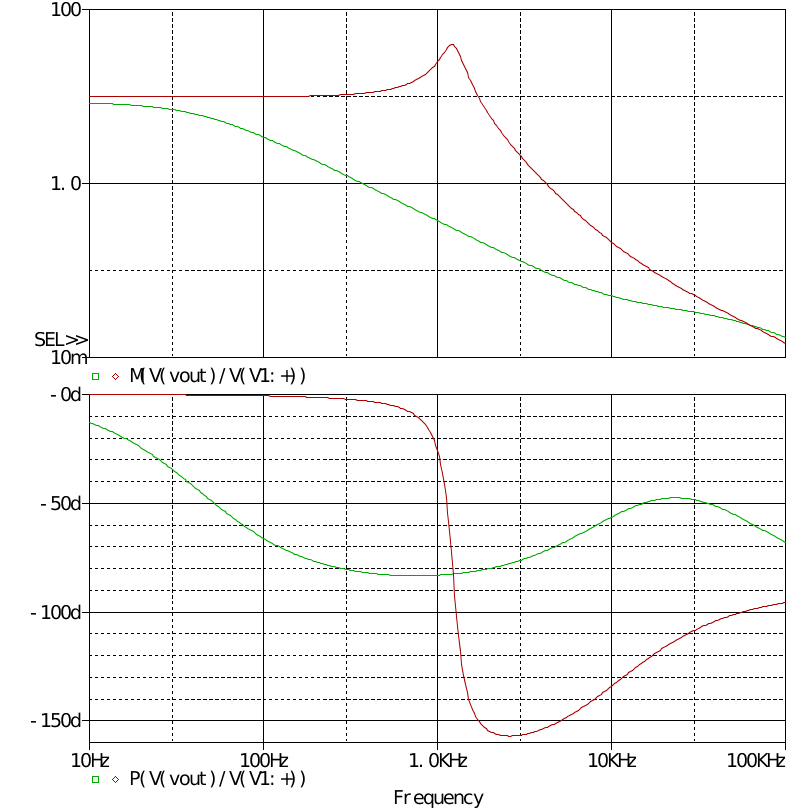
PWM調制器
已經知道,小信號模型中PWM調制器產生的增益為鋸齒波幅值的倒數。
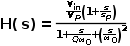
可見輸入電壓的變化會引起模型變化,影響動態響應。 若能消除輸入電壓的影響,可以令
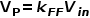
通過引入前饋增益就可以消除輸入電壓的影響。 壓控鋸齒波發生器的設計這里不贅述。 仿真時也只需在控制電壓后插入一個增益為V-~P的ABM源就可以。
系統時域響應測試
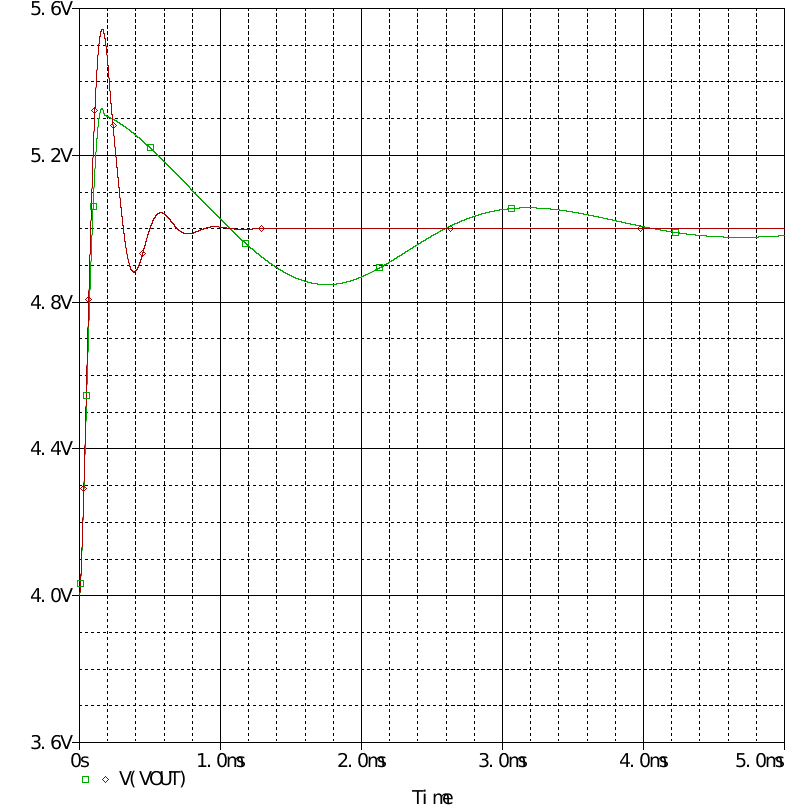
搭建一個三型補償器,同樣在CCM和DCM模式下分別進行測試,當參考電壓從2V階躍至2.5V時,輸出電壓由4V變為5V的過程
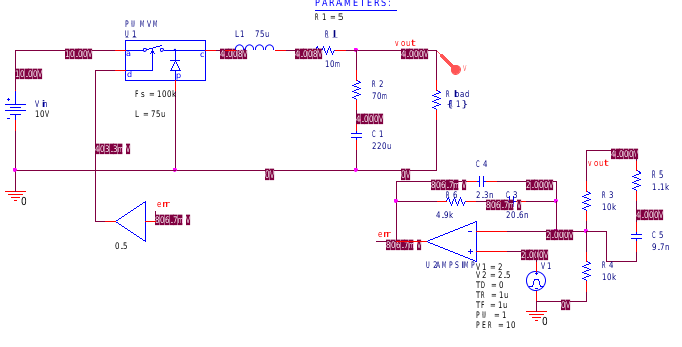
由于補償器基于CCM模式設計,因此也無法說明太多問題。 可以看到超調量還是略大的。 對補償器進行交流掃描
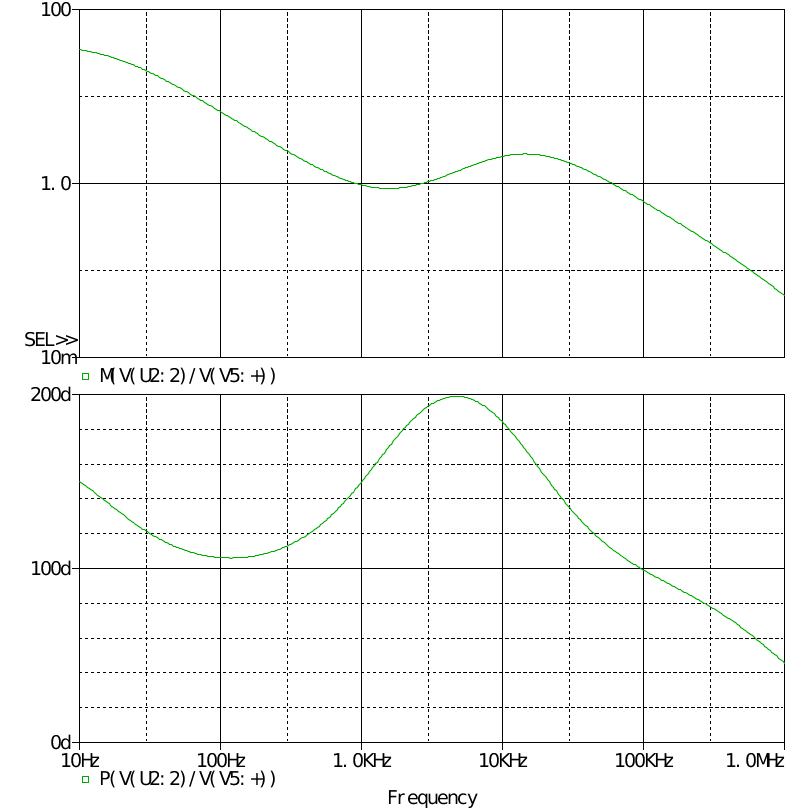
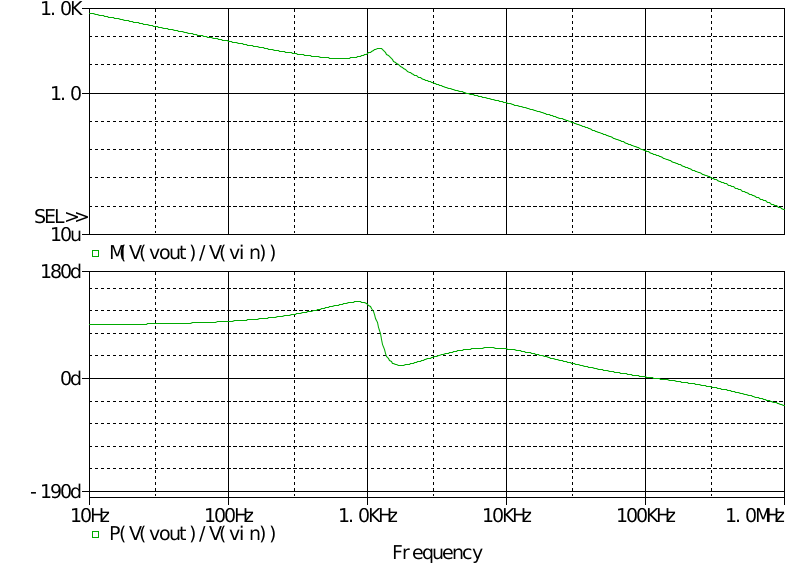
可見CCM下設計的補償器不適用于DCM模式,在設計時造成一些麻煩。
電流模式控制
CCM下的電流模式控制占空比大于0.5時需引入斜坡補償。 在推導電流模式控制的仿真模型時,因為控制效果與電壓控制模式并無本質區別,因此PWM開關也可以沿用,即電流電壓關系為
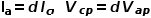
由斜坡補償的電感電流波形,求出c端的平均電流
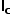
。
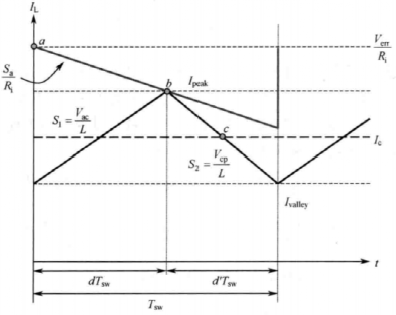
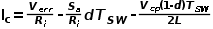
若對該表達式引入時變并求以端口電壓為變量的偏導數,得到一個小信號模型,復雜就略去了。 經過推導,發現模型中存在一個等效的諧振電容,會與電感一起產生諧振以至于產生振蕩,這或許就是次諧波振蕩的來源。 計算品質因數與補償斜率的關系后,推導出令品質因數為1以下時的補償斜率
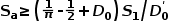
D~0表示穩態占空比。 這是選擇補償斜率的方法之一。 或者簡單地選擇為截止時斜率的一半,前提是電路不進入BCM模式。
DCM時仍需要斜坡補償(原因沒說),因為多了一個0電流模態,可得c端電流平均值
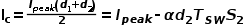
而對有斜坡補償的電流峰值為
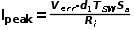
可以得到
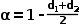
和電流平均值的表達式
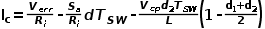
當d2=1-d1時就變成CCM模式。 通過以上式子可以得到d2等參數,從而構建一個CCM和DCM通用的仿真模型,形式上與電壓模式控制并無差異。
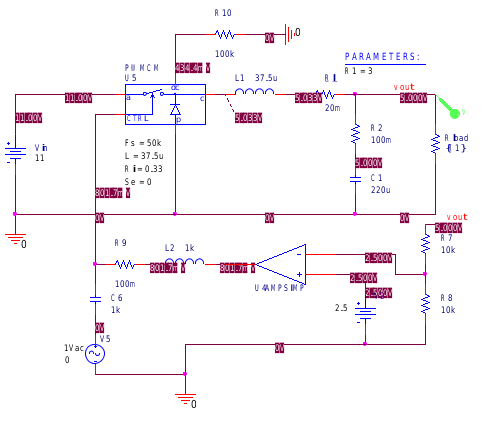
注意的是,庫中的PWMCM包含諧振電容,而PWMCMX為了避免瞬態仿真中的收斂問題,去掉了諧振電容,瞬態仿真時可以用這個模型。
與之前一致作直流閉環下的小信號仿真,先設置S ~a=0,即沒有斜坡補償的電流模式控制,得到波特圖
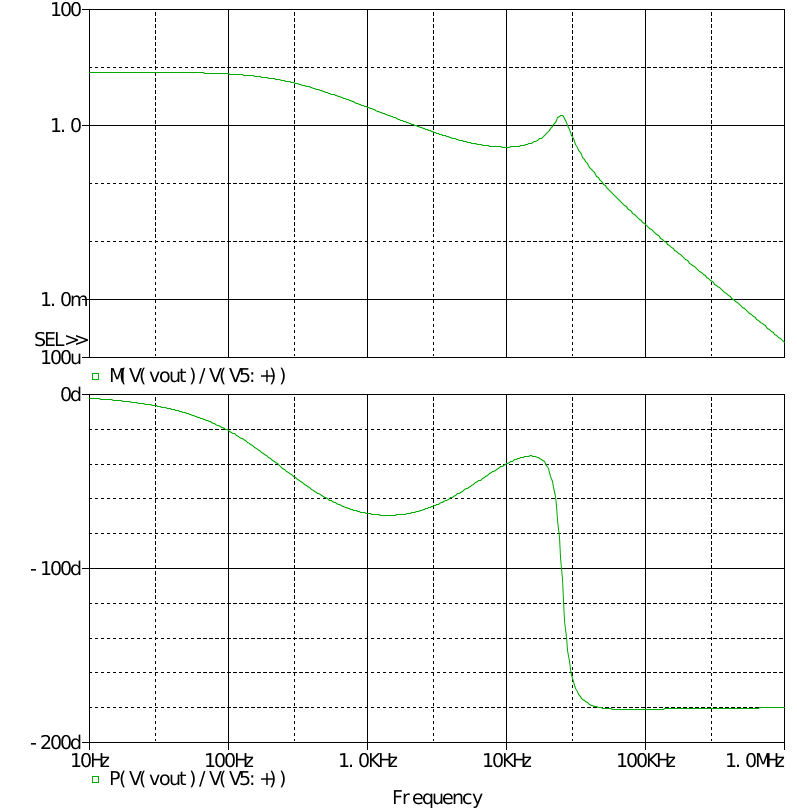
可見未補償時在高頻處存在一個諧振峰,在此例中這個諧振峰穿越了0dB線,將會影響性能,與理論預測的一致。
再進行斜坡補償,如前所述選擇補償斜率,這里電路運行于CCM模式,假定不會進入BCM,可以直接取為截止斜率(也可以是導通斜率)的一半為
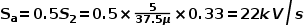
其中0.33是電流取樣電阻的阻值。 若取導通斜率的一半則為26.4kV/s。 補償后的波特圖為
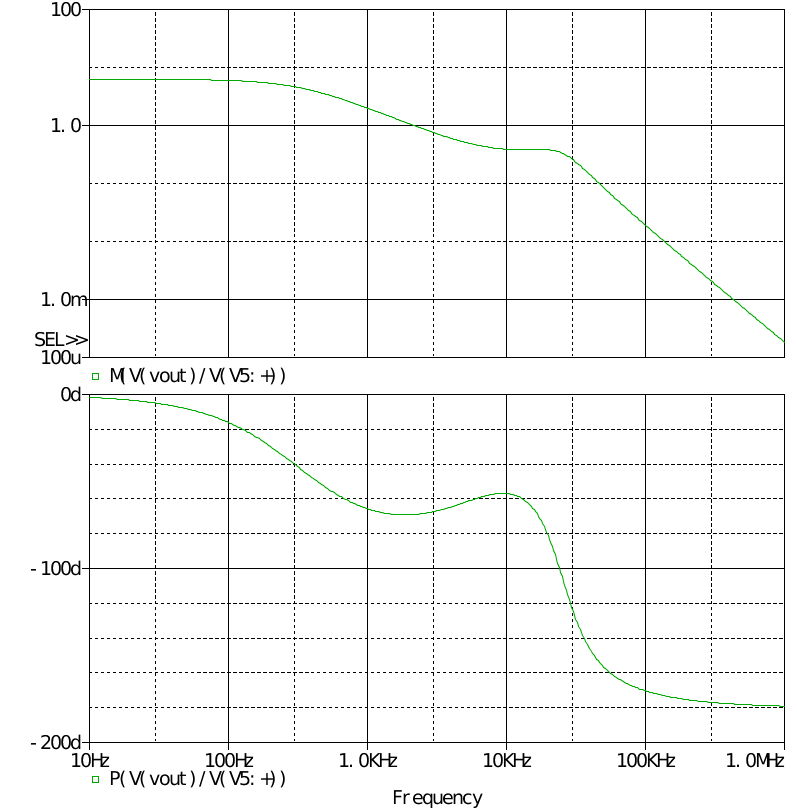
則消除了諧振峰,穩定性改善了許多。
占空比信號直接生成
一般將電壓模式控制稱為直接占空比控制,將電流模式控制稱為間接占空比控制,因為電流模式控制中多了一個誤差電壓轉化為峰值電流的環節。 通過直接推導占空比的表達式然后構建模型,理論上可以實現,但CCM下的模型似乎并不能預測到高頻的諧振點。 DCM下的模型運行良好。
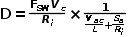
考慮寄生參數
紋波電流在輸入電容和輸出電容存在的ESR上形成紋波電壓,導致PWM開關模型的
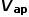
和
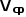
并非恒定值,而是疊加了一個紋波。 如果把寄生參數考慮進PWM開關中,可以直接構建一個
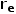
,隨拓撲的變化而變化。 由端電壓關系有
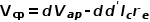
即在p端加入一個阻值為
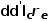
的電阻。
再考慮MOS管導通電阻和二極管導通壓降的影響。 流經MOS和二極管的電流不變,而且在PWM開關中已經定義好了分別是a端和p端,那么最終變化的也是電壓波形。
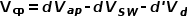
后兩項可以用兩個電壓源實現,但開關SW和二極管的具體壓降由流經的電流和選擇的器件參數決定,這時就需要外接實際的管子,然后PWM開關模型再通過管子上的實際壓降來計算得出模型參數。
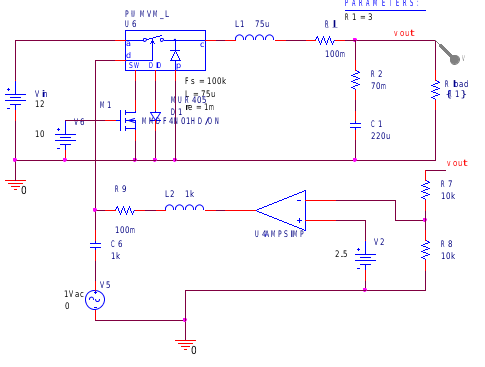
注意的是外接MOS管和二極管的實質是測量其上的導通電壓,而不是讓它們參與變換器的工作,因此MOS管直接用一個直流電源維持導通,二極管也直接陰極接地,維持導通。
電流模式下的模型也如上所述。
這些損耗模型因為是利用電流平均值生成損耗電壓值,而實際中損耗能量是與電流有效值有關,其差別有時不可忽略,所以精確性并非最佳。
邊界導通模式的PWM模型
頻率變化的BCM具有特別的優點:避免反向恢復的影響; 電路模型退化成一階; 易于實現軟開關。 其控制思想就是讓電感電流到0時就打開開關管。 用于反激拓撲中稱為準諧振拓撲,若利用關斷振鈴插入延遲,則可以實現軟開關。
BCM下,端電流恰為峰值的一半
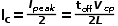
模型以導通時間

為輸入參數。
四階變換器Cuk電路例子
同樣用書中給出的PWM開關模型可以構建其他拓撲,Cuk電路及其交流響應如下
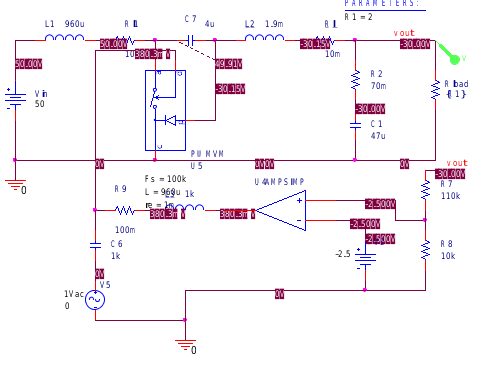
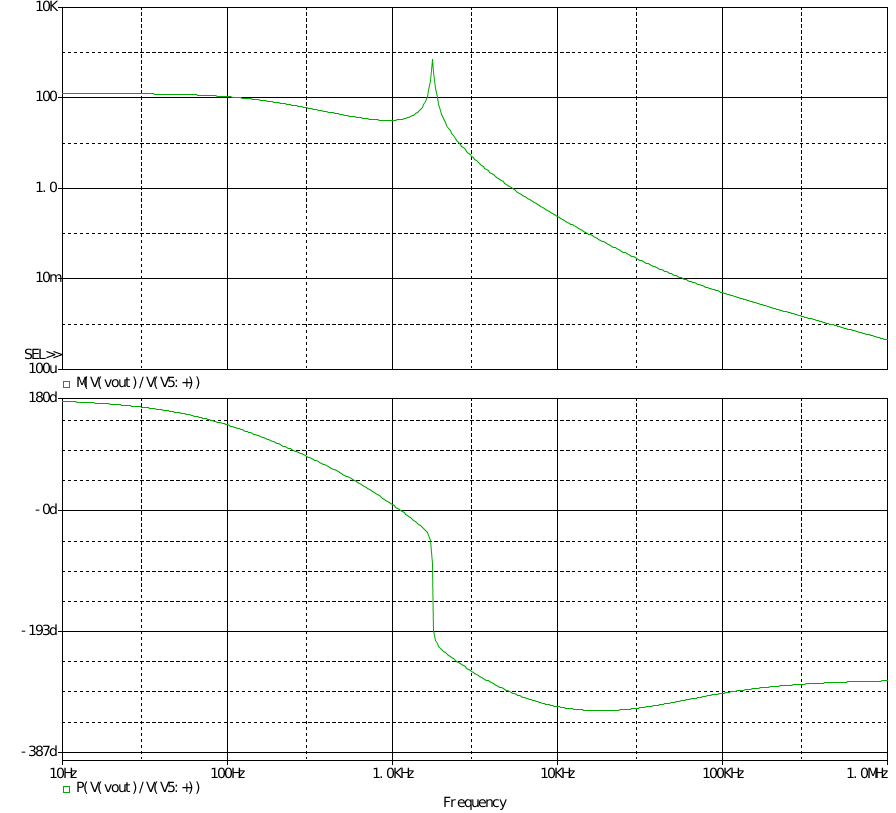
明顯可以看出相移達到-320°,確是四階系統,后面因ESR零點略有上升。 在截止頻率處相移為-290°,相位裕度為-110°,極易振蕩。 以下是在占空比輸入階躍信號時的輸出響應。
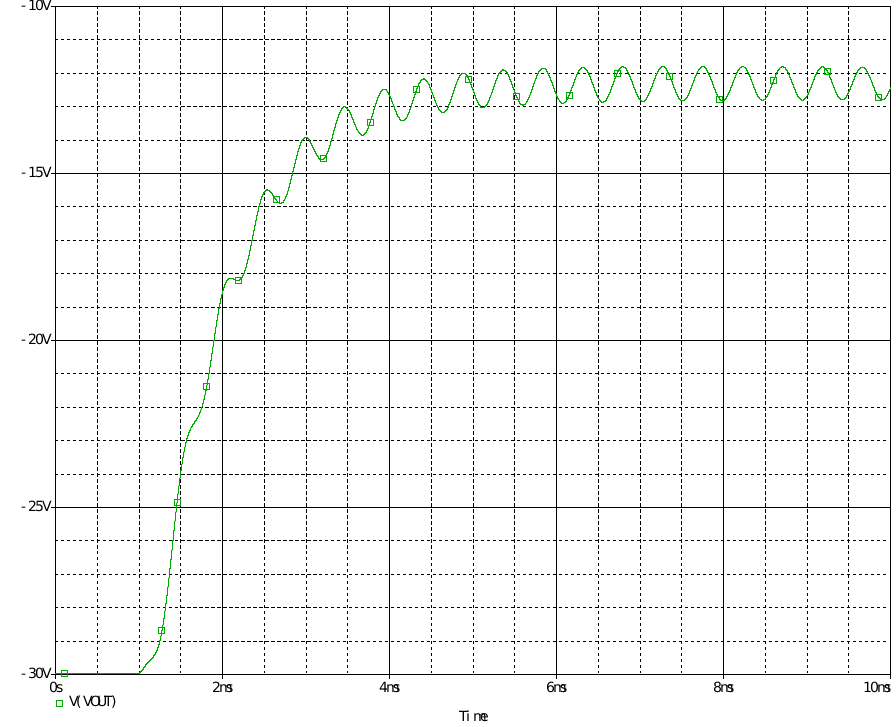
而下圖是把閉環的參考電壓換成階躍電壓源,得出發散振蕩的結果
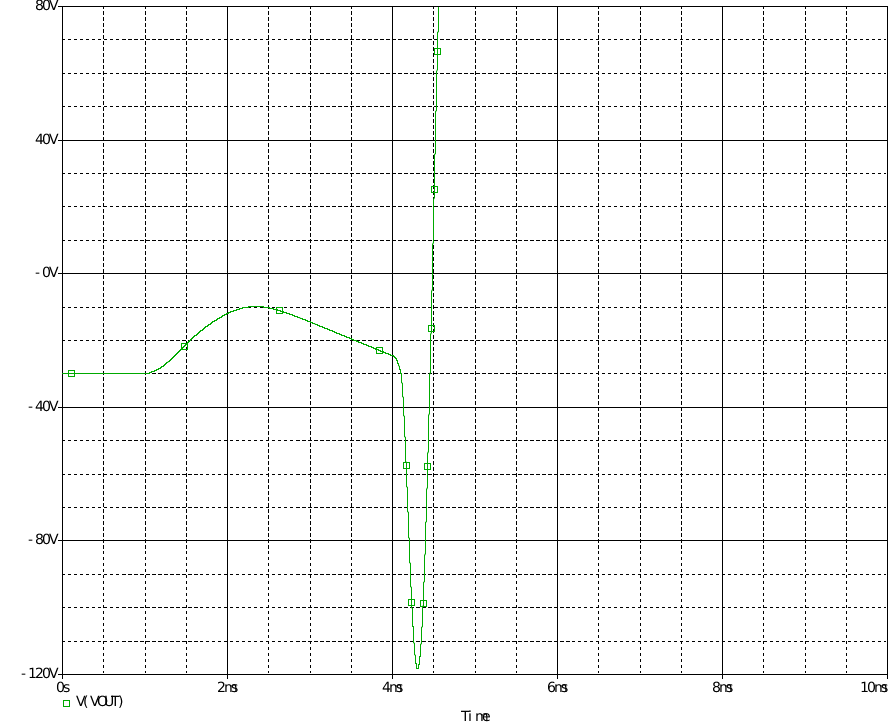
-
開關
+關注
關注
19文章
3144瀏覽量
93815 -
PWM
+關注
關注
114文章
5197瀏覽量
214528 -
電壓
+關注
關注
45文章
5636瀏覽量
116103 -
DCM
+關注
關注
0文章
160瀏覽量
26532 -
CCM
+關注
關注
0文章
146瀏覽量
24072
發布評論請先 登錄
相關推薦
開關電源Buck電路CCM及DCM工作模式

開關電源Buck電路CCM與DCM工作模式有什么區別?

開關電源Buck電路CCM和DCM工作模式





 PWM開關建模CCM和DCM模式講解
PWM開關建模CCM和DCM模式講解










評論