本文您將了解到史密斯圓圖的歷史和來龍去脈,以及它與反射系數的關系及如何使計算阻抗更容易。
史密斯圓圖是一種圖形化的 RF 設計工具,它使我們能夠輕松計算將給定阻抗轉換為另一個阻抗所需的阻抗匹配網絡的組件。
早在 1930 年代,史密斯圓圖就是高頻工作的主要內容。對于今天的計算機,這種圖形工具作為計算輔助工具可能已經變得不那么重要了;但是,它仍然是直觀地可視化RF電路不同參數的有用工具。如此之多,以至于所有射頻電路和系統模擬器以及測量設備(如網絡分析儀)都可以直接在史密斯圓圖上顯示其輸出。考慮到其廣泛使用,有必要對史密斯圓圖有透徹的了解,以便能夠使用不同的射頻模擬器和測量設備。
史密斯圓圖對于通過手工計算設計阻抗匹配網絡也非常有用。使用史密斯圓圖設計阻抗匹配網絡快速、直觀,而且在實踐中通常足夠準確。
史密斯圓圖上的反射系數:一個表現良好的參數
史密斯圓圖基本上是反射系數的極坐標圖(以及我們稍后將介紹的一些其他圖)。考慮到史密斯圓圖的廣泛流通,您可能會正確地猜到反射系數參數在基于 RF 的工作中是最重要的。使用低頻電路的模擬設計師通常使用阻抗概念來分析和建模他們的電路。當頻率超過幾百兆赫茲時,阻抗的概念就有些失去用處了。在更高頻率下,反射系數的概念可能更有幫助。
為了更好地理解反射系數的獨特特征,請參考圖1中的圖表,該圖顯示了一條以任意阻抗Z L.為終端的傳輸線。
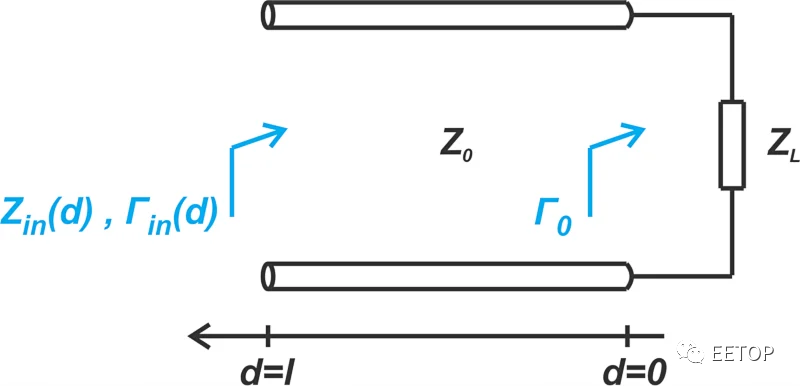
圖 1.傳輸線端接任意阻抗。
傳輸線沿線不同點的輸入阻抗通過公式 1 給出:
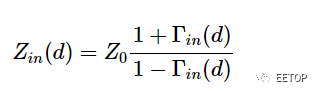
等式 1
其中 (d)中的Γ,距離負載 d 處的反射系數,如等式 2 所示:
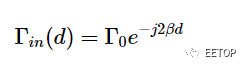
等式 2
在公式 2 中,β 是相位常數,Γ0是熟悉的負載反射系數,由此得出等式 3:
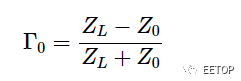
等式 3
等式 3 很容易理解;它給出了給定ZL的負載反射系數。例如,如果 ZL= 50 + j50 Ω 和Z0= 50 Ω,我們得到 Γ0= 0.2 + j0.4。等式 2 顯示了反射系數如何沿線變化。如您所見, (d)中Γ 的大小是恒定的,等于 Γ0的大小(上述值為0.447);然而,它的相位角隨與負載的距離線性變化。
例如,如果βd(稱為線路的電氣長度)為45°,則(d)中Γ的相位角為Γ0的相位減去90°(63.4°- 90° = -26.6°)。圖 2 中的以下極坐標圖顯示了如何從 Γ0以圖形方式獲得 (d)中的Γ。
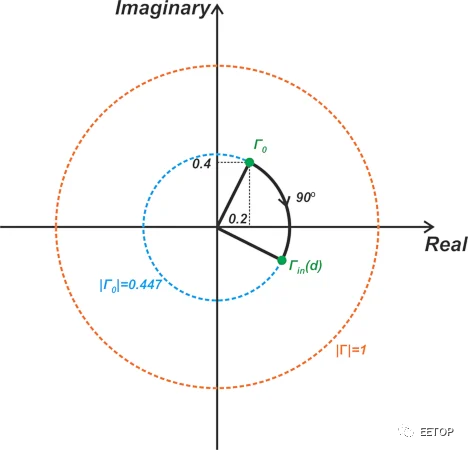
圖 2. 使用上述示例和方程式的示例極坐標圖。
可以看出,對于給定的Γ0,(d)中沿線Γ的反射系數位于半徑為|Γ0|的圓上。總而言之,反射系數是一個性能良好的 RF 參數,因為它的幅度沿線路恒定,并且其相位角隨線路長度線性變化。線路阻抗不是這種情況。對于不匹配的負載,輸入阻抗沿線路連續變化。對于 |Γ0|= 1,輸入阻抗的大小可以在零和無窮大之間的任何地方。
高頻反射系數——測量的簡便性和可靠性
反射系數在高頻工作中是一個更具吸引力的參數還有另一個原因。阻抗的概念很自然地將我們引向二端口網絡表示,例如阻抗參數、導納參數和混合參數。為了通過實驗確定這些表示的參數,我們需要開路或短路適當的網絡端口。然而,在高頻下,很難提供短路和開路條件,尤其是在很寬的頻率范圍內。此外,有源高頻電路在開路或短路時可能會振蕩。
另一方面,反射系數的概念與S參數表示密切相關。使用這種類型的網絡表示,網絡的適當端口終止于線路的特性阻抗。例如,下圖(圖 3)測量了兩個 S 參數,即 S11(輸入反射系數)和S21(從端口 1 到端口 2 的傳輸系數)。
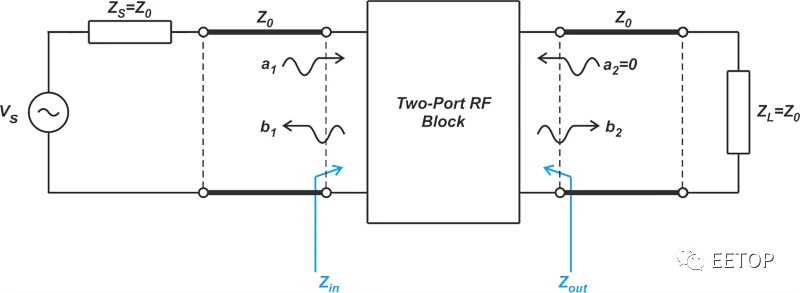
圖 3. 顯示兩個 S 參數的示例圖。
與其他類型的網絡表示相比,S 參數的一大優勢是 S 參數測量所需的寬帶電阻終端在實踐中是可以實現的。這使我們能夠進行準確且可重復的射頻測量。
史密斯圓圖的發明
AT&T 工程師Philip Smith 于 1933 年發明了 Smith 圓圖,以簡化傳輸線的輸入阻抗計算。如上所述,史密斯圓圖是反射系數的極坐標圖。然而,在那些日子里,工程師們習慣于使用阻抗概念。反射系數的圖表對他們來說沒有多大意義。
首先,我們設置一些背景來了解史密斯發明的重要性。S 參數由 K.Kurokawa 在 1960 年代引入。在史密斯圓圖發明 30 多年后的1960 年代,還引入了使用 S 參數將 RF 組件表征為千兆赫區域的網絡分析儀。Smith 至少已經認識到反射系數相對于阻抗的一些優勢,并決定使用 Γ 概念來解決他所涉及的問題。為了能夠用熟悉的阻抗參數術語與其他工程師交談,Smith還決定包括一些阻抗圖,以便可以輕松找到給定反射系數的等效阻抗,反之亦然。通過繪制 Γ 平面中恒定電阻和電抗的等值線,
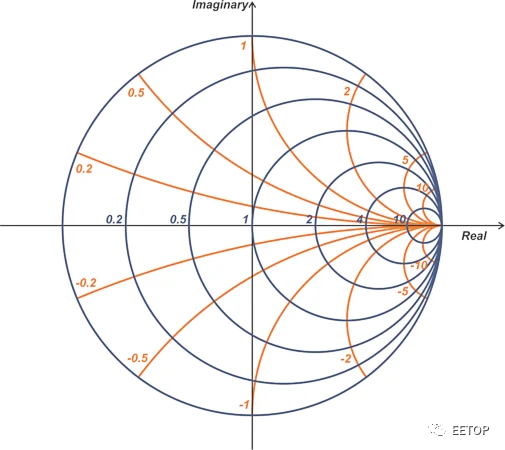
圖 4. 史密斯圓圖示例。
在大多數 Smith 圓圖中,Γ 平面的實軸和虛軸沒有顯示,因為實際上沒有必要明確顯示它們。這給我們留下了一些分別對應于恒定電阻和電抗等值線的圓和弧。讓我們看看這些偶爾會變得令人生畏和困惑的等高線是如何獲得的,以及我們如何解釋它們。
史密斯圓圖歸一化阻抗
史密斯圓圖基于Γ0和阻抗之間的關系(等式3)。請務必注意,等式3 描述了這兩個參數之間的一對一關系,因此知道一個就等同于知道另一個。此外,史密斯圓圖是使用歸一化阻抗繪制的,定義如下:
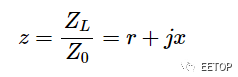
等式 4
其中 r 和 x 是歸一化阻抗的實部和虛部。繪制歸一化阻抗允許我們對具有不同參考阻抗的系統使用相同的圖表。但是,我們需要記住,我們從圖表中讀取的阻抗應該乘以Z0才能找到我們系統的實際阻抗值。另請注意,使用歸一化阻抗不會改變 Γ0方程。為了用歸一化阻抗表示 Γ0,我們將等式 3 的分子和分母都除以 Z0 ,這顯然不會改變等式。根據 z 的Γ0方程如下所示:
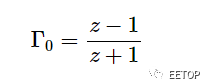
等式 5
因此,雖然史密斯圓圖上顯示的阻抗已歸一化,但反射系數并未歸一化。等式 5 是確定給定 z 如何產生其對應 Γ 的映射函數。這個方程實際上是一個雙線性變換。這個名字源于它是兩個線性函數的比率。雙線性變換將圓映射為圓。請記住,對于數學家來說,直線也是圓的特例。
恒阻圓
作為雙線性變換,等式 5 將常數 r 的線(或具有常數實部的阻抗)映射到 Γ 平面中的圓。例如,直線 z = 0 + jx 被轉換為以 Γ 平面原點為中心、半徑為 1 的圓(請參見下方圖 5 中的藍線和藍圈)。
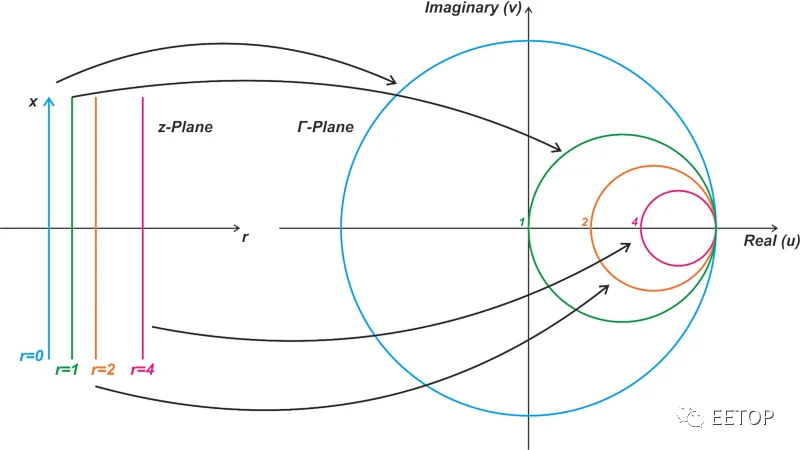
圖 5. 雙線性變換示例。
類似地,變換將線 z = 1 + jx 映射到以 u = 0.5 和 v = 0 為中心的半徑為 0.5 的圓。通常,可以證明具有常數 r 的阻抗被變換為半徑為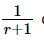 ?為中心的圓?
?為中心的圓?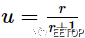 ? 并且v = 0。
? 并且v = 0。
恒電抗環
對于某些 x 值,具有恒定電抗的阻抗映射如圖 6 所示。
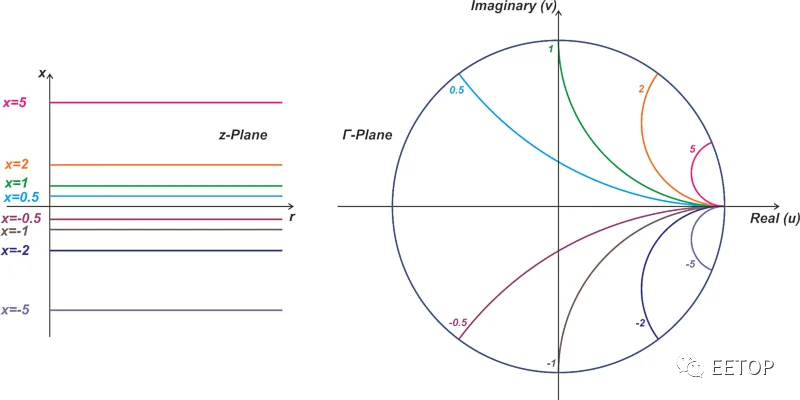
圖 6. 具有恒定電抗的阻抗映射示例。
同樣,等式 5 的雙線性變換將 x 常數(或具有常數虛部的阻抗)的線映射到 Γ 平面中的圓。請注意,上圖中僅顯示了這些圓中位于單位圓內的部分。使用無源負載時,|Γ|不能超過unity。這意味著阻抗在單位圓內具有 r ≥ 0 映射。這就是為什么我們在處理史密斯圓圖時通常對局限于單位圓的區域感興趣。只有一部分恒電抗圓落在單位圓內,因此,這些曲線表現為一些圓弧而不是完整的圓。
通常,具有常數 x 的阻抗被轉換為半徑為1/x 的圓,中心是u=1 和 v=1/x。史密斯圖是反射系數與上述恒定電阻和電抗輪廓線疊加的極坐標圖(上圖4)。
審核編輯 :李倩
-
阻抗
+關注
關注
17文章
962瀏覽量
46629 -
高頻
+關注
關注
11文章
477瀏覽量
53209 -
線性
+關注
關注
0文章
199瀏覽量
25367
原文標題:史密斯圓圖的歷史和來龍去脈,了解其與反射系數和阻抗的關系
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




















評論