1、換路定理:換路前后,電容兩端的電壓不能突變,電感中的電流不能突變,此關系稱為換路定則。
2、一階電路時域分析
(1)微分方程的建立:電路中存在單個動態元件(一個電容或一個電感)的電路稱為一階電路,常見的一般有一階RC電路和一階RL電路。如下圖所示
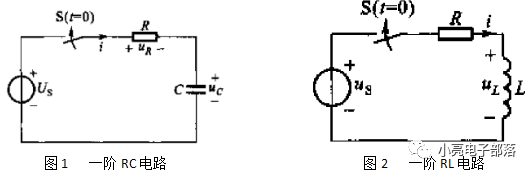
建立微分方程的步驟如下:確定電路中的中間變量(比如電流或電壓);通過中間變量確定輸入與輸出之間的參數方程,消去中間變量即可得到輸入與輸出之間的方程。
對于一階RC電路微分方程的建立步驟如下:由于電路是串聯,所以取電流i作為中間變量,輸入電壓為Us,所以根據KVL建立方程
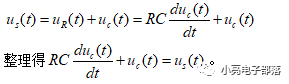
對于一階RL電路微分方程的建立步驟如下:由于電路是串聯,所以取電流i作為中間變量,輸入電壓為Us,所以根據KVL建立方程
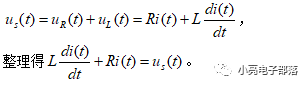
根據換路定理,一般在一階RL電路中,建立的是電感電流和電壓激勵的關系,在一階RC電路中建立的是電壓激勵和電容電壓的關系。
(2) 零輸入響應 :所謂零輸入響應就是當電路的激勵為零的時候,動態元件依靠初始儲能完成的輸出響應,對應到一階微分方程上,就是求一階微分方程的齊次解。對于一階RC電路,零輸入響應為
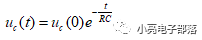
對于一階RL電路,零輸入響應為
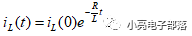
(3) 零狀態響應 :所謂零狀態響應就是當電路存在輸入激勵且動態元件的初始狀態為0的時候,動態元件依靠輸入激勵完成的輸出響應,對應到一階微分方程上,就是求一階微分方程的通解,對于一階RC電路,零狀態響應為
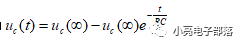
對于一階RL電路,零狀態響應為
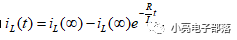
其中無窮代表的是穩態時候的值。
(4)一階系統的 全響應 :當一個電路的激勵和初始狀態均不為0的時候產生的響應稱為一階電路的全響應,全響應一般可以拆分為零輸入響應和零輸出響應的疊加,或者是穩態分量與暫態分量的疊加,所謂暫態分量就是指其幅值隨著時間趨向無窮大而趨向于0的部分。所以一階電路的全響應的求解可以采用三要素法,其中的三要素就是穩態值,初始值和時間常數,即全響應
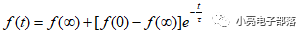
其中對于一階RC電路來說時間常數等于RC;對于一階RL電路來說時間常數等于L除以R。
3、二階電路時域分析
(1)微分方程的建立:二階系統即電路中同時存在兩個動態元件,一般是電容和電感同時存在,此時建立的方程是一個二階常系數非齊次線性微分方程,這種方程的求解通常比較復雜,因此不要求掌握,理解即可。方程的建立方式與一階系統一樣。
(2)零輸入響應
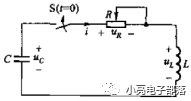
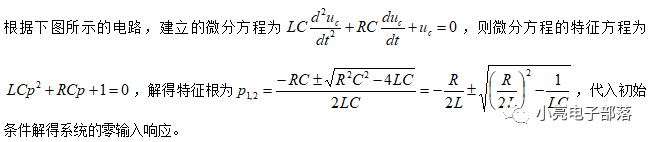
(3)零狀態響應與全響應:二階系統的零狀態響應與全響應只需要求解對應的微分方程通解即可,本部分不再贅述。
3、階躍響應與沖激響應:當輸入為階躍信號與沖激信號時系統產生的響應稱為階躍響應與沖激響應。由于一階系統和二階系統一般為LTI系統(線性時不變連續系統),所以滿足線性性質,微分性質和積分性質。


5、例題分析
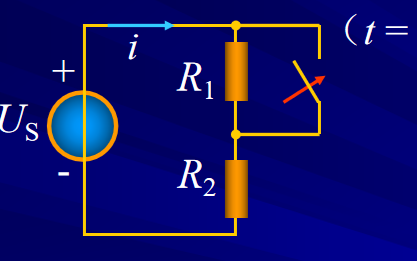
例題1:已知圖中開關在位置1處很久,當t=0時刻轉換到位置2,求換路后的電感的電流和電感兩端的電壓。
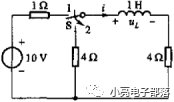

例題2:已知圖中開關在位置1處很久,當t=0時刻轉換到位置2,求換路后的100K電阻上的電流和電容兩端電壓。
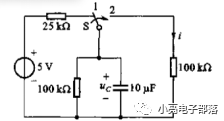

例題3:已知微分方程為
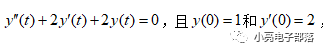
求解系統的零輸入響應。

例題4:計算
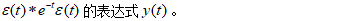
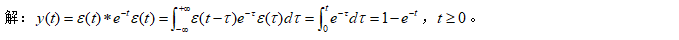
-
電路
+關注
關注
172文章
5959瀏覽量
172713 -
RC電路
+關注
關注
2文章
163瀏覽量
30311 -
RL電路
+關注
關注
0文章
7瀏覽量
6186
發布評論請先 登錄
相關推薦
第7章 一階電路和二階電路的時域分析
第7章 一階電路和二階電路的時域分析
二階有源低通濾波器_最簡單的二階低通濾波器電路圖
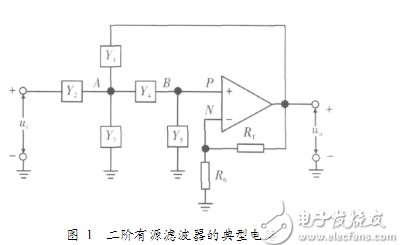




 一階電路與二階電路的時域分析
一階電路與二階電路的時域分析
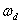











評論