有個事情可能會讓初學者驚訝:神經網絡模型并不復雜!『神經網絡』這個詞讓人覺得很高大上,但實際上神經網絡算法要比人們想象的簡單。
這篇文章完全是為新手準備的。我們會通過用Python從頭實現一個神經網絡來理解神經網絡的原理。本文的脈絡是:
- 介紹了神經網絡的基本結構——神經元;
- 在神經元中使用S型激活函數;
- 神經網絡就是連接在一起的神經元;
- 構建了一個數據集,輸入(或特征)是體重和身高,輸出(或標簽)是性別;
- 學習了損失函數和均方差損失;
- 訓練網絡就是最小化其損失;
- 用反向傳播方法計算偏導;
- 用隨機梯度下降法訓練網絡。
***01 ***磚塊:神經元
首先讓我們看看神經網絡的基本單位,神經元。神經元接受輸入,對其做一些數據操作,然后產生輸出。例如,這是一個2-輸入神經元:
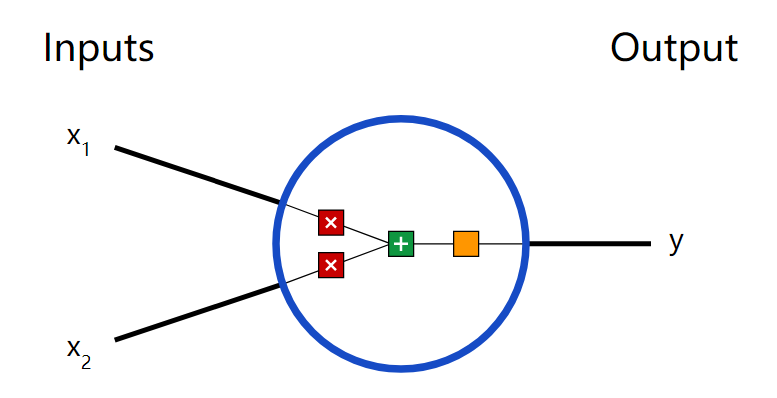
這里發生了三個事情。首先,每個輸入都跟一個權重相乘(紅色):
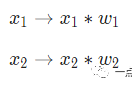
然后,加權后的輸入求和,加上一個偏差b(綠色):
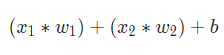
最后,這個結果傳遞給一個激活函數f:
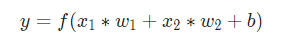
激活函數的用途是將一個無邊界的輸入,轉變成一個可預測的形式。常用的激活函數就就是S型函數:
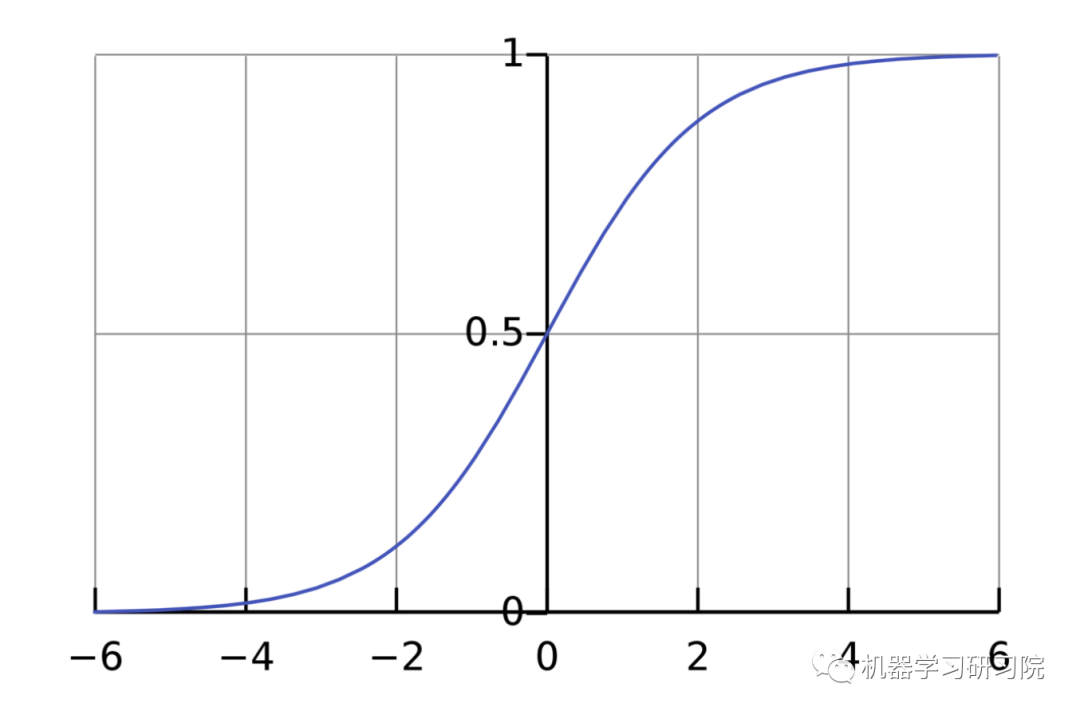
S型函數的值域是(0, 1)。簡單來說,就是把(?∞, +∞)壓縮到(0, 1) ,很大的負數約等于0,很大的正數約等于1。
***02 ***一個簡單的例子
假設我們有一個神經元,激活函數就是S型函數,其參數如下:
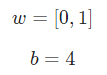
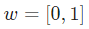 就是以向量的形式表示
就是以向量的形式表示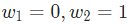 。現在,我們給這個神經元一個輸入
。現在,我們給這個神經元一個輸入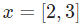 。我們用點積來表示:
。我們用點積來表示:
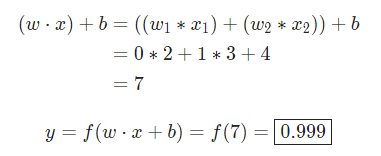
當輸入是[2, 3]時,這個神經元的輸出是0.999。給定輸入,得到輸出的過程被稱為前饋(feedforward)。
***03 ***編碼一個神經元
讓我們來實現一個神經元!用Python的NumPy庫來完成其中的數學計算:
import numpy as np
defsigmoid(x): # 我們的激活函數: f(x) = 1 / (1 + e^(-x)) return 1 / (1 + np.exp(-x))
classNeuron: def__init__(self, weights, bias): self.weights = weights self.bias = bias
deffeedforward(self, inputs): # 加權輸入,加入偏置,然后使用激活函數 total = np.dot(self.weights, inputs) + self.bias return sigmoid(total)
weights = np.array([0, 1]) # w1 = 0, w2 = 1bias = 4 # b = 4n = Neuron(weights, bias)
x = np.array([2, 3]) # x1 = 2, x2 = 3print(n.feedforward(x)) # 0.9990889488055994***04 ***把神經元組裝成網絡
所謂的神經網絡就是一堆神經元。這就是一個簡單的神經網絡:
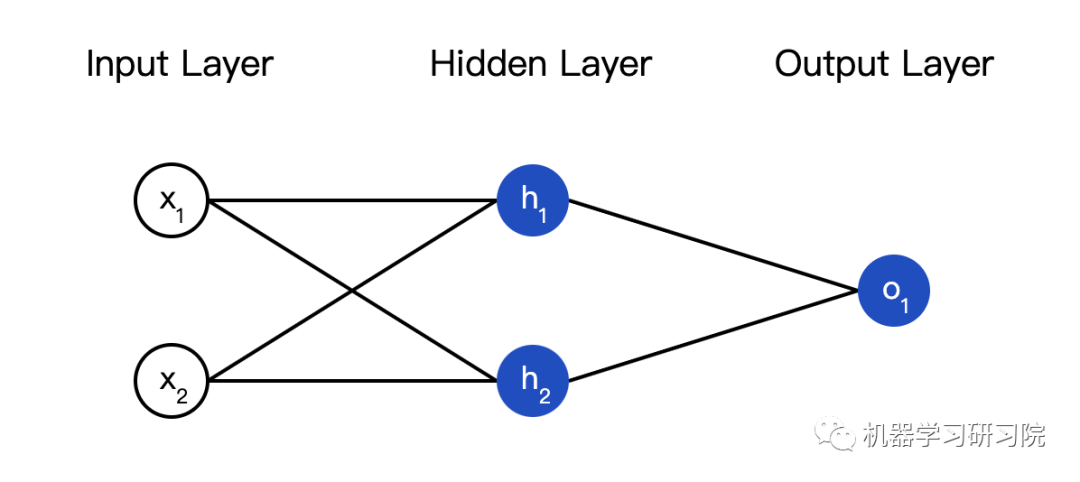
這個網絡有兩個輸入,一個有兩個神經元(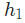 和
和 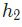 )的隱藏層,以及一個有一個神經元(
)的隱藏層,以及一個有一個神經元(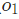 )的輸出層。要注意,
)的輸出層。要注意,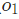 輸入就是
輸入就是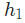 和
和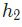 的輸出,這樣就組成了一個網絡。
的輸出,這樣就組成了一個網絡。
隱藏層就是輸入層和輸出層之間的層,隱藏層可以是多層的。
-
神經網絡
+關注
關注
42文章
4779瀏覽量
101044 -
神經元
+關注
關注
1文章
363瀏覽量
18492 -
python
+關注
關注
56文章
4807瀏覽量
84950
發布評論請先 登錄
相關推薦
labview BP神經網絡的實現
卷積神經網絡如何使用
【案例分享】ART神經網絡與SOM神經網絡
人工神經網絡實現方法有哪些?
如何構建神經網絡?
基于BP神經網絡的PID控制
卷積神經網絡一維卷積的處理過程
用Python從頭實現一個神經網絡來理解神經網絡的原理2
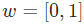
用Python從頭實現一個神經網絡來理解神經網絡的原理3

用Python從頭實現一個神經網絡來理解神經網絡的原理4





 用Python從頭實現一個神經網絡來理解神經網絡的原理1
用Python從頭實現一個神經網絡來理解神經網絡的原理1










評論