提起傅里葉變換,你會(huì)有何種表情,是恐懼,痛苦,還是。。。其實(shí),傅里葉變換真真正正的不復(fù)雜,不需要你苦讀一百遍高數(shù),只要能真正理解其中的含義,掌握它就是分分鐘的事。
1 什么是頻域
從我們出生,我們看到的世界都以時(shí)間貫穿,股票的走勢(shì)、人的身高、汽車的軌跡都會(huì)隨著時(shí)間發(fā)生改變。這種以時(shí)間作為參照來觀察動(dòng)態(tài)世界的方法我們稱其為 時(shí)域分析。而我們也想當(dāng)然的認(rèn)為,世間萬(wàn)物都在隨著時(shí)間不停的改變,并且永遠(yuǎn)不會(huì)靜止下來。但如果我告訴你,用另一種方法來觀察世界的話,你會(huì)發(fā)現(xiàn)世界是 永恒不變的,你會(huì)不會(huì)覺得我瘋了?我沒有瘋,這個(gè)靜止的世界就叫做頻域。
先舉一個(gè)公式上并非很恰當(dāng),但意義上再貼切不過的例子:
在你的理解中,一段音樂是什么呢?
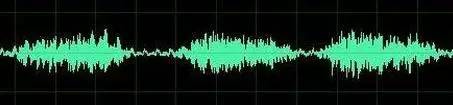
這是我們對(duì)音樂最普遍的理解,一個(gè)隨著時(shí)間變化的震動(dòng)。但我相信對(duì)于樂器小能手們來說,音樂更直觀的理解是這樣的:

好的!下課,同學(xué)們?cè)僖姟?/p>
是的,其實(shí)這一段寫到這里已經(jīng)可以結(jié)束了。上圖是音樂在時(shí)域的樣子,而下圖則是音樂在頻域的樣子。所以頻域這一概念對(duì)大家都從不陌生,只是從來沒意識(shí)到而已。
現(xiàn)在我們可以回過頭來重新看看一開始那句癡人說夢(mèng)般的話:世界是永恒的。
將以上兩圖簡(jiǎn)化:
時(shí)域:
頻域:

在時(shí)域,我們觀察到鋼琴的琴弦一會(huì)上一會(huì)下的擺動(dòng),就如同一支股票的走勢(shì);而在頻域,只有那一個(gè)永恒的音符。
所以
你眼中看似落葉紛飛變化無(wú)常的世界,實(shí)際只是躺在上帝懷中一份早已譜好的樂章。
抱歉,這不是一句雞湯文,而是黑板上確鑿的公式:傅里葉同學(xué)告訴我們,任何周期函數(shù),都可以看作是不同振幅,不同相位正弦波的疊加。在第一個(gè)例子里我們可以理解為,利用對(duì)不同琴鍵不同力度,不同時(shí)間點(diǎn)的敲擊,可以組合出任何一首樂曲。
而貫穿時(shí)域與頻域的方法之一,就是傳中說的傅里葉分析。傅里葉分析可分為傅里葉級(jí)數(shù)(Fourier Serie)和傅里葉變換(Fourier Transformation),我們從簡(jiǎn)單的開始談起。 2 傅里葉級(jí)數(shù)(Fourier Series)的頻譜 還是舉個(gè)栗子并且有圖有真相才好理解。
如果我說我能用前面說的正弦曲線波疊加出一個(gè)帶 90 度角的矩形波來,你會(huì)相信嗎?你不會(huì),就像當(dāng)年的我一樣。但是看看下圖:
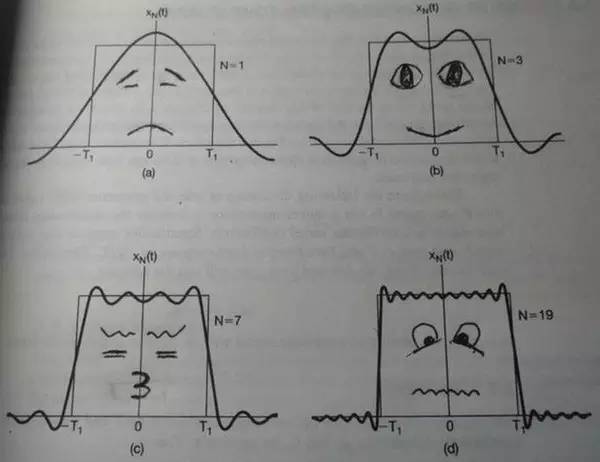
第一幅圖是一個(gè)郁悶的正弦波 cos(x)
第二幅圖是 2 個(gè)賣萌的正弦波的疊加 cos (x) +a.cos (3x)
第三幅圖是 4 個(gè)發(fā)春的正弦波的疊加
第四幅圖是 10 個(gè)便秘的正弦波的疊加
隨著正弦波數(shù)量逐漸的增長(zhǎng),他們最終會(huì)疊加成一個(gè)標(biāo)準(zhǔn)的矩形,大家從中體會(huì)到了什么道理?
(只要努力,彎的都能掰直!)
隨著疊加的遞增,所有正弦波中上升的部分逐漸讓原本緩慢增加的曲線不斷變陡,而所有正弦波中下降的部分又抵消了上升到最高處時(shí)繼續(xù)上升的部分使其變?yōu)樗?平線。一個(gè)矩形就這么疊加而成了。但是要多少個(gè)正弦波疊加起來才能形成一個(gè)標(biāo)準(zhǔn) 90 度角的矩形波呢?不幸的告訴大家,答案是無(wú)窮多個(gè)。
(上帝:我能讓你們猜著我?)
不僅僅是矩形,你能想到的任何波形都是可以如此方法用正弦波疊加起來的。這是沒有接觸過傅里葉分析的人在直覺上的第一個(gè)難點(diǎn),但是一旦接受了這樣的設(shè)定,游戲就開始有意思起來了。
還是上圖的正弦波累加成矩形波,我們換一個(gè)角度來看看:
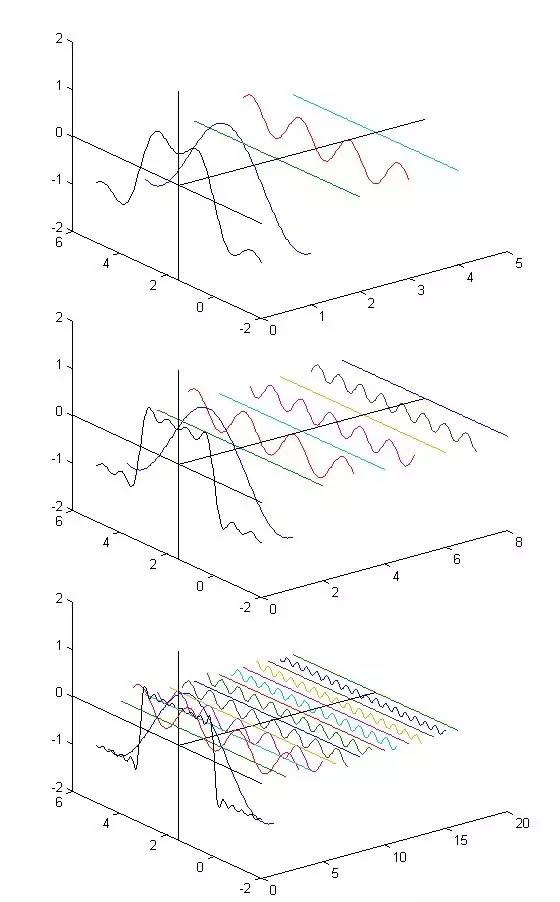
在這幾幅圖中,最前面黑色的線就是所有正弦波疊加而成的總和,也就是越來越接近矩形波的那個(gè)圖形。而后面依不同顏色排列而成的正弦波就是組合為矩形波的 各個(gè)分量。這些正弦波按照頻率從低到高從前向后排列開來,而每一個(gè)波的振幅都是不同的。一定有細(xì)心的讀者發(fā)現(xiàn)了,每?jī)蓚€(gè)正弦波之間都還有一條直線,那并不 是分割線,而是振幅為 0 的正弦波!也就是說,為了組成特殊的曲線,有些正弦波成分是不需要的。
這里,不同頻率的正弦波我們成為頻率分量。
好了,關(guān)鍵的地方來了!!
如果我們把第一個(gè)頻率最低的頻率分量看作“1”,我們就有了構(gòu)建頻域的最基本單元。
對(duì)于我們最常見的有理數(shù)軸,數(shù)字“1”就是有理數(shù)軸的基本單元。
時(shí)域的基本單元就是“1 秒”,如果我們將一個(gè)角頻率為的正弦波 cos(t)看作基礎(chǔ),那么頻域的基本單元就是
有了“1”,還要有“0”才能構(gòu)成世界,那么頻域的“0”是什么呢?cos(0t)就是一個(gè)周期無(wú)限長(zhǎng)的正弦波,也就是一條直線!所以在頻域,0 頻率也被稱為直流分量,在傅里葉級(jí)數(shù)的疊加中,它僅僅影響全部波形相對(duì)于數(shù)軸整體向上或是向下而不改變波的形狀。
接下來,讓我們回到初中,回憶一下已經(jīng)死去的八戒,啊不,已經(jīng)死去的老師是怎么定義正弦波的吧。
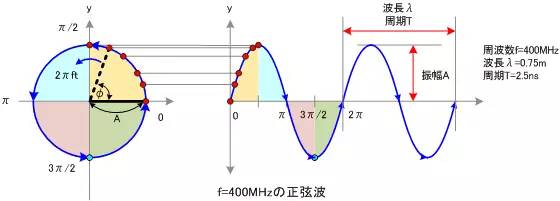
正弦波就是一個(gè)圓周運(yùn)動(dòng)在一條直線上的投影。所以頻域的基本單元也可以理解為一個(gè)始終在旋轉(zhuǎn)的圓
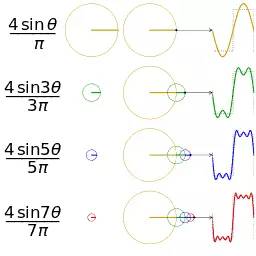
想看動(dòng)圖的同學(xué)請(qǐng)戳這里:
File:Fourier series square wave circles animation.gif
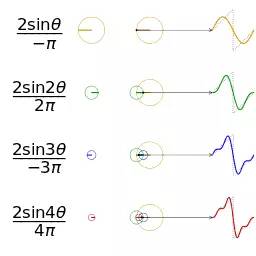
以及這里:
File:Fourier series sawtooth wave circles animation.gif
點(diǎn)出去的朋友不要被 wiki 拐跑了,wiki 寫的哪有這里的文章這么沒節(jié)操是不是。
介紹完了頻域的基本組成單元,我們就可以看一看一個(gè)矩形波,在頻域里的另一個(gè)模樣了:
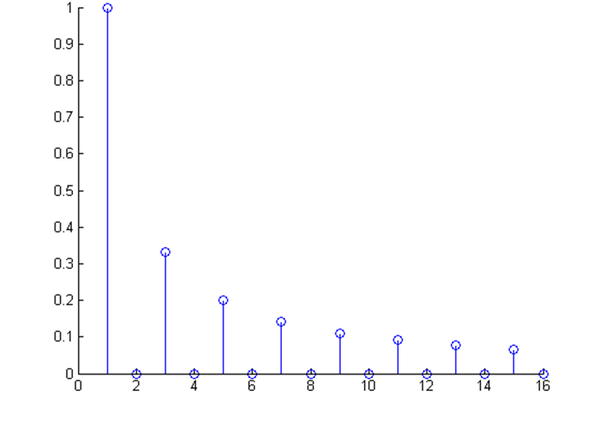
這是什么奇怪的東西?
這就是矩形波在頻域的樣子,是不是完全認(rèn)不出來了?教科書一般就給到這里然后留給了讀者無(wú)窮的遐想,以及無(wú)窮的吐槽,其實(shí)教科書只要補(bǔ)一張圖就足夠了:頻域圖像,也就是俗稱的頻譜,就是——
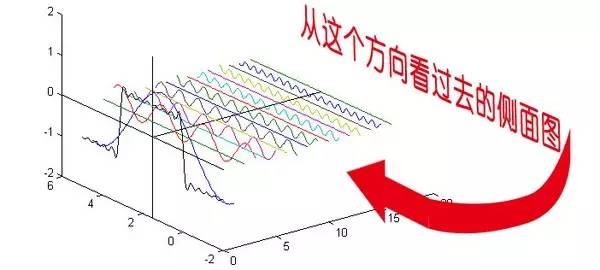
再清楚一點(diǎn):
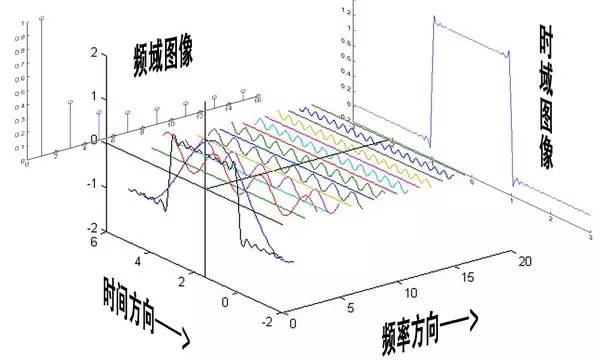
可以發(fā)現(xiàn),在頻譜中,偶數(shù)項(xiàng)的振幅都是0,也就對(duì)應(yīng)了圖中的彩色直線。振幅為 0 的正弦波。
動(dòng)圖請(qǐng)戳:
File:Fourier series and transform.gif
老實(shí)說,在我學(xué)傅里葉變換時(shí),維基的這個(gè)圖還沒有出現(xiàn),那時(shí)我就想到了這種表達(dá)方法,而且,后面還會(huì)加入維基沒有表示出來的另一個(gè)譜——相位譜。
但是在講相位譜之前,我們先回顧一下剛剛的這個(gè)例子究竟意味著什么。記得前面說過的那句“世界是靜止的”嗎?估計(jì)好多人對(duì)這句話都已經(jīng)吐槽半天了。想象 一下,世界上每一個(gè)看似混亂的表象,實(shí)際都是一條時(shí)間軸上不規(guī)則的曲線,但實(shí)際這些曲線都是由這些無(wú)窮無(wú)盡的正弦波組成。我們看似不規(guī)律的事情反而是規(guī)律 的正弦波在時(shí)域上的投影,而正弦波又是一個(gè)旋轉(zhuǎn)的圓在直線上的投影。那么你的腦海中會(huì)產(chǎn)生一個(gè)什么畫面呢?
我們眼中的世界就像皮影戲的大幕布,幕布的后面有無(wú)數(shù)的齒輪,大齒輪帶動(dòng)小齒輪,小齒輪再帶動(dòng)更小的。在最外面的小齒輪上有一個(gè)小人——那就是我們自 己。我們只看到這個(gè)小人毫無(wú)規(guī)律的在幕布前表演,卻無(wú)法預(yù)測(cè)他下一步會(huì)去哪。而幕布后面的齒輪卻永遠(yuǎn)一直那樣不停的旋轉(zhuǎn),永不停歇。這樣說來有些宿命論的 感覺。說實(shí)話,這種對(duì)人生的描繪是我一個(gè)朋友在我們都是高中生的時(shí)候感嘆的,當(dāng)時(shí)想想似懂非懂,直到有一天我學(xué)到了傅里葉級(jí)數(shù)……
3 傅里葉級(jí)數(shù)(Fourier Series)的相位譜
上一章的關(guān)鍵詞是:從側(cè)面看。這一章的關(guān)鍵詞是:從下面看。
在這一章最開始,我想先回答很多人的一個(gè)問題:傅里葉分析究竟是干什么用的?這段相對(duì)比較枯燥,已經(jīng)知道了的同學(xué)可以直接跳到下一個(gè)分割線。
先說一個(gè)最直接的用途。無(wú)論聽廣播還是看電視,我們一定對(duì)一個(gè)詞不陌生——頻道。頻道頻道,就是頻率的通道,不同的頻道就是將不同的頻率作為一個(gè)通道來進(jìn)行信息傳輸。下面大家嘗試一件事:
先在紙上畫一個(gè) sin(x),不一定標(biāo)準(zhǔn),意思差不多就行。不是很難吧。
好,接下去畫一個(gè) sin(3x)+sin(5x)的圖形。
別說標(biāo)準(zhǔn)不標(biāo)準(zhǔn)了,曲線什么時(shí)候上升什么時(shí)候下降你都不一定畫的對(duì)吧?
好,畫不出來不要緊,我把 sin(3x)+sin(5x)的曲線給你,但是前提是你不知道這個(gè)曲線的方程式,現(xiàn)在需要你把 sin(5x)給我從圖里拿出去,看看剩下的是什么。這基本是不可能做到的。
但是在頻域呢?則簡(jiǎn)單的很,無(wú)非就是幾條豎線而已。
所以很多在時(shí)域看似不可能做到的數(shù)學(xué)操作,在頻域相反很容易。這就是需要傅里葉變換的地方。尤其是從某條曲線中去除一些特定的頻率成分,這在工程上稱為濾波,是信號(hào)處理最重要的概念之一,只有在頻域才能輕松的做到。
再說一個(gè)更重要,但是稍微復(fù)雜一點(diǎn)的用途——求解微分方程。(這段有點(diǎn)難度,看不懂的可以直接跳過這段)微分方程的重要性不用我過多介紹了。各行各業(yè)都 用的到。但是求解微分方程卻是一件相當(dāng)麻煩的事情。因?yàn)槌艘?jì)算加減乘除,還要計(jì)算微分積分。而傅里葉變換則可以讓微分和積分在頻域中變?yōu)槌朔ê统ǎ?大學(xué)數(shù)學(xué)瞬間變小學(xué)算術(shù)有沒有。
傅里葉分析當(dāng)然還有其他更重要的用途,我們隨著講隨著提。 下面我們繼續(xù)說相位譜:
通過時(shí)域到頻域的變換,我們得到了一個(gè)從側(cè)面看的頻譜,但是這個(gè)頻譜并沒有包含時(shí)域中全部的信息。因?yàn)轭l譜只代表每一個(gè)對(duì)應(yīng)的正弦波的振幅是多少,而沒 有提到相位。基礎(chǔ)的正弦波A.sin (wt+θ)中,振幅,頻率,相位缺一不可,不同相位決定了波的位置,所以對(duì)于頻域分析,僅僅有頻譜(振幅譜)是不夠的,我們還需要一個(gè)相位譜。那么這個(gè) 相位譜在哪呢?我們看下圖,這次為了避免圖片太混論,我們用 7 個(gè)波疊加的圖。
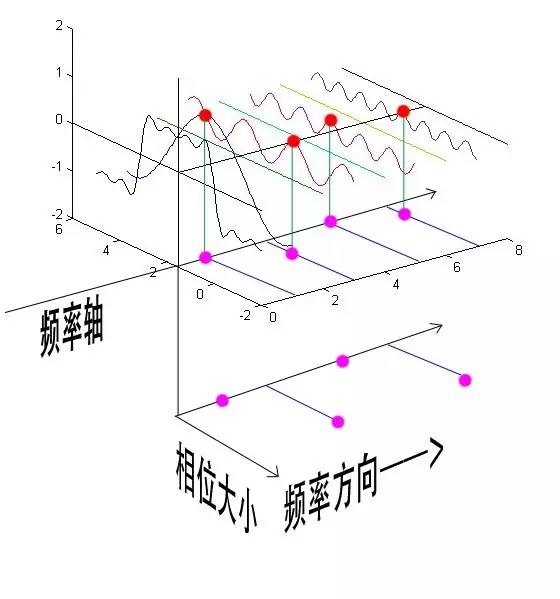
鑒于正弦波是周期的,我們需要設(shè)定一個(gè)用來標(biāo)記正弦波位置的東西。在圖中就是那些小紅點(diǎn)。小紅點(diǎn)是距離頻率軸最近的波峰,而這個(gè)波峰所處的位置離頻率軸 有多遠(yuǎn)呢?為了看的更清楚,我們將紅色的點(diǎn)投影到下平面,投影點(diǎn)我們用粉色點(diǎn)來表示。當(dāng)然,這些粉色的點(diǎn)只標(biāo)注了波峰距離頻率軸的距離,并不是相位。
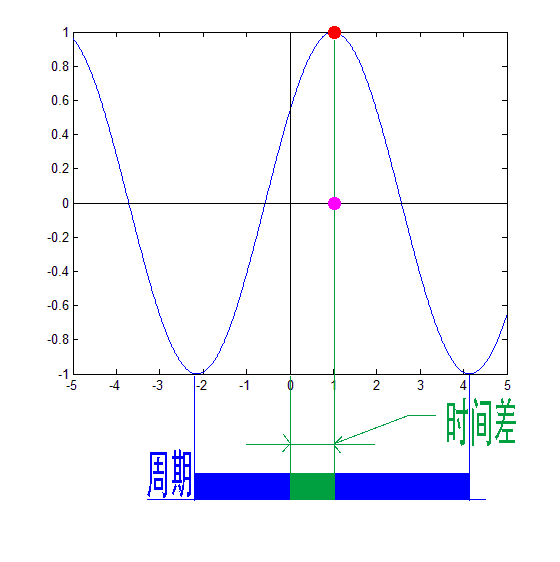
這里需要糾正一個(gè)概念:時(shí)間差并不是相位差。如果將全部周期看作 2Pi 或者 360 度的話,相位差則是時(shí)間差在一個(gè)周期中所占的比例。我們將時(shí)間差除周期再乘 2Pi,就得到了相位差。
在完整的立體圖中,我們將投影得到的時(shí)間差依次除以所在頻率的周期,就得到了最下面的相位譜。所以,頻譜是從側(cè)面看,相位譜是從下面看。下次偷看女生裙底被發(fā)現(xiàn)的話,可以告訴她:“對(duì)不起,我只是想看看你的相位譜。”
注意到,相位譜中的相位除了0,就是 Pi。因?yàn)?cos(t+Pi)=-cos(t),所以實(shí)際上相位為 Pi 的波只是上下翻轉(zhuǎn)了而已。對(duì)于周期方波的傅里葉級(jí)數(shù),這樣的相位譜已經(jīng)是很簡(jiǎn)單的了。另外值得注意的是,由于 cos(t+2Pi)=cos(t),所以相位差是周期的,pi 和 3pi,5pi,7pi 都是相同的相位。人為定義相位譜的值域?yàn)?-pi,pi],所以圖中的相位差均為 Pi。
最后來一張大集合:
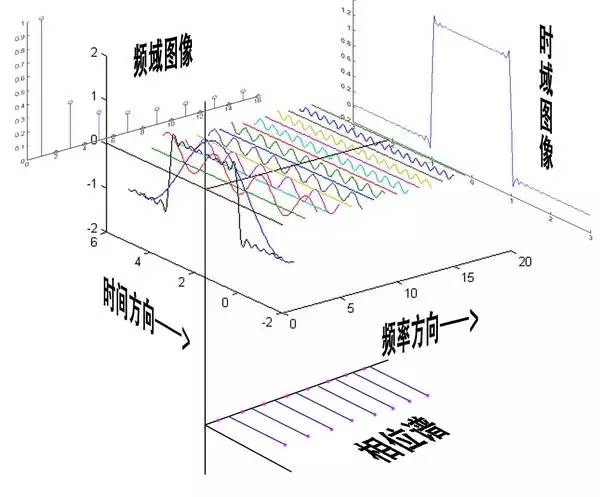
4 傅里葉變換(Fourier Tranformation) 相信通過前面三章,大家對(duì)頻域以及傅里葉級(jí)數(shù)都有了一個(gè)全新的認(rèn)識(shí)。但是文章在一開始關(guān)于鋼琴琴譜的例子我曾說過,這個(gè)栗子是一個(gè)公式錯(cuò)誤,但是概念典型的例子。所謂的公式錯(cuò)誤在哪里呢?
傅里葉級(jí)數(shù)的本質(zhì)是將一個(gè)周期的信號(hào)分解成無(wú)限多分開的(離散的)正弦波,但是宇宙似乎并不是周期的。曾經(jīng)在學(xué)數(shù)字信號(hào)處理的時(shí)候?qū)戇^一首打油詩(shī):
“ 往昔連續(xù)非周期,
回憶周期不連續(xù),
任你 ZT、DFT,
還原不回去。 (請(qǐng)無(wú)視我渣一樣的文學(xué)水平……)
在這個(gè)世界上,有的事情一期一會(huì),永不再來,并且時(shí)間始終不曾停息地將那些刻骨銘心的往昔連續(xù)的標(biāo)記在時(shí)間點(diǎn)上。但是這些事情往往又成為了我們格外寶貴 的回憶,在我們大腦里隔一段時(shí)間就會(huì)周期性的蹦出來一下,可惜這些回憶都是零散的片段,往往只有最幸福的回憶,而平淡的回憶則逐漸被我們忘卻。因?yàn)椋?是一個(gè)連續(xù)的非周期信號(hào),而回憶是一個(gè)周期離散信號(hào)。
是否有一種數(shù)學(xué)工具將連續(xù)非周期信號(hào)變換為周期離散信號(hào)呢?抱歉,真沒有。
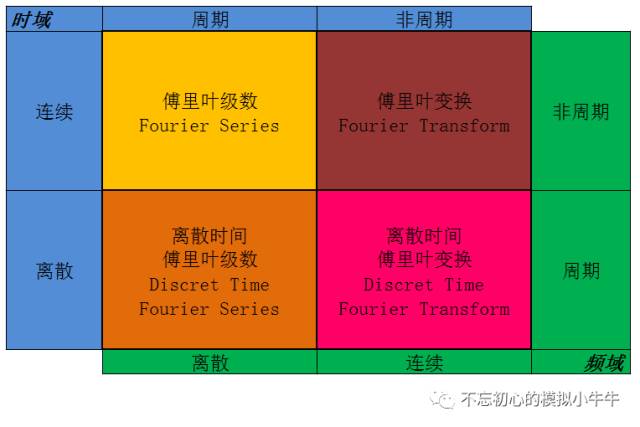
比如傅里葉級(jí)數(shù),在時(shí)域是一個(gè)周期且連續(xù)的函數(shù),而在頻域是一個(gè)非周期離散的函數(shù)。這句話比較繞嘴,實(shí)在看著費(fèi)事可以干脆回憶第一章的圖片。
而在我們接下去要講的傅里葉變換,則是將一個(gè)時(shí)域非周期的連續(xù)信號(hào),轉(zhuǎn)換為一個(gè)在頻域非周期的連續(xù)信號(hào)。
算了,還是上一張圖方便大家理解吧:
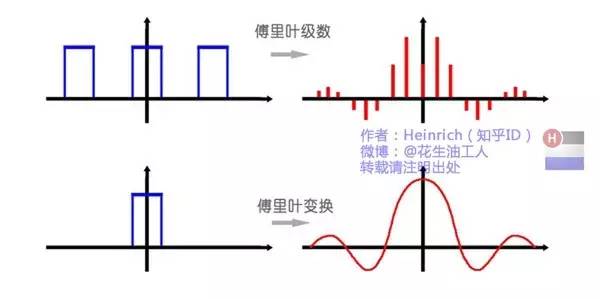
或者我們也可以換一個(gè)角度理解:傅里葉變換實(shí)際上是對(duì)一個(gè)周期無(wú)限大的函數(shù)進(jìn)行傅里葉變換。
所以說,鋼琴譜其實(shí)并非一個(gè)連續(xù)的頻譜,而是很多在時(shí)間上離散的頻率,但是這樣的一個(gè)貼切的比喻真的是很難找出第二個(gè)來了。
因此在傅里葉變換在頻域上就從離散譜變成了連續(xù)譜。那么連續(xù)譜是什么樣子呢?
你見過大海么?
為了方便大家對(duì)比,我們這次從另一個(gè)角度來看頻譜,還是傅里葉級(jí)數(shù)中用到最多的那幅圖,我們從頻率較高的方向看。
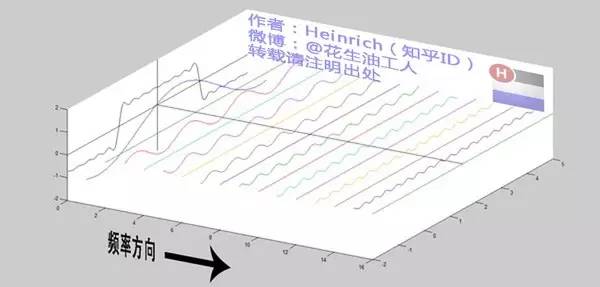
以上是離散譜,那么連續(xù)譜是什么樣子呢?
盡情的發(fā)揮你的想象,想象這些離散的正弦波離得越來越近,逐漸變得連續(xù)……
直到變得像波濤起伏的大海:
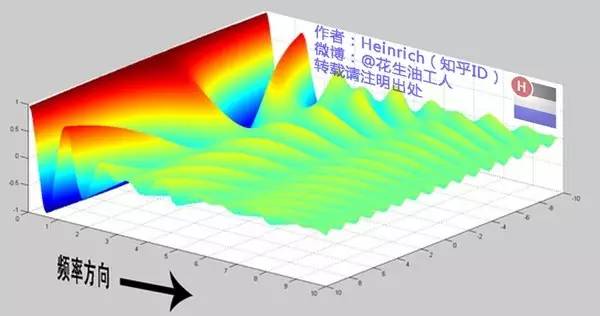
很抱歉,為了能讓這些波浪更清晰的看到,我沒有選用正確的計(jì)算參數(shù),而是選擇了一些讓圖片更美觀的參數(shù),不然這圖看起來就像屎一樣了。
不過通過這樣兩幅圖去比較,大家應(yīng)該可以理解如何從離散譜變成了連續(xù)譜的了吧?原來離散譜的疊加,變成了連續(xù)譜的累積。所以在計(jì)算上也從求和符號(hào)變成了積分符號(hào)。
不過,這個(gè)故事還沒有講完,接下去,我保證讓你看到一幅比上圖更美麗壯觀的圖片,但是這里需要介紹到一個(gè)數(shù)學(xué)工具才能然故事繼續(xù),這個(gè)工具就是——
5 宇宙耍帥第一公式:歐拉公式 虛數(shù)i這個(gè)概念大家在高中就接觸過,但那時(shí)我們只知道它是-1 的平方根,可是它真正的意義是什么呢?
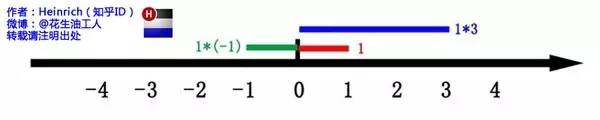
這里有一條數(shù)軸,在數(shù)軸上有一個(gè)紅色的線段,它的長(zhǎng)度是1。當(dāng)它乘以 3 的時(shí)候,它的長(zhǎng)度發(fā)生了變化,變成了藍(lán)色的線段,而當(dāng)它乘以-1 的時(shí)候,就變成了綠色的線段,或者說線段在數(shù)軸上圍繞原點(diǎn)旋轉(zhuǎn)了 180 度。 我們知道乘-1 其實(shí)就是乘了兩次 i 使線段旋轉(zhuǎn)了 180 度,那么乘一次 i 呢——答案很簡(jiǎn)單——旋轉(zhuǎn)了 90 度。
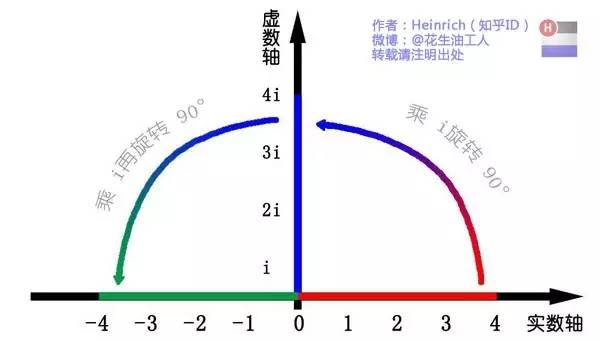
同時(shí),我們獲得了一個(gè)垂直的虛數(shù)軸。實(shí)數(shù)軸與虛數(shù)軸共同構(gòu)成了一個(gè)復(fù)數(shù)的平面,也稱復(fù)平面。這樣我們就了解到,乘虛數(shù)i的一個(gè)功能——旋轉(zhuǎn)。
現(xiàn)在,就有請(qǐng)宇宙第一耍帥公式歐拉公式隆重登場(chǎng)——
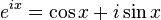
這個(gè)公式在數(shù)學(xué)領(lǐng)域的意義要遠(yuǎn)大于傅里葉分析,但是乘它為宇宙第一耍帥公式是因?yàn)樗奶厥庑问健?dāng)x等于 Pi 的時(shí)候。
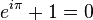
經(jīng)常有理工科的學(xué)生為了跟妹子表現(xiàn)自己的學(xué)術(shù)功底,用這個(gè)公式來給妹子解釋數(shù)學(xué)之美:”石榴姐你看,這個(gè)公式里既有自然底數(shù)e,自然數(shù) 1 和0,虛數(shù)i還有圓周率 pi,它是這么簡(jiǎn)潔,這么美麗啊!“但是姑娘們心里往往只有一句話:”臭屌絲……“
這個(gè)公式關(guān)鍵的作用,是將正弦波統(tǒng)一成了簡(jiǎn)單的指數(shù)形式。我們來看看圖像上的涵義:
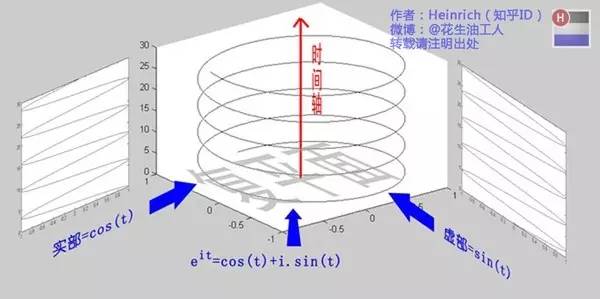
歐拉公式所描繪的,是一個(gè)隨著時(shí)間變化,在復(fù)平面上做圓周運(yùn)動(dòng)的點(diǎn),隨著時(shí)間的改變,在時(shí)間軸上就成了一條螺旋線。如果只看它的實(shí)數(shù)部分,也就是螺旋線在左側(cè)的投影,就是一個(gè)最基礎(chǔ)的余弦函數(shù)。而右側(cè)的投影則是一個(gè)正弦函數(shù)。
關(guān)于復(fù)數(shù)更深的理解,大家可以參考:
復(fù)數(shù)的物理意義是什么?
這里不需要講的太復(fù)雜,足夠讓大家理解后面的內(nèi)容就可以了。
6 指數(shù)形式的傅里葉變換 有了歐拉公式的幫助,我們便知道:正弦波的疊加,也可以理解為螺旋線的疊加在實(shí)數(shù)空間的投影。而螺旋線的疊加如果用一個(gè)形象的栗子來理解是什么呢?
光波
高中時(shí)我們就學(xué)過,自然光是由不同顏色的光疊加而成的,而最著名的實(shí)驗(yàn)就是牛頓師傅的三棱鏡實(shí)驗(yàn):
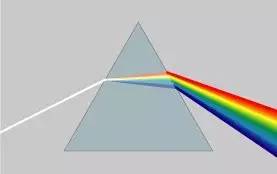
所以其實(shí)我們?cè)诤茉缇徒佑|到了光的頻譜,只是并沒有了解頻譜更重要的意義。
但不同的是,傅里葉變換出來的頻譜不僅僅是可見光這樣頻率范圍有限的疊加,而是頻率從 0 到無(wú)窮所有頻率的組合。
這里,我們可以用兩種方法來理解正弦波:
第一種前面已經(jīng)講過了,就是螺旋線在實(shí)軸的投影。
另一種需要借助歐拉公式的另一種形式去理解:
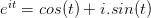
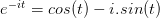
將以上兩式相加再除2,得到: 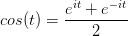
這個(gè)式子可以怎么理解呢?
我們剛才講過,e^(it)可以理解為一條逆時(shí)針旋轉(zhuǎn)的螺旋線,那么e^(-it)則可以理解為一條順時(shí)針旋轉(zhuǎn)的螺旋線。而 cos (t)則是這兩條旋轉(zhuǎn)方向不同的螺旋線疊加的一半,因?yàn)檫@兩條螺旋線的虛數(shù)部分相互抵消掉了!
舉個(gè)例子的話,就是極化方向不同的兩束光波,磁場(chǎng)抵消,電場(chǎng)加倍。
這里,逆時(shí)針旋轉(zhuǎn)的我們稱為正頻率,而順時(shí)針旋轉(zhuǎn)的我們稱為負(fù)頻率(注意不是復(fù)頻率)。
好了,剛才我們已經(jīng)看到了大海——連續(xù)的傅里葉變換頻譜,現(xiàn)在想一想,連續(xù)的螺旋線會(huì)是什么樣子:
想象一下再往下翻:
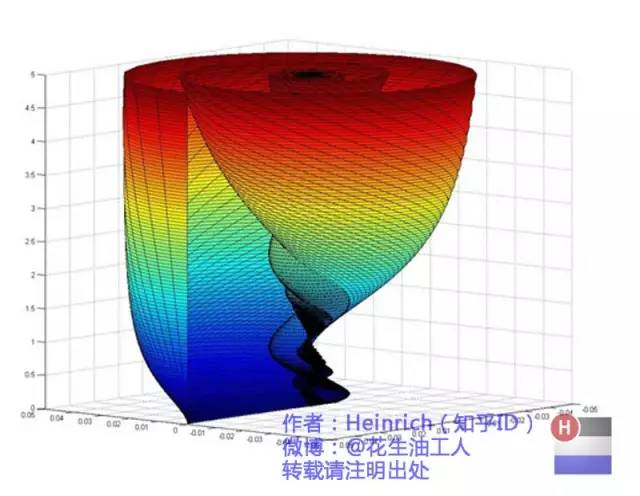
是不是很漂亮?
你猜猜,這個(gè)圖形在時(shí)域是什么樣子?
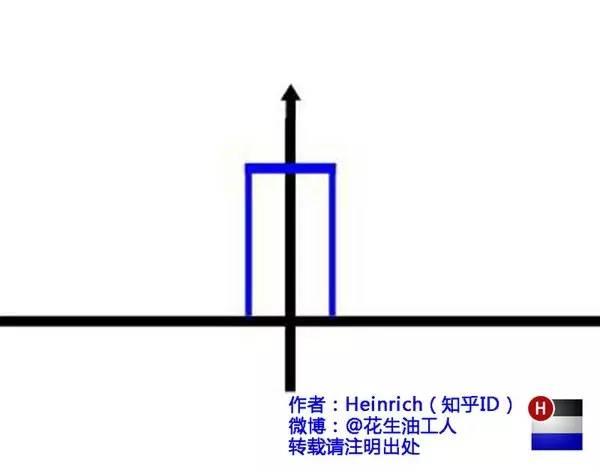
哈哈,是不是覺得被狠狠扇了一個(gè)耳光。數(shù)學(xué)就是這么一個(gè)把簡(jiǎn)單的問題搞得很復(fù)雜的東西。
順便說一句,那個(gè)像大海螺一樣的圖,為了方便觀看,我僅僅展示了其中正頻率的部分,負(fù)頻率的部分沒有顯示出來。
如果你認(rèn)真去看,海螺圖上的每一條螺旋線都是可以清楚的看到的,每一條螺旋線都有著不同的振幅(旋轉(zhuǎn)半徑),頻率(旋轉(zhuǎn)周期)以及相位。而將所有螺旋線連成平面,就是這幅海螺圖了。
好了,講到這里,相信大家對(duì)傅里葉變換以及傅里葉級(jí)數(shù)都有了一個(gè)形象的理解了,我們最后用一張圖來總結(jié)一下:
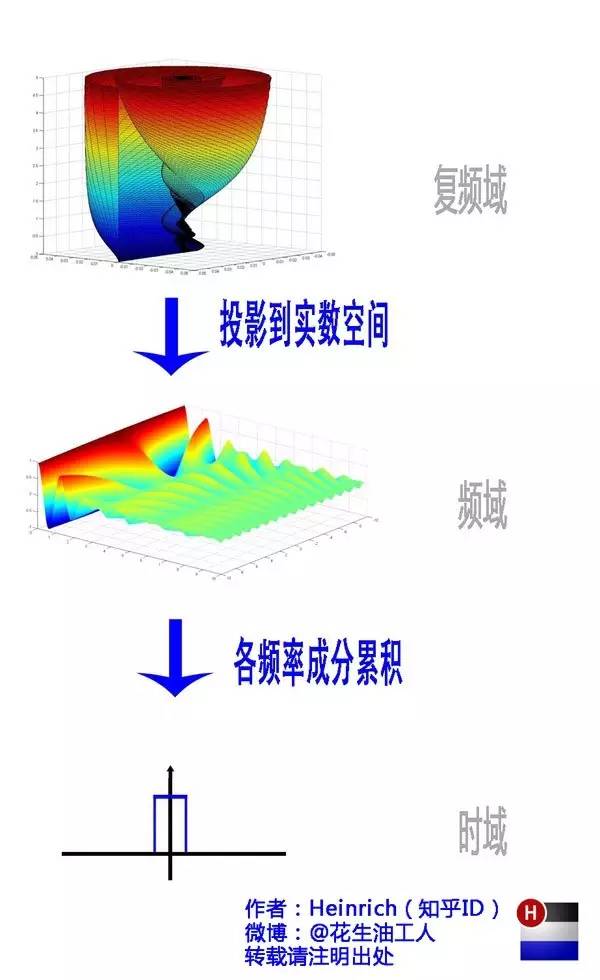
本文只是介紹了一種對(duì)傅里葉分析新穎的理解方法,對(duì)于求學(xué),還是要踏踏實(shí)實(shí)弄清楚公式和概念,學(xué)習(xí),真的沒有捷徑。但至少通過本文,我希望可以讓這條漫長(zhǎng)的路變得有意思一些。
編輯:黃飛
-
傅里葉
+關(guān)注
關(guān)注
0文章
59瀏覽量
20465 -
頻域
+關(guān)注
關(guān)注
1文章
87瀏覽量
26283 -
相位譜
+關(guān)注
關(guān)注
0文章
3瀏覽量
3288
原文標(biāo)題:把傅里葉變換都說成這樣了,看了的都明白了!
文章出處:【微信號(hào):zhuyandz,微信公眾號(hào):FPGA之家】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
讓你在不看任何數(shù)學(xué)公式的情況下理解傅里葉分析
一種基于傅里葉基神經(jīng)網(wǎng)絡(luò)的頻譜分析方法
小波與傅里葉分析基礎(chǔ)

小波與傅里葉分析基礎(chǔ)_中文版_
傅里葉級(jí)數(shù)和傅里葉變換的關(guān)系
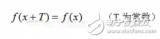
聊聊連續(xù)時(shí)間的傅里葉分析




 一種傅里葉分析新穎的理解方法
一種傅里葉分析新穎的理解方法










評(píng)論