鎖相環 (PLL) 在當今的高科技世界中無處不在。幾乎所有商業和軍用產品都在其運行中使用它們,相位(或 PM)噪聲是一個主要問題。頻率(或 FM)噪聲密切相關(瞬時頻率是相位的時間導數)并且通常在相位噪聲的保護傘下考慮(也許兩者都可以被認為是“角度噪聲”)。幅度(或 AM)噪聲是另一個考慮因素。
雖然兩者都會影響 PLL 性能,但振幅噪聲通常是自限性的,不會產生任何影響。因此,PLL 輸出和 RF 組件的相位噪聲是主要問題。當然,輸出相位噪聲是最重要的問題——它主要取決于每個組件的相位噪聲。
許多因素都會導致元件相位噪聲,例如電源、EMI 和半導體異常等等。了解這些因素使我們能夠實施組件相位噪聲的緩解策略,并最終實施輸出相位噪聲。
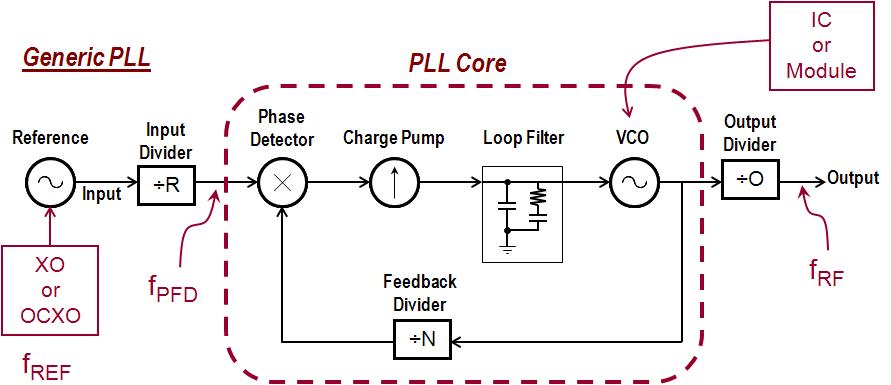
我們討論的 PLL 屬于模擬硬件類型,而不是數字或軟件類型。這種 PLL 的一般拓撲結構是一個單環路系統,其中包含精密參考、參考分頻器、反饋分頻器、可能的預分頻器、電壓或電流(也稱為電荷泵)鑒相器、環路濾波器和壓控振蕩器 (VCO) .這些組件可能都是分立的,或者其中一些可能包含在 IC 中。無論如何,我們展示了如何分析一般的相位噪聲,以及 RF 分量相位噪聲如何通過 PLL 傳播以確定其輸出相位噪聲。
在第 1 部分中,我們討論了相位噪聲的一些簡要理論和典型測量及其分析(建模、仿真和傳播),并詳細展示了大多數計算機輔助設計 (CAD) 應用程序使用的方法。
相位噪聲的簡要理論和典型測量
相位噪聲是一個重要而復雜的課題,研究正在進行中,對其起源的理解也很脆弱,數學基礎也有問題。然而,許多近似值和變通方法被用來產生極好的理論和實踐結果。1,2,3這是一個成熟的學科,有很多可用的文獻。有幾種儀器可以精確測量相位噪聲,并且無數帶有 PLL 的現場系統都具有受控的相位噪聲特性。
在這里,我們簡要回顧時域和頻域中的相位噪聲理論,以及基帶 (BB) 領域(對 RF 載波信號進行相位調制的 BB 噪聲信號)和 RF 領域(RF由 BB 噪聲信號進行相位調制的載波信號)。
此外,我們還總結了頻域中兩個領域的典型相位噪聲測量,當然,它們是同一現象的不同等效表示,并給出相同的結果。
BB 領域被認為是不太重要的領域,但對于相位噪聲的起源很重要,并且提供比 RF 領域更好的測量精度。RF 領域被認為是更重要的領域,并且對相位噪聲的可觀察表現很感興趣,盡管它的測量精度不如 BB 領域。1,8此外,我們調查了兩種測量類型的等效性。
正如所有物理學中眾所周知的那樣,存在確定性和非確定性(也稱為隨機、隨機或概率)過程。在 PLL 中,這些過程是信號,可以在時域和頻域兩個域中表示,兩個域通過傅立葉變換通過變換理論相關聯。
要使用(在本例中為連續)變換理論,系統被建模為(連續)線性時不變網絡,這意味著 PLL 必須處于鎖定狀態。相反,處于解鎖狀態的 PLL 模型是非線性的;因此,不能應用變換理論。
此外,域之間的轉換對于確定性信號是直接的,對于隨機信號是間接的。直接意味著直接在時域和頻域之間進行變換,因為存在直接變換。間接是指域之間的轉換有一個中間步驟,就是計算隨機信號的自相關函數,取其時間平均,然后進行變換,因為直接變換是不存在的。6個
然后,在 RF 系統或 RF 組件中,當已知和未知來源的內部和/或外部 BB 隨機(噪聲)信號對系統或組件的內部 RF 確定性(載波)進行相位調制時,會產生相位噪聲) 信號。當然,相位噪聲是一種隨機現象或信號,因此充滿了間接變換。
通常,對于頻域中的隨機信號,作為電壓譜密度 (VSD) 的頻譜是不存在的。然而,頻譜確實以功率譜密度 (PSD) 的形式存在,只有幅度信息而沒有相位信息。相比之下,對于頻域中的確定性信號,頻譜通常確實以 VSD 形式存在,具有幅度和相位信息,當然,擴展后也具有 PSD。
此外,在 BB 領域的頻域中,頻譜是低通(或準低通)函數,而對于 RF 領域,頻譜是帶通函數。此外,在本次討論中,我們僅使用正單邊 (OS) 頻譜和正單邊帶 (SSB) 相位噪聲信息,而不是雙邊 (TS) 頻譜和雙邊帶 (DSB) 相位-噪音信息。
我們還注意到,在時域中,相位噪聲通常稱為相位抖動,而在頻域中,它通常稱為規定相位噪聲。這兩個域中的現象通過瞬時頻率定義為相位的時間導數而相關聯。1,8,10
考慮到上述背景,我們簡要回顧了時域和頻域的一些理論以及BB 領域的域之間的轉換。在這個領域,我們的理論和分析原則上基本上存在,因為我們的隨機(噪聲)信號在時域(這是我們的分析開始的地方)沒有解析表達式。因此,經過變換后,頻域上沒有解析表達式。我們有以下數學表示和變換步驟:6,7,8
1.時域函數或相位波形,它是一個真實的(非復雜的)隨機過程,具有零均值高斯概率密度函數,?(t):
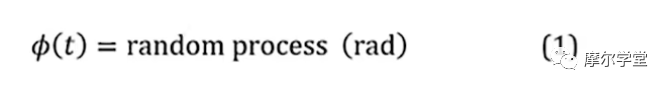
其中t是時間。
2. (1)的自相關函數,R?(t,τ):
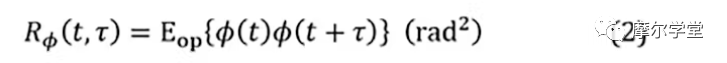
其中τ是測量之間的正時間增量,Eop{...}是統計平均運算符。
3. 等式 2 的時間平均值的傅立葉變換,給出非歸一化 (UN) BB頻域函數或 PSD,W?(ξ)或WdB?(ξ):
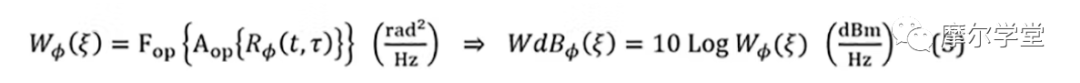
其中ξ是頻率,Aop{...}是時間平均算子,Fop{...}是傅里葉變換算子。典型的相位波形圖及其 UN BB PSD如圖 1a 和 1b所示。
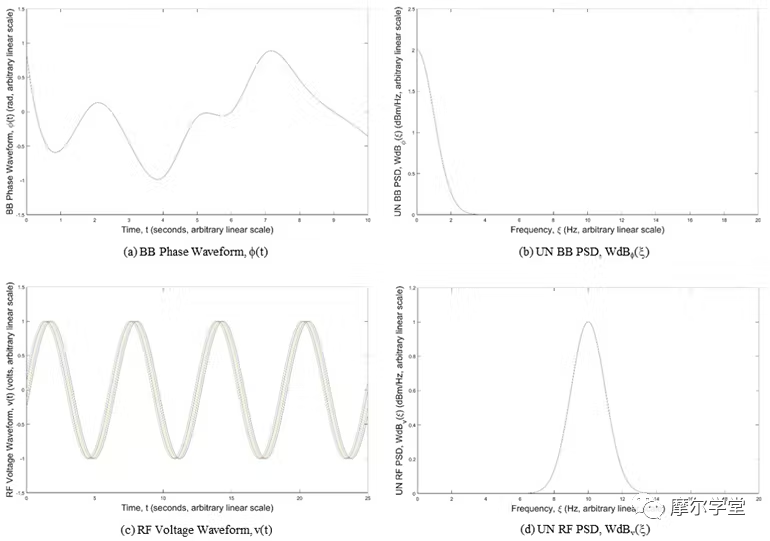
1. (a) 基帶 (BB) 相位波形 ?(t),(b) 非歸一化 (UN) BB 功率譜密度 (PSD),Wdb ? (ξ),(c) 的相位噪聲理論中的典型圖) RF 電壓波形 v(t),以及 (d) UN RF PSD,Wdbv(ξ)。
接下來,我們簡要回顧時域和頻域中的類似理論以及射頻領域的域間轉換。在這個領域,我們的理論和分析是相當分析的,因為在時域中我們的確定性(載波)信號有一個相當分析的表達式(這又是我們分析的起點)。因此,經過變換后,在頻域上有一個相當解析的表達式。
對于≤ 0.2 弧度(≤ 11.5°)的“合理”相位波形偏差(也稱為小角度...、小調制指數...或窄帶 PM...近似值),其中 PM 頻譜與DSB AM 頻譜——這是所有實際相位噪聲問題的情況——我們有以下數學表示和變換步驟(為簡潔起見未顯示細節):7、8、10
4.時域函數或電壓波形(也是BB參數的函數),v(t):
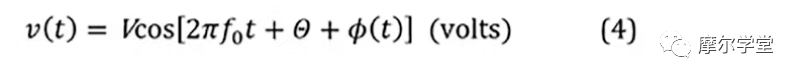
其中V是統計平均振幅,f0是載波頻率,Θ是初始相位(V是一般振幅的特例,V + a(t),其中a(t)是統計零均值a(t)= 0的振幅噪聲,因為如前所述,它是自我限制的并且沒有任何后果):
5. 等式 4 的自相關函數(同樣也是 BB 參數的高斯概率密度函數),Rv(τ):
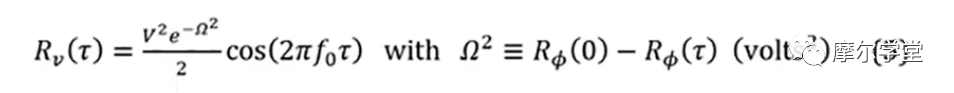
其中Rφ(0)是Rφ(τ),其中τ = 0,這是φ(t)的方差。
6. 等式 4 的時間平均值的傅立葉變換(同樣也是 BB 參數的函數)給出 UN RF頻域函數或 PSD,Wv(ξ)或WdBv(ξ):
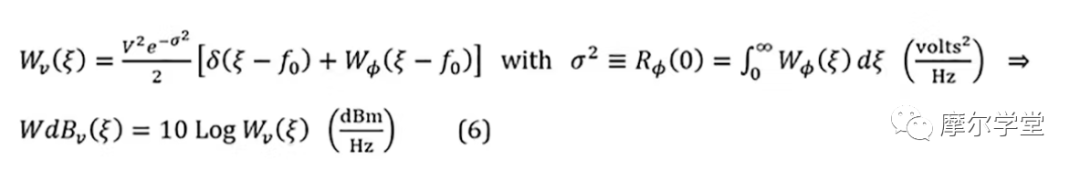
其中d(ξ–f0)是 Dirac delta 或單位脈沖函數,W?(ξ–f0)是 UN BB PSD,W?(ξ),通過調制過程從 BB 領域轉換到 RF 領域。典型的電壓波形圖及其 UN RF PSD如圖 1c 和 1d所示。
需要注意的是,如果?(t)是嚴格平穩的(一個合理的假設),則可以證明v(t)至少是廣義平穩的。在這種情況下,Weiner-Khinchin 定理成立,R?(t,τ)和Rv(t,τ)僅成為 τ 的函數,[R?(t,τ)→R?(τ)和Rv(t,τ)→Rv(τ)],因此不需要找到R?(τ)和Rv(τ)的時間平均值。因此,W?(ξ)和Wv(ξ)是R?(τ)和Rv(τ)本身的傅里葉變換。1,6,7,9
然后,根據上述簡要理論,我們總結了頻域中 BB 和 RF 領域相位噪聲的典型測量。
BB 領域的測量
在上面的 UN BB PSD 中,選擇了一個特定的頻率,并將其在 1 Hz 帶寬中的功率除以低通頻譜上的總積分功率,得到歸一化 (NM) BB PSD,L?(ξ)或LdB?(ξ):
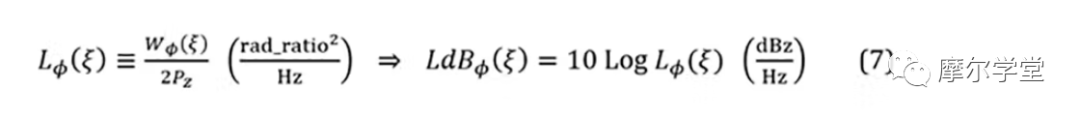
其中ξ是特定頻率,Pz是總積分低通功率,dBz 是相對于Pz的分貝數。測量是間接的,使用信號源分析儀,解調、測量、處理和顯示 BB 信號以產生L?(ξ)或LdB?(ξ)[W?(ξ)包含 DSB 信息,因此因子L?(ξ)的計算需要 2給 SSB 信息]。它被認為比在 RF 領域所做的更準確。1,8
射頻領域的測量
在上面的 UN RF PSD 中,選擇了一個特定的載波偏移頻率。它在 1 Hz 帶寬內的功率除以帶通頻譜上的總積分功率,得到 NM RF PSD、Lv(f)或LdBv(f):
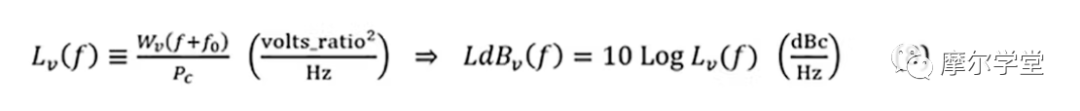
其中f是載波的特定偏移頻率 (f=ξ? f0其中ξ≥f0),Pc是總積分帶通功率,dBc 是相對于Pc的分貝數。測量是直接的,使用具有相位噪聲處理能力的頻譜分析儀測量、處理和顯示射頻信號以產生Lv(f)或LdBv(f)。它被認為不如在 BB 領域中所做的那樣準確。1,8
兩種測量的等效性
如前所述,L?(ξ)或LdB?(ξ)和Lv(f)或LdBv(f)是同一現象的不同表示,邏輯上應該對所有實際相位噪聲問題給出相同的結果(其中,也如前所述,相位偏差被認為是“合理的”)。因此,對于這種情況,它們是等價的并且給出相同的結果,稱為 NM PSD、L(f)或LdB(f)。BB 和 RF 領域下標 (?和v) 被刪除并且不使用下標(即使是“合理”條件也有一些異常,必須使用具有學術和實踐論據的近似值):1,10
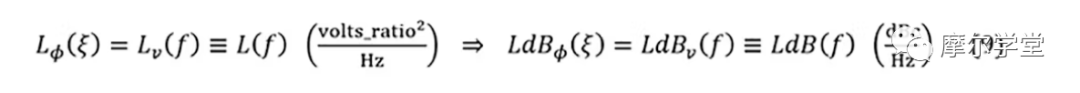
其中,典型顯示的f是 x 軸載波的偏移頻率,單位為 Hz,對數標度,LdB(f)是 y 軸的 NM RF PSD,單位為 dBc/Hz,線性標度規模,對于上述間接和直接測量,最終將一切與 RF 領域相關聯(圖 2)。
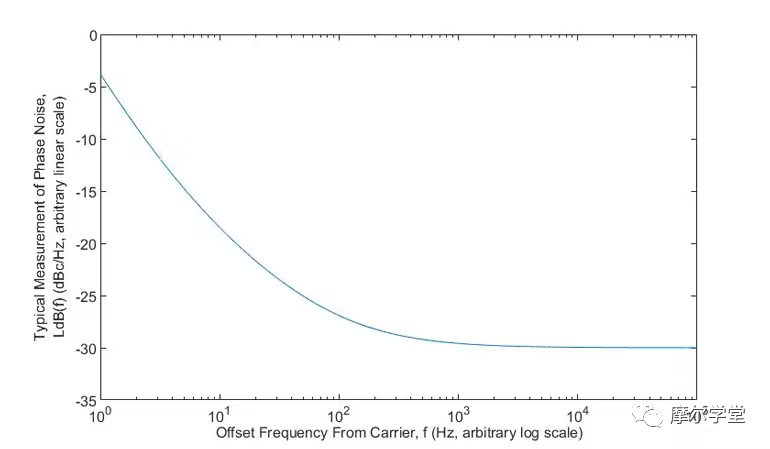
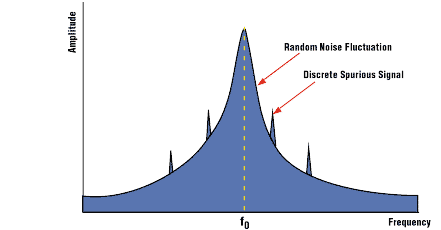
2. 頻域中基帶和射頻領域相位噪聲的典型測量。
需要注意的是,如果不滿足“合理”條件,則必須使用貝塞爾函數數學將L?(ξ)與Lv(f)聯系起來。因此,這兩種測量不會等同,會給出不同的結果,并且會被認為是災難性的問題。
相位噪聲的分析(建模、仿真和傳播)
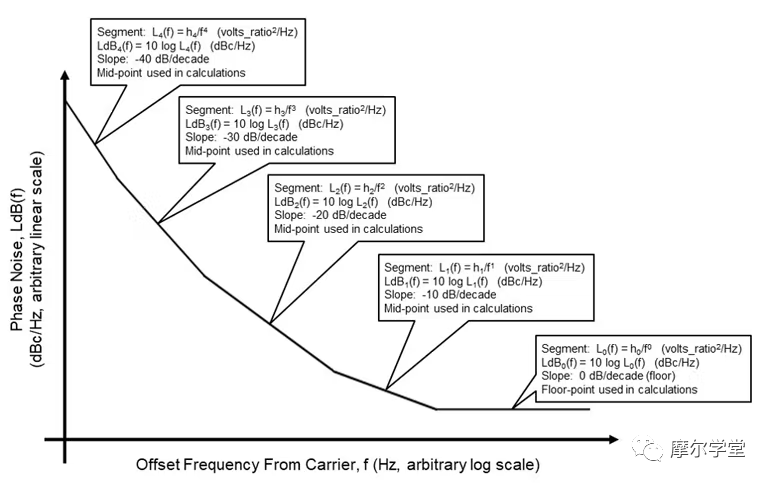
3. 用于相位噪聲分析(建模、仿真和傳播)的一般相位噪聲模型。
有了以上信息,我們現在開始分析 PLL 中的相位噪聲,以及一般如何對其進行建模和仿真。還討論了 RF 分量相位噪聲如何通過 PLL 傳播以確定其輸出相位噪聲。通常,相位噪聲可以使用“通用相位噪聲模型”(圖 3)及其標準整數冪級數進行有效建模:
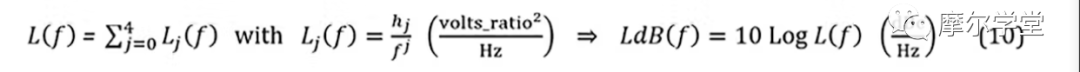
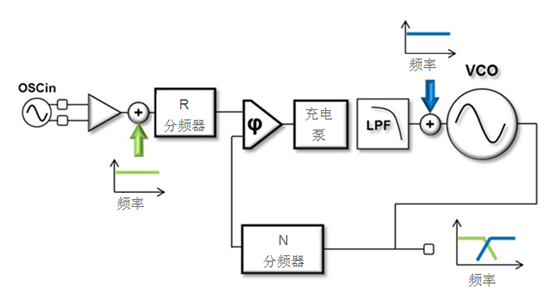
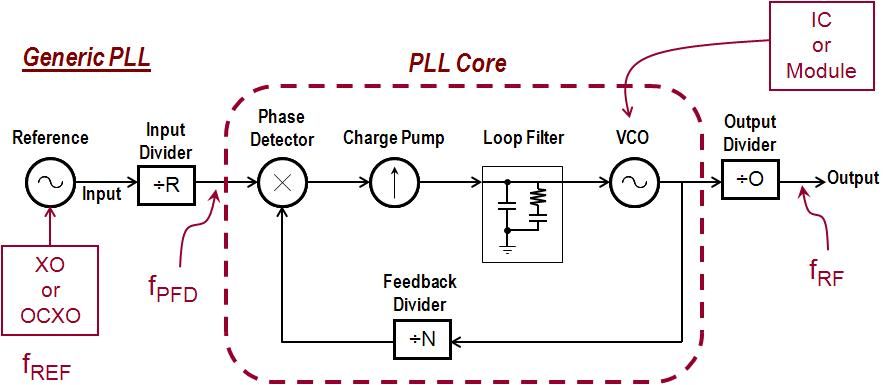
其中h是加權系數,f是載波的偏移頻率。1,7然后使用任何標準應用程序對其進行仿真(在本例中,我們使用 MATLAB)。最后,組件相位噪聲通過 PLL 的傳播以確定其輸出相位噪聲是使用通用 PLL 模塊“圖表和相位噪聲傳播模型”完成的(圖 4)。
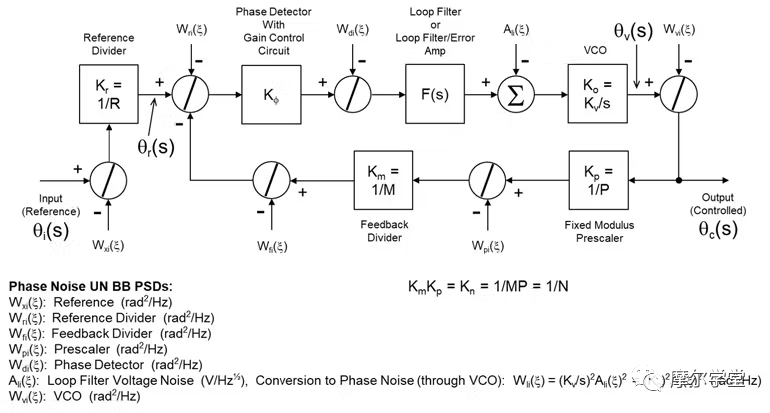
4. 用于相位噪聲分析(建模、仿真和傳播)的通用 PLL 框圖和相位噪聲傳播模型。
此外,為了簡化分析,所有組件的相位噪聲都近似為不相關(合理的假設),以便它們的 NM PSD 直接相加,而不必處理相關信號,這會使分析變得非常復雜。然后使用以下相位噪聲分析程序進行分析:4,5
1. PLL 必須表示為(在本例中為連續的)線性時不變網絡,這意味著它必須鎖定在其輸出之一。
2. 所有組件的相位噪聲必須近似為不相關。
3. 每個組件的相位噪聲圖都是從其數據表中獲得的,“通用相位噪聲模型”(圖 3)適合每個組件的圖,以確定匹配的通用模型的部分(其中一些可能不存在)每個組件的情節。
4. 對于每個組件的擬合通用相位噪聲模型,一個相位噪聲點,LdBj(fk)(j,k=0,a;1,b ;2,c;3,d;4,e),在每個獲得段用于計算(通常使用段內的中點)。將所有對數值轉換為線性值,LdBj(fk)TLj(fk):
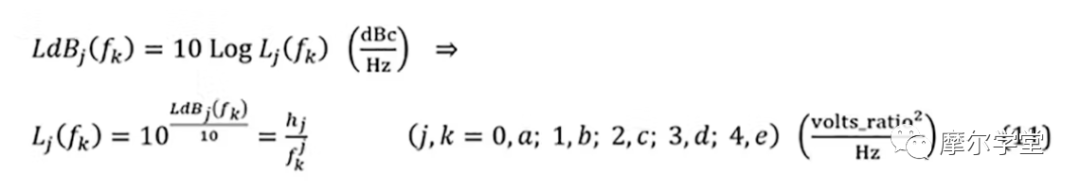
5. 每個組件的擬合通用相位噪聲模型系數hj是使用來自步驟 4 的相位噪聲點(其中一些可能為零)計算的:
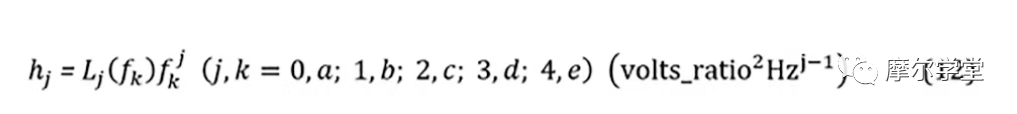
6. 來自步驟 5 的每個組件的擬合通用相位噪聲模型系數hj用于形成每個組件的相位噪聲模型Lci(f):
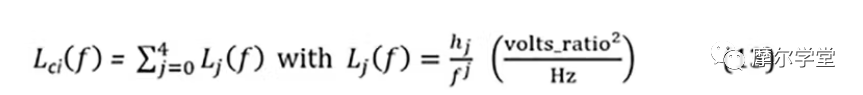
可以對其進行模擬以產生分量相位噪聲曲線。
7. 來自步驟 6 的每個組件的相位噪聲模型Lci(f)乘以其適用的傳遞函數(輸出或誤差;稍后討論)幅度平方,|T(f)|2,得到其傳播的相位噪聲模型,Lco(f):
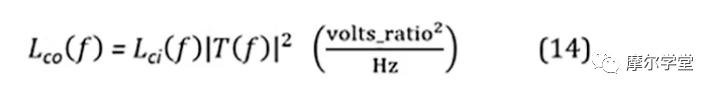
可以對其進行模擬以產生組件傳播的相位噪聲曲線。
8. 來自步驟 7 的每個組件的傳播相位噪聲模型Lco(f)與所有其他相加在一起以獲得輸出相位噪聲模型L至(f):
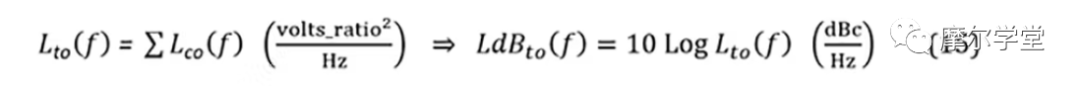
可以對其進行仿真以產生輸出相位噪聲曲線。
這就是我們的相位噪聲分析(建模、仿真和傳播)過程。如前所述,這是大多數 CAD 應用程序用于相位噪聲分析的方法。
審核編輯:劉清
-
鎖相環
+關注
關注
35文章
590瀏覽量
87847 -
濾波器
+關注
關注
161文章
7859瀏覽量
178689 -
pll
+關注
關注
6文章
781瀏覽量
135279 -
VCO
+關注
關注
13文章
190瀏覽量
69280 -
CAD
+關注
關注
17文章
1093瀏覽量
72670
原文標題:鎖相環中的相位噪聲建模、仿真和傳播(一)
文章出處:【微信號:moorexuetang,微信公眾號:摩爾學堂】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何根據基本的數據表規格估算出PLL的相位噪聲




 如何在PLL輸出端產生最低的相位噪聲?
如何在PLL輸出端產生最低的相位噪聲?











評論