作者：劉永平，魏凌強丨EDC電驅未來

行星輪系作為目前先進齒輪傳動機構中的一種，具有結構緊湊、質量輕、承載能力強、傳遞功率范圍大、效率高及壽命長等優點。但其復雜的結構和大量的計算，導致對設計人員的水平有一定的，如果設計或制造不當，會使行星齒輪的傳動精度受到一定的影響，導致傳動過程產生一定的振動和噪聲。通常情況下，有以下幾方面影響傳動系統的噪聲：

1）設計時，由于行星輪系參數選擇不當，導致齒輪副重合度過小；輪齒修形方式不當或沒有修形；齒輪箱的結構設計不合理等。

2）輪齒加工時，由于基節誤差或齒形誤差過大，導致齒側間隙過大；加工表面粗糙度偏大等。

3）輪系裝配時，由于軸的平行度差或回轉精度不高，軸或軸承的剛度不足等，導致輪系精度降低。

4）另外，輸入扭矩、負載扭矩的波動及軸系的扭振等也會使傳動系統產生一定的噪聲。

針對齒輪副傳動過程中過大的傳遞誤差和一定的載荷偏載導致的噪聲問題，常用方法就是對齒輪產生沖擊的部分進行修形，使其接觸部分面積增大，沖擊減小。恰當的修形量，有利于提高齒輪的彈性，從而進一步改善齒輪的嚙合性能，減小振動和噪聲。

對齒輪修形時一般會根據經驗修形，即先加工出齒面，再進行接觸斑點實驗，得到不同工況下的齒面接觸斑點，然后根據得到的接觸斑點對輪齒進行修形。這種方法顯然要進行多次的修形實驗來確定最優的修形方式，導致成本大且時間長。而本文利用KISSsoft軟件可以很好地模擬這些實驗過程，通過不同的修形方式及組合，來得到最佳的齒輪副嚙合的傳動誤差、齒面載荷分布以及接觸斑點，以實現行星減速機的降噪目的。相比傳統方法，利用該軟件可以有效地節省加工成本并縮短設計周期。

1 齒輪修形原理

一般來說，齒輪修形分為齒廓修形和齒向修形，具體如圖1和圖2所示。齒向修形主要針對降低齒面載荷分布和減輕齒面偏載以提高齒輪承載能力，而齒廓修形主要是降低齒輪副嚙合沖擊從而減少噪聲。

理論意義上，具有精確的漸開線的剛性齒輪能夠實現嚙合過程中主、從動輪的基節處處相等。但實際中，在一定齒輪副嚙合力作用，作為彈性體的齒輪副會產生相應的彈性變形，使處于嚙合線位置的主、從動輪的基節出現變化，不再相等。

如圖3所示，當齒對2進入嚙入位置時，由于齒對1的彈性變形，使主動輪基節Pb1小于從動輪基節Pb2，齒輪嚙入點的嚙合力瞬間變大，形成了嚙入沖擊。同樣的，當齒對1快要脫離嚙合接觸時，由于齒對2的彈性變形，使得主動輪基節Pb1大于從動輪基節Pb2，導致主動輪的齒頂沿著被動輪的齒根刮行，形成嚙出沖擊，如圖4所示。為了降低基節誤差和減小齒輪受載彈性變形所導致的嚙入沖擊和嚙出沖擊，通常從齒高方向向下切除一部分材料，改變齒廓形狀，即齒廓修形，以消除齒輪副在嚙入和嚙出位置的幾何干涉。

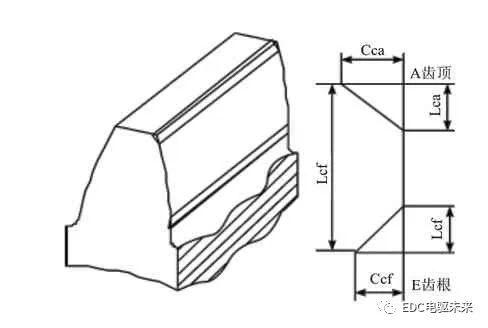
圖1 齒廓修形

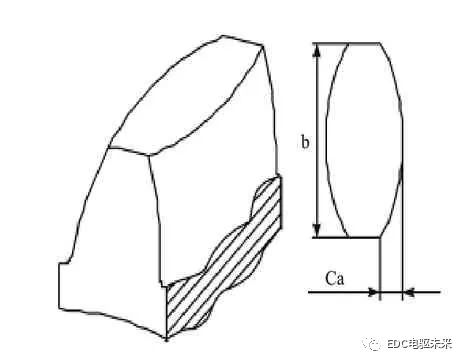
圖2 齒向修形

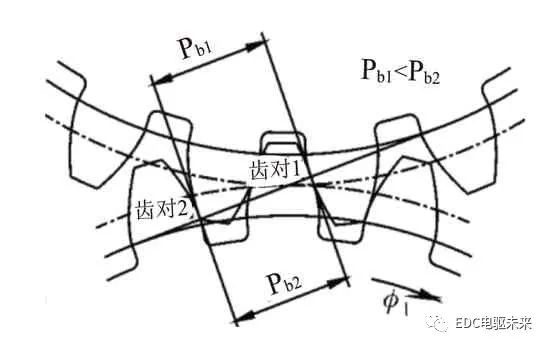
圖3 嚙入沖擊

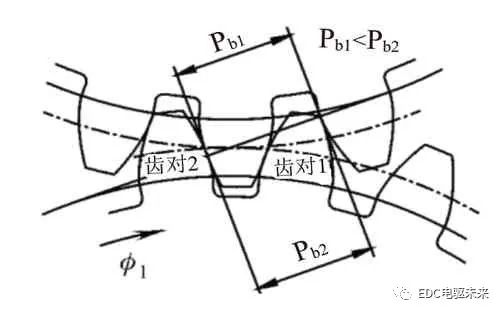
圖4 嚙出沖擊

對于齒廓修形，ISO標準的公式為：

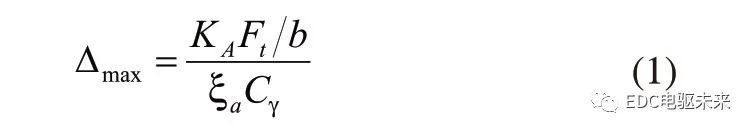
式中，?max為最大修形量，ξa為端面重合度，KA為工況系數，Ft/b為單位齒寬上的圓周力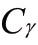，為齒輪嚙合剛度。

對于齒向修形，英國重點考慮齒輪的彈性變形因素，計算公式為：

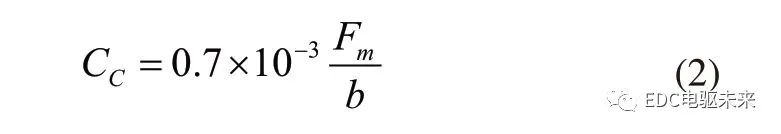
日本則側重考慮齒輪的精度，計算公式為：

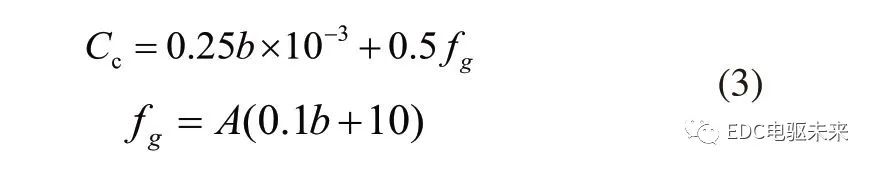
ISO主要考慮了齒輪嚙合的齒向誤差因素，計算公式為：

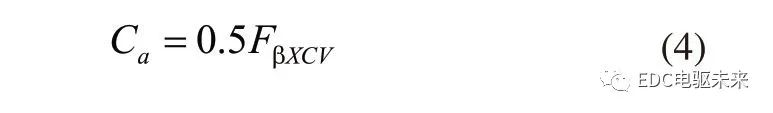
式中，Cc、Ca為修形量，Fm為作用在齒寬面上的圓周力，b為齒面寬度，fg為齒向誤差，FβXCV為嚙合齒向誤差。

但是，無論齒廓修形還是齒向修形都是在特有的經驗背景下進行修形的，因此并不適用所有的場合，而不恰當的修形，反而會進一步降低齒輪傳動性能，達不到預期的效果。

2 行星輪系修形技術研究

Kisssoft軟件對齒輪修形時，應用鼓形、線形、拋物線和螺旋角等不同修形方法或其組合，通過對齒輪進行齒廓、齒向或對角修形，從而得到合理的修形方式，達到最優修形效果。在Kisssoft軟件完成修形之后，可分析齒輪強度在修形前后的變化來判斷修形的好壞，同時也可以直觀比較齒輪傳遞誤差和接觸斑點的變化作為參考。本節利用Kisssoft軟件，通過不同的修形方式及組合的對比分析，得出一種最佳的修形方式。

2.1 行星輪系參數建模分析

以某行星齒輪減速機為例，該輪系以太陽輪作為輸入，行星架為輸出，額定輸出力矩為330Nm；額定輸入轉速為3000rpm。齒輪參數如表1所示。

表1 齒輪基本參數表

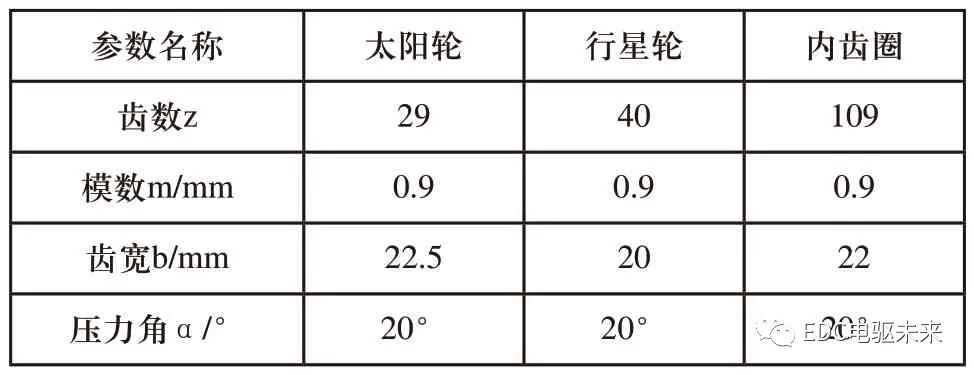
根據表1中的參數，在SolidWorks軟件中建立精確模型后導入Kisssoft軟件中，具體三維模型如圖5所示。

圖5 行星輪系三維模型圖

對其運動進行仿真，得到行星輪與太陽輪、行星輪與內齒圈的輪齒嚙合圖，如圖6和圖7所示。通過仿真分析可看出輪齒在嚙合過程中無干涉。

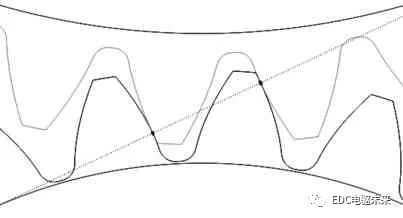
圖6 太陽輪和行星輪運動仿真圖

圖7 行星輪與內齒圈運動仿真圖

當滑動比在-1與1之間，且越接近0時，齒輪傳動的噪音越低。經分析，行星輪與太陽輪、行星輪與內齒圈的滑動比均在-1與1內，如圖8和圖9所示，從圖中可以看出行星輪與內齒圈滑動比接近0，證明其工作狀態良好。

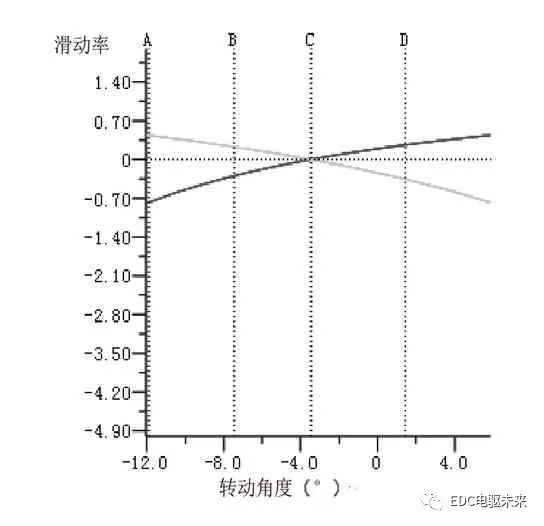
圖8 太陽輪與行星輪滑動比圖

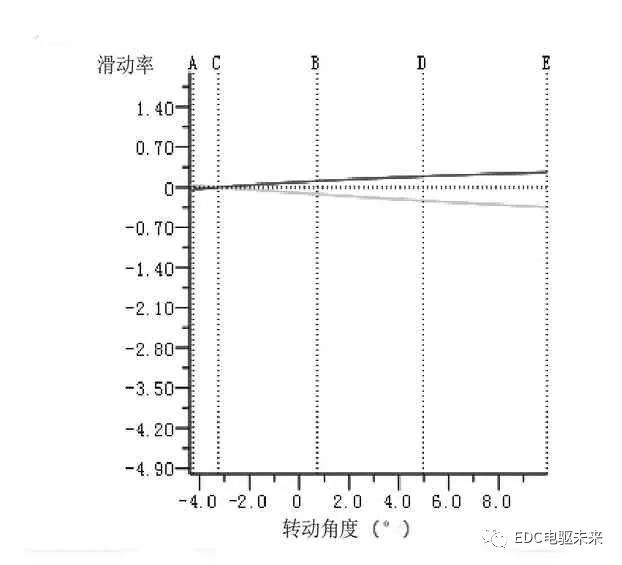
圖9 行星輪與內齒圈滑動比圖

2.2 修形分析

由于行星輪既與太陽輪嚙合又和內齒圈嚙合，所以一般只需對行星輪進行修形，其他齒輪不修形。利用Kisssoft軟件，對某行星減速器的行星輪分別在齒頂、齒根以及齒頂和齒根等位置進行短齒廓、長齒廓、短圓弧、長圓弧、短漸開線、長漸開線、短齒廓圓弧過渡和長齒廓圓弧過渡等修形方式分析（限于篇幅，僅列出最優一組修行量數據，如表2所示）。修行量計算如下：

1）計算有效齒廓嚙合點的曲率半徑：

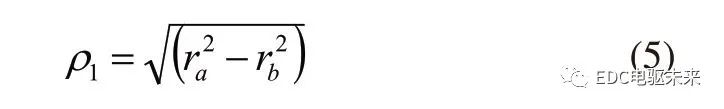
2）計算嚙合最低點的最小曲率半徑：

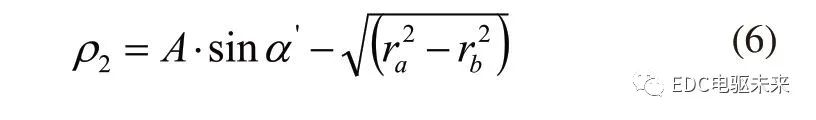
3）計算齒頂和齒根修緣量δ：

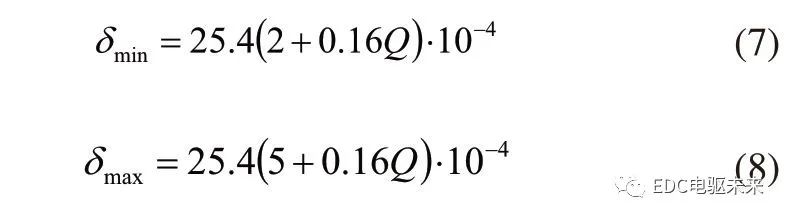
4）齒輪修形起始點：

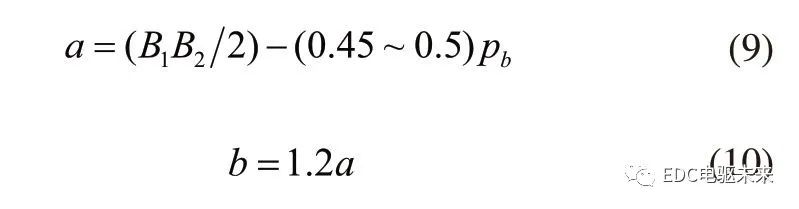
其中：

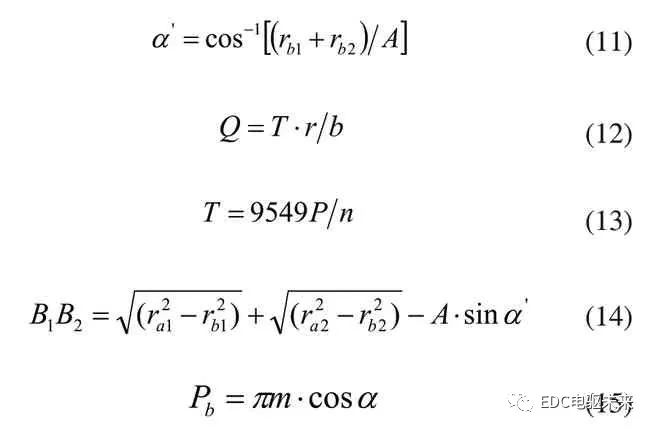
式中，ra、rb分別為齒輪齒頂圓半徑和分度圓半徑，A為兩嚙合齒輪副的中心距，a'為齒輪副嚙合壓力角，Q為單位齒寬上的作用力，b為齒寬，T為扭矩，P為功率，n為轉速，B1B2為齒輪副有效嚙合長度，Pb為基節，m為模數。

表2 最優一組修行量參數

為了清晰了解同一位置不同修形方式和不同位置同一修形方式對傳遞誤差、最大法向剛度、最大切向剛度以及最大應力的影響，采用圖形化方式進行比較，具體如圖10～圖13所示。

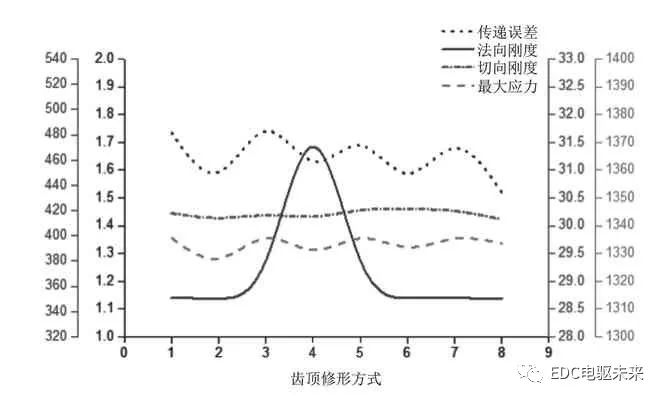
圖10 齒頂修形情況對比圖

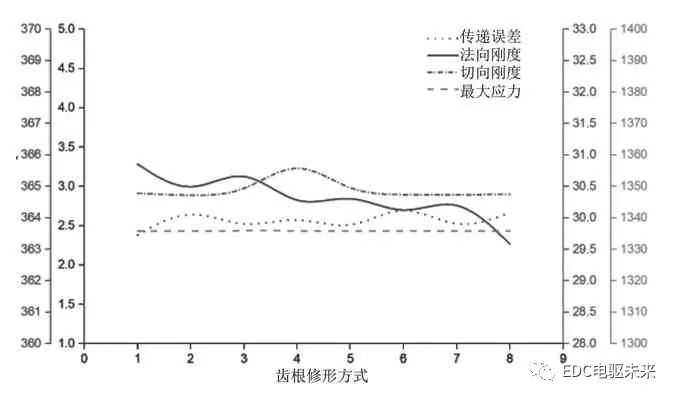
圖11 齒根修形情況對比圖

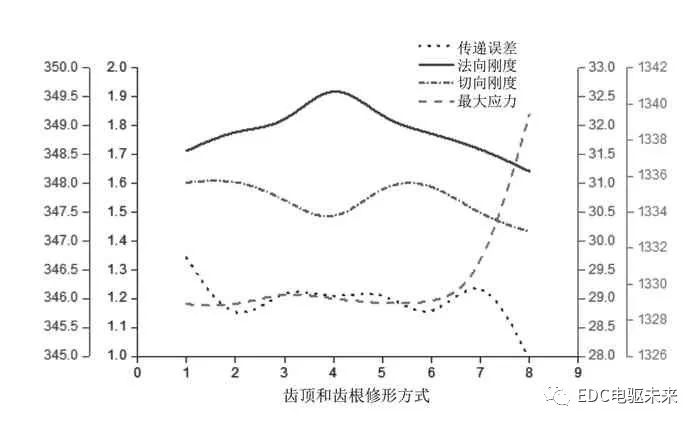
圖12 齒頂和齒根修形情況對比圖

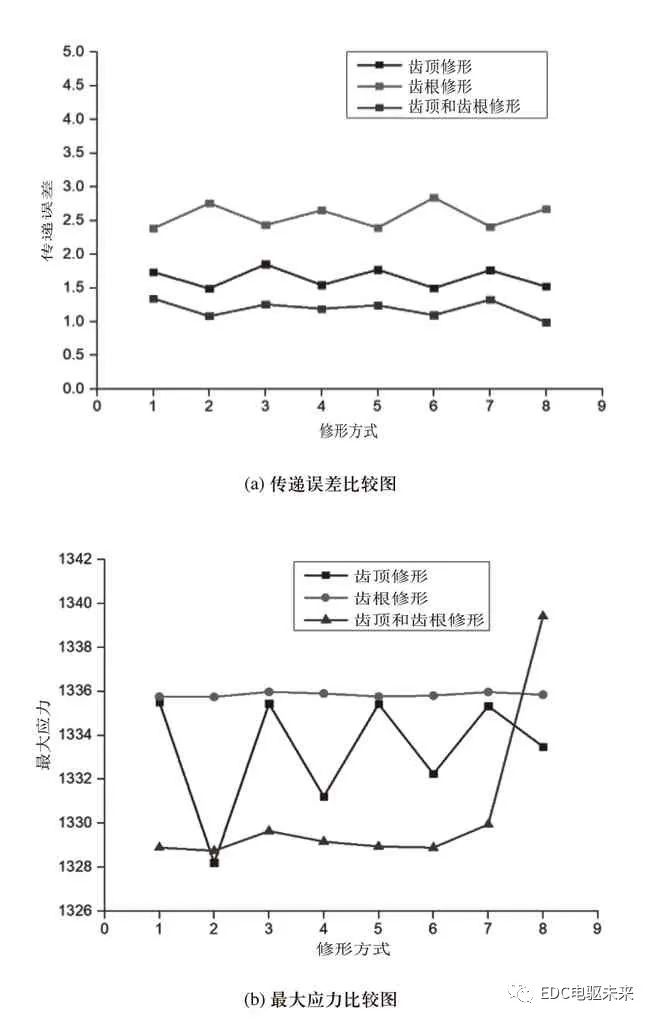
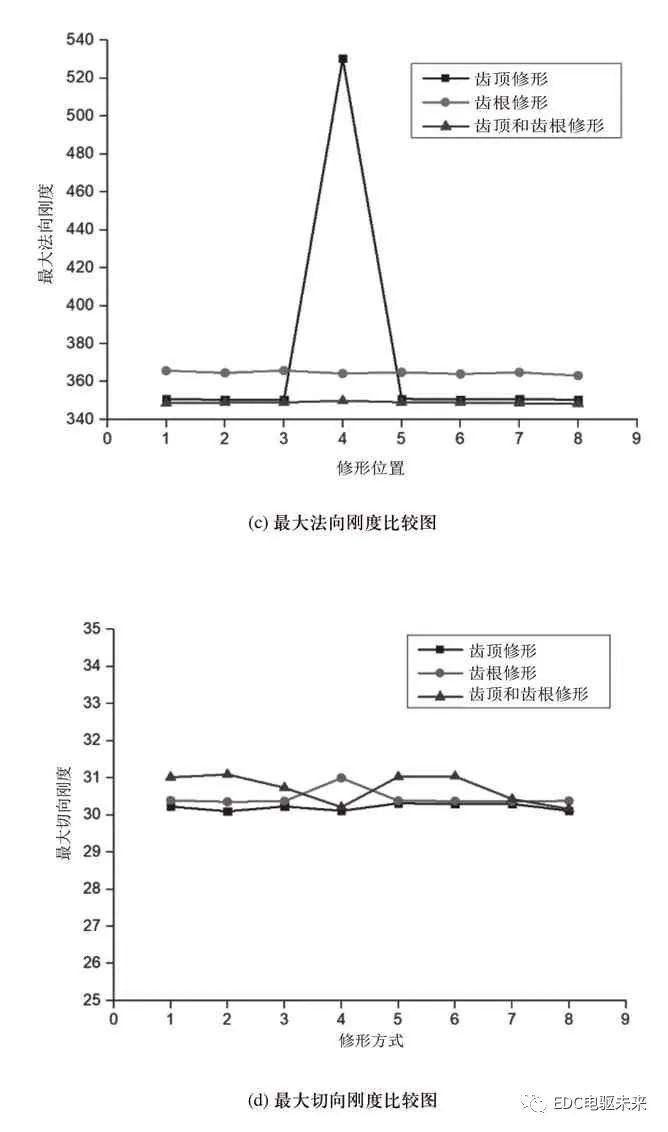
圖13 同一位置不同方式下的修形結果

圖13中，橫坐標1-9分別代表不同的修形方式，即1-短齒廓、2-長齒廓、3-短圓弧、4-長圓弧、5-短漸開線、6-長漸開線、7-短廓圓弧過渡、8-長齒廓圓弧過渡。

通過對上面圖表分析，結合實驗過程中得到的有關數據，可得出如下結論：

長齒廓修形較短齒廓修形效果更好，同時對齒頂和齒根同時進行修形時其傳遞誤差、最大應力以及最大法向剛度最低。其中，又以齒頂和齒根進行長圓弧修形時效果最佳，噪音最低。如圖14～圖16所示，這種修形方式下，傳遞誤差由初始的1.847μm減小至1.192μm，降低了35.5%；未修形前的法向剛度365.8582N/μm，切向剛度為30.3627N/μm，修行后法向剛度降為343.8746N/μm，切向剛度降為30.3092N/μm；未修形前齒面載荷沿齒寬方向分布不均，存在一定的偏載現象，最大載荷為1335.547N/mm2，修行后齒面載荷沿齒寬方向分布均勻、基本不存在偏載現象，最大載荷為1129.163N/mm2。

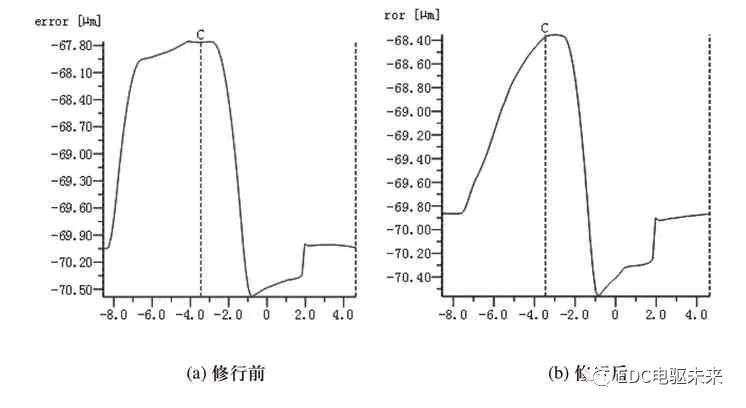
圖14 傳遞誤差曲線圖

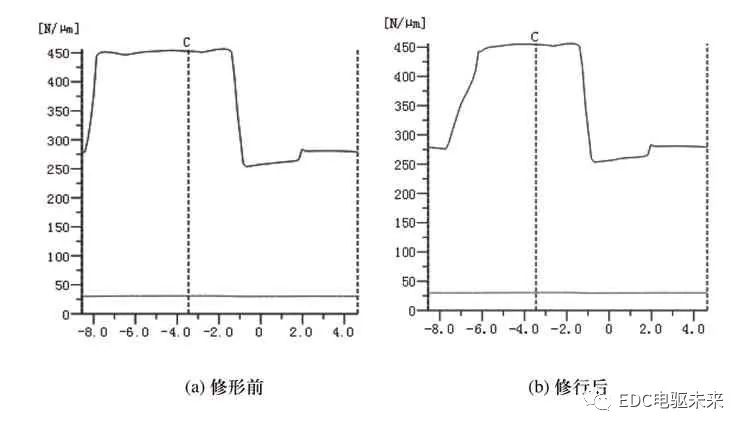
圖15 剛度曲線圖

圖16 齒面接觸載荷及分布圖

3 結語

本文在SolidWorks軟件中建立了漸開線變位直齒輪行星輪系的精確模型，之后導入Kisssoft軟件中進行仿真分析，通過不同修形方法及組合，分析修形前后行星輪系的傳遞誤差、齒面載荷分布及接觸斑點，得到最優的修形方法。通過對某型號的行星減速機的仿真分析，得出當對行星輪系的行星輪進行齒頂和齒根長圓弧修形時效果最好，其傳遞誤差、最大載荷及接觸斑點都得到相應的降低和優化，達到了減振、降噪的目的。因此，利用Kisssoft軟件對齒輪修形時，可大大提高齒輪修形的設計效率、減少設計周期。

題外話

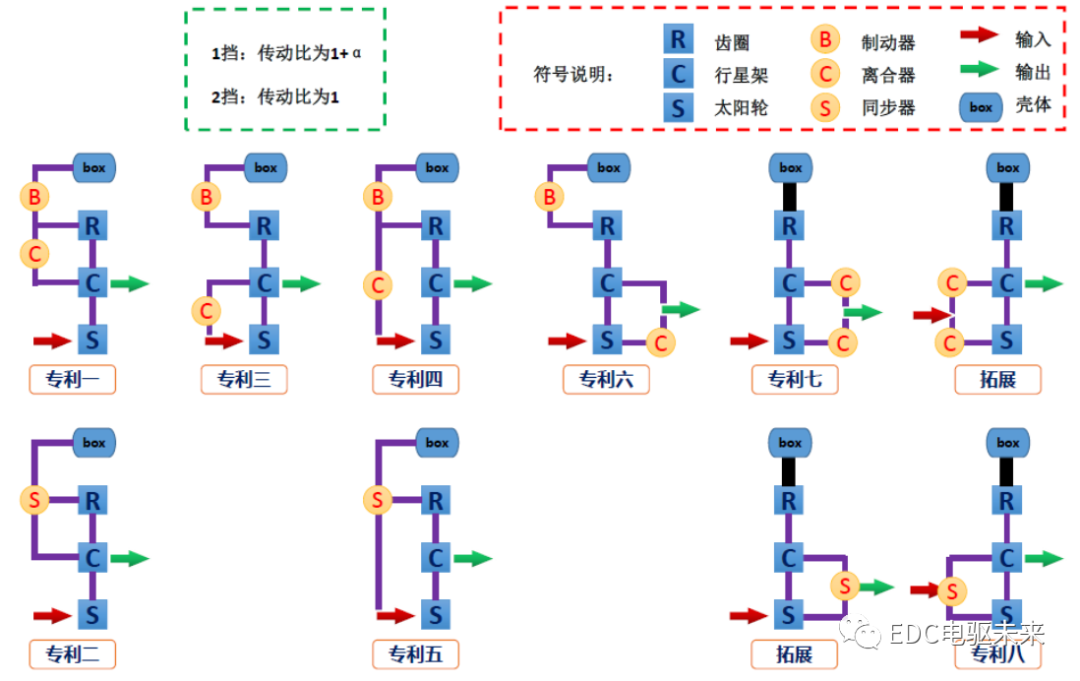
根據近年專利梳理來看，可以得出以下幾點經驗：

1、關于齒圈的固定，可以采用制動器實現接合與分離，也可以采用直接固定的方式；

2、其主要換擋元件可采用制動器和離合器的組合使用，布置在不同的位置；

3、當某一元件為共用元件時，可采用同步器替換制動器和離合器的組合；

4、當齒圈直接固定在殼體上時，可在輸入端采用換擋元件對動力路徑的選擇，也可以在輸出端對動力路徑進行選擇。

審核編輯：湯梓紅