本文將介紹基本控制理論,并討論如何分析DC-DC電壓控制環路的穩定性和帶寬。它可以幫助設計人員深入了解控制環路,以及在遇到控制環路問題時準確快速地計算電路參數,而不是反復試驗。
介紹
環路補償是設計DC-DC轉換器時的關鍵程序。如果應用中的負載具有高動態范圍,設計人員可能會發現轉換器不再平穩工作,輸出電壓不再穩定,從而導致穩定性或帶寬問題。了解環路補償概念有助于設計人員處理典型的電源管理應用。
本文分為三個部分。前兩部分討論控制系統理論、一般降壓DC-DC轉換器拓撲以及如何設計DC-DC控制環路。在第三部分中,我們以MAX25206為例,說明如何應用控制理論來評估和設計DC-DC控制環路。
控制系統理論簡介
控制系統無處不在。空調控制室溫,司機控制汽車的方向,蒸籠控制煮餃子時的溫度等。控制是指操作一個裝置或一個物理量生產過程,實現一個變量來保持恒定,或者沿著預設軌跡沿預設軌跡運動的動態過程。通常,自然界中的系統是非線性的,但微觀過程可以被視為線性系統。在半導體領域,我們將微電子視為線性系統。
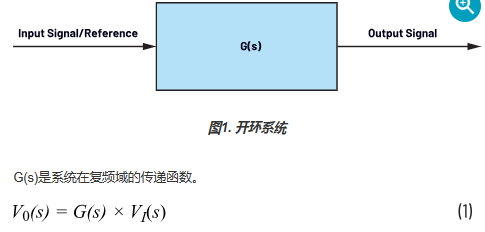
能夠實現自動控制的系統是閉環系統,反之則是開環系統。開環系統的特點是系統的輸出信號不影響輸入信號。如圖 1 所示,其中
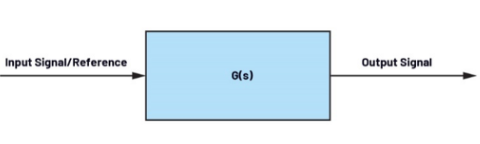
圖1.開環系統。
G(s)是系統在復頻域中的傳遞函數

VI是輸入信號,VO是s域中的輸出信號。圖2中的閉環系統具有從輸出到輸入的反饋路徑。系統的輸入節點將是輸入信號和反饋信號之間的差值。

圖2.閉環系統。
當控制器迭代直到輸入信號等于反饋信號時,控制器達到穩定狀態。使用數學方法,您可以得到以下閉環系統方程:

其分母相位(公式4)等效于開環傳遞函數(也稱為環路增益)。其增益幅度提供反饋強度,其帶寬是閉環系統的可控帶寬。當然,它們的相移也會疊加。應該知道,如果環路增益大于0 dB,同時相移為180°,則控制環路將以正反饋工作并形成振蕩器。這是穩定性設計的關鍵點。
設計人員應確保相位裕量和增益裕量在安全范圍內,否則整個系統環路將開始自振蕩。
通用降壓DC-DC轉換器拓撲
接下來,我們看一下降壓DC-DC轉換器的拓撲和控制環路。

圖3.降壓直流至直流模塊。
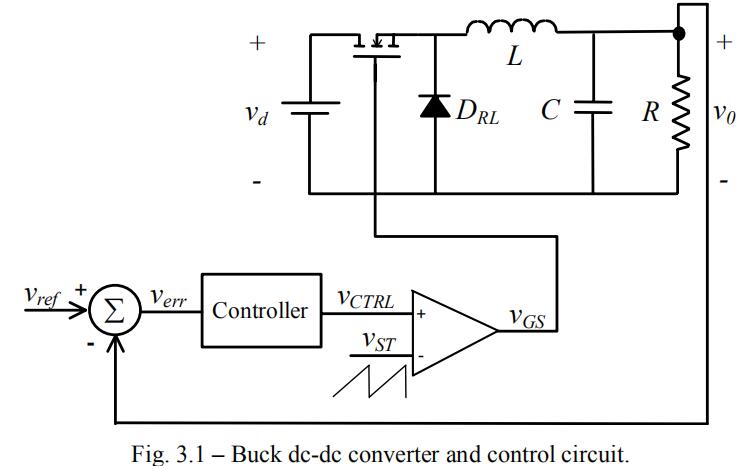
圖3所示為簡化為小型交流信號電路的典型降壓轉換器原理圖。它包括三級:降壓調制器級、輸出LC濾波器級和補償網絡級。每個階段都有自己的傳遞函數。
這三個階段構成了整個控制回路。比較器和半橋構成降壓調制器。比較器輸入信號來自振蕩器和補償網絡。補償網絡在閉環反饋路徑中實現。調制器的交流小信號增益為

其中VPP是振蕩器三角波的峰峰值電壓。VCC是半橋的輸入功率。在控制理論中,小信號增益等效于傳遞函數。如您所見,調制器沒有相移,只有幅度增益。LC濾波器傳遞函數為

其中L和C是電感和電容。這是一種理想的狀態。通常,電路中存在寄生參數,如圖4所示。

圖4.具有寄生參數的LC濾波器。
DCR 是電感 L 的直流等效電阻,ESR 是輸出電容器的等效串聯電阻。因此,LC濾波器傳遞函數為

顯然,ESR將為控制環路生成零。當ESR太大而無法忽略時,設計人員應考慮ESR可能導致的穩定性問題。補償網絡用于消除寄生效應并改善環路響應。

圖5.II類補償拓撲。
降壓DC-DC模塊向我們展示了一個II型補償網絡。這種補償電路將提供一個零點和兩個極點。
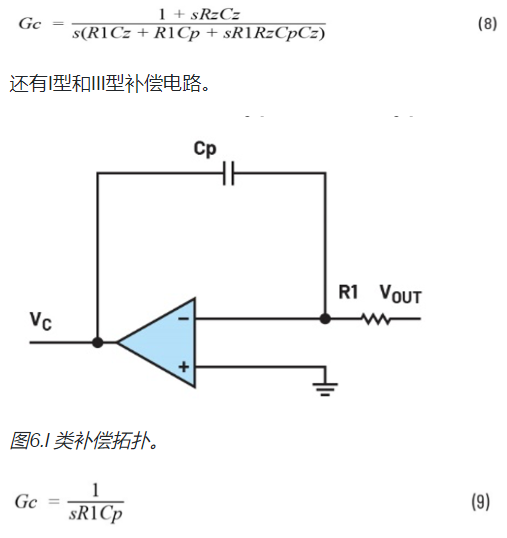
類型 I 只是一個集成節點。這是一個最小相位系統。

圖7.III型補償拓撲。
III型傳遞函數類似于II型傳遞函數。

如您所見,III型傳遞函數更為復雜。它有兩個零和三個極點。在圖7中,運算放大器(OPA)用于誤差放大。運算跨導放大器(OTA)也可用于環路中的誤差放大。

圖8.具有 OTA 的 II 類補償拓撲。
它的傳遞函數類似于 OPA 拓撲。輸出電壓誤差信號首先通過OTA放大并轉換為電流信號,然后通過補償網絡轉換為電壓控制信號。在選擇的任何類型的拓撲或放大器中,零點和極點必須位于適當的頻率。
如何設計DC-DC控制回路?
讓我們看一下具有II型環路補償的降壓DC-DC轉換器的整個開環傳遞函數。

調制器和LC濾波器的傳遞函數不能輕易改變。
我們只能修改補償網絡。
讓我們以類型 II 拓撲為例。II型傳遞函數有兩個極點和一個零點,如下所示。
Fz = 1/RzCz;
Fp1 = 0;
Fp2 = R1(Cz + Cp)/R1RzCpCz;
極點和零點位置由環路增益和環路相移決定。正極點將為波特圖中的增益曲線增加–20 dB/dec斜率,并將為波特圖中的環路相位曲線增加–90°相移。相反,正零點將為增益曲線增加20 dB/dec斜率,并為環路相位曲線增加90°相移。我們可以看到,對于II型補償環路,有兩個極點和一個零點,具有寄生效應的LC濾波器也有2個極點和一個零點。寄生極點可能會迫使環路增益交越點(開環圖與軸交叉的點;其中增益為0 dB)的斜率高達-40 dB/dec甚至更高。這意味著系統的相移將達到180°(相位裕量將達到0°)并引起自振蕩。設計師應該避免這種風險。根據經驗,我們應該確保環路增益交越斜率為–20 dB/dec。為了解決這個問題,設計人員只能修改補償網絡。修改Rz或Cz可以改變零的位置,修改Cp可以修改子極點。通常,寄生極點和零點位于非常高的頻率中,因此我們將Fp2放置在比Fz稍遠的位置,以強制寄生極點和零點低于0 dB。Fz和Fp2都將是環路帶寬的重要
因素。

圖9.II型波特圖。
通過調整極點和零點的位置,可以改變環路的頻率響應和相位響應。
因此,我們可以在環路帶寬和穩定性裕度之間實現平衡。
例如,MAX25206的原理圖如圖10所示。在該電路中,VOUT = 5 V,ILOAD = 3.5 A,因此RLOAD = 1.43 Ω。

圖 10.MAX25206典型原理圖
其補償網絡是Cp = 0 pF的II型網絡(根據公式8)。第二個極點位于無窮大頻率處,我們可以計算出 R5 和 C2 的第一個零點,Fz = 1/(4.7 nF × 18.2 kΩ) = 11.69 kHz。在輸出LC濾波器中,我們可以通過傳遞函數方程7在Fz = 16.4 MHz時以及Fp1 = 1.8 kHz –37.6 kHz和Fp2 = 1.8 kHz + 37.6 kHz時的復極點得到ESR和輸出電容的零點。可以預見的是,Gf增益將在1.8 kHz時達到最大點。當頻率大于1.8 kHz時,Gf增益將迅速下降。補償零Fz是對環路增益降低的補償。此外,我們應該知道,如果環路增益大于0 dB,LC濾波器將以37.6 kHz諧振。設計人員不應將Fz設置得太接近1.8 kHz,以確保環路增益在37.6 kHz時不會高于0 dB。交流環路仿真結果如圖11所示。
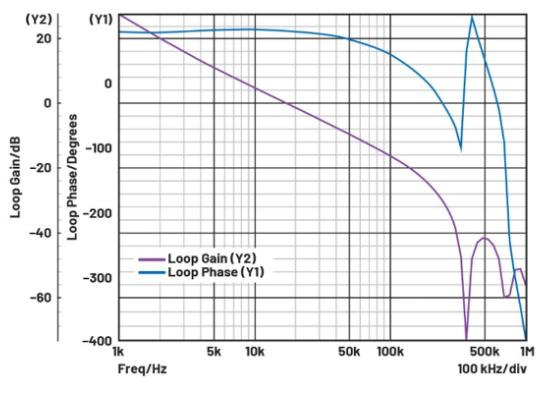
圖 11.MAX25206交流環路仿真
此外,Type III可以提供更大的環路帶寬和穩定性潛力。當然,要評估一個系統,我們不僅應該使用開環傳遞函數和波特圖,還應該觀察閉環傳遞函數的根軌跡是否在左半平面,并在時域中分析微分方程。但就便利性而言,觀察波特圖的開環傳遞函數是實現穩定電源系統設計的最常見和最簡單的方法。補償環路、補償方法和理論與其他類型的DC-DC拓撲相同。
唯一的區別是調制器,它只是環路傳遞函數的增益。
其他補償網絡拓撲示例
除了不同類型的DC-DC拓撲外,還有具有不同方案的控制環路。與DC-DC轉換器一樣,MAX20090LED控制器由電流控制環路組成。轉換器檢測輸出電流并將其反饋回控制環路以達到預期值。另一個例子是MAX25206降壓控制器,具有限制峰值或平均電流的功能。它檢測輸出電壓和平均電流并反饋它們。它是一個雙閉環控制器。通常,電流控制環路在內環路中,電壓控制環路在外環路中。電流環路的帶寬(即響應速度)大于電壓環路的帶寬,因此可以實現限流。第三個例子是MAX1978溫度控制器。它包含一個驅動熱電冷卻器(TEC)的H橋。不同電流的方向將決定TEC的加熱或冷卻模式。反饋信號是TEC的溫度。這樣的控制環路將迫使輸出TEC的溫度達到預期溫度。
結論
無論哪種形式的電路拓撲結構,用于自動控制的模擬電路的基礎是本文討論的理論。設計人員的目標是實現更高的帶寬和更魯棒的穩定性,同時平衡環路帶寬和穩定性。
審核編輯:郭婷
-
轉換器
+關注
關注
27文章
8742瀏覽量
147749 -
控制系統
+關注
關注
41文章
6657瀏覽量
110792
發布評論請先 登錄
相關推薦
DCDCCONV(DC-DC轉換器)是什么
DC-DC轉換器控制回路分析
什么是DC-DC轉換器?DC-DC轉換器是如何命名的?

什么是控制系統以及如何設計DC-DC轉換器的控制回路
一文了解控制系統及DC-DC轉換器控制環路設計推薦





 什么是控制系統以及如何設計DC-DC轉換器的控制回路
什么是控制系統以及如何設計DC-DC轉換器的控制回路










評論