<問題描述>
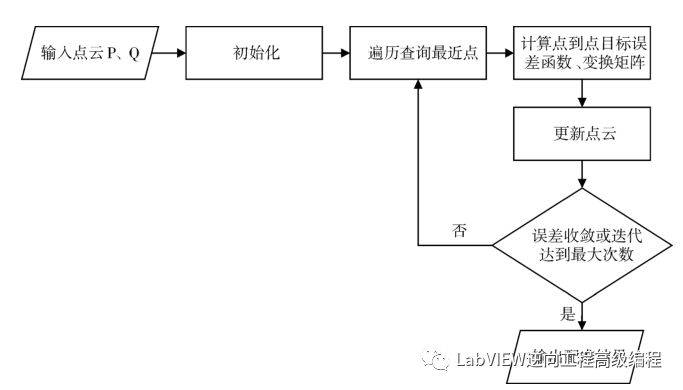
傳統(tǒng)經(jīng)典的方法就是ICP算法,Besl于1992年提出,稱為ICP(最近點(diǎn)迭代算法)。該方法將輸入的兩片點(diǎn)云分別記為源點(diǎn)云P和目標(biāo)點(diǎn)云Q,通過遍歷搜索找到P、Q之間所有點(diǎn)的對應(yīng)關(guān)系得出變換矩陣H,最后以兩點(diǎn)距離的平方和作為目標(biāo)誤差函數(shù),不斷迭代計算,直至滿足一定的誤差收斂條件。
這個問題在很多方面都會遇到,比如相機(jī)的外參標(biāo)定,在世界坐標(biāo)系放置幾個點(diǎn),相機(jī)a在自己的坐標(biāo)系下面看到的坐標(biāo)是a1,a2,a3...an,相機(jī)b在自己坐標(biāo)系下面看到的是b1,b2,b3...bn,如何將將相機(jī)a兩個相機(jī)統(tǒng)一到a的坐標(biāo)系下面。此時就會用到點(diǎn)的配準(zhǔn)。
使用三維掃描進(jìn)行物體掃描,要將一個物體完整的建模需要多個視角連續(xù)采集,每個視角相機(jī)的姿態(tài)都會存在變化,視角之間需要配準(zhǔn),通常的方法是在物體表面貼Marker點(diǎn),通過識別Marker點(diǎn)的坐標(biāo),快速配準(zhǔn)然后再局部優(yōu)化。
Nonlinear Curve Fit 最適合輸入數(shù)據(jù)點(diǎn)集(X,Y)的參數(shù)集,如非線性函數(shù)Y=f(X,a)所示,其中a是參數(shù)集。該方法使用Levenberg-Marquardt(列文伯格-馬夸爾特)算法,是使用最廣泛的非線性最小二乘算法。
使用這個函數(shù)來優(yōu)化迭代找到最優(yōu)的變換矩陣,核心是設(shè)置這個迭代的VI。
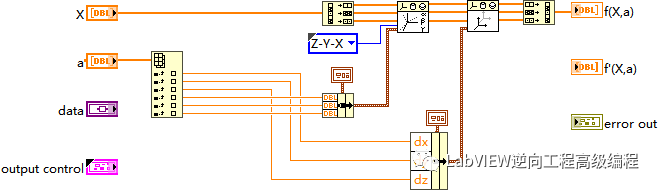
輸入點(diǎn)先進(jìn)行旋轉(zhuǎn)計算,再進(jìn)行平移計算,最后輸出變換后的點(diǎn)集,通過迭代使得輸出變換后的點(diǎn)集Q與目標(biāo)點(diǎn)集P的差值最小。
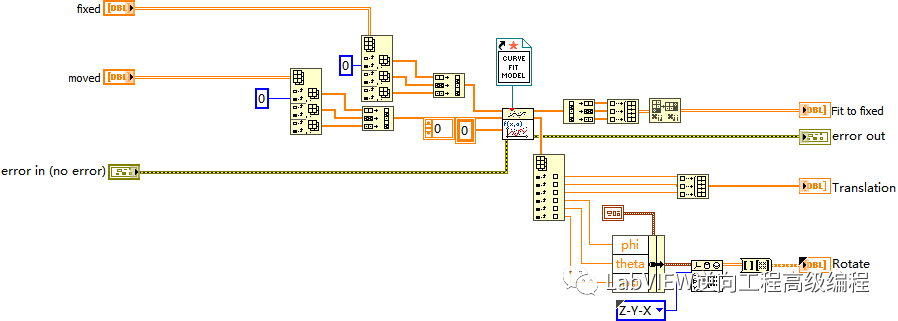
將源點(diǎn)云和目標(biāo)點(diǎn)云變換為1D數(shù)組,通過Nonlinear Curve Fit 迭代,最后輸出變換后的RT(旋轉(zhuǎn)矩陣和平移向量)。
<結(jié)果驗證>
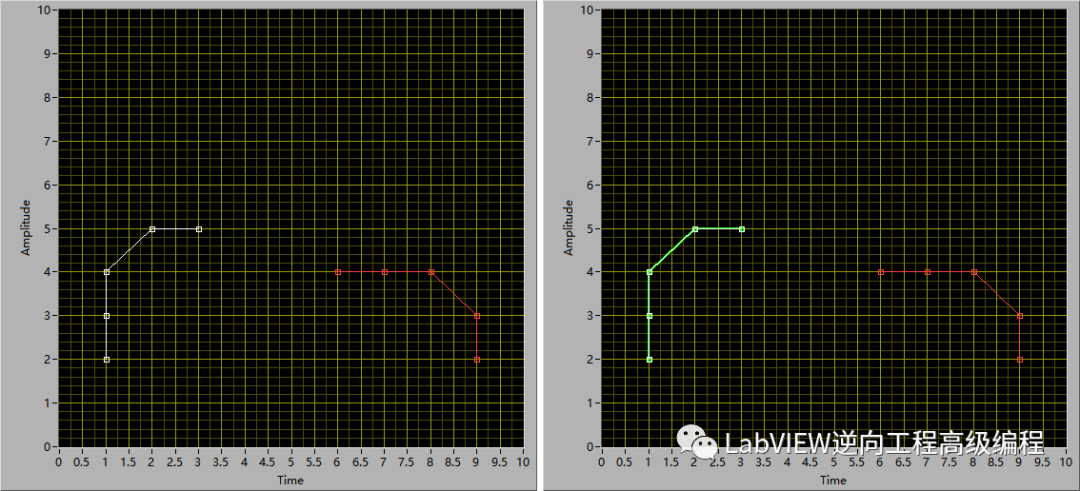

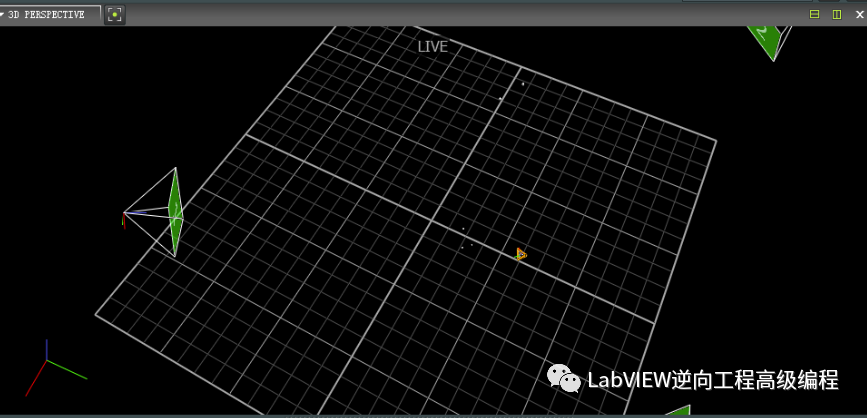
白色點(diǎn)是源點(diǎn)云P,紅色線是目標(biāo)點(diǎn)云Q,綠色線是配準(zhǔn)后的Q,結(jié)果配準(zhǔn)后的Q與源點(diǎn)集P重合。
這里提供了一種類似于ICP算法的一種方法,希望對大家有所啟發(fā)!
審核編輯:劉清
-
LabVIEW
+關(guān)注
關(guān)注
1976文章
3657瀏覽量
325062 -
ICP算法
+關(guān)注
關(guān)注
0文章
2瀏覽量
980
原文標(biāo)題:基于LabVIEW的三維點(diǎn)自動配準(zhǔn)
文章出處:【微信號:gh_63f7cd07072a,微信公眾號:LabVIEW逆向工程高級編程】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
基于深度學(xué)習(xí)的三維點(diǎn)云配準(zhǔn)方法
機(jī)器視覺之ICP算法和RANSAC算法
基于角點(diǎn)的紅外與可見光圖像自動配準(zhǔn)方法
一種快速的三維點(diǎn)云自動配準(zhǔn)方法
計算機(jī)視覺中的ICP算法
三維顱骨自動非剛性配準(zhǔn)方法
基于平移域估計的點(diǎn)云全局配準(zhǔn)算法

耳廓三維網(wǎng)格去補(bǔ)丁合并算法
基于分層策略的三維非剛性模型配準(zhǔn)算法

使用PCL進(jìn)行點(diǎn)云數(shù)據(jù)粗配準(zhǔn)算法的研究資料分析
一種多幅點(diǎn)云數(shù)據(jù)與紋理序列自動配準(zhǔn)方法





 一種類似于ICP算法的三維點(diǎn)自動配準(zhǔn)方法
一種類似于ICP算法的三維點(diǎn)自動配準(zhǔn)方法











評論