?先討論濾波器的概念，濾波的意思是，讓機器人在某個正確位置上對應的概率越高越好。

也就是可以理解為：把錯誤位置上的概率濾低，把正確位置處的概率濾高。

假設一個機器人小R在如下場景中出現，他剛開始不知道自己在哪（小R還沒看到他眼前的門），因此他在這個場景中任何位置的概率是相等的。

如果此時縱坐標為機器人小R在對應位置處的概率，橫坐標表示各個位置，應該是一條均勻分布的直線。

突然，機器人看到了眼前這個門，這里假設機器人提前知道一共有三個門，因此小R現在知道自己可能在任意一個門前，即三個門分別對應著一個正態分布。此時的概率波形可以理解為先驗概率。

小R繼續向前走到第二個門前，他通過自己身上安裝的里程計發現自己走了d個單位。

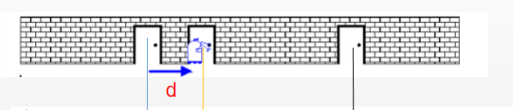
根據之前的概率分布，小R可以預測到，自己的位置應該向右平移了d個單位。那么可以將之前的概率分布向右平移d個單位，得到此時通過傳感器得到的概率分布。此時的概率波形可以理解為似然概率。

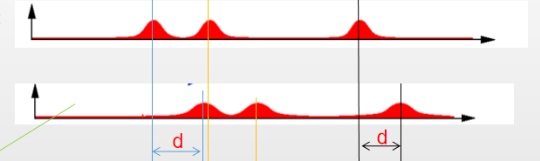
小R突然發現自己看到了第二扇門前，僅根據當前的觀測，小R知道自己在三個門前的概率相同，又可以得到之前的三個正態分布。根據傳感器預測得到的分布和根據先驗信息得到的分布得：

兩個波形信號可以做個卷積融合得到：

這樣小R在第二扇門處（正確位置）的概率就變大了，在其他位置處的概率就變小了，進而達到了濾波的目的。

以上即是普通濾波器的直觀解釋，同樣地，可以類比到卡爾曼濾波上。

由式(2)可知，新的不確定性由上一時刻不確定性預測得到，并加上外部環境的干擾。

這時我們對系統的變化有了模糊的估計，更新的狀態（均值）和不確定性（協方差）分別如式(1)和(2)，預測的過程相當于之前的波形向右平移d個單位的過程。

得到的新的最優估計可以放到下一時刻不斷迭代。以上就是經典卡爾曼濾波器的五個公式，給出了線性高斯系統的最優無偏估計。

我們可以用這些公式對任何線性系統建立精確的模型，對于非線性系統來說，我們使用擴展卡爾曼濾波，區別在于EKF多了一個把預測和測量部分進行線性化的過程。

此時再看這個高贊無公式推導的回答來回顧全局，一切豁然開朗

無公式直白解釋卡爾曼濾波：

假設你有兩個傳感器，測的是同一個信號。可是它們每次的讀數都不太一樣，怎么辦？
取平均。

再假設你知道其中貴的那個傳感器應該準一些，便宜的那個應該差一些。那有比取平均更好的辦法嗎？
加權平均。（乘卡爾曼增益 K）

怎么加權？假設兩個傳感器的誤差都符合正態分布，假設你知道這兩個正態分布的方差，用這兩個方差值，（此處省略若干數學公式），你可以得到一個“最優”的權重。

接下來，重點來了：假設你只有一個傳感器，但是你還有一個數學模型（指的是上文中的預測模型）。模型可以幫你算出一個值，但也不是那么準。怎么辦？

把模型算出來的值，和傳感器測出的值，（就像兩個傳感器那樣），取加權平均。

OK，最后一點說明：你的模型其實只是一個步長的，也就是說，知道x(k)，我可以求x(k+1)。

問題是x(k)是多少呢？答案：x(k)就是你上一步卡爾曼濾波得到的、所謂加權平均之后的那個、對x在k時刻的最佳估計值。于是迭代也有了。這就是卡爾曼濾波。（無公式）