1從基礎卡爾曼濾波到互補卡爾曼濾波
卡爾曼濾波自從1960被Kalman發明并應用到阿波羅登月計劃之后一直經久不衰,直到現在也被機器人、自動駕駛、飛行控制等領域應用。基礎卡爾曼濾波只能對線性系統建模;擴展卡爾曼濾波對非線性方程做線性近似以便將卡爾曼濾波應用到非線性系統。后來研究者發現將系統狀態分成主要成分和誤差,并將卡爾曼濾波用來預測誤差,會使得系統的近似程度更高,效果更好。在姿態解算任務中,研究者們用輔助傳感器如加速度計和磁力計來修正角速度計的積分結果,得到互補卡爾曼濾波的形式。 卡爾曼濾波是一種工具,對實際問題的不同建模方式會得到不同形式的卡爾曼濾波器。這導致了對于初學者不知道從何看起是好。另外也似乎很少有文章對基礎卡爾曼濾波到各種形式的濾波形式做總結說明,于是便有了這篇文章。本文會從以下幾個方面分析和講解多種卡爾曼濾波器形式:
基礎卡爾曼濾波——對線性系統的預測
擴展卡爾曼濾波——基礎卡爾曼濾波在非線性系統的擴展
基于四元素的卡爾曼濾波器——基于實際問題的講解
狀態誤差卡爾曼濾波——將狀態誤差引入狀態向量
互補卡爾曼濾波——一種只使用角度誤差和角速度誤差作為狀態向量和測量向量的濾波器形式
2符號定義
小寫字母為變量;加粗小寫字母為向量;大寫和加粗大寫為矩陣
3基礎卡爾曼濾波器
宏觀認識
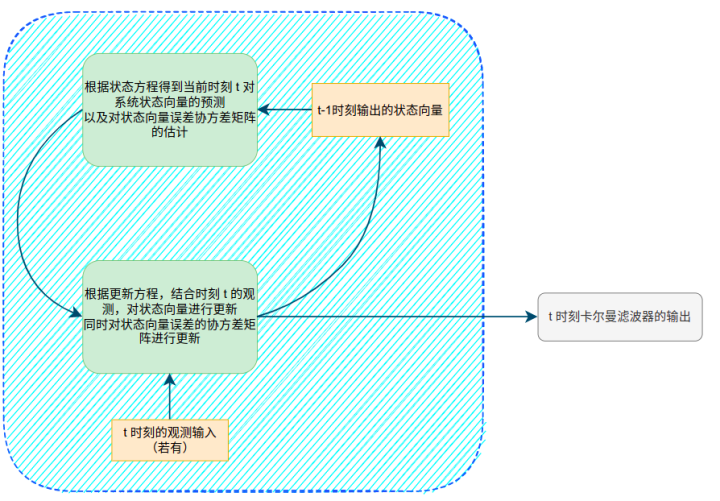
卡爾曼濾波包含兩個步驟
預測(prediction)—— Dynamic model
更新(correction/measurment update)—— Observation model
所謂預測,就是用一個數學模型,根據當前的傳感器輸入,直接計算此時系統的狀態。可以理解為一個方程的計算就行。 所謂的更新,就是在某些時刻或者每一時刻,獲取一些系統的其他狀態輸入(我們將這個值叫做測量值),比較此刻預測的系統狀態和測量的系統狀態,對預測出的系統狀態進行修正,因此也叫測量更新(measurment update)。 整體框架如下圖所示
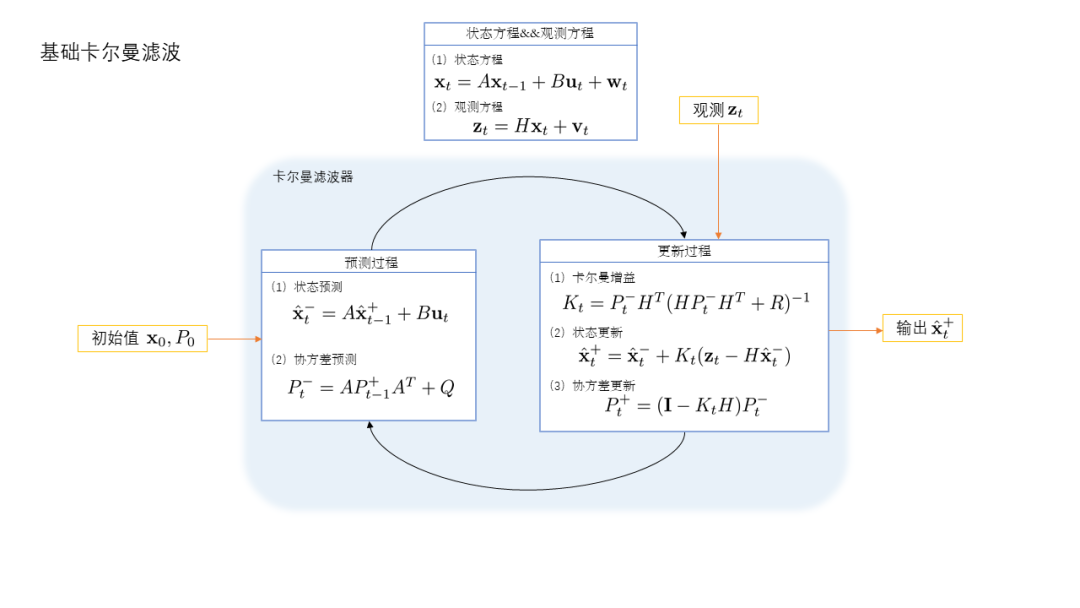
狀態方程及測量方程
其中是系統狀態向量,是測量向量。分別是過程噪聲和觀測噪聲,且滿足高斯分布 ? ?
預測過程
其中,是先驗狀態的誤差協方差矩陣 ?
更新過程
詳細公式推導
本文作為一篇概述性文章,為了不使篇幅過于冗長,不進行基礎卡爾曼濾波器公式的推導。想完全理解基礎卡爾曼濾波器可以參考下面這幾篇資料:
卡爾曼濾波基礎知識及公式推導——較為形象化地講解預測和更新這兩個過程之間地概率分布關系
wiki Kalman Filter——準確的公式化推導
如何理解卡爾曼濾波器?
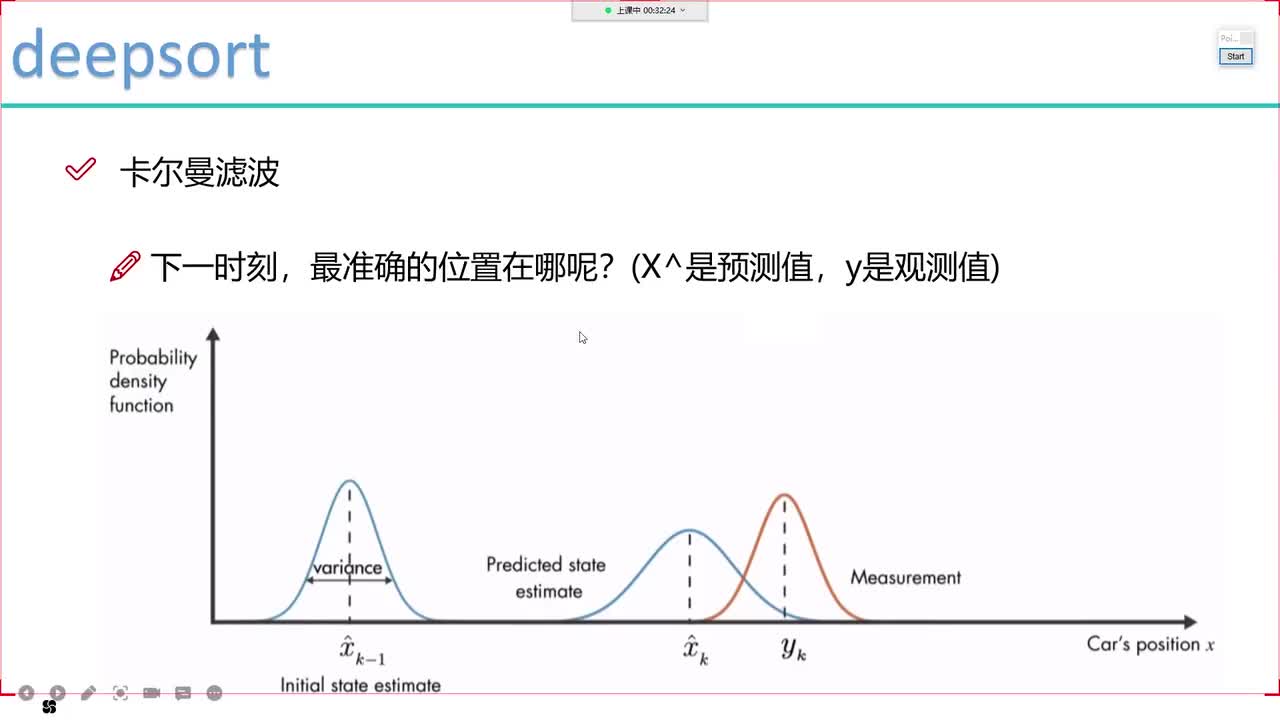
從概率分布的角度
卡爾曼濾波器將系統狀態的變化中的過程噪聲假設為均值為0的高斯噪聲,使得狀態向量也變為一個符合高斯分布的隨機向量。同時對觀測過程的噪聲也假設為均值為0的高斯噪聲。通過測量方程,即公式(1-2)得到將狀態向量映射到測量向量的函數。于是,當得到測量值的時候,可以利用測量值與狀態向量之間的關系得出另外一個對狀態向量的估計。利用測量值得出的狀態估計和狀態方程計算的狀態均符合高斯分布,兩個高斯分布的聯合概率分布依舊保持高斯特性。進一步推導可以得到公式(1-5)到公式(1-7)。關于這個角度的理解可以閱讀上面推薦的第一篇文章。
從最小化誤差的角度
卡爾曼濾波的最終輸出是,真實的狀態為,令 ? 對誤差的平方求最小值,同樣可以推導出公式(1-5)到公式(1-7)。因此卡爾曼濾波器也是系統狀態的最優估計。關于這個角度的理解和推導可以參考上面推薦的第二篇文章。
4擴展卡爾曼濾波
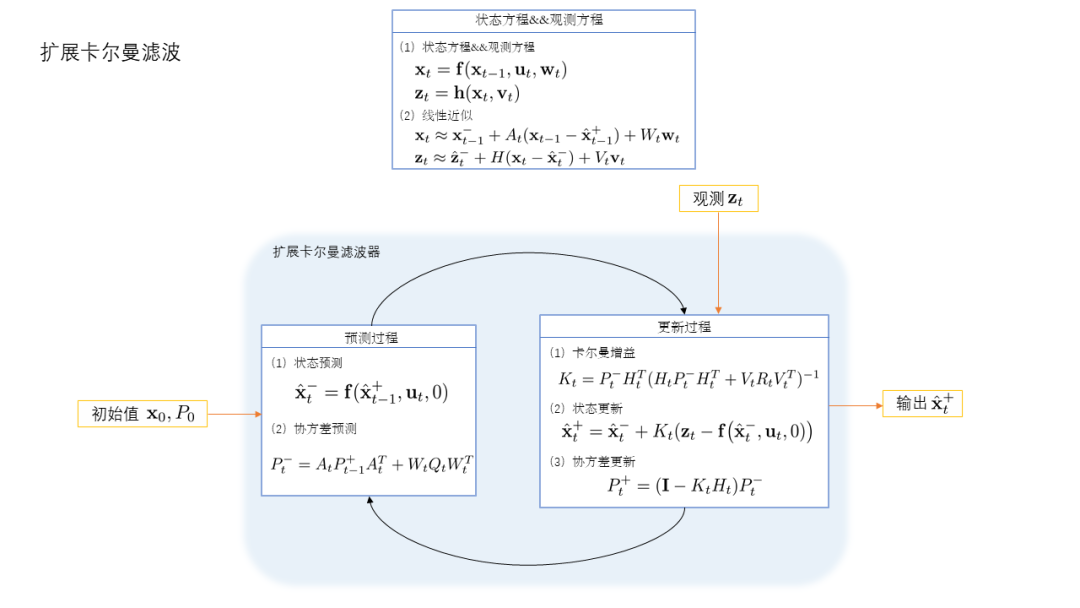
非線性方程的線性近似
卡爾曼濾波器建立在線性的狀態方程和測量方程也就是公式(1-1)和公式(1-2)。但是在實際應用中,更多的關系是非線形關系,比如如何從連續的角速度計算出車輛當前的姿態角等。為了能夠利用基本卡爾曼濾波器的預測和更新過程,對于非線性的狀態方程和觀測方程,我們利用一階的泰勒展開,將非線性公式近似為線性公式。
狀態方程及測量方程
公式(2-1,2-2)可以類比基礎卡爾曼濾波器中的公式(1-1,1-2)
一階泰勒展開
我們先假設已知時刻濾波器的輸出,也就是時刻的狀態后驗,以及對應的協方差矩陣為 ? 同時,我們令的先驗為 ? 對公式(2-1)在這一點做展開,并只保留一次項 ? 同時,對公式(2-2)在這一點做泰勒展開,并只保留一次項 ? 在公式(2-4)和公式(2-5)中:
預測方程及狀態協方差矩陣
其中,公式(2-7)中的第二項,因為在線性近似方程(2-4)中,噪聲項滿足分布 ?
更新方程及卡爾曼增益
5基礎卡爾曼濾波器 && 擴展卡爾曼濾波器總結
?
6基于四元數的拓展卡爾曼濾波器
從實際問題講起
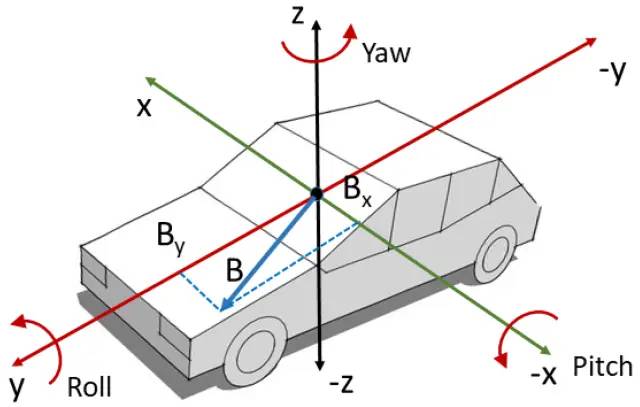
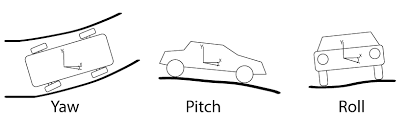
在運動物體的姿態估計,比如車輛的姿態計算中,常常利用IMU(Inertial Meseasurment Unit)慣性測量單元計算物體的姿態。為了方便敘述,這里的姿態估計意味著我們希望解算車輛在每一時刻與起始坐標系之間三個軸的偏轉角,通常用roll、pitch、yaw表示。
?
IMU(慣性測量單元)
現在的IMU一般是六軸或者九軸。六軸IMU可以輸出三個軸的加速度(acc)和角速度(gyro);九軸則在六軸的基礎上增加了磁力計(Magnetometer),測量三軸的磁場方向。為了簡化問題,我們用六軸IMU作為示例。
相關定義
在姿態估計的各個領域中,通常使用四元數來表示一個旋轉。四元數比歐拉角表達擁有更好的特性,同時相比于旋轉矩陣又更加緊湊。定義四元數如下 ? 為了估計系統的姿態,通常的做法是使用慣性測量單元IMU跟蹤角速度,我們另每一時刻的角速度為 ? 另外,我們需要知道IMU的輸出頻率。假設IMU的輸出時間間隔為
四元素乘積的導數
這部分是為了后面推導擴展卡爾曼濾波的狀態方程中的雅各比矩陣準備 我們令時刻的旋轉為.時刻的旋轉為。則的旋轉是時刻的旋轉經過的變化得到的,即 ? 其中等于在時間間隔內的角度變化量。在極短的時間間隔內,我們認為角度的變化是勻速的,也就是。我們令在這個時間間隔內,角度的旋轉軸為,旋轉角度為,則 ? ? 根據四元數的基礎知識,我們可以得到 ? 擴展卡爾曼濾波的重點之一在于求狀態方程相對于狀態的偏導;我們雖然可以從三軸角速度的輸出得出角度積分的離散形式公式(1),但是我們其實不能對其直接對求偏導。至于為什么不能直接求導,下面說得挺好:
求導的定義是函數值的微增量關于自變量的微增量的極限。表示旋轉的單位四元數作差后,其不再是單位四元數,也就不是旋轉四元數了
為了能夠對公式(1)求出偏導數,我們先求旋轉相對時間的導數。然后利用泰勒展開,將公式(1)展開為線性方程,并只取一次項,這樣就可以得到 ? 我們令 則 ? 有了角度相對于時間的導數之后,我們可以將公式(1)用泰勒展開 ? 只保留到一次項,則我們可以得到 ?
狀態向量及控制輸入
我們直接將車輛的姿態角以四元數形式表達作為系統狀態向量 同時,將每一時刻IMU的三軸角速度作為控制輸入
狀態方程及其雅各比矩陣
有了上一部分關于四元素導數的推導,我們可以直接寫出狀態方程如下 ? 其中是隨機噪聲,其協方差矩陣為
預測方程
由于在上面的推導中已經求出雅各比矩陣,所以預測方程可以直接根據拓展卡爾曼濾波公式寫出來 ? ?
測量更新
前文我們使用了角速度計的輸出作為控制輸入,并構建了狀態方程和預測方程。IMU通常都會有加速度計輸出,這部分輸出可以用來作為測量量,并對預測的狀態進行測量更新。我們先回顧測量更新中狀態向量的更新過程。 ? 令加速度計的輸出為測量向量:
測量模型
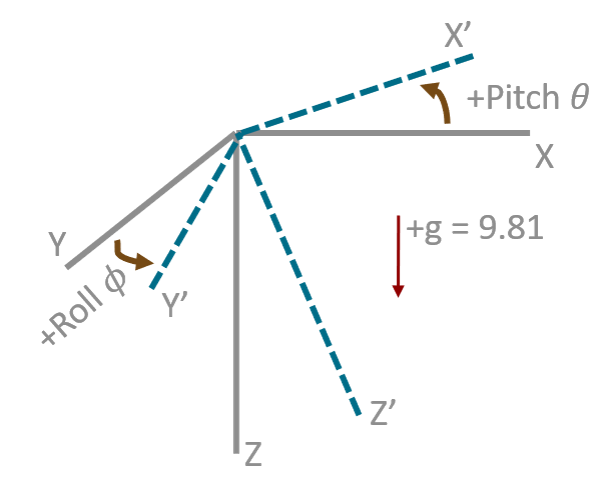
現在我們已經確定好了狀態向量為姿態角的四元數表達,測量向量為加速度計三個軸的輸出,那么函數要采用什么形式可以將姿態角轉成三軸加速度呢? 其中的關鍵聯系就是,當車輛靜止時,加速度的合向量是重力加速度,垂直向下!
上圖中,假設坐標系是起始坐標系,是小車移動后的坐標系。在起始時,小車靜止,小車的重力加速度的輸出是垂直向下的,即 ? 我們采用歸一化的形式,也就是將重力加速度當作一個單位。 則當小車運動后,重力加速度在坐標系下的表達為 ? 和是重力加速度在兩個不同坐標系下的表達,同時,這兩個坐標系之間的旋轉是此時的狀態向量,因此 ? 其中, ? ? 是將四元數轉成旋轉矩陣的表達,旋轉矩陣左乘一個三位的列向量表示將該向量進行三維旋轉。即下面的形式(是我們之前定義過的)
雅各比矩陣
從公式(3-7)我們可以得到測量模型中的轉換函數的雅各比矩陣
更新方程
7狀態誤差卡爾曼濾波器(ErKF : Error-state Kalman Filter)
概述
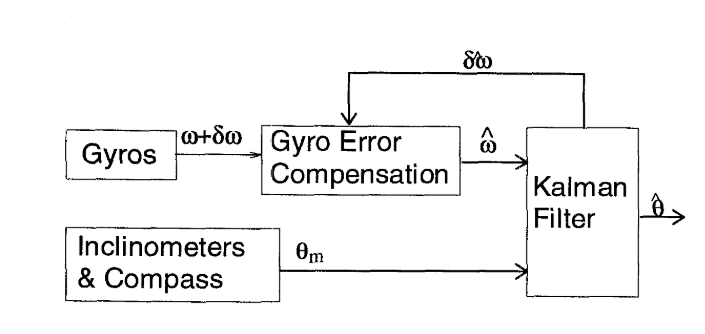
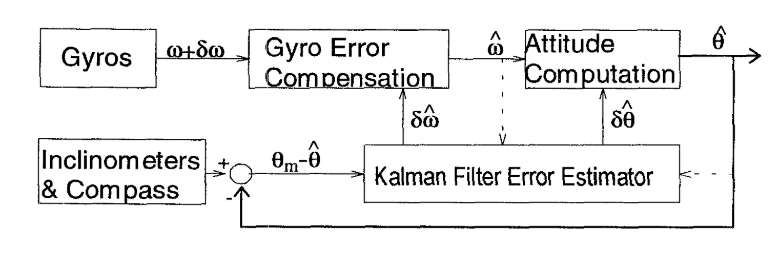
在使用卡爾曼濾波器做姿態估計(Attitude Estimation)中,很大一部分都采用不是直接將系統姿態角作為卡爾曼濾波的狀態,而是將姿態角的積分誤差和角速度計的誤差作為系統狀態。將角速度計的輸出彌補上估計出的角速度計誤差,然后對其積分,得到姿態角的估計,再彌補上姿態角的誤差估計。整個的流程圖大概如下面的圖,引用自Intertial Head-Tracker Sensor Fusion by a Complementary Separate-Bias Kalman Filter
PS: 要強調的是,各種卡爾曼濾波的形式多種多樣,同時各種符號的定義也都并不完全一致,這也是入門卡爾曼濾波比較難的地方,有時候找資料都不知道怎么找。這也是寫這篇文章的目的,提供一個基礎的脈絡給卡爾曼濾波的初學者。因此這里給出的ErKF只是形式之一,主要是引用自論文Extended Kalman Filter vs. Error State Kalman Filter for Aircraft Attitude Estimation
狀態誤差的遞推公式
首先,我們令表示時間連續形式的狀態向量。其相對于時間的導數為 ? 在等號的右邊輸入里加入微小擾動,同時,根據泰勒展開將函數展開 ? 則 ? 將上式使用離散形式表達 ? 即 ? 于是,有了狀態誤差的遞推公式,我們就可以像卡爾曼濾波一樣推導預測和更新過程
預測過程
與直接對系統狀態做卡爾曼濾波稍有不同,使用誤差狀態的卡爾曼濾波在計算姿態角的時候可以看成三步:
在卡爾曼濾波系統外使用積分算出此時的系統狀態
使用卡爾曼濾波算出此時系統狀態的誤差
將積分出來的系統狀態彌補上卡爾曼濾波計算出誤差
系統狀態計算
上式只是一個公式化表達,其實就是將上一時刻的狀態,在加上這一時間段狀態的變化量。姿態估計中,狀態的變化量通常是角速度計的輸出乘以時間間隔。
狀態誤差方程及預測方程
狀態誤差方程 由公式(4-1)可以得到狀態誤差的方程為 ? 其中,是過程噪聲,協方差矩陣為 預測方程 類似于普通卡爾曼濾波,預測方程為 ? ? ? ?
測量方程及更新方程
這里我們直接將使用其余傳感器如加速度計、磁力計計算出的姿態作為系統的測量量。在這里先記得,加速度計根據輸出的夾角可以計算出角,由磁力計可以計算出角即可。當然,也可以采用其他能夠直接輸出系統姿態角的傳感器作為測量值。 測量方程 ? 其中,是測量噪聲,協方差矩陣為 更新方程 這里要執行兩步更新
先更新對狀態誤差的估計
更新狀態的估計(即把狀態誤差彌補到)
補充
在上面的推導中,將我們的目標變量,即系統的姿態角作為外部一個單獨的積分計算,但是實際上更多的做法是將姿態角和角速度的偏差直接放在狀態向量中進行計算。然后對每一時刻的角速度偏差應用到角速度計的輸出,再將其作為系統輸入應用到狀態方程。也就是像概述中的圖示那樣。但是其實各種卡爾曼濾波的建模方式都不一樣,Error-state Kalman Filter和Complimentarty Kalman Filter也沒有嚴格的定義。所以索性這一章節當作對狀態誤差的理解和推導,在下面的互補卡爾曼濾波給出一種似乎是應用更廣泛的卡爾曼濾波器。
8互補卡爾曼濾波
前言
正如前文所說,卡爾曼濾波器的建模形式多種多樣,而且很多研究也是在上世紀,對于誤差狀態卡爾曼濾波(Error-state Kalman Filter)和互補卡爾曼濾波(Comlimentary Kalman Filter)其實沒有嚴格的定義。這里的互補卡爾曼濾波其實也可以看成上文ErKF的另一種形式。主要采用自論文Inertial head-tracker sensor fusion by a complementary separate-bias Kalman filter。卡爾曼濾波的工作太多,博客和論文也五花八門,看起來十分不易。這篇論文從引用、論文敘述、符號標識看起來都很不錯,很適合想要將卡爾曼濾波應用到姿態估計的工程師閱讀。甚至有一些工作,直接使用普通卡爾曼濾波輸出,然后利用互補濾波器的概念,在多種姿態輸出之間做加權平均,也叫互補卡爾曼濾波器,比如這篇專利:一種基于互補卡爾曼濾波算法計算融合姿態角度的方法
互補的概念
其實只要有了角速度計(Gyroscope)我們就可以根據其輸出,并在時間上做積分解算出車輛的姿態角。但是由于任何傳感器都是帶噪聲的,同時,直接用積分解算,誤差會隨機時間推移而累積,最終的姿態解算精度就非常差。除了使用角速度計進行積分可以得到姿態角之外,用加速度計(Accelerometer)和磁力計(Magnatometer)也可以計算出動態系統的姿態。其中,加速度計使用重力加速度作為錨定量,測量靜止狀態下三軸加速度之間的夾角,可以計算出角;磁力計(或叫地磁計)利用地球磁場北極作為錨定量,可以計算出角。使用這兩者對角速度計進行補充,可以得出更加準確的姿態估計。
從加速度計計算姿態角roll、pitch
加速度計(Accelerometer)可以輸出三個軸的加速度,在靜止的情況下,三個軸的合向量就是重力加速度。因此,我們可以利用三個軸加速度之間的關系計算靜止狀態下的俯仰角(pitch)和翻滾角(roll)
關于如何推導從三個軸的加速度計算roll和pitch,可以看這篇文章 最后得出的形式也非常簡單: ? ? ?
從磁力計計算姿態角yaw
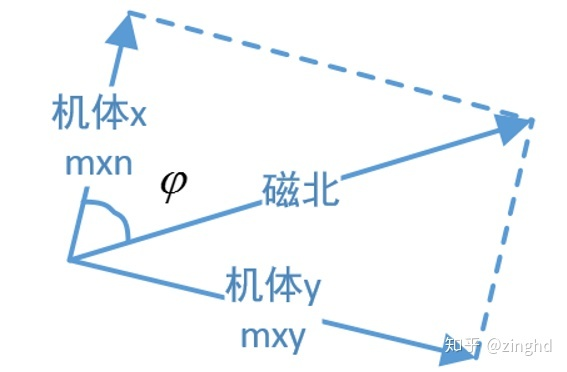
磁力計的三軸合向量會指向地磁北極,利用這一特性,可以從磁力計的輸出獲得與地磁北極的偏轉角。利用這一點,可以計算出相對于起始位置的角
具體的計算公式可以看這篇博客
從加速度計算的姿態彌補
從加速度計可以計算出roll角和pitch角,因此,可以將這個結果和角速度的積分結果結合起來,得到一個更好的估計姿態。不過要注意的是,從加速度計算的姿態彌補有兩個局限:
加速度計只能計算出Roll角和Pitch角,因此yaw角無法得到互補信息
當車輛處于較大的加速度運動狀態時,三軸加速度的合向量跟重力加速度會有偏差,因此互補結果應該根據這個偏差的大小做改變。
互補濾波器
互補濾波器使用角速度的積分結果和加速度與磁力計的計算結果進行插值,得到更好的結果 ? 其中,是對角速度積分得出的姿態(用四元素表達);是使用加速度計和磁力計計算出的姿態。
互補卡爾曼濾波器
互補卡爾曼濾波器將姿態角的誤差、角速度的誤差當作狀態向量;并利用其余傳感器如加速度計和磁力計計算出的姿態角與估計的姿態角之間的差作為測量量。通過以下步驟得到系統的姿態角:
卡爾曼濾波器輸出姿態角的誤差和角速度的誤差
將當前時刻角速度的輸出加上角速度的誤差,并利用積分公式算出姿態角
將步驟2算出的姿態角加上步驟1輸出的姿態角誤差
狀態向量和測量向量
狀態向量 ? 其中是系統的角;是三軸角速度。 測量向量 ? 其中,是使用加速度計和磁力計計算出的系統角
狀態方程
我們可以推導出姿態角對于時間的導數,通常這個導數是姿態角和角速度的函數,即 ? 從公式(4-1)的推導過程,以及泰勒展開,我們可以得到的遞推公式 ? 我們直接假設角速度的誤差是一個常量誤差,即 ? 則我們可以將上面兩式寫成矩陣形式 ?
測量方程
預測&&更新過程
有了上面狀態方程和測量方程的推導,剩下的就是按照公式(4-3)到公式(4-10)的過程代入。這里唯一不同的就是卡爾曼濾波輸出的向量是角速度的誤差和姿態的誤差。在計算姿態的時候先將角速度的誤差應用到角速度計的數據,對角度積分,將角度的誤差應用到角度積分結果,得到最終的角度輸出。整個框架如下圖
9后話
卡爾曼濾波是一個很古老的算法,但同時又是被廣泛應用的算法。即使在今天姿態解算中很多用了因子圖,但是對IMU的預積分依舊要使用卡爾曼濾波。但是卡爾曼濾波算法只是一個工具,不同的系統建模方式會產生不同形式的卡爾曼濾波器,這也導致了初學者不知道從哪里入手。
在查資料的過程中發現,卡爾曼濾波的一些變種如Error-State Kalman Filter和Complimentary Kalman Filter其實并不是嚴格定義的。
筆者對卡爾曼濾波并沒有很豐富的應用經驗,本身也不是專門做運動控制和姿態解算的。本文的敘述在追求通俗易懂之外盡力保證公式和符號定義的準確。但無法保證沒有錯誤。
對于卡爾曼濾波器中各個變量的初始值設置是門學問,論文中都會有獨立的章節講述初始值如何設置。這方面可能得結合實際應用和效果得出最優的方案。
10Reference
[1] Roll and Pitch Angles From Accelerometer Sensors [2] 四元數、歐拉角、旋轉矩陣轉換 [3] 四元素乘積求導 [4] 一種基于互補卡爾曼濾波算法計算融合姿態角度的方法 [5] Inertial head-tracker sensor fusion by a complementary separate-bias Kalman filter [6] Extended Kalman Filter vs. Error State Kalman Filter for Aircraft Attitude Estimation [7] Kalman Filter的原始論文 [8] 卡爾曼濾波基礎知識及公式推導 [9] AHRS: Attitude and Heading Reference Systems
編輯:黃飛
?
 電子發燒友App
電子發燒友App






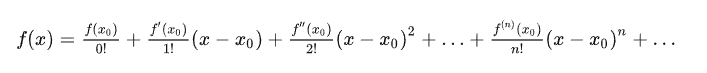
























評論