01 故事起源

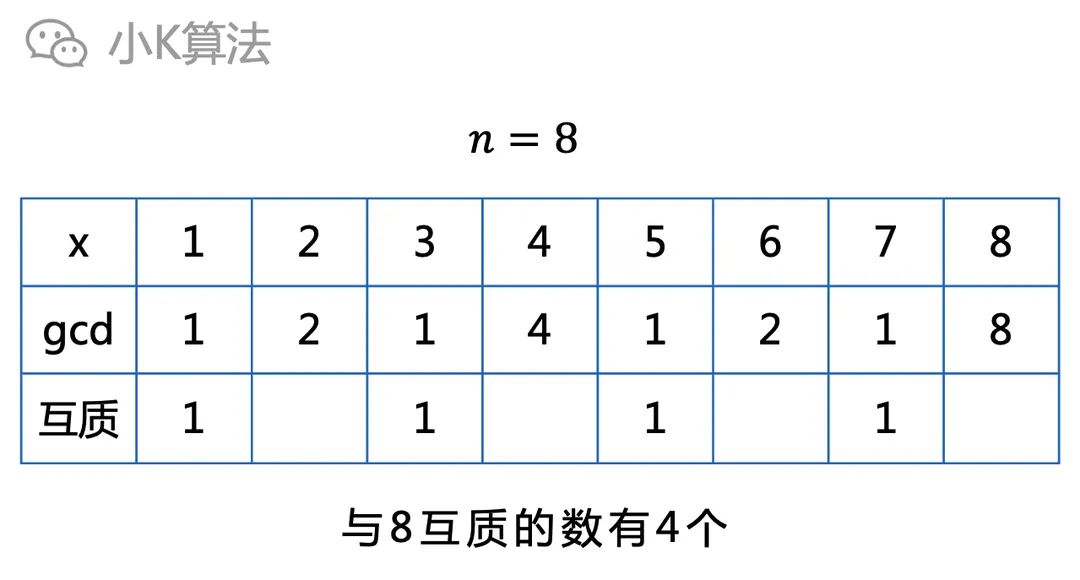
一個數n，在小于等于n的正整數[1,n]中，與n互素的數有多少個呢？

(注：x與n互素，說明x與n的最大公約數為1)

02 分析

最直觀的方法當然就是直接枚舉所有小于n的數，再通過求最大公約數判斷即可。

但當n很大的時候，這個方法就不優了。可能有同學已經發現了，這個不就是歐拉函數的定義嗎，所以今天我們從數學上來分析如何快速求解。

03 歐拉函數

歐拉函數定義如下：

歐拉函數具有幾個優秀的性質，先介紹幾個常用的數學符號，便于描述。

3.1 性質1

當n為素數時，很明顯phi(n)=n-1，因為所有小于n的數都與n互素。

當n為某個素數p的冪次時，即n=p^k，則與n不互素的一定為p的倍數。 [1,n]中p的倍數一共有p^(k-1)個，所以互素的即為總數減去不互素的個數。

3. 性質2

歐拉函數是一個積性函數，當整數m,n互素時，phi(mn)=phi(m)*phi(n)。

這個性質的證明需要用到同余和集合相關的定理，有點復雜，以后寫同余相關的知識再專門分享如何證明，現在就先記住這個性質就行了。

04 計算

有了這2個性質就可以推導出歐拉乘積公式。

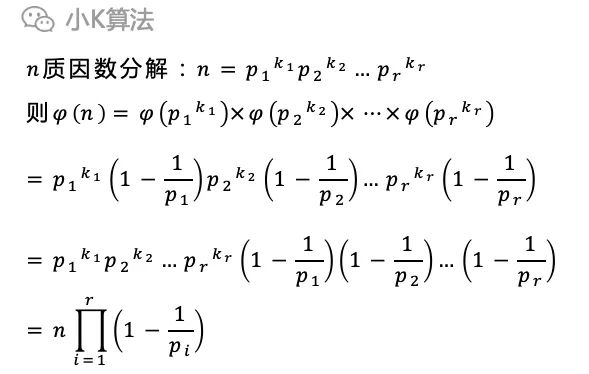
接下來就只需要考慮如何對n進行質因素分解。 最簡單的方式可以直接枚舉，先找到最小的質因子p1，然后除去所有p1因子，再對剩余的數繼續分解。

05 代碼實現