1. 論文信息
標題:Long-Tail Learning via Logit Adjustment
作者:Aditya Krishna Menon, Sadeep Jayasumana, Ankit Singh Rawat, Himanshu Jain, Andreas Veit, Sanjiv Kumar (Google Research)
原文鏈接:https://arxiv.org/abs/2007.07314
代碼鏈接:https://github.com/google-research/google-research/tree/master/logit_adjustment
2. 介紹
在傳統的分類和識別任務中,訓練數據的分布往往都受到了人工的均衡,即不同類別的樣本數量無明顯差異,如最有影響力的ImageNet,每種類別的樣本數量就保持在1300張左右。
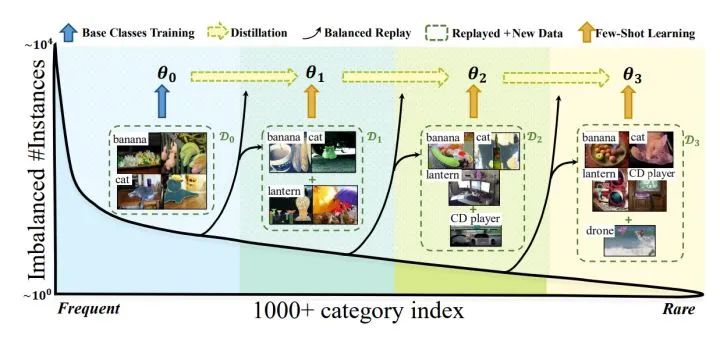
在實際的視覺相關任務中,數據都存在如上圖所示的長尾分布,少量類別占據了絕大多少樣本,如圖中Head部分,大量的類別僅有少量的樣本,如圖中Tail部分。解決長尾問題的方案一般分為4種:
重采樣 (Re-sampling):采樣過程中采樣不同的策略,如對tail中的類別樣本進行過采樣,或者對head類別樣本進行欠采樣。
重加權 (Re-weighting):在訓練過程中給與每種樣本不同的權重,對tail類別loss設置更大的權重,這樣有限樣本數量。
新的學習策略 (Learning strategy):有專門為解決少樣本問題涉及的學習方法可以借鑒,如:meta-learning、transfer learning。另外,還可以調整訓練策略,將訓練過程分為兩步:第一步不區分head樣本和tail樣本,對模型正常訓練;第二步,設置小的學習率,對第一步的模型使用各種樣本平衡的策略進行finetune。
其實就筆者喜歡的風格而言,我對重加權這一方向的工作更為喜歡,因為通過各種統計學上的結論,來設計很好的loss改進來解決長尾/不均衡分布問題,我喜歡這類研究的原因是,他們(大部分)實現簡單,往往只需幾行代碼修改下loss,就可以取得非常有競爭力的結果,因為簡單所以很容易運用到一些復雜的任務中。
而從“奧卡姆剃刀”來看,我覺得各種遷移模型的理念雖然非常好,從頭部常見類中學習通用知識,然后遷移到尾部少樣本類別中,但是往往會需要設計復雜的模塊,有增加參數實現過擬合的嫌疑,我認為這其實是把簡單問題復雜化。我覺得從統計方面來設計更加優美,因此本文來介紹一篇我非常喜歡的從統計角度出發的工作。這篇論文來自Google Research,他們提供了一種logit的調整方法來應對長尾分布的問題。由于研究風格更偏向 machine learning, 所以論文風格更偏向統計類。
本文首先總結了對于logit的調整方法:
聚焦于測試階段:對學習完的logit輸出進行處理(post-hoc normalization),根據一些先驗假設進行調整。
聚焦于訓練階段:在學習中調整loss函數,相對平衡數據集來說,調整優化的方向。
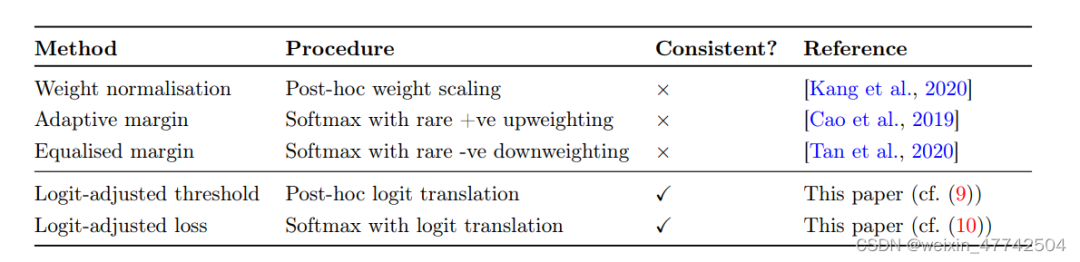
如上圖,這兩種方法都有許多較為優秀的工作,但是文中描述了這兩種方法的幾種限制:
weight normalization非常依賴于weight的模長會因為class的data數量稀少而變小,然而這種假設非常依賴于優化器的選擇
直接修改loss進行重加權,也會影響模型的表征學習,從而導致優化過程不穩定,同時模型可能對尾部類過擬合,傷害了模型表征學習能力。
論文的motivation就是克服這些缺點,讓不同類(head and tail classed)之間的logit能有一個相對較大的margin,設以一個consistent的loss,來讓模型的性能更好。
3. 問題設定和過往方法回顧
3.1 Problem Settings
論文先從統計學的角度定義了一下這個problem settings,其實就是訓練一個映射,讓這個scorer的誤分類損失最小:
但是類別不平衡的學習的setting導致P(y)分布是存在高度地skewed,使得許多尾部類別標簽出現的概率很低。在這里,錯誤分類的比例就不是一個合適的metric: 因為模型似乎把所有的尾部類別都分類成頭部類別也更夠取得比較好的效果。所為了解決這個問題,一個自然的選擇是平衡誤差,平均每個類的錯誤率,從而讓測試計算出的metric不是有偏的。
論文總結出了一個比較general的loss形式:
這里 是類別 yy 的權重;是另一個超參, 用來控制 margin 的大小。
3.2Post-hoc weight normalization
由于頭部類別多,容易過擬合,自然會對頭部類別overconfidence,所以我們需要通過一定的映射來調整logit。具體到調整的策略,自然是讓大類置信度低一點,小類置信度高一點。
for , where and . Intuitively, either choice of upweights the contribution of rare labels through weight normalisation. The choice is motivated by the observations that tends to correlate with . Further to the above, one may enforce during training.
這里引用了一些其他做long-tail learning的論文,可以參考以便更好地對這一塊進行理解。
3.3 Loss modification
至于對于loss的修改,就是很直接了在前面加一個權重,對于的取值,自然就是各個工作重點關注和改進的地方。
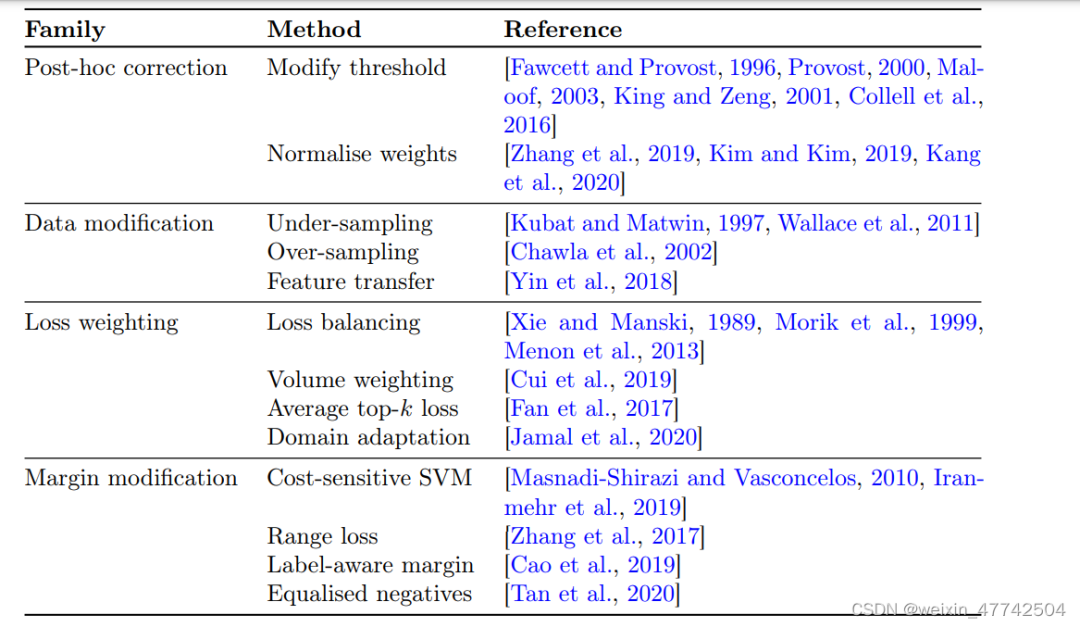
論文給予原有的各種方法各種比較全面的總結。
4. 方法
首先進行Post-hoc logit adjustment:
其實等號左邊就是一個根據類別的樣本數進行re-weighting。但是為了在exp的線性變換加上temperature時候不影響排序問題,所以把等號右邊變成上式,通過這種方式放縮不會導致原本的排序出現問題。從而使得重加權仍能夠給尾部類更高的權重。
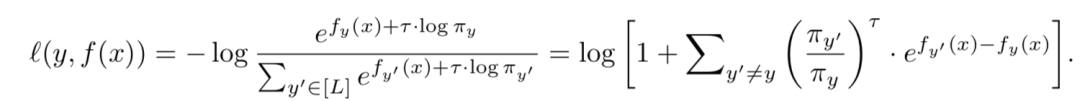
把loss改寫成易于理解的方式就如下:
下面這個更為直接的loss被成為為pairwise margin loss,它可以把 y 與 y' 之間的margin拉大。
然后就是實現結合:
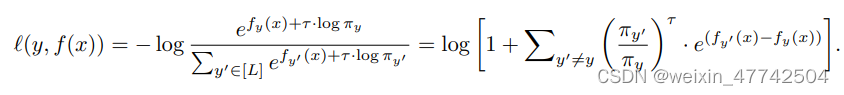
通過一些特殊的取值和另外的trick,可以實現兩者的結合。
5. 實驗結果
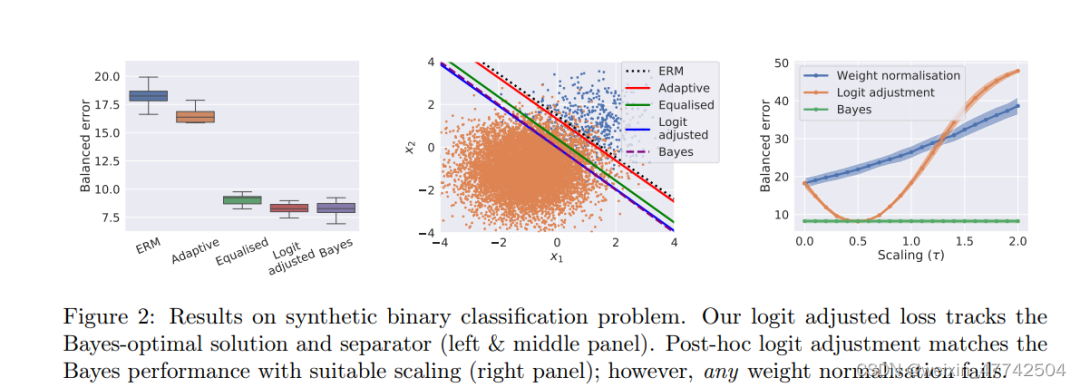
這張圖非常有意思,可以看出兩個設計理念非常有效果。
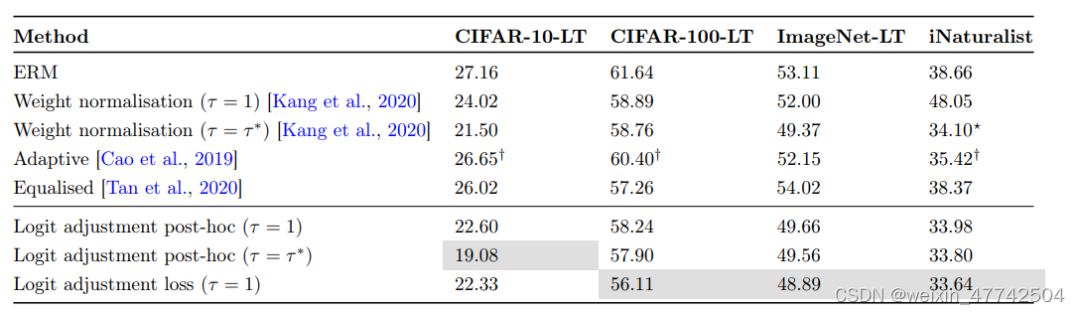
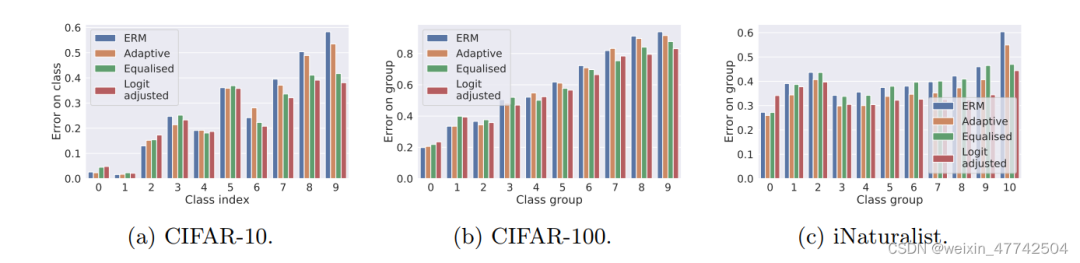
可以發現該方法在頭部類和尾部類的性能都有所提升。
6. 結論
摘要:這篇寫得很好的論文重新審視了logit調整的想法,以解決長尾問題。本文首先建立了一個統計框架,并以此為基礎提出了兩種有效實現對數平差的方法。他們通過在合成和自然長尾數據集上使用幾個相關基線對其進行測試,進一步證明了這種方法的潛力。
審核編輯 :李倩
-
線性
+關注
關注
0文章
199瀏覽量
25180 -
模型
+關注
關注
1文章
3297瀏覽量
49054 -
數據集
+關注
關注
4文章
1209瀏覽量
24789
發布評論請先 登錄
相關推薦
什么是機器學習?通過機器學習方法能解決哪些問題?

tlv320aic3104通過調整增益來控制聲音大小,調整一下就出現一聲“嘣“,如何解決?
如何調整TAS5729的BQ參數?
直流電機通過調整什么改變轉速
Linux操作系統運行參數自動調整技術
示波器萬用表功能調整方法
BP神經網絡的學習機制
深度學習模型訓練過程詳解
調速電機的速度調整范圍有哪些
淺析 KV 存儲之長尾時延問題,探尋行業更優解決方案!
機器學習8大調參技巧





 通過Logit調整的長尾學習
通過Logit調整的長尾學習










評論