1、疲勞強度評估的基本原理
首先,我們需要簡要地介紹一下疲勞強度的基本原理。在1830年,人們已經認識到一個相對于一般機械強度,較低往復式的應力同樣可以造成金屬的斷裂。隨后,標稱應力法(S-N curve)應運而生。這種方法主要是為了理解動態應力與出現金屬斷裂的時間的關系。一個典型對于金屬的S-N曲線如下圖所示:
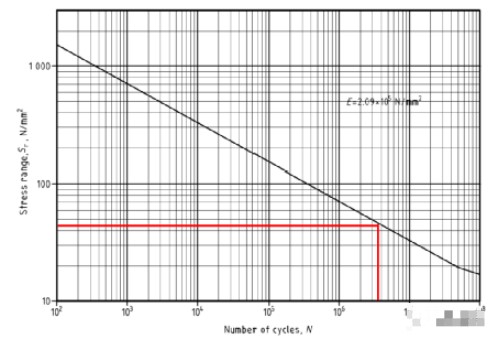
對于S-N曲線,它的橫坐標是金屬元件加載周期性往復力的次數,縱坐標是相應的極限疲勞波峰-波峰應力范圍(peak-to-peak range)。對于特定的往復力次數,當此元件的最大疲勞應力范圍大于S-N上所示的極限應力的數值時,這個元件就有極高的風險出現疲勞失效。


對于管道的振動問題,它往往和管道的固有頻率有關。可以看到,管道的固有頻率往往都是在100Hz以上。也就是說,機械振動所造成的位移都是相對較小的。因此,振動所造成的動態應變往往還是在材料的彈性區間以內。所以,高周疲勞還是通常比較普適的。因此,在接下來的文章中,我們主要討論如何使用S-N曲線來判斷管道的疲勞失效。
除了上述所述的動態應力對于材料疲勞特性的影響外,另一個重要的因素是管道內的壓力所造成的靜態應力(mean stress)。在1899年時,Goodman做了一系列的實驗,最終擬合出了一條直線。這條直線也被稱為Goodman曲線(如下圖所示)。
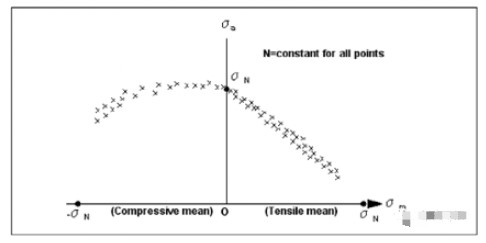
從這條Goodman曲線中,我們可以看到,隨著靜態應力的增加,疲勞應力極限會相應降低。根據這條Goodman曲線,我們可以使用下面這個式子判斷金屬元件是否會疲勞失效:

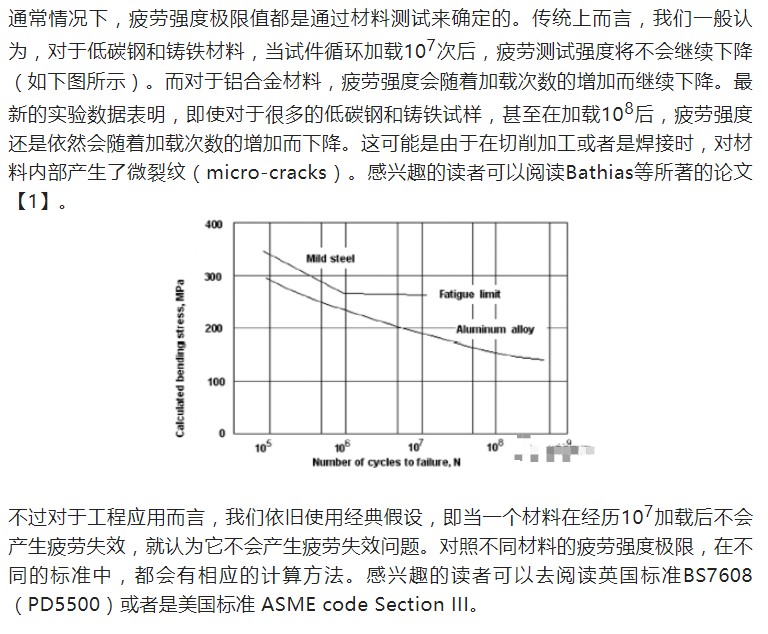
2、常見金屬的疲勞S-N曲線
3、管道的疲勞分析
對于一個典型的管道疲勞分析,最簡單的方式就是使用應變片來直接測量靜態與動態應力。但在實際工程上,這種方法還是存在一定的缺陷,下面讓我們看一個實際的管道案例。下圖顯示了一臺工程機械內的管道系統。從下圖中,我們可以看到這根管道是由不同的次級管道焊接而成的。
對于疲勞失效,它往往更容易出現在焊接點附近,主要原因是:在焊接過程中,焊接點周邊的金屬將承受更高的溫度,這些高溫會在金屬內部造成許多微裂紋(micro-cracks),從而造成更低的疲勞強度。遺憾的是,這些微裂紋的分布在同一焊接平面內并不是均勻的。也就是說,較低的疲勞強度可能出現在管道焊接截面上的任意位置。
回到我們所說的應變片應力測試的問題,可以看到,在焊接管道的截面上,焊接的質量也不一定完全一致。由于這個原因,在不同位置所能測到的應力集中系數(stress concentration factor)也會有所不同。在這種情況下,就很難判斷在哪個位置需要貼應變片來測試應力。
其次,我們可以看到,由于應力集中的原因,在接近焊趾的金屬位置,它所受到的應力將遠遠高于遠離焊趾的位置,并且,應力測試距離與最大應力的關系是一條類似于雙曲線的關系。
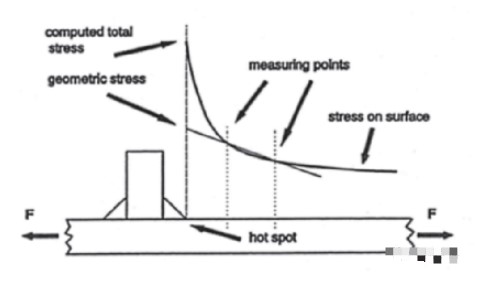
對于一般的應變片而言,它有一定的尺寸。我們所測到的應力值是在應變片所粘貼的面積上的平均應力。也就是說,在焊趾附近貼上的一個應變片所測試到的平均應力很有可能比實際上的最大應力值(hot-spot stress)更低,從而導致我們低估了這個金屬元件的最大動態應力。
還有一個更重要的原因是難以決定應變片粘貼的位置。由于工程上使用的管道普遍是三維的,我們很難預測最大的振動出現在哪個方向上,所以最大應力在管道截面上出現的位置也往往難以確定。如果我們只進行應變測試,需要粘貼許多應變片。而應變片測試往往相對比較復雜,特別是應變片的電氣絕緣較難實現。所以,通常對于應變片會獲得更高的背景噪聲。更麻煩的是,對于高頻振動,結構所受的應變往往相對較小,一般應變片的信噪比并不足以獲得可靠的應力數值,所以,應變測試一般不是一個很容易且方便快速的選擇。
相對而言,使用加速度計進行的振動測試往往十分便捷可靠迅速。除此之外,我們可以看到,在很多狀況下,振動的數值直接與機械應力呈正比。所以往往可以使用管道最大的振動值來進行疲勞失效的篩查方法。在下一小節,我們將介紹一種基于振動速度的簡化方法來判斷管道疲勞失效的可能性。
4、基于振動管道疲勞失效篩選方法
為了建立管道的最大速度與最大動應力(dynamic stress)的關系,我們需要判斷管道的振型(mode shape)。基于振型,可以推導出管道彎曲的曲率(curvature),通過這個曲率我們可以推導在邊界條件處(boundary condition)的最大應力。不過這個過程需要相對復雜的數學建模,一般不利于工程應用。在下一篇文章中,我們將會詳細介紹。在這一小節,我們僅僅介紹一種工程上常用的方法,這個方法是基于德國國家標準VDI3842 。
下圖是在VDI3842第7.2.3節提供的一種基于最大RMS振動速度的判斷準則。
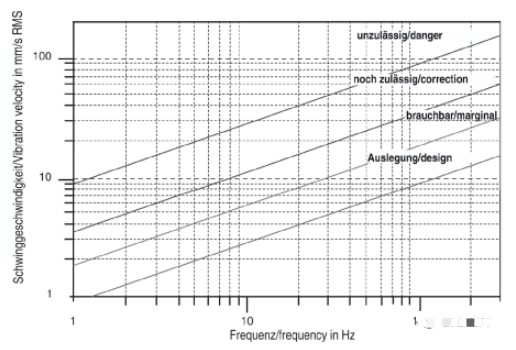
值得注意的是,這個標準中的曲線只能適用于初步的分析。原因有二:(1)這個圖僅僅適用于300Hz以下的振動,對于很多應用而言,振動頻率遠遠高于300Hz,它將不再適用;(2)這個振動的標準是基于石化行業經驗而來的,也就是說,它只適用于管徑和管道支撐間隔,類似于石化行業的管道,對于很多應用它并不適用。所以,我們需要使用其他的方法來將管道振動轉化為最大的應力。由于這個原因,VDI標準也提供了另外一種方法來完成這個轉換。在這個方法中,確定最大應力的近似公式是:

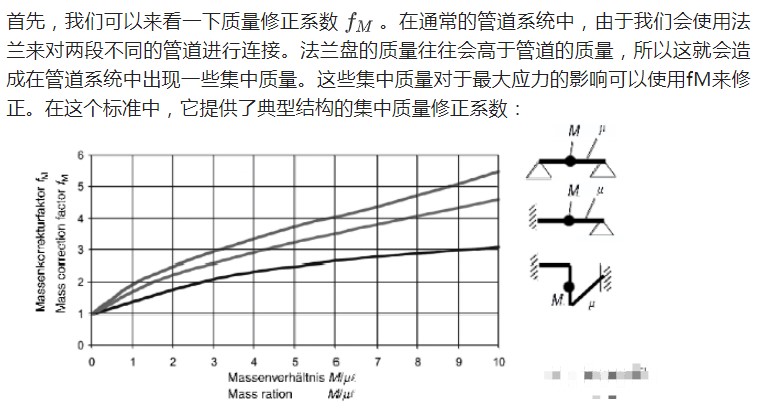
其次,我們來討論下對于管道結構的修正系數;例如,如果管道上存在一些常見的部件時,它對于管道彎曲的曲率影響補償系數。
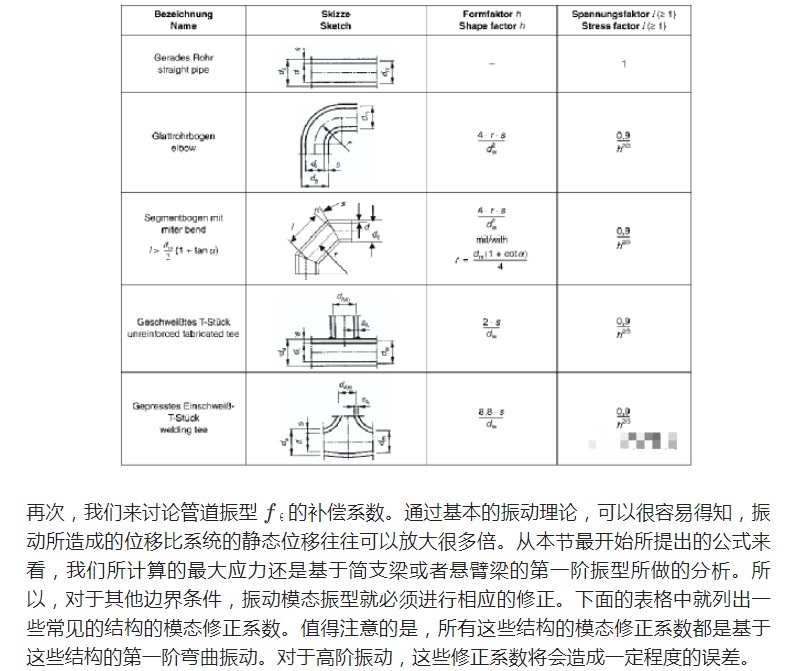
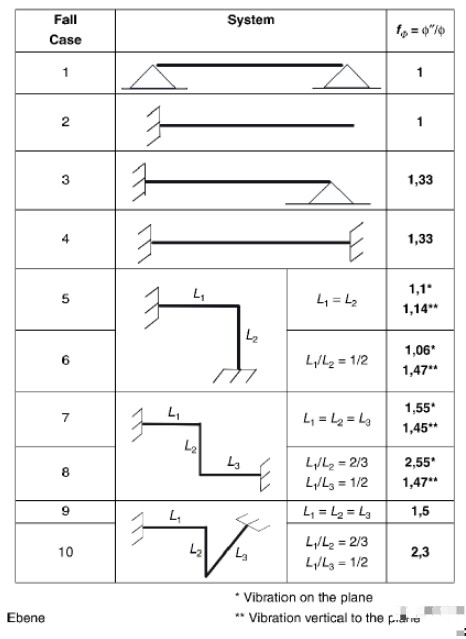
可以看到,以上這些修正都是基于一系列很有限的結構。比如說,對于集中質量的修正,它只提供了三種不同邊界條件,并且,集中質量的位置對于模態也會有影響,這些影響并沒有考慮到這個修正系數中。同樣地,對于模態振型的修正,也存在同樣的問題。對于實際的管道系統,它遠遠比我們看到的例子復雜,如果僅僅使用上表中的結構,只能尋找最為類似的結構。在這種情況下,會引入更多的誤差,最終造成對于管道結構的過度設計。由于這些問題,我們需要引入更復雜的方法(Rayleigh-Ritz法或者有限元的方法)來進行設計。在下一篇文章中,我們首先會用一些簡單的結構來驗證這個VDI的方法,之后會簡要介紹Rayleigh-Ritz法來求解結構的振型,隨后,這些振型將用來求解最大應力。最后,我們將用一個實際的例子來解釋如何使用這種方法來評估管道結構的疲勞。
審核編輯:劉清
-
應變片
+關注
關注
1文章
46瀏覽量
11419 -
信噪比
+關注
關注
3文章
260瀏覽量
28688 -
加速度計
+關注
關注
6文章
704瀏覽量
45981
發布評論請先 登錄
相關推薦
什么是失效分析?失效分析原理是什么?
交流電誘發銅互聯體的熱疲勞失效行為及微觀分析
油氣管道失效分析與完整性管理
國內外失效評定曲線(FAC)的發展以及現狀
運用焊接結構的S-N曲線獲取焊縫裂紋擴展規律的特征參數
單個沖擊對不銹鋼管道焊接頭低周疲勞壽命的影響
航空液壓管路疲勞壽命數值預估
550 kV斷路器用密封桿疲勞分析及試驗研究
磁感線是閉合曲線嗎_磁感線判斷方法




 如何使用S-N曲線來判斷管道的疲勞失效
如何使用S-N曲線來判斷管道的疲勞失效










評論