頻率基準需要振蕩器。所有時鐘都用于(微)處理器,但所有計時電路也需要一個時鐘 。以晶體作為基準,可以獲得了最高的精度;無需大量的努力,0.1%的精度就能輕易獲得。這就是為什么我們從晶體振蕩器開始這一章。結果表明,只需要一個晶體管就可以構造一個晶體振蕩器。
在設計這個振蕩器之前,我們必須回顧一下振蕩的條件,之后我們來看看這種晶體的電氣模型是什么;它現在可以用來構造一個具有最小功耗的單晶體管振蕩器。MOST晶體管和雙極晶體管都可以用來實現這種振蕩器。最后,振蕩的原理可以擴展到構造其他類型的振蕩器,如壓控振蕩器 (ωoltage Controlled Oscillator, ωCO) 等。
振蕩器原理
振蕩器是一種反饋放大器,反饋的信號正是放大器維持振蕩所需要的,它的輸入現在為零。這被稱為巴克豪森標準 ( Barkhausen Criterion )。該放大器具有依賴于頻率的增益A(jω),此外反饋塊具有與頻率相關的衰減F(jω)。環路增益F(jω)A(jω)必須足夠大,以便反饋的信號vf完全等于ve,這是必需的。結果,環路增益在振幅上必須略大于單位增益,相位為零。
這意味著如果F(jω)是衰減器,則A(jω)必須是放大器;這也意味著如果A(jω)是電容性的,則F(jω)必須是電感性的。我們所見過的所有放大器都包含電容, 因此我們需要為Fjω) 找一個電感。顯然,這兩個條件是 A(jv) 和 F(jv) 的復數性質的結果, 復數總是成對的數字。
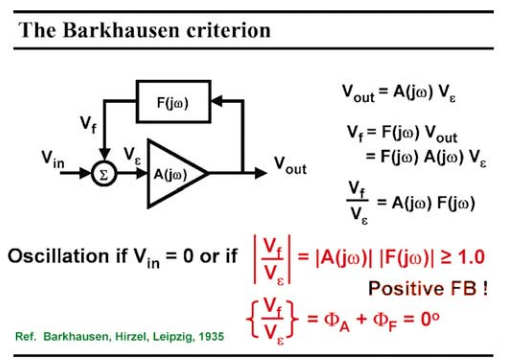
圖 1 巴哈豪森 ( Barkhausen ) 振蕩 (條件) 標準
另一種寫巴哈豪森標準的方法是通過分裂分析給出的。放大器現在由阻抗Zcircuit表示,反饋元件由諧振器阻抗表示。由于電路自身可以保持振蕩,因此不需要來自外部的電流;其總輸入導納量為零,阻抗的和也必須為零。巴克豪森標準現在可以用下圖中的兩個表達式來表示:現在使用的是實部和虛部,而不是幅度和相位,它們顯然是相關的 。我們之后會看到,第一個表達式決定了所需的最小增益,另一個表達式決定了它的實際振蕩頻率。
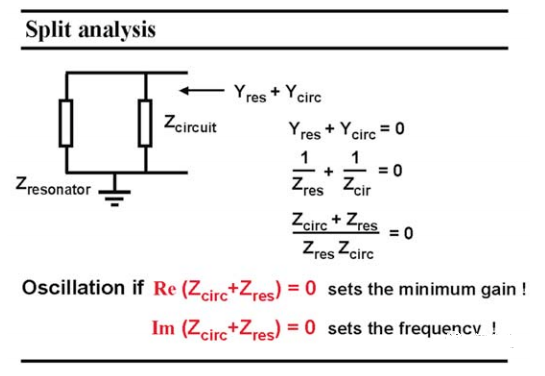
圖 2 拆分分析
晶體振蕩器
現在了解了振蕩的條件,讓我們找到電感來與電容放大器形成一個反饋環路,我們知道它們可以一起形成一個振蕩器。我們使用的第一個電感是嵌入在晶體中的。
晶體是由具有一定厚度d的壓阻材料板組成。壓阻材料允許機械能和電能的交換。例如石英、氧化鋅和一些氮化物。對其施加一個機械壓力,會產生一個電壓,反之亦然。這種能量交換在一個特定的頻率上特別有效,這個頻率稱為諧振頻率fs,其與石英的厚度成反比。通常會制作100kHz到40-50MHz的振蕩值,對于較高的值,石英變得太薄和脆弱。
在這個諧振頻率周圍,該晶體的電氣模型是一串聯的諧振LRC電路,其諧振頻率為fs。它受到串聯電阻 Rs 的阻尼,從而導致品質因數 Q 是有限的。下圖中給出了所有相關的表達。請注意,在諧振時,電感的阻抗等于電容的阻抗。實際上,在諧振時,串聯 RLC 電路本身就是 Rs, 電感Ls和電容Cs相互抵消。除了代表晶體機電運行的這個串聯 RLC 電路外,還必須添加一個平板電容 Cp。它是用于接觸晶體的兩塊板之間的電容,具有石英的介電常數(比空氣大 4.5 倍)。它還包括與封裝有關的電容。
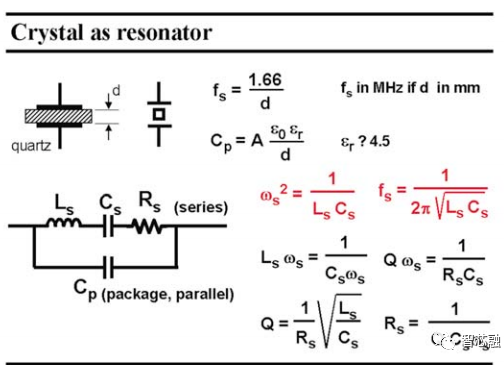
圖 3 晶體作為諧振器
例如,10.00MHz的晶體可以用約10mH的電感,串聯26fF的電容和 5Ω的阻尼電阻的串聯LRC建模,注意電感相當大,電容非常小。一個經驗法則說,它們大約是封裝電容Cp的1/200到1/250。板式或封裝式的電容總是在pF的數量級上,串聯電容Cs始終在fF范圍內。電阻非常小,因為質量系數Q很高,在105數量級左右!很明顯,封裝電容Cp與Ls也形成了一個并聯諧振電路。我們同時有一個串聯和一個并聯的諧振電路!然而,我們嘗試在串聯諧振頻率fs下制造一個振蕩器,因為這是內部晶體頻率,獨立于封裝或安裝。
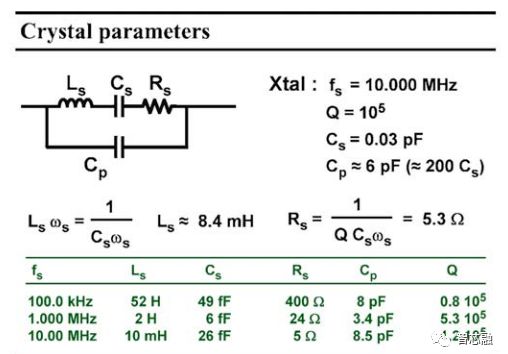
圖 4 晶體參數
為了回憶起串聯和并聯振意味著什么,兩者都繪制在下圖。兩者對諧振頻率fr具有相同的表達式, 然而阻抗與頻率的關系看起來非常不同:串聯諧振電路的諧振處有明顯的零,在諧振時,阻抗降低到電阻R, 晶體是純電阻的;對于低于fr的頻率,電容的阻抗增加,從而決定了電流,阻抗為電容性,相位為?90°。對于高于fr的頻率,阻抗變為感性,其相位為 90°。
一個并聯的諧振電路在諧振處有一個尖銳的峰值。在諧振時,阻抗受到電阻R的限制,晶體同樣是純電阻的。對于低于fr的頻率,電感的阻抗減小,從而決定了電流。阻抗為感應的,相位為90°。對于較高的頻率,阻抗變成電容性,其相位?為90°。這與串聯諧振電路正好相反。
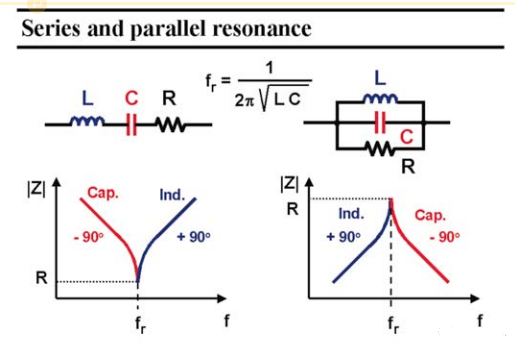
圖 5 并聯和串聯諧振器
現在讓我們回到晶體中,在下圖中繪制出它的阻抗與頻率。它用一個三階表達式清楚地描述,如下圖所示。一般來說,它顯示了封裝電容Cp的阻抗,它會隨著頻率的增加而減少。在諧振頻率附近,我們注意到零點和峰值非常接近。零點在前,代表諧振頻率為 fs 的串聯諧振,而峰值代表并聯諧振。現在我們把這個區域放大;
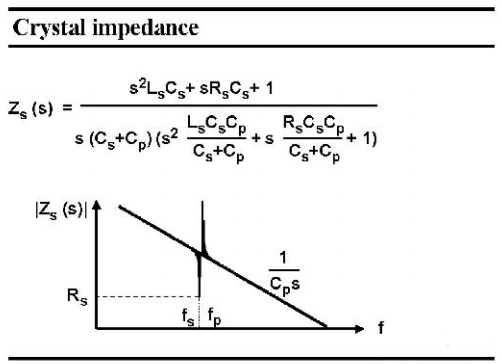
圖 6 晶體的阻抗
現在諧振頻率很容易區分,串聯諧振頻率fs是那個較小的。實際上已經計算出了給定晶體的值。下圖上面顯示了振幅,而底部的圖顯示了相位。如前所述,晶體在串聯諧振頻率 fs 的左側和并聯諧振頻率 fp 的右側充當電容。
然而,在兩個諧振頻率之間,晶體作為一個電感。由于質量系數很高,因此過渡幅度非常陡。該晶體現在作為從并聯諧振頻率fs到串聯諧振頻率fp的電感。我們使用這個電感和一個電容式放大器來制造一個振蕩器。我們希望這個振蕩器的工作在盡可能接近串聯諧振頻率fs,因為這是最接近晶體內部機電運行的頻率。此外,這也是最不依賴于封裝和安裝電容的頻率, 這些封裝和安裝電容難以預測。然而我們會看到,不可能在串聯諧振頻率fs下產生一個振蕩器,這將需要無限的電流!然而,我們將盡可能的接近,這取決于允許使用的電流。
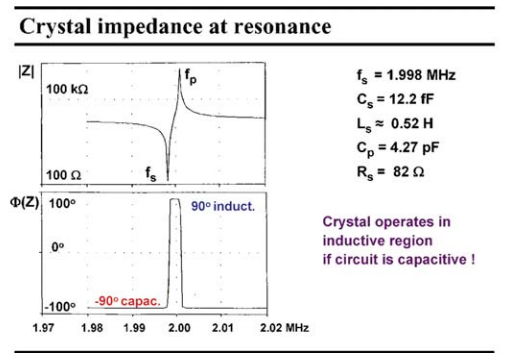
圖 7 晶體在諧振時的阻抗
下面給出了串聯諧振頻率fs和并聯諧振頻率fp的實際表達式;串聯的如下圖中所述,另一方面,并聯諧振頻率fp由兩個串聯電容確定,通過檢查模型可以清楚地看出。這個頻率總是比串聯的要大一些。如果我們發現Cp比Cs大了約200倍,那么 ωp2大約比 ωs2大0.5%。此外,ωp比 ωs大約0.25%。RLC串聯電路的阻抗現在可以在下圖中描述,在引入牽引因子 p 之后,我們將重寫這個阻抗。這個牽引因子p是無量綱參數,它說明了實際工作頻率距離串聯諧振頻率fs有多遠。引入這個因子p和頻率fs,給出了串聯RLC電路阻抗的另一個表達式。據認為這個阻抗是電阻Rs和一個電感串聯,這個電感越偏離串聯諧振,就越大。我們將用這個簡單模型來尋找振蕩器的振蕩條件。
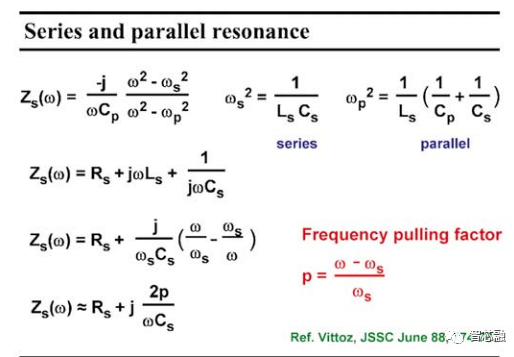
圖 8 并聯和串聯諧振
術語串聯或并聯諧振通常歸因于電路配置, 然而我們將會看到這是錯誤的!
串聯和并聯諧振只與振蕩器的工作點有關。對于零或非常小的牽引因子p,工作點接近fs。在這種情況下,我們顯然有一個串聯振蕩器;對于一個相當大的p,工作點接近fp,我們將其稱為并聯振蕩器,雖然Cs在確定振蕩頻率方面的重要性仍然是Cp的200倍。中間的點是串聯和并聯諧振之間的交叉值fm。由于在fp時,牽引因子p約為0.25%,因此中間點的牽引因子一定約為其的一半或0.125%。我們現在可以得出結論,牽引因子p必須小于0.1% 左右,才能有一個具有良好的穩定性和可預測性的振蕩器!
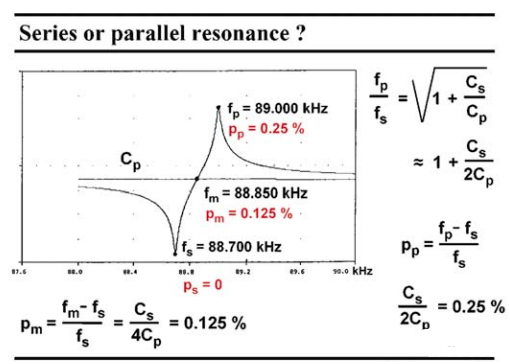
圖 9 并聯或串聯諧振?
-
振蕩器
+關注
關注
28文章
3847瀏覽量
139279 -
反饋放大器
+關注
關注
0文章
35瀏覽量
7874
發布評論請先 登錄
相關推薦
晶體振蕩器的選用
晶體振蕩器分類簡單易懂小知識
晶體與晶體振蕩器
晶體振蕩器的分類
晶體振蕩器的分類




 關于振蕩器和晶體振蕩器應用分析
關于振蕩器和晶體振蕩器應用分析










評論