我們知道,不論是buck,還是boost電路,總會有一些公式,用得最多的就是電感的感量計算,電流紋波,輸入電壓紋波大小,輸出電壓紋波大小等等。
這些公式,在我們設計的時候會去算一算,很多的DCDC的芯片手冊里面也會有這些公式。
就我自己而言,我是很討厭背公式的,相信大家也一樣。
所以最好的方式莫過于充分理解電路的工作原理,甚至于可以自己推導出這些公式。
我們如果理解了這些公式,那么就理解了Boost電路各個地方的電流,電壓是怎么樣的,遇到一些問題,就可以不用去看公式就能知道為什么會這樣。
比如電感感量增大,會怎么樣?
電容容量增大會怎么樣?
工作頻率的大小又有哪些影響呢?
所以,推導公式是為了擺脫公式。
另外,計算之后,我們會發現:
計算結果跟實測結果經常差的比較多?根本就不準?為什么呢?
這些問題,本文都會說一說。
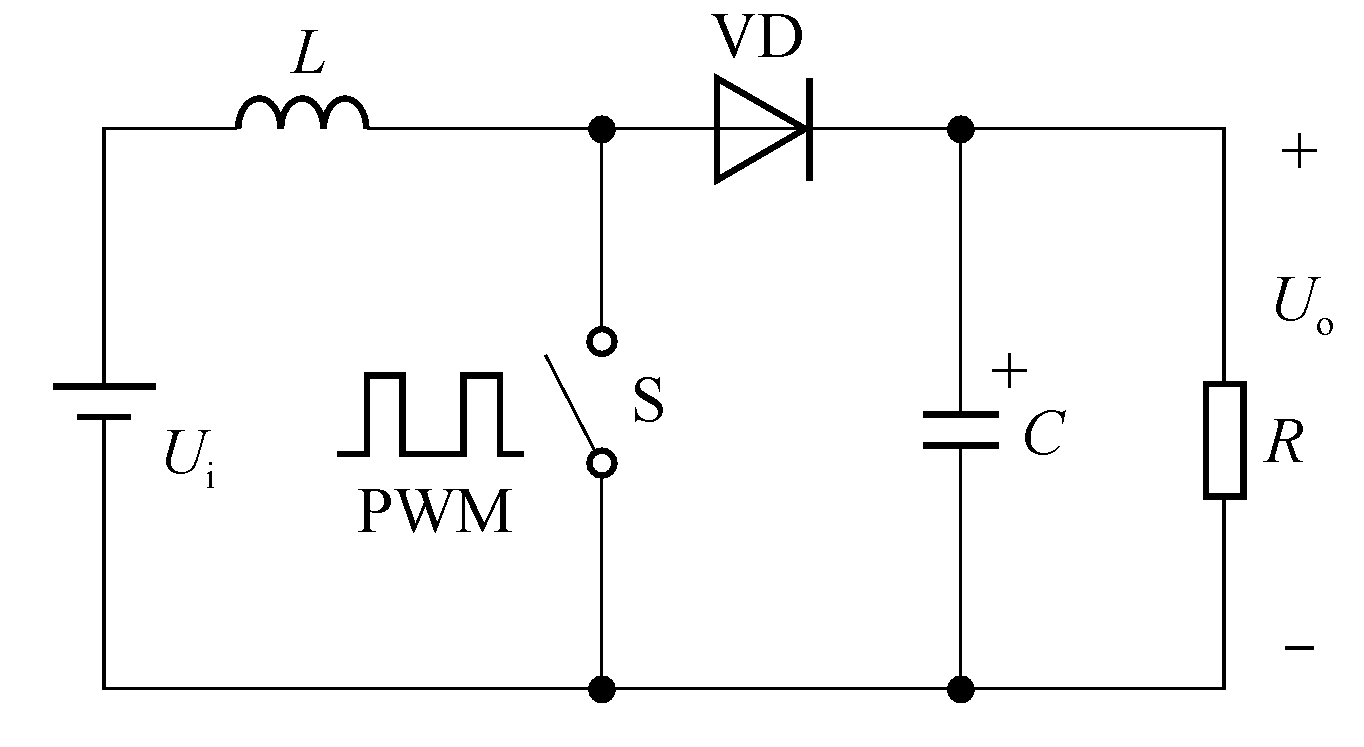
Boost的拓撲結構
我們先來看拓撲結構,一切信息都在這個里面。
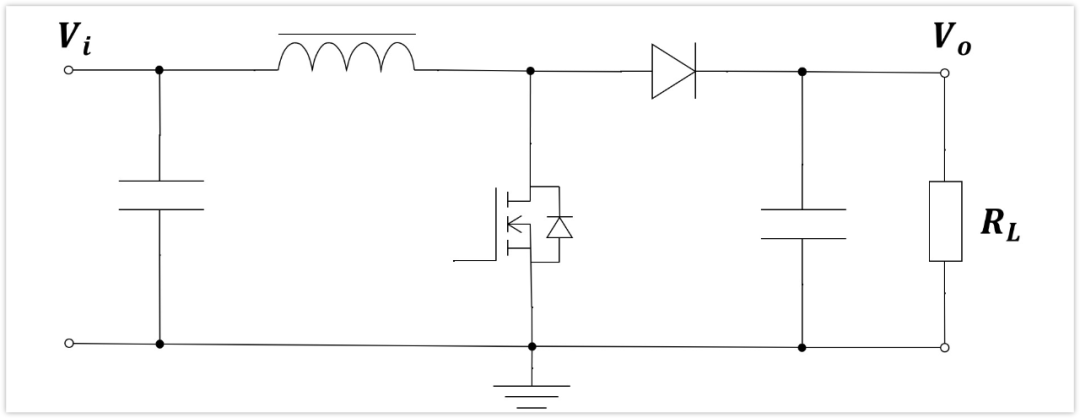
首先說下最基本的一個工作原理。
上圖中MOS管就是一個開關,只要這個速度夠快(開關頻率夠高),控制好導通與關斷時間(充放電時間),配合輸出濾波電容,就可以得到基本穩定的Vo了,也就是輸出電壓。
我們來簡單看一下過程。
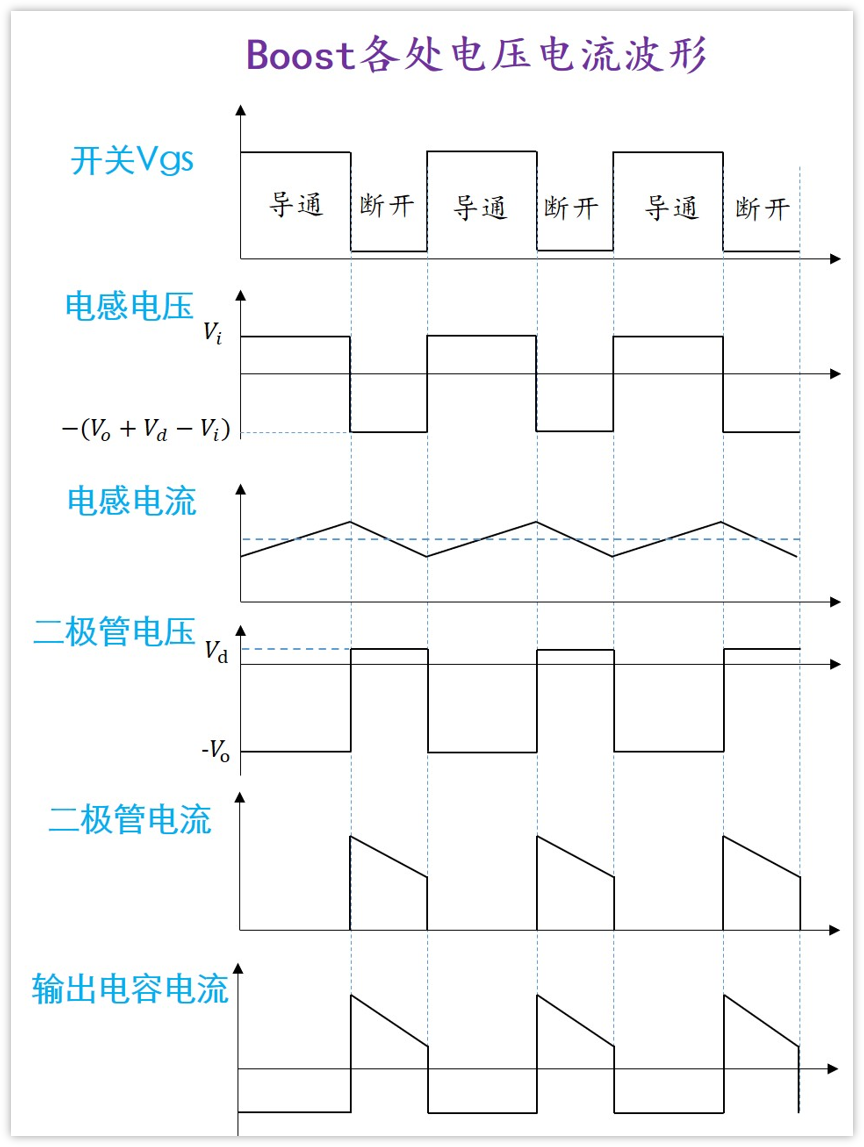
在開關導通的時候,電感L接地,二極管截止,Vi對電感L進行充電,電感兩端電壓是Vi。
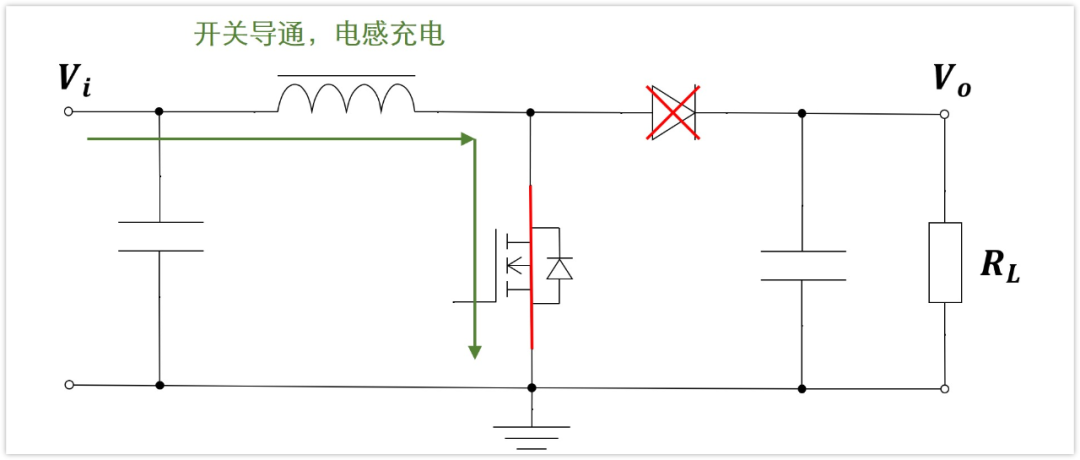
在開關變為不導通的時候,因為之前電感L已經被充電了,有電流流過,電流向右,電感兩端電流不能突變,所以會感應出電壓,讓右側的二極管導通。
輸出電壓Vo恒定,二極管導通壓降為Vd,所以電感右端電壓為Vo+Vd,電感左端電壓是電源輸入Vi。這是升壓boost電路, 所以Vo+Vd》Vi,電感此時放電,給負載供電,以及給輸出濾波電容充電。
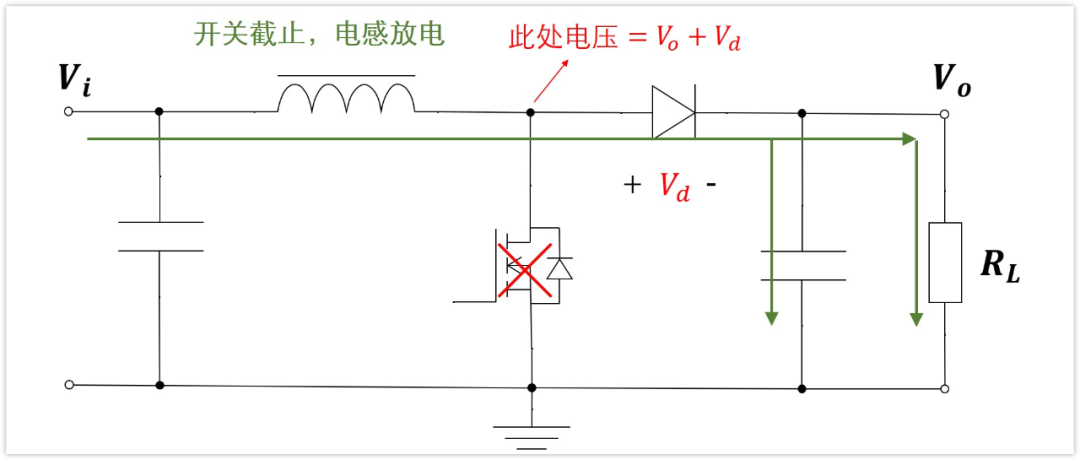
并且,此時電感的兩端電壓是右邊電壓Vo+Vd減去左邊電壓Vi,即:Vo+Vd-Vi
來個前菜加深理解
Boost電路是升壓電路,是直流轉直流,不考慮紋波電壓的話,Vi和Vo都是恒定的,Vo大于Vi。
在開關導通的時候
電感L一端是恒定電壓Vi,另外一端接地。這說明在開關導通的時候,電感L兩端的電壓是恒定不變的,就是Vi。
根據電感最最最最基本的公式:U=L*di/dt。
(雖然我不喜歡背公式,但是這個公式我覺得是電感最重要的了,我之前還專門講過,它可以推導出電感儲能公式等等。同樣,電容的最重要的公式:i=C*du/dt。)
好,電感兩端電壓U=Vi不變,電感量L也是常數,所以呢,di/dt=U/L=常數,這不就是說電流隨時間線性變化嗎?

如果我們規定電流流向負載的方向是正,根據電感此時電壓,是左邊大于右邊,所以電感的電流是線性增大的。
當開關斷開的時候
電感兩端的電壓U=Vo-Vi-Vd,也是恒定的,電流同樣隨時間線性變化。只不過電壓的方向是反的,右邊大于左邊,所以電感的電流是線性減小的。
開關導通,電感電流線性增大。
開關斷開,電感電流線性減小。
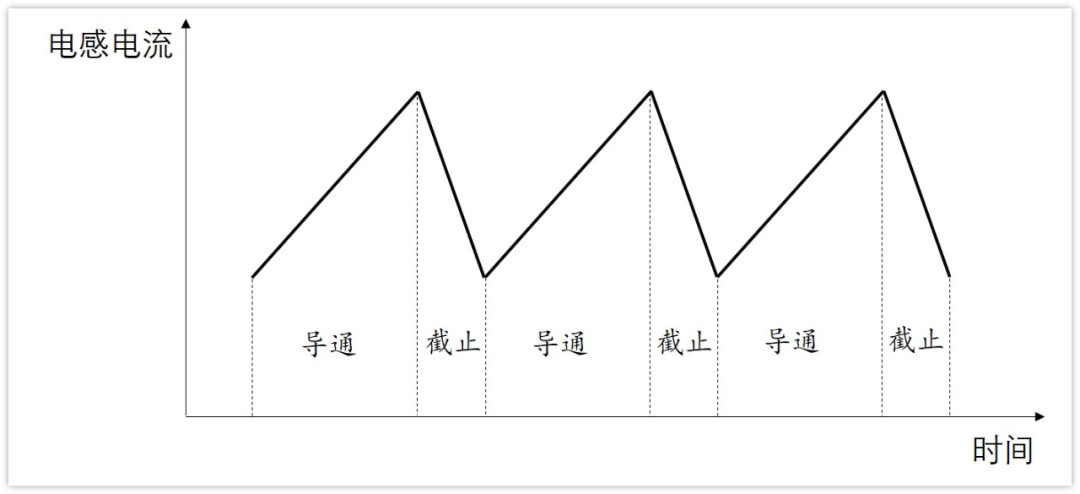
我第一次看到電感電流波形是這樣的時候,我就覺得好巧啊,怎么就一定是線性上升呢?不是曲線上升?
現在自然是知道了,當然,知道也好像沒什么卵用,那說點兒有用的。
我們在電感選型的時候,一定知道有個參數叫飽和電流吧。
我們會要求,電感的峰值電流不能超過電感的飽和電流。
為啥是峰值電流,不是有效值電流?
因為,我們一般認為電感的感量是不變的,但是實際情況是,電流大到一定程度的時候,電感量L會隨電流的增大而減小,所以會有電感飽和電流這一說。
并且,隨著電感電流的繼續增大,電感量下降速度加快。
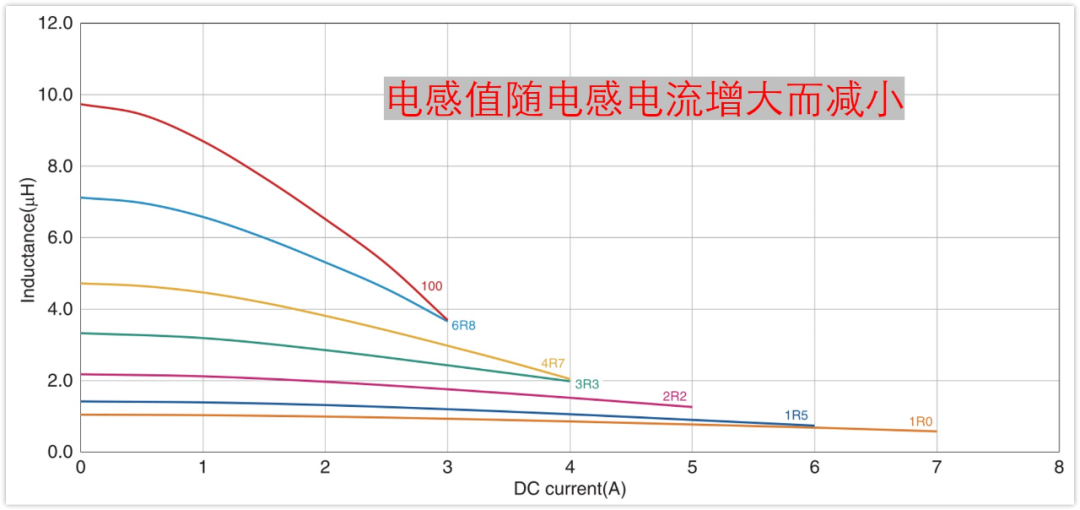
我們復習下電感這個曲線,很多電感手冊都有,電感的飽和電流是指電感感量下降了標稱值的30%(不同廠家這個值有差異)的時候的電流。
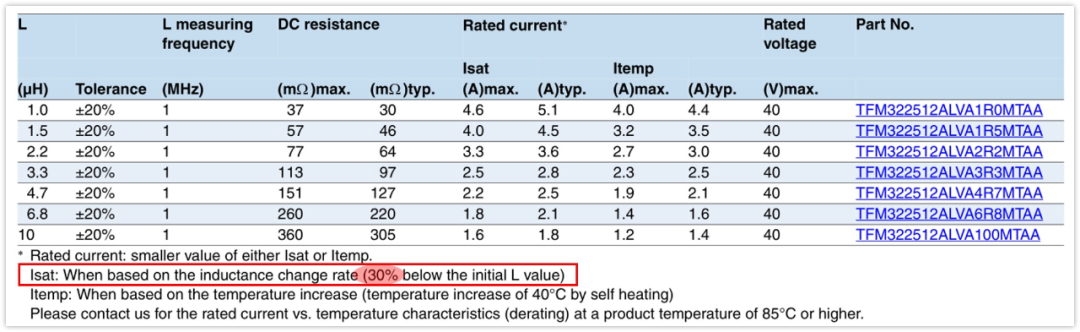
如果選型的電感飽和電流太小會怎么樣呢?
開關導通,電感電流增大,增大到飽和電流的時候,那么L會快速減小,意味著di/dt=U/L快速增大。
也就是說,di/dt變大了,即電感電流隨時間更快的增大。
電流更大了,那么進一步電感感量L更小了,di/dt更更更大了,電流又更更更大了。
如此,電流就突破天際了,這就悲劇了。
簡單畫個圖,感受一下。
好了,根據前面的分析,我們還是畫出幾個關鍵點處的電壓和電流波形吧,這應該是沒什么難度的,最難的應該屬于那個電感電流的波形了,我們也解釋過了。
開始推公式
我們推公式,自然是為了更好的選型,對吧。
目的為了計算出輸入電容,輸出電容,功率電感,都選擇多大的值。
為了更好的理解,我們把已知的條件都說一下。
首先是輸入電壓Vi,輸出電壓Vo,輸出電流Vo/R,咱總得知道自己想要什么吧,所以這些在設計之初都是已知的。
其次是開關頻率fs,這個在芯片選型之后就是確定的了。
再然后就是設計的目標,輸入紋波大小△Vi,輸出紋波大小△Vo。
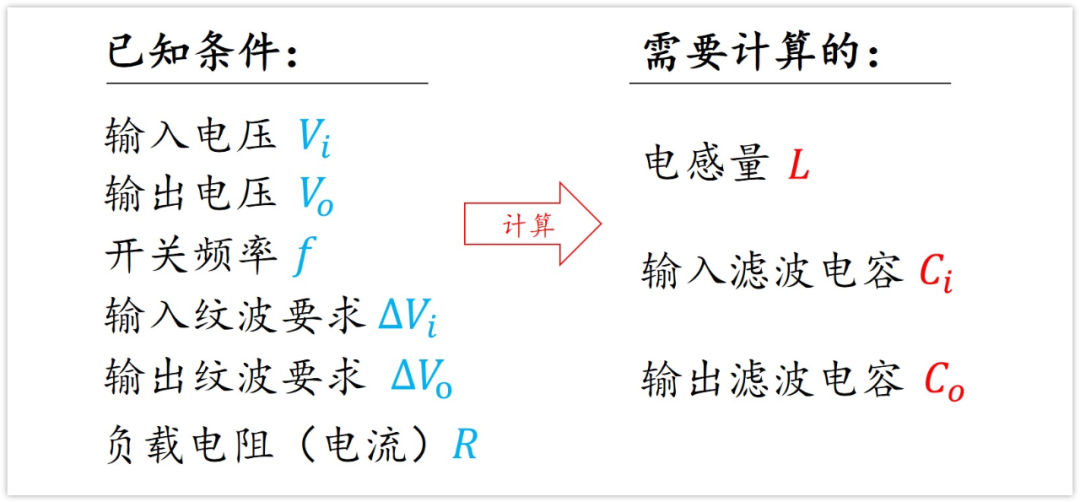
我們根據這些已知的量,就可以求得電感感量,輸入濾波電容大小,輸出濾波電容大小。
好,我重新把圖畫一下,如下:
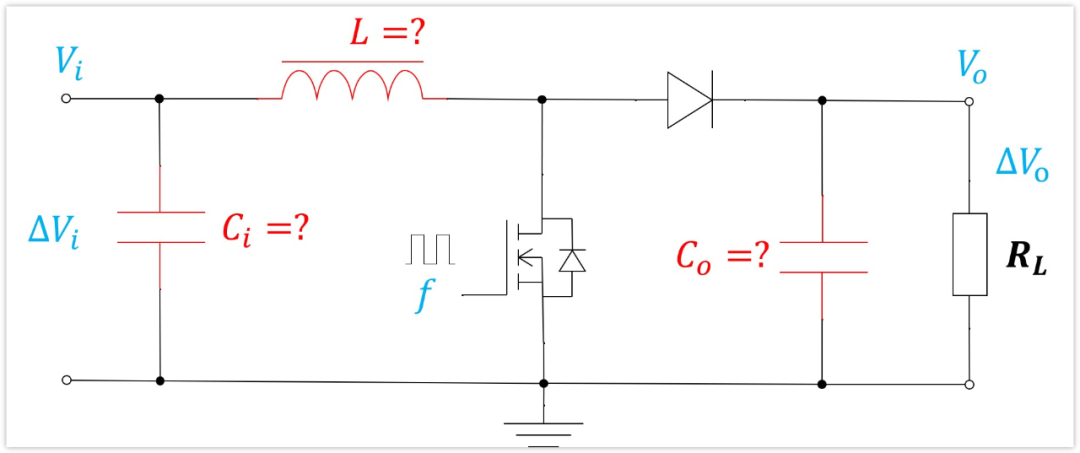
因為計算的基本原理其實就是電容和電感的充放電。所以,我們首先要求的就是開關導通的時間和斷開的時間,或者說是占空比。
這個也非常簡單,我們可以這么想。
在開關導通的時候,電感兩端電壓是Vi。
在開關斷開的時候,輸出端電壓為Vo,二極管導通,那么電感右側就是Vo+Vd,電感左側接的是電源輸入,為Vi,所以此時電感兩端電壓是Vo+Vd-Vi。
整個電路穩定之后,因為負載電流恒定,那么一個周期時間之內,在開關導通時電感電流增加的量,要等于開關截止時,電感電流減小的量,即電感充了多少電就要放多少電,不然負載的電流或者電壓就要發生變化。
即一個周期內,電感電流增大量等于減小量。
然后又因為U=Ldi/dt,di/dt=U/L,L不變,所以電感電流變化速度與電壓成正比。
簡單說就是,電感電流上升或下降的斜率與電壓成正比。
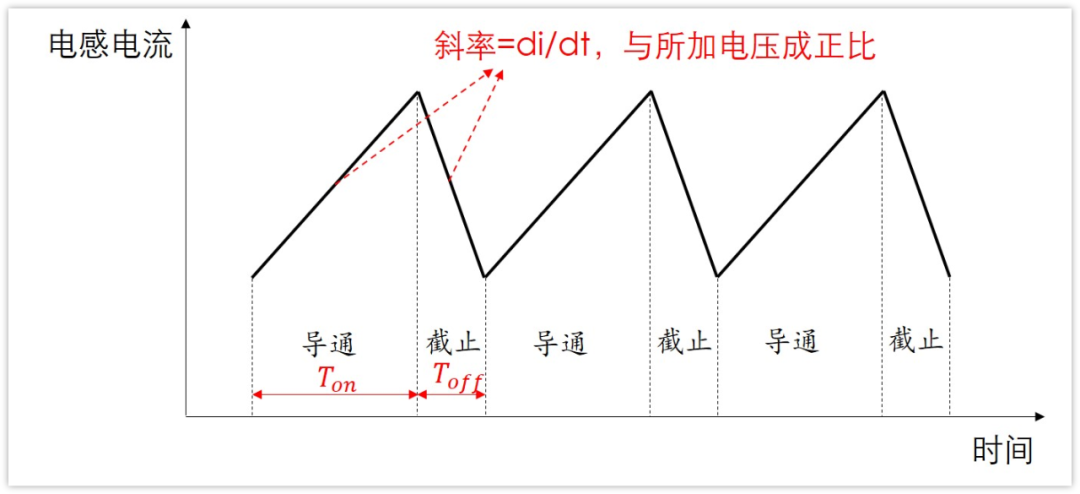
斜率與電壓成正比,電感電流上升的高度與下降高度又相同,那上升時間不就和電壓成反比了嗎?
所以,自然就有了:
Ton/Toff=(Vo+Vd-Vi)/Vi
我們變換一下,就得到了江湖所傳的“伏秒法則”

再根據T=Ton+Toff=1/f
我們可以分別求得導通時間,關斷時間,占空比。

好,這里,我們已經推出了第一部分公式。
其實從這里我們可以看到。
占空比與電感量L沒有關系,與負載電流的大小也沒有關系,只跟輸入輸出電壓有關系。
功率電感選擇
我們電感選型首先需要考慮兩個參數,電感感量和電感電流。
電感感量又決定了電感紋波電流的大小,為什么呢?
還是因為U=Ldi/dt,di/dt=U/L=電流變化斜率
所以,當我們確定了輸入輸出電壓,那么電感兩端的電壓就是固定的,那么電感電流變化斜率與電感量成反比,電感越大,斜率越小。
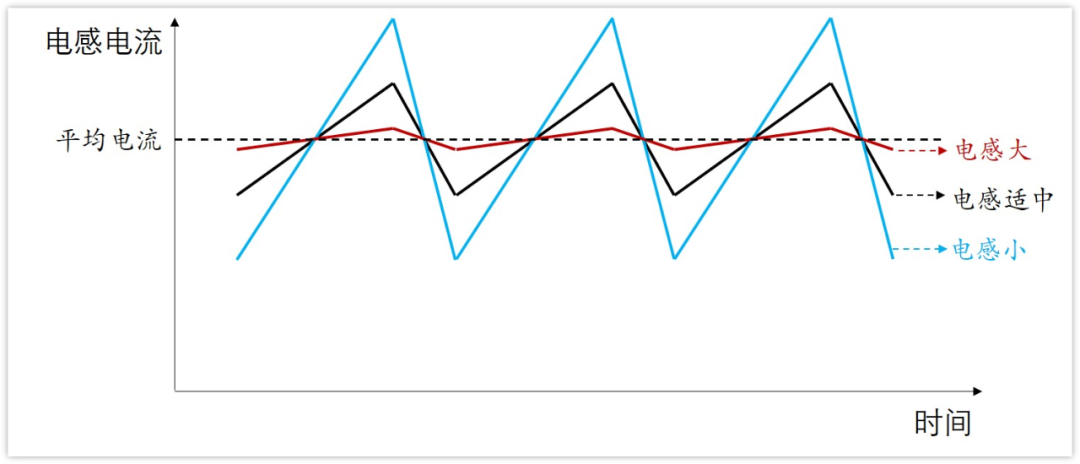
一般來說,電感感量的確定,是讓電感的紋波電流△IL等于電感平均電流的20%-40%之間。
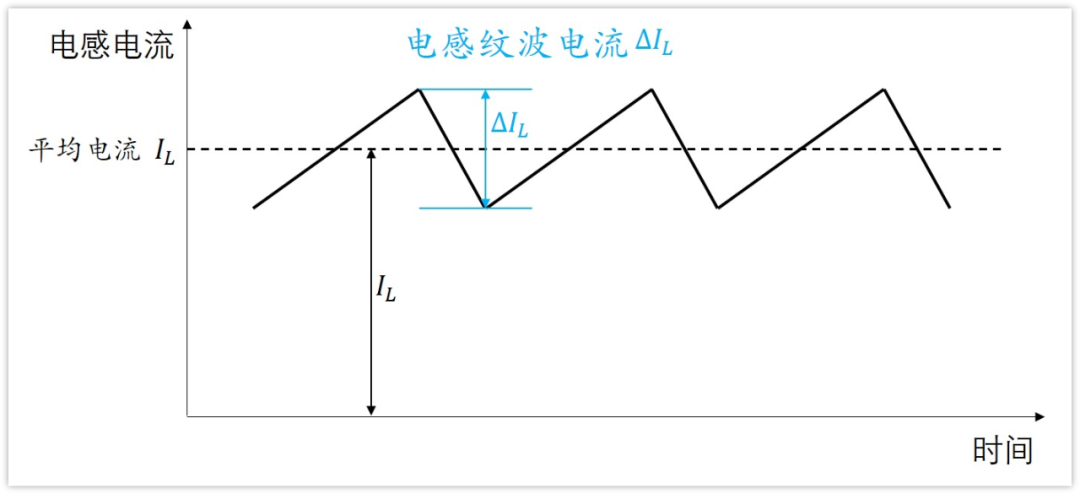
那為什么會這樣呢?電感過大或過小會有什么影響?
如果電感感量過小,那么電感紋波電流會比較大,即流過電感電流的峰值會很高,電感飽和電流就要很高。如此同時,過大的電流,在開關切換時,會導致EMI問題會更加明顯。
如果電感感量過大,那么電感電流紋波會比較小,會導致動態響應變差。
啥叫動態響應變差?
就比如輸出一直是1A的電流,某個時刻,負載從需要1A的電流變成突然需要5A的電流。這個時候,如果電感過大,電感電流充上來需要較長時間,那么電感電流需要很多個開關周期才能升到5A,這期間,負載所需要的5A電流主要來源于輸出濾波電容的放電,會導致輸出電壓跌落比較多,有可能出現故障。
簡單說,就是這個boost不能及時響應負載電流的快速變化。
好,我們下面來求合適的電感量
首先先求電感的平均電流IL
輸出電壓是Vo,輸出電流是Io,輸入電壓是Vi,那么根據能量守恒定律。
輸入功率*n=輸出功率。(n為效率)
輸入功率,就是電源的輸入電壓Vi乘以平均電流,顯然,從boost拓撲結構上看,電源的所有電流都會流過電感,那么這個電源輸出的平均電流也就是電感的平均電流IL。
即,Pi=Vi*IL
輸出功率
顯然,就是Po=Vo*Io
Pi*n=Po
即Vi*IL*n=Vo*Io
那么IL=Vo*Io/(Vi*n),估算時可以取n≈80%
我在有一些文件里面看到boost電感平均電流用這個公式計算:
IL=(Vo+Vd)*Io/Vi
這個公式怎么來的呢?
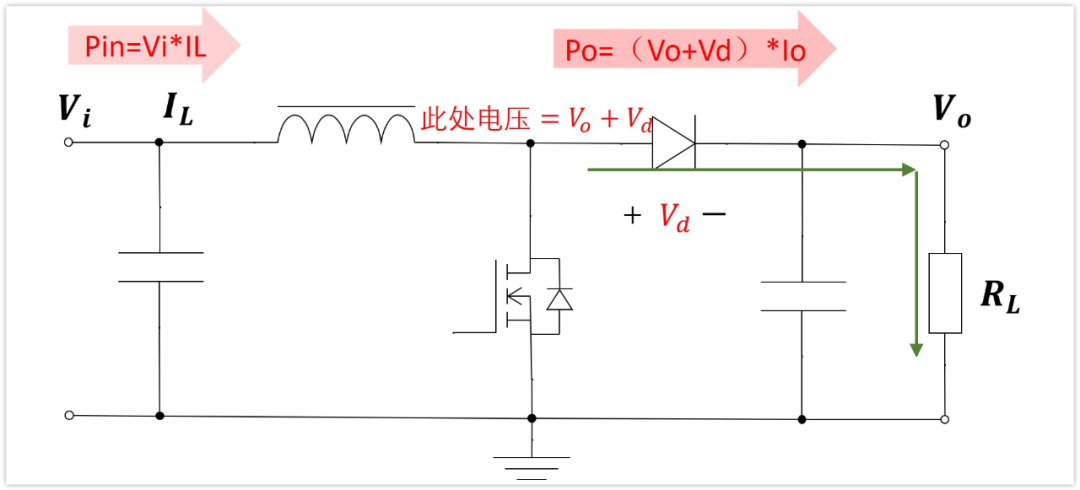
這個公式是假設只有二極管有損耗的,忽略其它的損耗。
如上圖,穩態時,輸出端電容是不耗電的,電壓也不會變化,所以其平均電流為0,也就是說,流過負載的電流,全部從二極管過來。所以二極管的平均電流也是Io,導通壓降是Vd,那么二極管的平均功率是Pd=Io*Vd。
所以有:
Po=P負載+Pd
即:Pi=Vi*IL=Io*Vo+Io*Vd
也就是:IL=(Vo+Vd)*Io/Vi
對于這個Boost來說,二極管的損耗是占比比較大的,估算確實可以采用這個公式。不過我們需要記住,這個公式僅僅考慮了二極管的損耗。
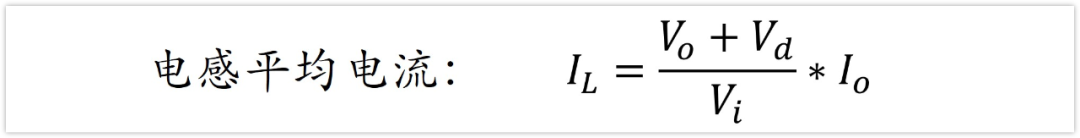
我們文章后面就用這個公式來計算吧。
其次,我們來求電感的紋波電流△IL
從前面知道,電感電流就是個三角波,在開關導通時電感電流增大,在關斷時,電感電流減小。
那紋波電流的大小求起來就簡單了,就等于在開關導通時電感電流增大的值,也等于關斷時電感電流減小的值。
我們就計算其中一個,計算開關導通時電感電流增大了多少吧。
這個也非常easy,開關導通,電感兩端電壓是Vi,導通時間Ton前面已經求出來了。
根據U=Ldi/dt就可以求出電感電流紋波△IL=di
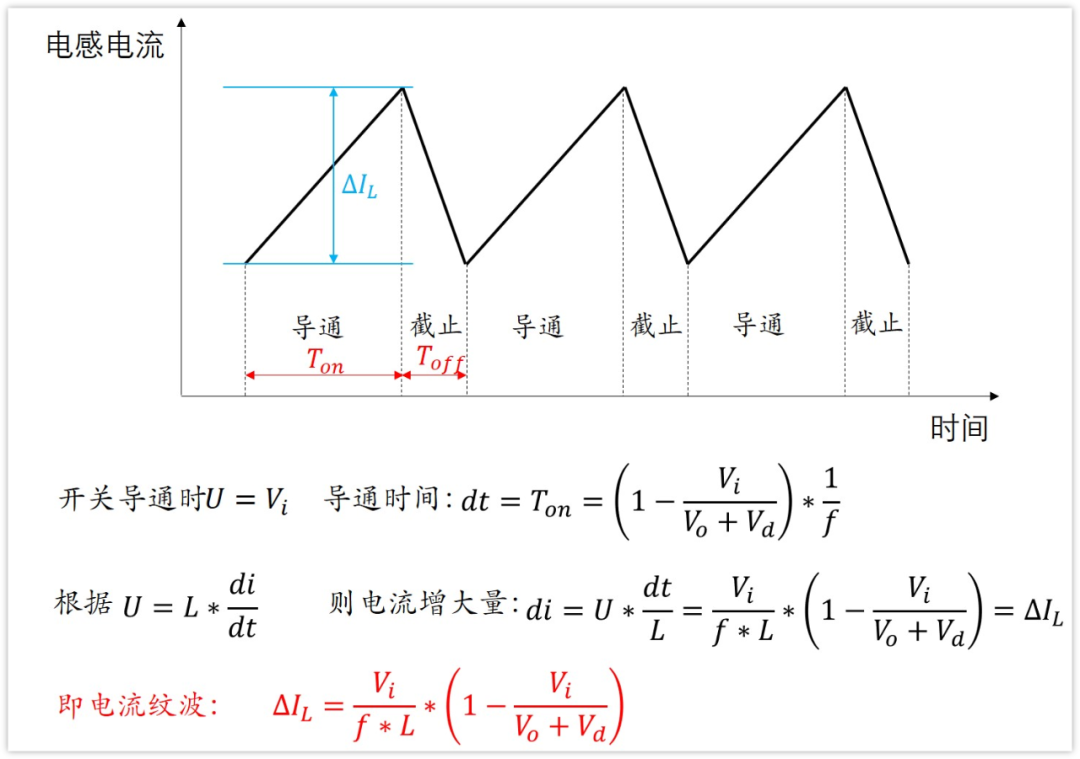
可以看到,電感電流的紋波跟負載電流的大小沒有關系。
現在我們已經寫出來了電感的平均電流IL,電感的紋波電流△IL,前面說了,△IL應該是IL的20%-40%為宜。
即:△IL=(0.2~0.4)*IL
根據這個等式,就能求得我們的電感值范圍了。
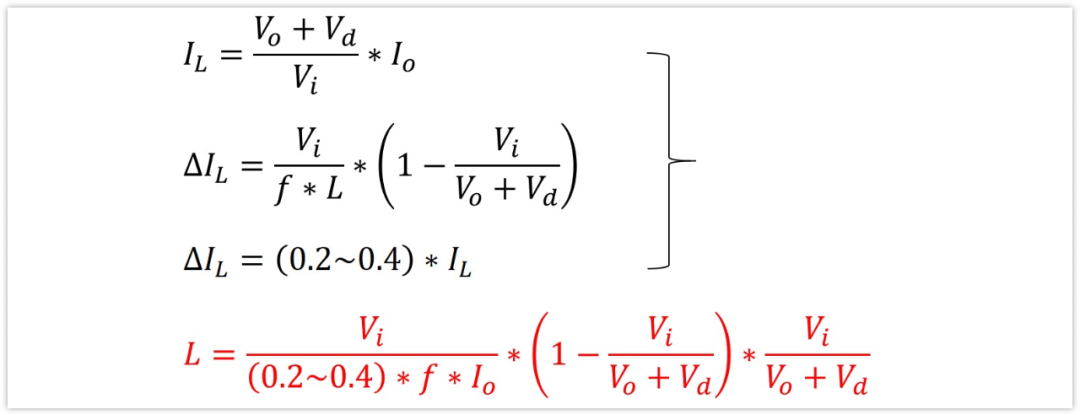
至此,我們已經求得了電感值的取值范圍,下面開始推導輸入輸出濾波電容的計算。
輸入濾波電容
我們在確定輸入濾波電容的時候,是有一個假設的,這個假設是什么呢?
輸入電源默認來自遠方,是沒法提供快速變化的電流的。
正是因為這一點,所以才有輸入濾波電容存在的必要,如果輸入電源總能快速響應Boost的電流的需求,那還要濾波電容干什么?
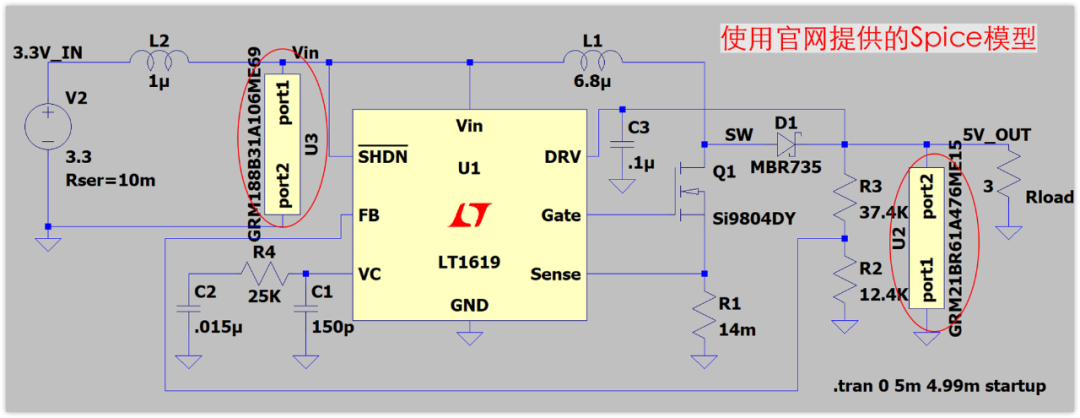
比如如果用LTspice仿真,會看到,仿真軟件自己的boost示例,都是沒有輸入濾波電容的。
下圖這個LT1619仿真電路,就是沒有輸入濾波電容的,這個是官方給出的示例,不是我畫的。
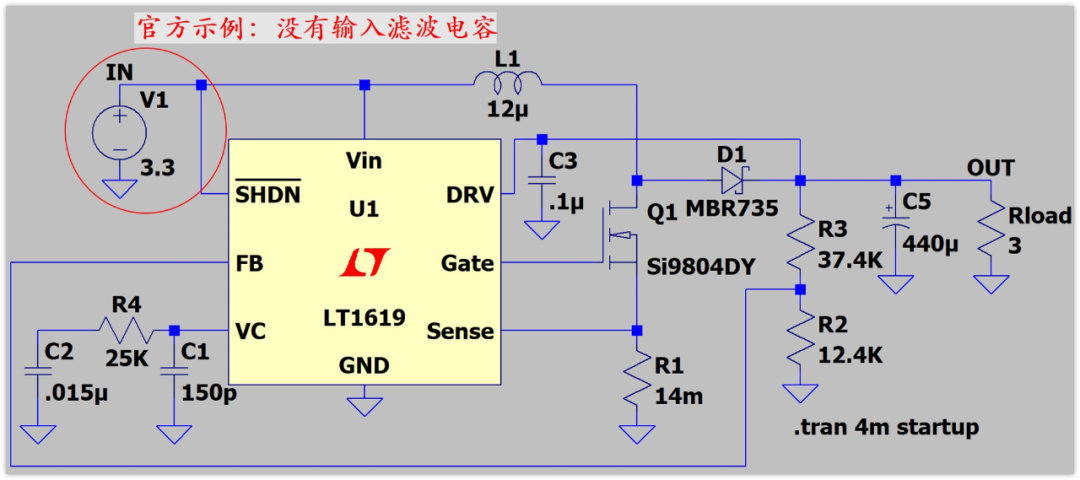
這個官方仿真示例不要輸入濾波電容,原因就在于它用的電源V1是電壓源。
電壓源在仿真軟件里面的意思就是,這個IN的電壓就是3.3V,永遠都是3.3V,不管后面電流咋變,反正我就能絕對的把Vin的電壓控制在3.3V,電流都能供上,你想要多大我就能提供多大,所以就不需要濾波電容了。
這一點,實際電路肯定做不到,所以需要輸入濾波電容來提供瞬態的電流需求。
那為什么實際輸入電源不能快速響應呢?
實際應用中,輸入電源可能距離很遠,有了很長的走線,走線越長,電感就越大,這里不再贅述。
總的來說,就是相當于遠處的電源接了一個電感到boost電路的輸入端,電感電流不能突變,也就是說輸入電源不能快速響應這個boost電流的需求。
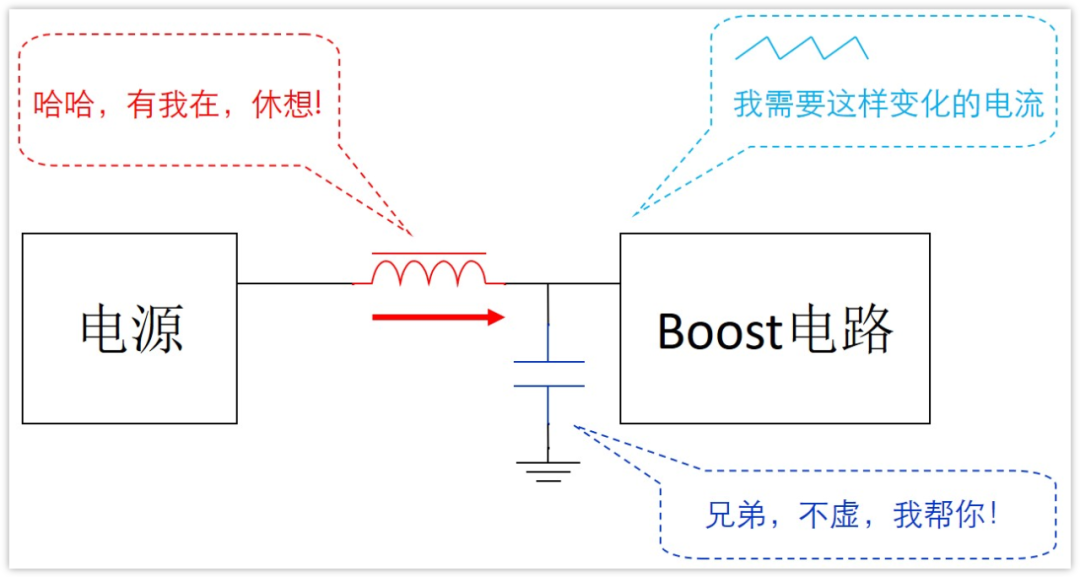
既然等效串聯了一個電感,而且Boost電路是開關電源,頻率大概在幾百Khz,周期也就幾us左右。那么在這一個周期之內,我們可以把電源輸入過來的電流看作是恒定不變的。
當然,肯定有人會說,如果我的電源輸入很近,可以快速響應,那就不對了呀?怎么電流能是恒定的呢?
這想法自然沒問題。
事實上,即使是電感,那也是阻礙電流的變化,并不是完全讓電流不能變化,所以對于動態的電流需求,還是能響應一點的。當然,線路電感越大,就越不容易馬上響應,能提供的電流波形也就越平。
但是呢,我們沒法控制這個線路的電感有多大,或者有的電路,電源上面更是直接使用了LC濾波器。
既然沒法控制,我們就按照最差的情況來處理,即在一個周期內,把電源輸入過來的電流看作是恒定不變的,Boost需要的動態電流完全由濾波電容來提供,根據這種情況選擇的輸入濾波電容,就可以滿足所有的情況了。
好,又說了一堆,回到我們的目標:計算輸入濾波電容容量。
輸入濾波電容是用來控制輸入電壓紋波△Vi的,下面來看如何根據△Vi得到輸入濾波電容Ci的大小。
我們先理清下思路,輸入電壓紋波就是輸入電容上面的紋波變化。電容上面的紋波變化可以分成兩個部分。
一個是電容放電或者是充電,存儲了電荷量發生了變化,這個變化會導致電壓變化,可以用公式Q=CUq來表示,Uq即是電壓的變化。
另一個是電容有等效串聯電阻ESR,電容充放電時有電流流過,電流流過ESR會產生壓降,這個壓降用Uesr表示吧。
所以,電壓紋波應該是:
△Vi=Uq+Uesr
1、電容電荷量變化引起的壓降Uq
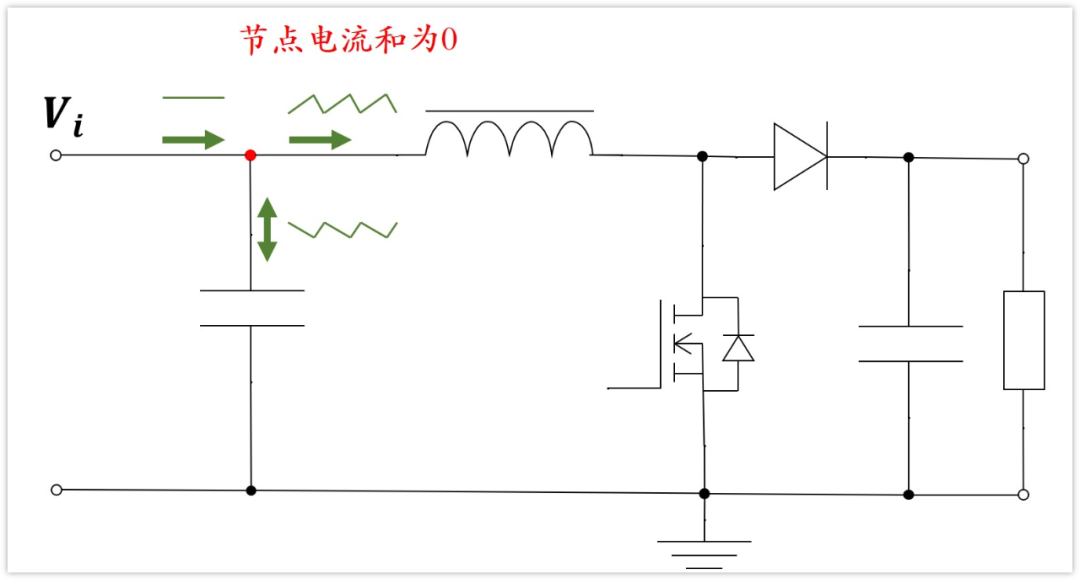
我們看輸入節點,這個節點的電流有3個,一個是來自電源輸入的,前面說了,在一個周期內,它可以看作是恒定的,一個節點是電容,另外一個節點是電感。
根據基爾霍夫電流定律,節點電流和為0,并且電源輸入的電流恒定,那么當電感電流的變化量必然等于電容電流的變化量,因為最終3者的和為0。
我們畫出三者的電流波形如下:
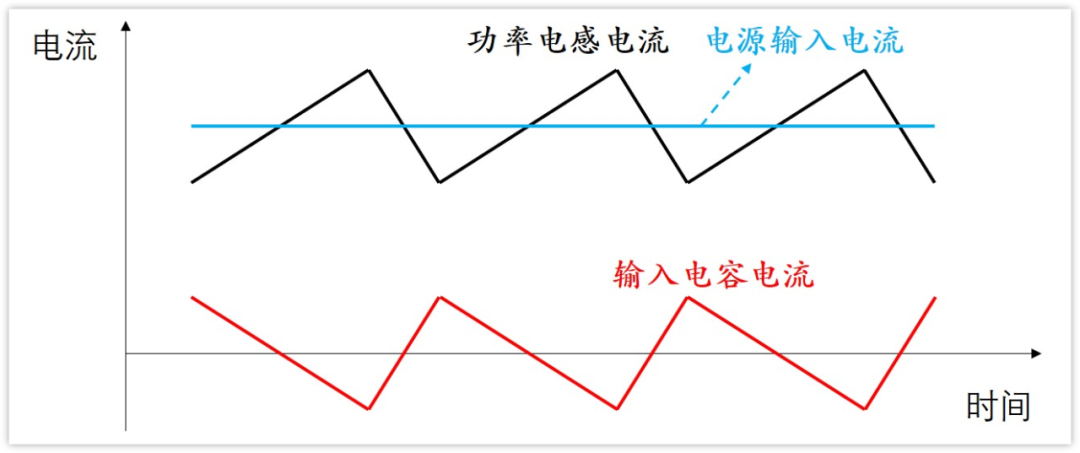
根據節點電流和為0,那么輸入電容的電流變化就是功率電感的電流變化(你增大時我減小,你減小時我增大)。我們從上圖也可以很直觀的看出來。
顯然,電容電流大于0時,電容在充電,電容電流小于0時,電容在放電。
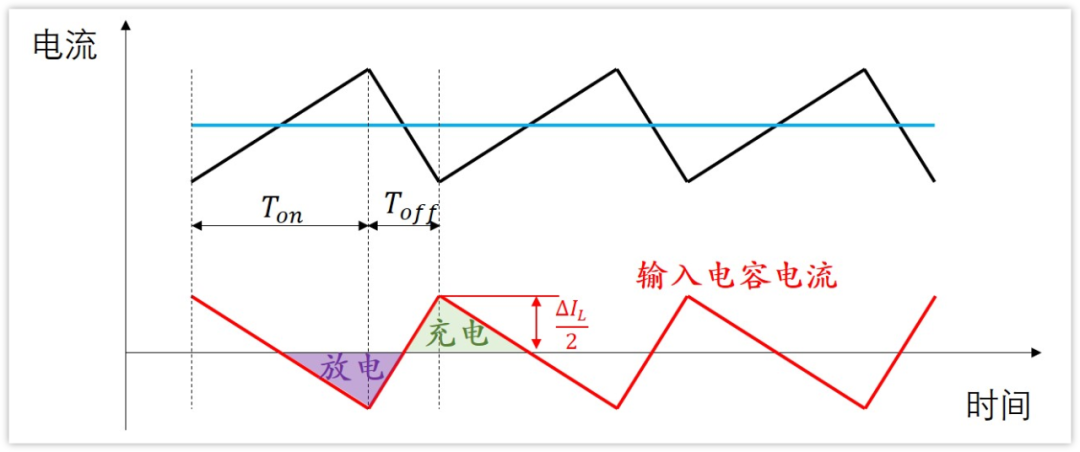
可以看到,電容充電和放電時間長度是一樣的,都是周期的一半,T/2。
那充放電的電荷量是多少呢?
放電的電荷量,等于放電電流i乘以放電時間t,不過放電電流不是恒定的。從前面知道,電容放電電流它等于電感電流的變化量,所以電容電流的變化量也是△IL。
需要注意,電容電流是在大于0時充電,電流小于0時放電,也就是圖中陰影部分,充電與放電的切換的時刻并不是開關導通與斷開的時候,而是在中間時刻。
然后電容放電/充電的總電荷量Q等于電流乘以時間,這不就是圖中陰影三角形的面積嗎?
三角形底部是時間,充電/放電時間等于T/2
三角形的高為電感紋波電流的一半,△IL/2。
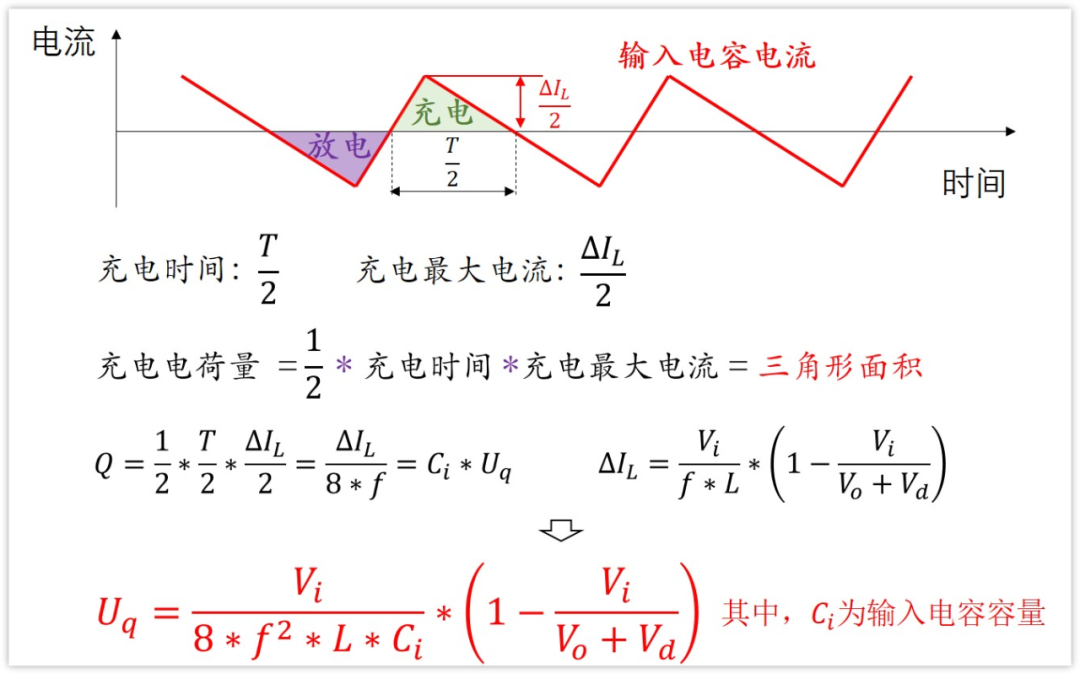
所以總放電量為Q=1/2*底*高
再結合Q=CUq,即可求得Uq了。
具體計算如下圖所示:
2、電流流過電容的ESR造成的壓降Uesr。
前面波形圖知道,電容的充電電流最大是△IL/2,放電電流最大就是-△IL/2,負號表示電流方向,方向的不同,引起的壓降的電壓也是相反的。
那么ESR引起的總的壓降是:
Uesr=△IL/2*ESR-(-△IL/2*ESR)= △IL*ESR
最終,我們求得Uesr的公式如下:

好,我們已經算出Uesr和Uq。
那么根據△Vi=Uesr+Uq,我們就可以△Vi的表達式了,如果知道△Vi,我們也能得到輸入電容Ci的大小或者是ESR了。

這個公式看著有點復雜,有兩個參數都跟電容本身有關系,ESR和容量Ci。
考慮到我們的電容實際使用情況
陶瓷電容ESR小,容量小,Uq對紋波起決定作用,所以可以近似△Vi=Uq
鋁電解電容容量大,ESR大,Uesr對紋波起決定作用,所以可以近似△Vi=Uesr
根據上面兩點,我們就可以去選擇合適的電容了。
陶瓷電容根據容量值去選
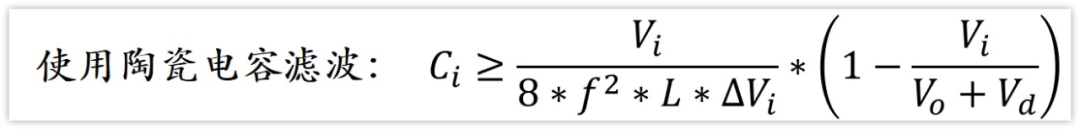
鋁電解電容根據ESR去選
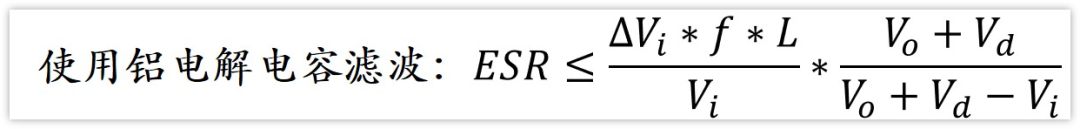
當然了,這一段話很多資料都有,但是很少有實際比較過Uq和Uesr的大小的,文章后面會做實驗來實際看看
好,現在輸入電容的理論計算已經搞定了,我們接著看輸出濾波電容。
輸出濾波電容
相比輸入紋波△Vi大小,我們可能更關心輸出紋波的大小,畢竟是要帶負載的。
同樣,紋波由電容電荷量變化和ESR決定。
1、電容電荷量變化引起的Uq
一個周期內,電容的充電電荷量和放電電荷量必然一樣,我們計算出其中一個就行了。顯然,放電的時候更好計算,因為放電電流就是負載電流,是恒定的,為Io=Vo/RL。
放電的電荷量等于容量乘以電容電壓的變化,也等于放電電流乘以放電時間,即:
Q=Uq*C=Io*Ton
根據這個公式,我們就可以求得Uq了。

2、電流流過電容的ESR造成的壓降Uesr
Uesr如何計算呢?
我們調出輸出電容的電流波形就知道了。
這個波形我解釋一下。
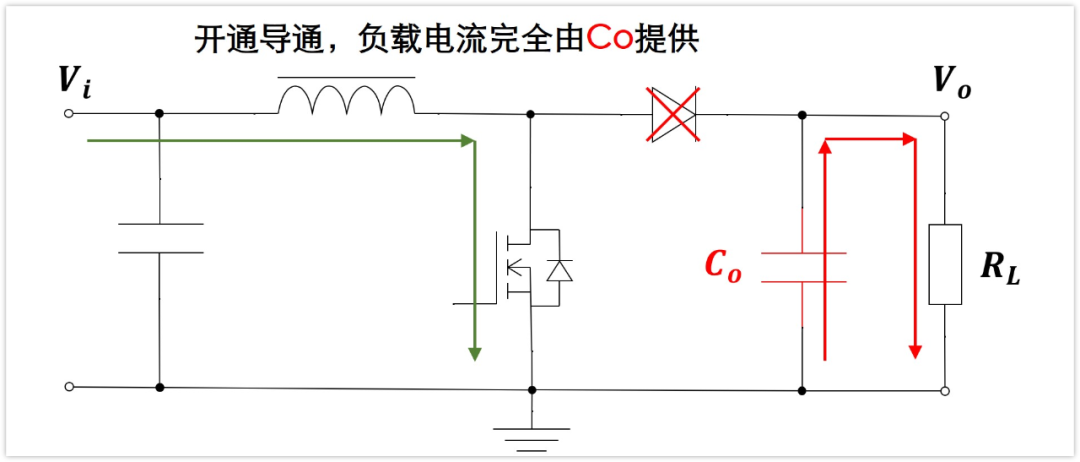
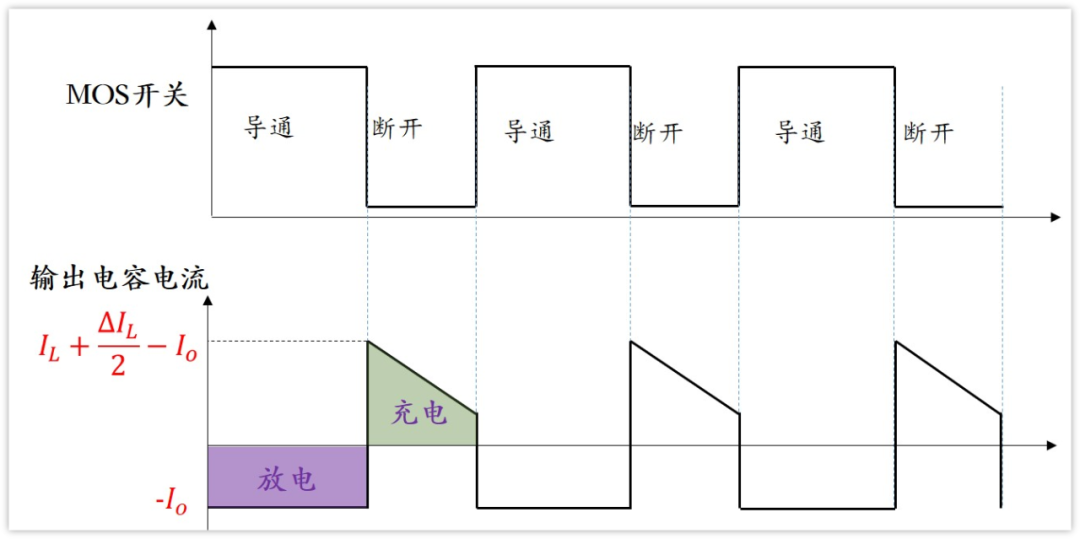
在開關導通的時候,二極管不導通,負載的電流為Io,完全由輸出濾波電容提供,即濾波電容的放電電流也為Io,而且還是在導通時間里面恒定不變的。
在開關從導通切換到斷開時,電感的電流已經是充到最大的,因為先前開關導通時電感一直在充電,所以切換時電感電流最大,且等于電感平均電流加上紋波電流的一半,即為IL+△IL/2。切換時,這個已經充好的電流會通過二極管給負載供電,負載電流為Io。同時,電感還要給電容進行充電,根據節點電流和為0,那么電容的充電電流就是電感充到最大的電流減去負載的電流,即IL+△IL/2-Io。
在開關斷開之后,電感電壓反向了,所以電感電流持續減小,也就是說二極管的電流持續減小,而負載電流不變,所以輸出濾波電容的電流持續減小。
根據上圖,在開關切換之前,電容的電流為-Io,那么ESR兩端的電壓是-Io*ESR。
在切換之后,電容的電流立馬反向,為IL+△IL/2-Io,那么ESR兩端的電壓是(IL+△IL/2-Io)*ESR,兩者相減,就是ESR上電壓變化量,也是ESR產生的紋波電壓大小。
即
Uesr=(IL+△IL/2-Io)*ESR-(-Io*ESR)
= (IL+△IL/2)*ESR,

好,我們已經算出Uesr和Uq。
那么根據△Vo=Uesr+Uq,我們就可以△Vo的表達式了,如果知道△Vo,我們也能得到輸出濾波電容Co的大小或者是ESR了。
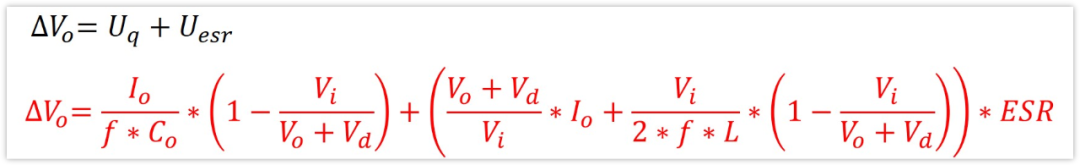
與輸入濾波電容一樣,考慮到我們使用的電容類型。
陶瓷電容ESR小,容量小,Uq對紋波起決定作用,所以可以近似△Vo=Uq
鋁電解電容容量大,ESR大,Uesr對紋波起決定作用,所以可以近似△Vo=Uesr
根據上面兩點,我們就可以去選擇合適的電容了。
陶瓷電容根據容量值去選
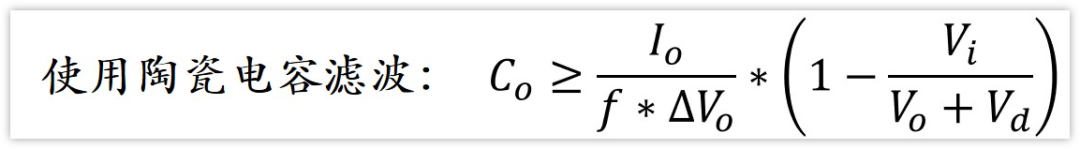
可以看到,公式里面沒有電感L,也就是說,如果使用陶瓷電容濾波,增大電感量對輸出紋波不起作用,不要傻傻去增大電感啦。
鋁電解電容根據ESR去選
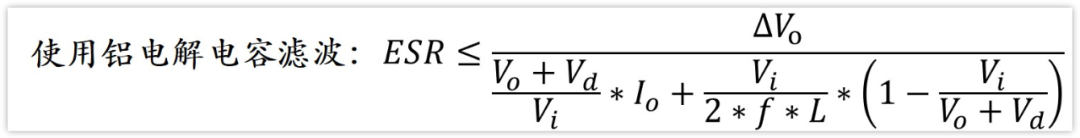
不容易啊,現在公式都推導完成了。
下面進入實驗環節,以此來檢驗上面的公式是否正確
實驗驗證
實驗已知條件及紋波要求:
使用boost芯片LT1619。
開關頻率是f=300Khz
輸入電壓Vi=3.3V
輸出電壓Vo=5V
二極管使用MBR735,導通電壓約為:Vd=0.5V
負載R=3Ω,負載電流Io=Vo/R=1.667A
輸入紋波要求:△Vi≤30mV
輸出紋波要求:△Vo≤50mV
1、首先需要確定電感值L
根據前面推導出的公式計算,可得,電感的取值范圍為:
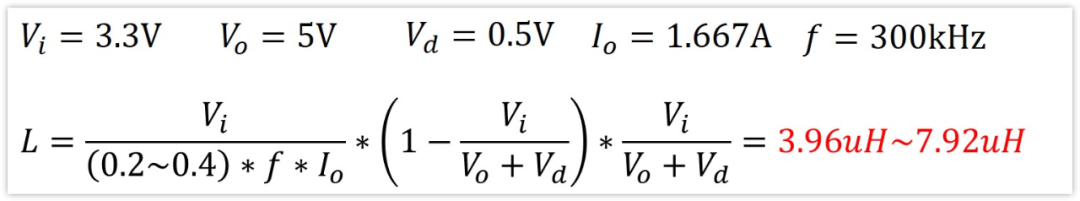
我們求得電感的范圍是3.96uH~7.92uH。
我們取現實中常用的電感值L=6.8uH吧。
當然,我們現實中電感選型也要考慮電感的飽和電流是否足夠,飽和電流要大于電感會流過的最大電流值ILmax,并且要留有一定的裕量。
顯然,這個ILmax=IL+△IL/2。
我們根據前面的公式計算得ILmax=3.1A
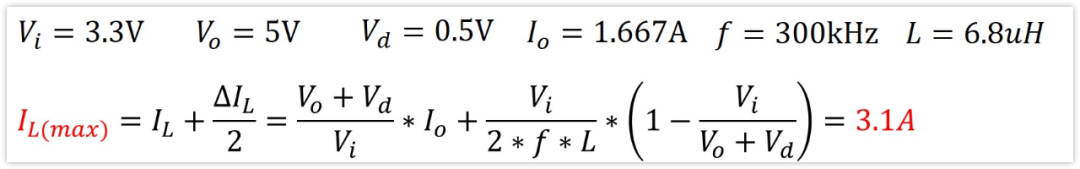
2、如果使用陶瓷電容濾波
先看輸入濾波電容Ci:
Ci的值計算結果(忽略了ESR)如下:
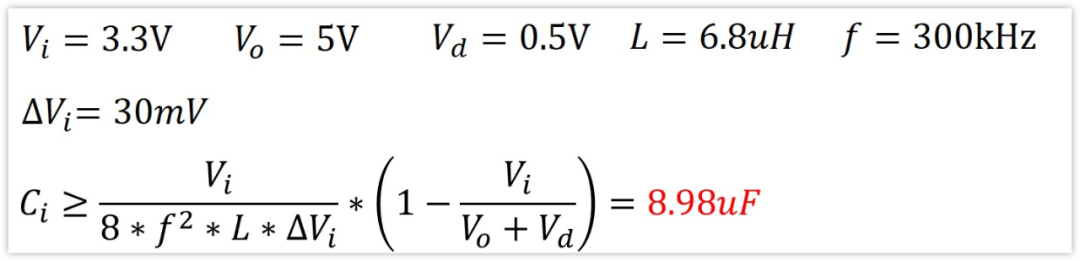
可以看到,Ci要大于8.98uF。
我們取現實中常用的電容值Ci=10uF吧。
并且,在Ci=8.98uF時紋波△Vi=30mV,那么Ci=10uF時,紋波是△Vi=26.94mV,我們記住這個值,后面仿真對比使用。
再看輸出濾波電容Co:
Co的值計算結果(忽略了ESR)如下:

可以看到,Co需要大于44.45uF。
我們取現實中常用的電容值Co=47uF吧
并且,在Co=44.45uF時紋波△Vo=50mV,那么Co=47uF時,紋波是△Vo=47.29mV,我們也記住這個值,后面仿真對比。
仿真驗證:
好,現在電感L,輸入濾波電容Ci,輸出濾波電容Co都有了
輸入電壓:3.3V
輸出電壓:5V
L=6.8uH
Ci=10uF
Co=47uF
我們LTspice仿真電路圖如下:
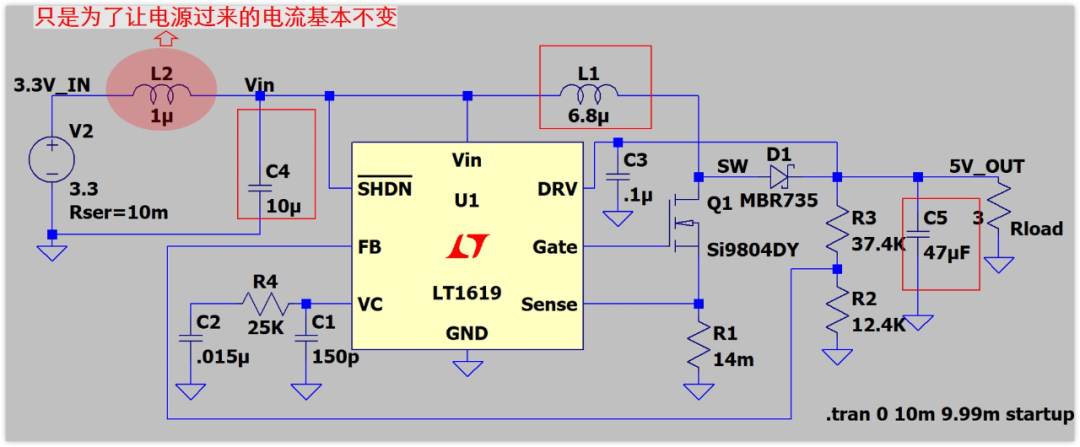
有個問題先解釋一下,在電源輸入端我加了一個1uH的電感L2,就是為了讓輸入電源過來的電流基本恒定,模擬前面說的最差的情況(電源比較遠)。若果沒有這個L2,那么Vin就是穩壓源的電壓,絕對的穩定,沒有紋波的。
我們看仿真結果:
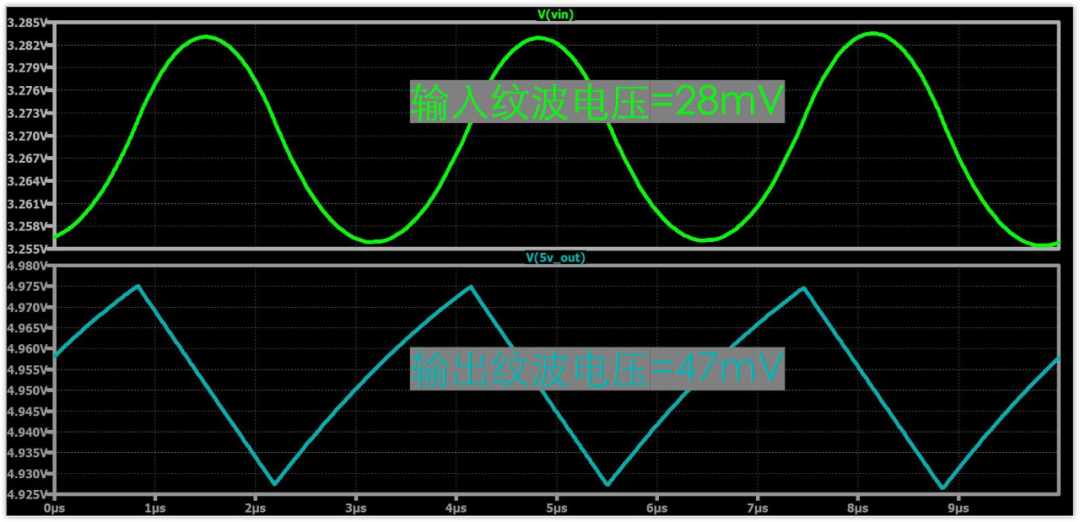
輸入紋波電壓計算值為26.94mV,仿真值為28mV
輸出紋波電壓計算值為47.29mV,仿真值為47mV
可以看到,仿真的結果與計算值非常接近,也就驗證了計算公式的準確性。
這里插一點,為了方便同志們學習boost,我將關鍵點的電壓,電流波形截圖出來了,分析Boost可以參考
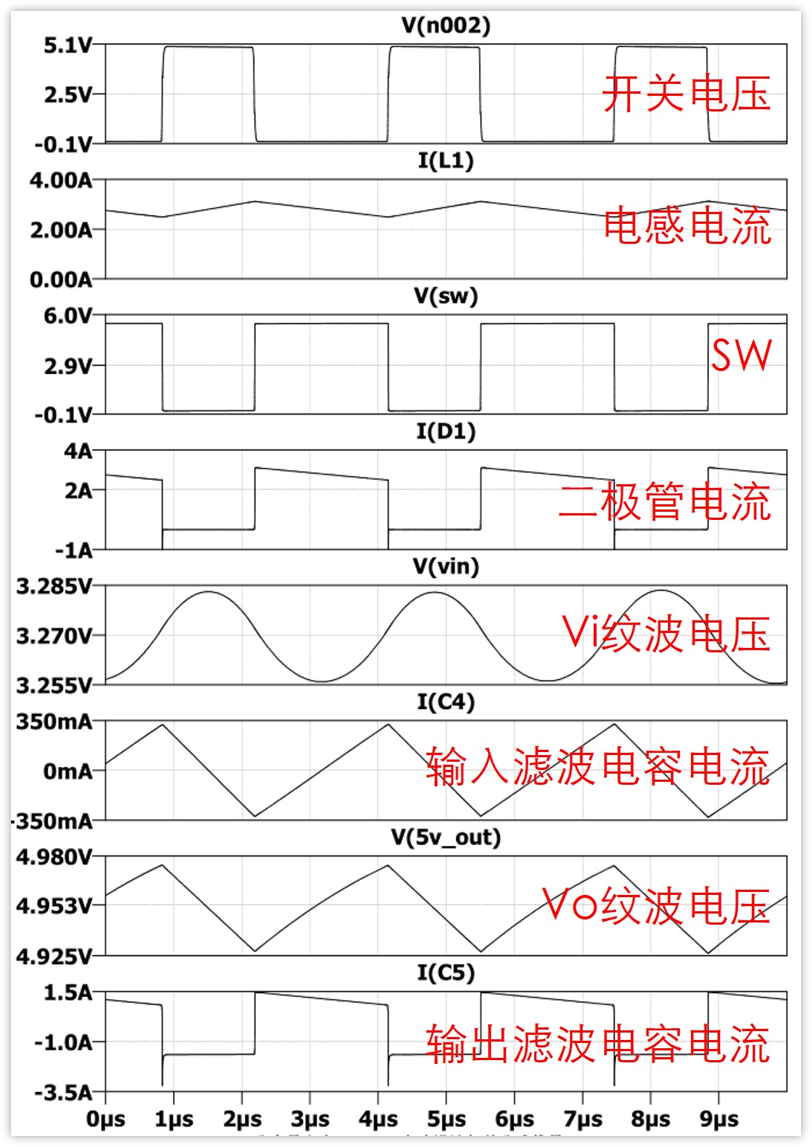
有一點需要說明下:圖中二極管的電流和輸出濾波電容的電流都有一個向下的尖峰,這個尖峰是因為二極管的反向恢復時間造成的
即二極管電壓反向,它不能馬上恢復截止功能的,需要時間,這個時間就是反向恢復時間,在這個時間里面,二極管可以通過較大的反向電流,所以就有了較大的反向電流存在。
文末會給出仿真的源文件,感興趣的同學可以自己玩一玩,不同類型的二極管反向恢復時間不同,向下的尖峰也是不一樣的,這里就不再展開了。
我們繼續
陶瓷電容ESR
陶瓷電容我們都通常說ESR很小,可以忽略,前面的計算也是忽略。
不過想必大家也肯定想過,總說ESR小,影響小,那到底有多小?
我們上面用了兩個陶瓷電容,10uF和47uF,那我們查查這兩個電容的ESR情況。
這里我找了兩個型號:
10uF/10V:GRM188B31A106ME69
47uF/10V:GRM21BR61A476ME15
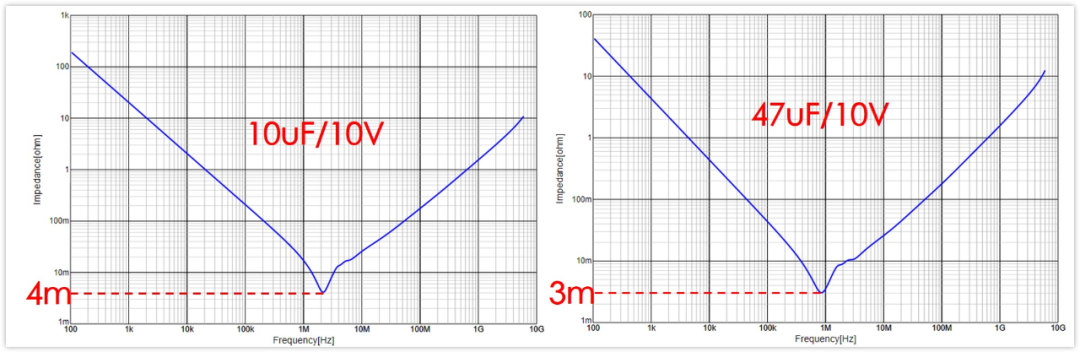
10uF電容的ESR是4mΩ,47uF電容的ESR是3mΩ
我們還是先計算一下,ESR對紋波的貢獻有多少。
輸入10uF電容的ESR是4mΩ,引入的紋波電壓是
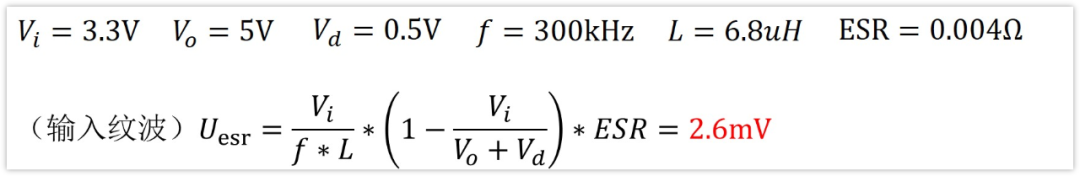
相比于容量引起的紋波26.94mV,這個約為十分之一左右,確實很小。
兩者加起來,新的△Vi=26.94+2.6=29.54mV
輸出47uF電容的ESR是3mΩ,引入的紋波電壓
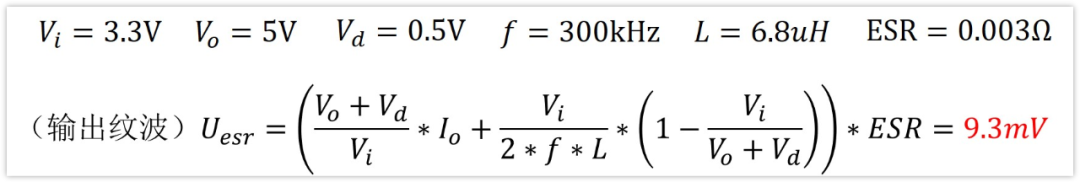
相比于容量引起的紋波47.29mv,這個也是比較小的,大約是五分之一吧,但似乎達不到可以忽略的地步。
兩者加起來,新的△Vo=47.29+9.3=56.59mV
下面我們把ESR加入到電路中
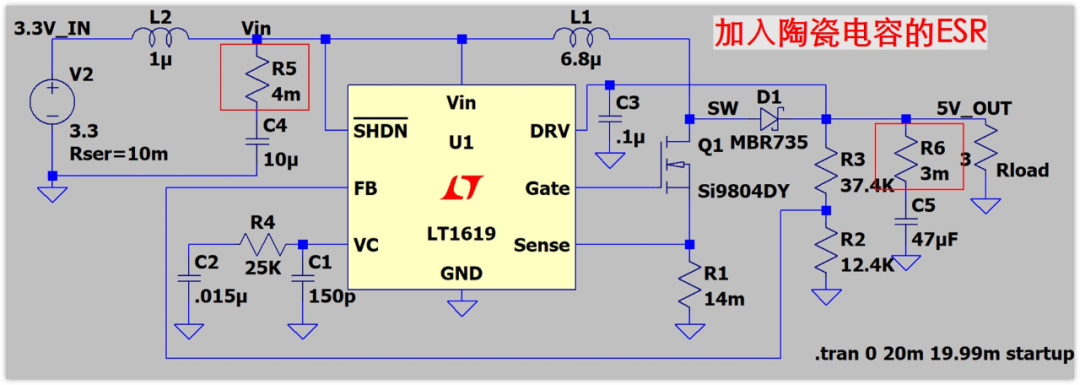
運行一下,結果如下圖:
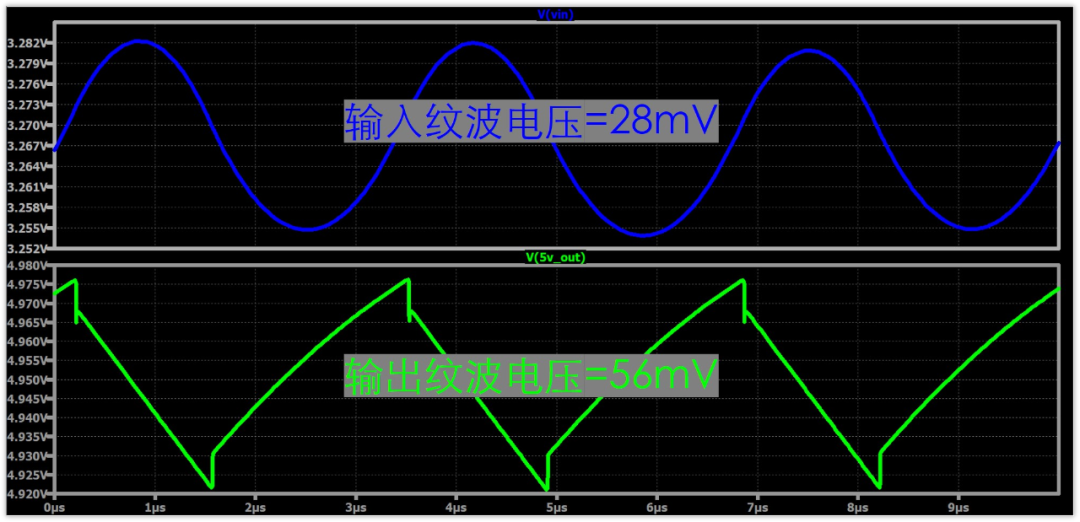
加入ESR之后,可以看到,輸入紋波電壓還是28mV,基本沒有變化,不過與計算值29.54mV也差得不多。
這個輸入紋波加了ESR基本沒變化,確實是有原因的。
原因是因為輸入濾波電容的電流是變化的,我們計算的是Uesr的最大值,出現最大值的時刻并不在電容放電完成后的時刻(放電完成時Uq產生的壓降最大)。放電完成的時刻電容電流為0,ESR上面沒有壓降,所以基本就不變了,所以咱們看到的就是△Vi沒變化。
不過這個也不用細細區深究,本身Uesr太小了,影響不大。
這個問題在輸出濾波電容上面不會出現,因為輸出濾波電容是一直有電流的,這個可以從前面的波形圖看出來,所以最終的紋波,是可以將Uesr和Uq直接相加的
因此,我們可以看到,輸出濾波電容的紋波電壓仿真是56mV,與計算值56.59mV也是非常接近的,增加ESR后,紋波實打實增加了9mV左右。
而且,可以看到,輸出紋波在底部有一個突然的上升,這個就是電容電流突然變化,在ESR上面產生的壓降,大致也可以看到是9mV左右。
另一方面,這個波形與我們實際測試想比,還差了點啥?
實際測試經常有毛刺對吧,這里面看不到
仿真軟件,其實就是使用計算機進行數學計算,一般是不會出錯的,不準確肯定是模型不夠準確。
很容易想到,仿真圖里面電容等效一個理想電容和ESR電阻串聯構成,這跟真實的電容還是有差距的,怎么說也會有寄生電感存在吧。
我就不手動添加寄生電感了,直接使用廠家提供的電容spice模型吧。
仿真結果如下圖:
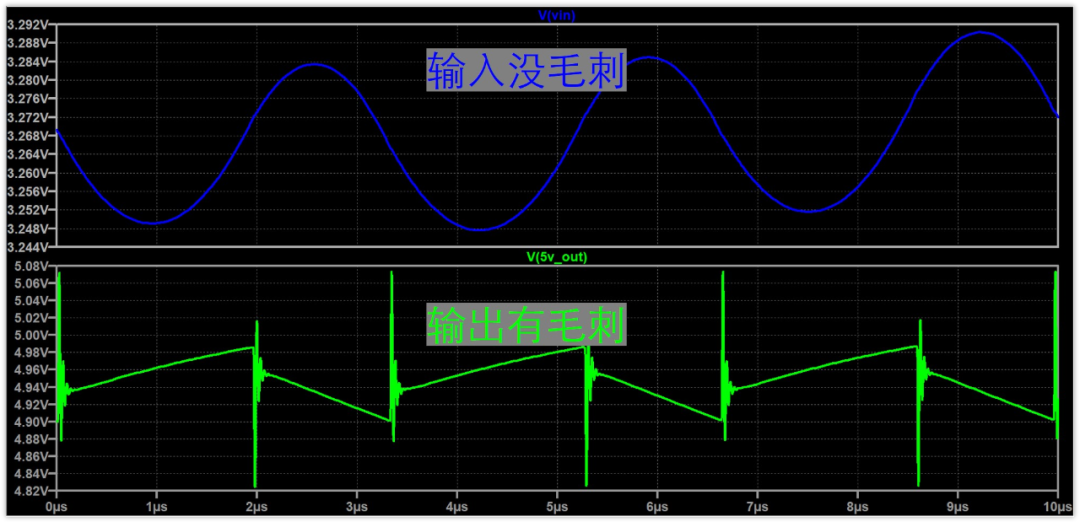
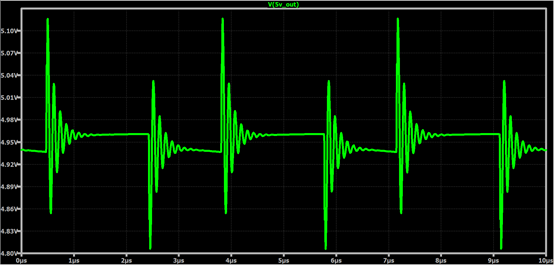
輸入還是沒毛刺,輸出毛刺出來了,是不是有點兒意思呢?
算上毛刺,輸出紋波大小大概是250mV,這是預想的50mV的5倍。
先來看毛刺吧,毛刺是怎么出來的呢?
其實這個很容易,從前面分析知道,輸入電容和輸出電容的電流波形如下:
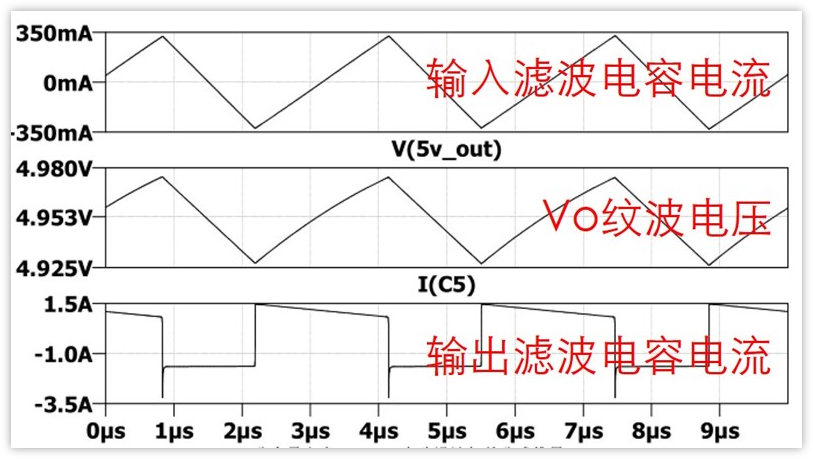
由圖可知,輸入濾波電容的電流是沒有突變的(有拐點,但是是連續的),而輸出濾波電容的電流是有突變的(由負突然變為正)。
我們知道電容都是有各種寄生參數的,自然也有寄生電感存在,突變的電流意味著di/dt很大,這必然會在寄生電感上面產生高的電壓,也就是圖中的毛刺。
如何搞定這個毛刺?
去掉是不可能的,這輩子都不可能,只能降低幅度。
我們在輸出端加一個100nF小電容,電路圖變為如下:
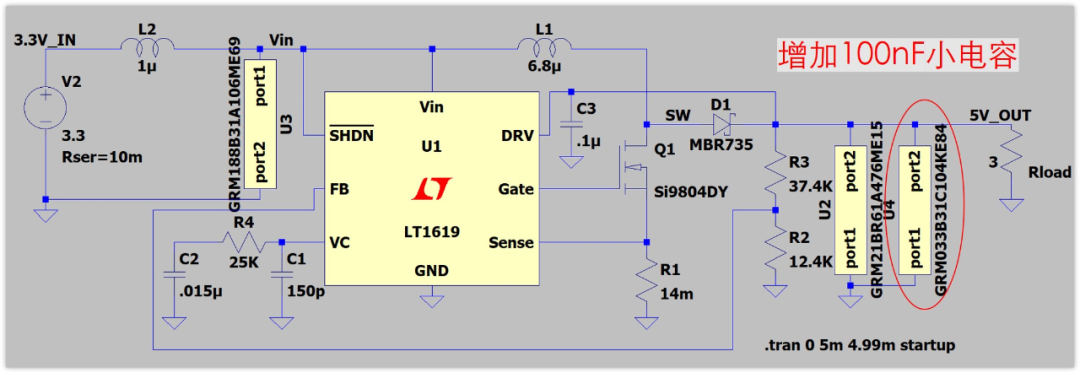
輸出紋波如下:
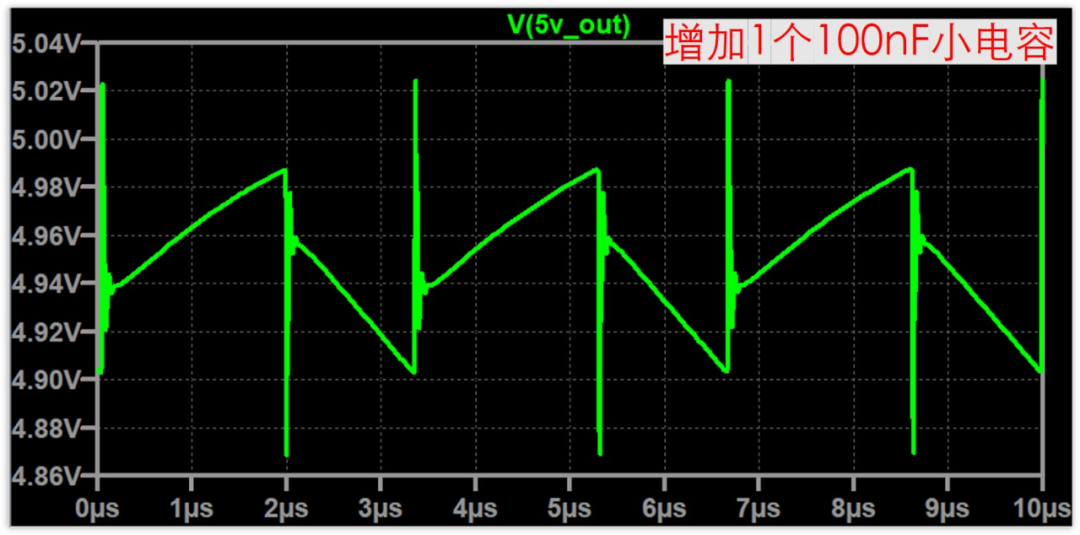
可以看到,毛刺下降了,總的紋波從250mV下降到了160mV左右,效果是有的。
毛刺還是有點大,怎么辦?
簡單啊,再增加一個100nF電容,總共放兩個100nf濾波電容,是這樣嗎?
仿真一下,發現紋波變成了110mV左右,確實有減小。
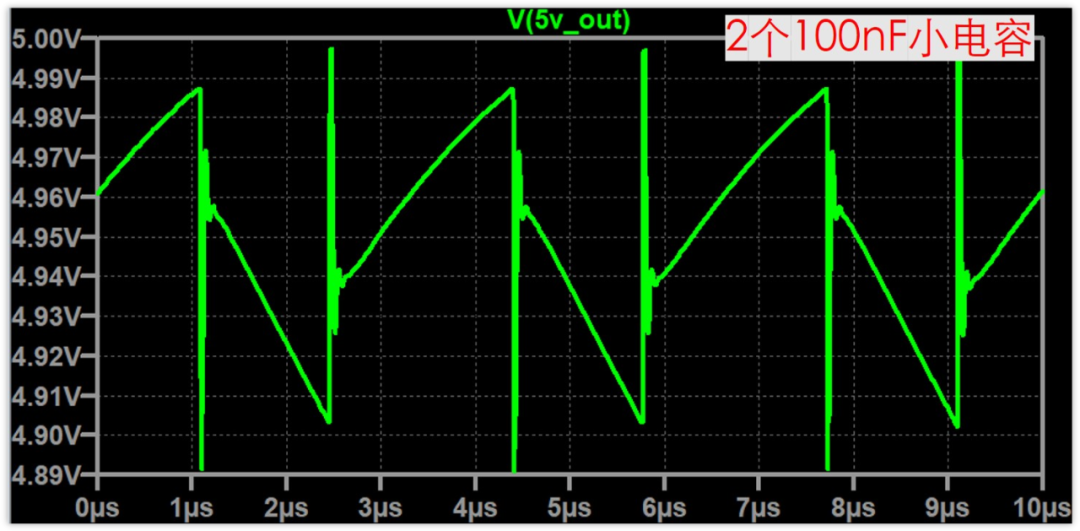
所以,我們想要降低毛刺,可以多并聯幾個100nF的小電容。
想必到這里,應該知道boost后面為什么有大電容也有小電容了吧。
大電容決定了整體紋波的大小(去掉毛刺剩下的),小電容是為了降低毛刺的。
除了毛刺這個問題,我們發現,使用了spice文件構建的電容之后,輸入紋波和輸出紋波都變大了,而且還是變大不少的。
輸入紋波從28mV變到了35mV。
輸出紋波從56mV變到了83mV(不算毛刺)。
使用spice文件生成的電容模型的仿真結果肯定是更為準確的,它是廠家提供的,能更真實的還原電容的特性。
我們前面的計算公式是從拓撲結構推出來的,只考慮了電容的容量C和ESR,所以是一個理想的結果。
雖說算出來與實際結果有差距,但是還是有其意義的,至少我們知道了紋波大概在多少mv,我們留好裕量就好了。
那這個裕量留多少?2倍嗎?
比如計算輸出濾波電容47uF,但是仿真紋波比50mV大不少,達到了83mV,那我使用100uF的濾波電容,容量提升了2倍,應該可以控制在50mV以內吧。
選用標稱值為100uF/10V的MLCC陶瓷電容可以嗎?
答案是:no!no!no!
陶瓷電容有一個特性,就是容量會隨所加的電壓發生變化,這個變化很大!!
這個特性叫直流偏壓特性,MLCC有這個特性,鋁電解電容沒這個。
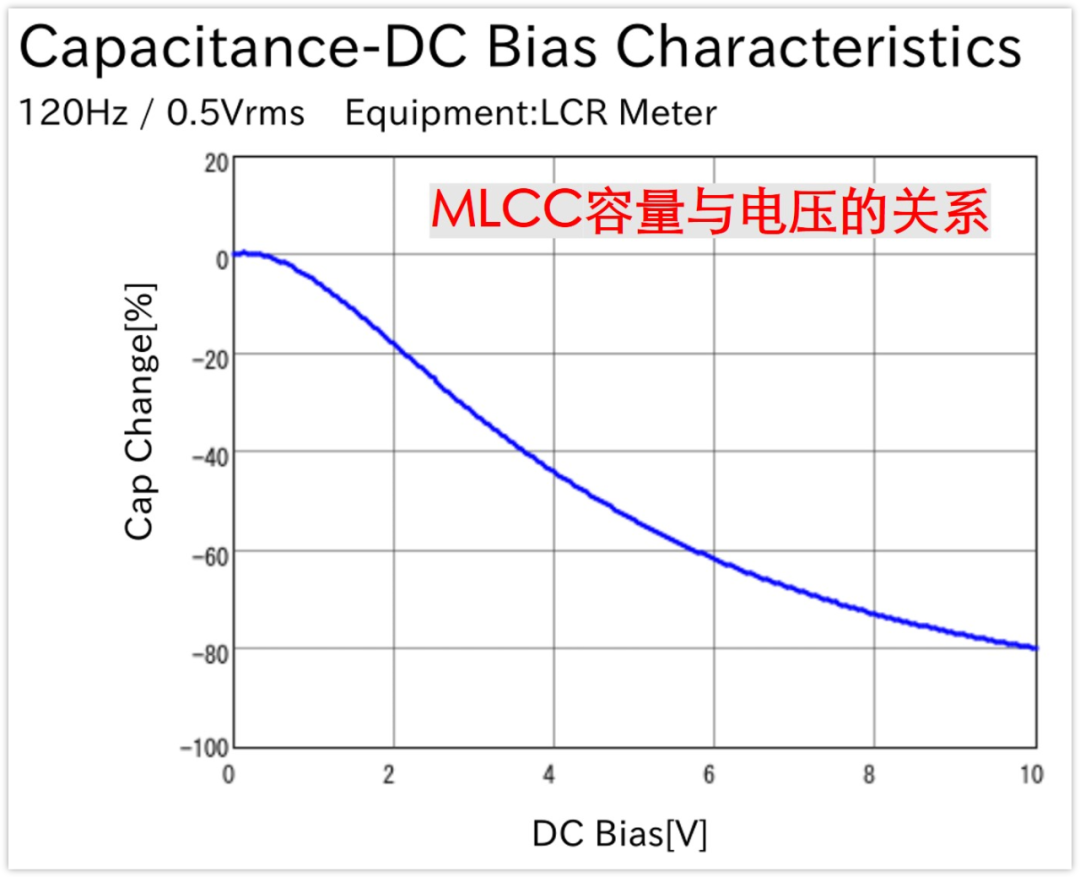
上圖是GRM32ER61A107ME20(100uF/10V)的電容曲線。
我們輸出電壓是5V,在5V時,這個電容的實際容量只有標稱值的50%,也就是說只有50uF左右。
所以,選擇100uF/10V是不行的,應該要選擇更大容量的電容,比如200uF。或者是2個100uF的電容并聯,這樣真正的有效容量才會有100uF。
另外一方面,這個是耐壓10V的電容,在5V使用時,有效容量只剩下50%,如果輸出是7V,容量就只剩下30%了,也就說必須選擇更大容量的電容。
或者說選用耐壓值更高的電容,這樣有效電容量更高。
關于Boost使用陶瓷電容濾波,我們小結一下:
1、我們使用公式計算出的電容量大小,往往是偏小的,真實紋波要比計算值要高一些。
2、MLCC陶瓷電容的直流偏壓特性,因此使用時,往往實際容量要比標稱值小很多。
3、boost輸出會容易產生高頻毛刺,需要加小電容降低毛刺。
因此,設計時,真正的電容要比計算的大,紋波要求嚴格的地方,可能需要4-5倍。
說完了使用陶瓷電容的情況,那使用鋁電解電容會怎么樣呢?
3、使用鋁電解電容濾波
還是先來計算一番
鋁電解電容的ESR比較大,所以紋波主要由ESR決定,因此我們忽略容量的影響。
輸入濾波電容ESR

即輸入濾波電容的ESR如果控制在46mΩ,那么輸入紋波電壓可以控制在30mV
輸出濾波電容ESR
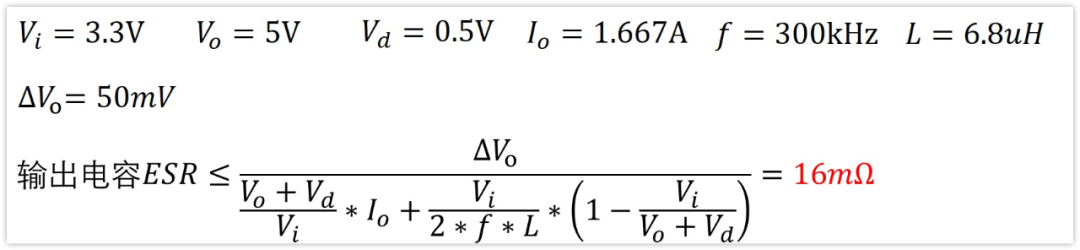
即輸出濾波電容的ESR如果控制在16mΩ,那么能將輸出紋波電壓控制在50mV
如果我們使用常規的Low ESR鋁電解電容,比如Leon的VZH系列
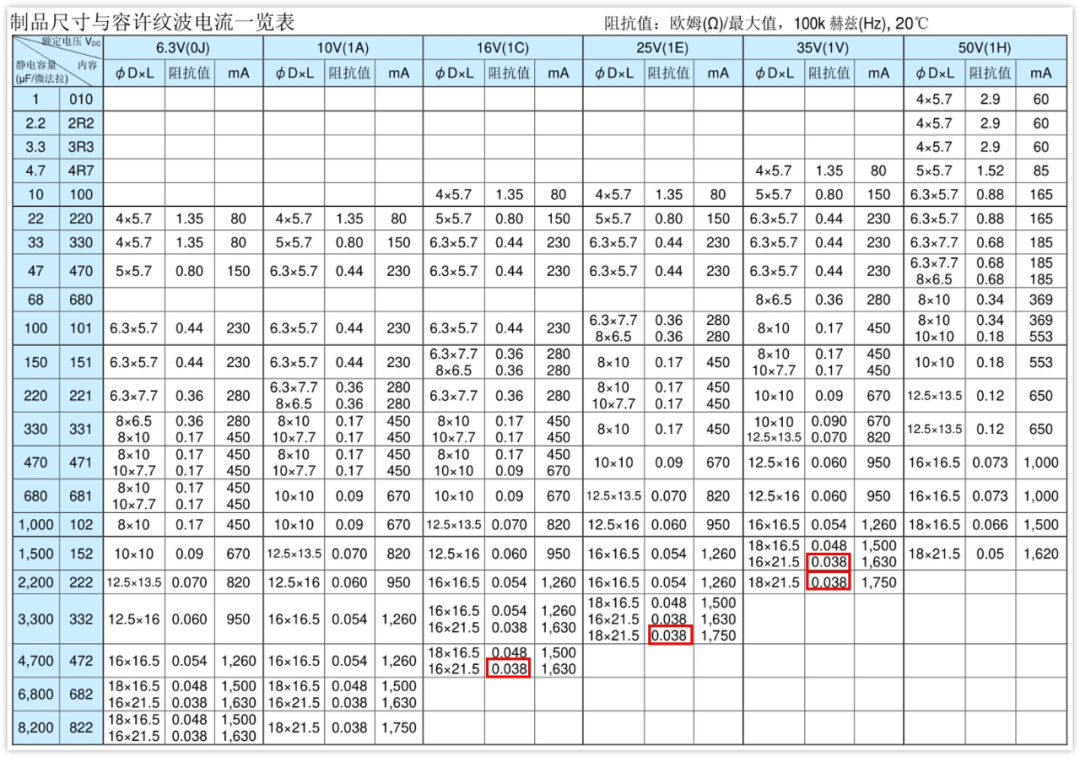
可以看到,滿足輸入46mΩ的電容容量非常大,都到了1500uF以上。滿足輸出16mΩ的濾波電容都沒有。
所以說,常規的鋁電解電容用在開關電源上面濾波,效果是比較差的,紋波很難控制得比較低。
不過,也有一種電容叫做固態鋁電解電容,已經是在廣泛使用的。
假定我們現在選用尼吉康的PCF系列鋁固態電解電容。
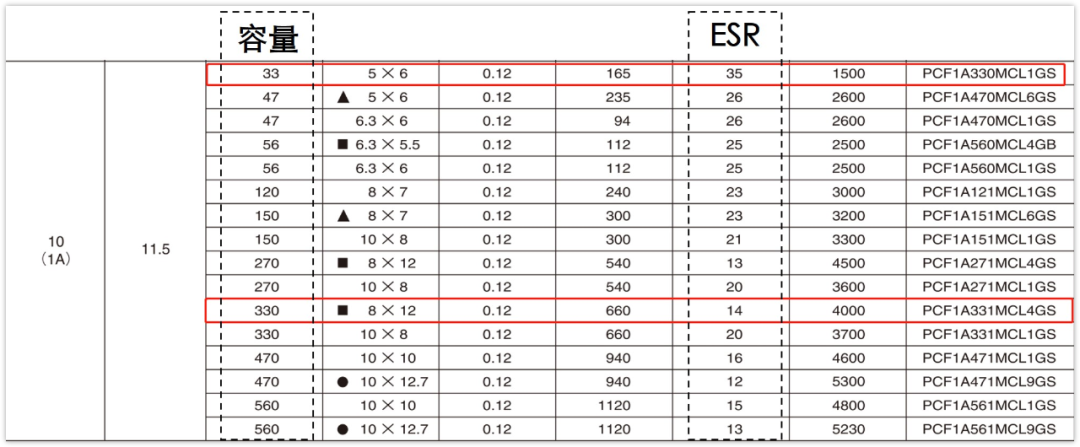
可以看到,33uF的可以大致是可以滿足輸入紋波要求,330uF大致是可以滿足輸出的紋波要求得。
從官網上面下載這330uF電容的spice文件(PCF1A331MCL4GS),接到輸出端濾波(輸入就不看了),同時加了2個100nF的電容,構建仿真電路圖。
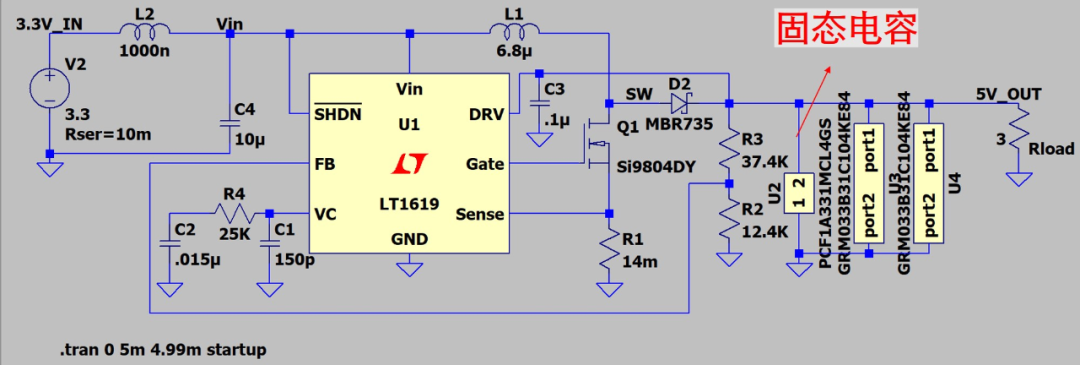
仿真結果如下:
可以看到,不算毛刺紋波不高,但是毛刺振蕩非常明顯,加了2個100nF濾波也只能控制在300mV左右。
現在討論不算毛刺的紋波也沒有意義了,因為去不掉,我們肯定是看總的輸出噪聲是300mV,這個有點大。
這個原因應該是固態電容的等效串聯電感太大,我比較了一下這個電容和前面的47uF陶瓷電容的spice文件,確實是固態電容的電感更大的。
所以,總的來說,不論是鋁電解電容,還是固態電容,都是沒有陶瓷電容好的,這也是為什么很多dcdc芯片手冊都推薦使用陶瓷電容濾波的原因吧。
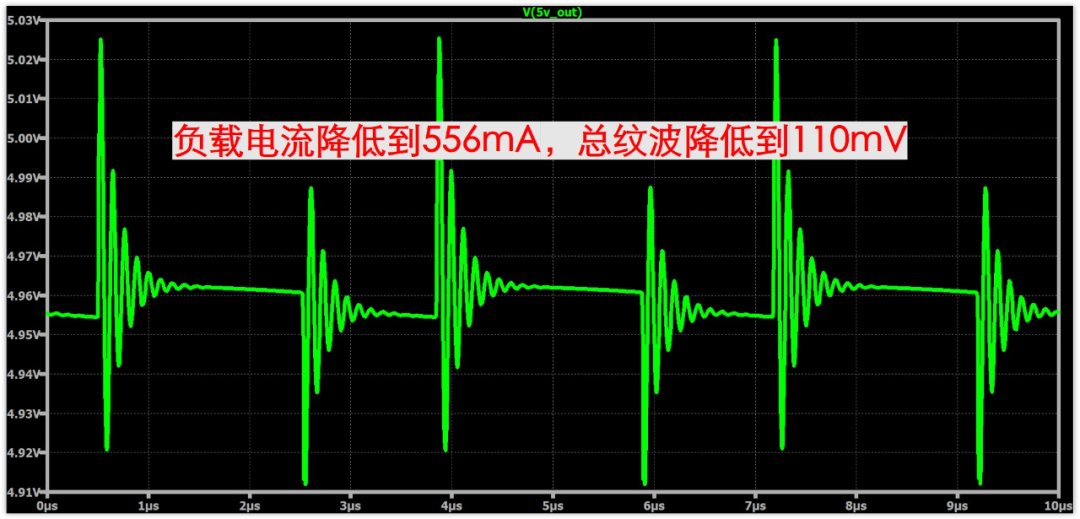
當然,也不是說鋁電解電容不能用,因為我舉的例子負載電流達到了1.667A的,這個算是比較大的,如果負載電流減小到三分之一,輸出紋波(包括毛刺振蕩)噪聲也降低了,如下圖,降低到了110mV左右,紋波要求不嚴格的話也可以用了。
這里有一個使用電解電容濾波,輸出振蕩很嚴重的例子,有興趣可以看看,我覺得他如果將鋁電解換成陶瓷電容濾波,可能會改善很多,鏈接如下:
https://bbs.21dianyuan.com/forum.php?mod=viewthread&tid=289717
小結
這文章字數破紀錄了,1w多,我也不想如此,只不過之前還是有同志們說有點難懂,我只能寫一句解釋一下,不好文字說明的地方就畫圖,圖片也60多張了吧,最后就這樣臭長臭長了。
所以總結的第1點就是:有點累。
第2點就是,推導公式確實可以加深對boost的理解,對各處的信號都能了如指掌,這對我們設計boost還是很有用的,特別是出現問題的時候,自然而然都能想到改怎么分析。
第3點就是,計算公式與真實值是有較大差距的
推導的公式,是基于boost的基本拓撲來的,這跟實際使用還是有較大的區別。
其中最大的一點就是,沒有公式來計算毛刺(高頻振蕩),而很多時候,毛刺占輸出波動最主要的部分。
所以公式僅僅只能作為參考,更重要的是,我們要對各種基本器件有一個較深的了解,比如我文章舉例的陶瓷電容,鋁電解電容,固態電容,這三種器件極大的影響了最終的結果,如果只是浮于表面,遇到問題只能東試試,西試試吧,能不能搞定就看運氣了。
審核編輯 :李倩
-
電路
+關注
關注
172文章
5962瀏覽量
172727 -
Boost
+關注
關注
5文章
370瀏覽量
48246 -
公式
+關注
關注
0文章
22瀏覽量
16059
原文標題:手撕Boost!Boost公式推導及驗證
文章出處:【微信號:mcu168,微信公眾號:硬件攻城獅】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
TCM控制雙向Buck/Boost變換器中高精度可變開關頻率ZVS調節的實用電流推導方法
EMC常見公式大全
探討Boost電路參數設計的要點
buck電路穩態電壓推導過程
boost電路占空比有沒有限制
級聯噪聲系數公式的推導
pfc電路和boost電路的區別
boost升壓電路原理和占空比的關系
BOOST升壓電源原理,含仿真文件

LTC3115在boost模式下的輸出不穩定如何解決?
boost電路頻率大小影響什么 boost電路輸入輸出電壓關系
Boost電路的工作原理及推導公式

boost電路工作原理 boost電路輸出電壓和輸入電壓的關系




 Boost公式推導及驗證
Boost公式推導及驗證










評論