鐵子們,我是小風哥,你也可以叫我島主
今天給大家帶來一道極其經典的題目,叫做最大和子數組,給定一個數組,找到其中的一個連續子數組,其和最大。
示例:
輸入:nums=[-2,1,-3,4,-1,2,1,-5,4]
輸出:6
解釋:子數組[4,-1,2,1]的和為6,其它任何連續的子數組和不超過6.
想一想該怎樣解決這個問題。
如果你一時想不到解法可以從暴利解法開始。
暴力求解
這種解法最簡單,我們把所有子數組找出來,然后依次計算其和,找出一個最大的出來,比如給定數組[1,2,3],那么我們能找出子數組:[1],[2],[3],[1,2],[2,3],[1,2,3],很顯然這里和最大的子數組為[1,2,3],其值為6。
intsum(vector&nums,intb,inte){
intres=0;
for(;b<=?e;?b++)?{
????????res?+=?nums[b];
????}
????returnres;
}
intmaxSubArray(vector&nums){
intsize=nums.size();
intres=0x80000000;
for(inti=0;ifor(intj=i;jreturnres;
}
這種解法最簡單,該算法的時間復雜度為O(n^3),其中找出所有子數組的時間復雜度為O(n^2),計算每個子數組的和的時間復雜度為O(n),因此其時間復雜度為O(n^3)。
讓我們再來看一下這個過程,這里的問題在于計算每個子數組的和時有很多重復計算,比如我們知道了子數組[1,2]的和后再計算數組[1,2,3]的值時完全可以利用子數組[1,2]的計算結果而無需從頭到尾再算一遍,也就是說我們可以利用上一步的計算結果,這本身就是動態規劃的思想。

基于該思想我們可以對上述代碼簡單改造一下:
intmaxSubArray(vector&nums){
intsize=nums.size();
intres=0x80000000;
for(inti=0;ifor(intj=i+1;jreturnres;
}
看到了吧,代碼不但更簡潔,而且運行速度更快,該算法的時間復雜度為O(n^2),比第一種解法高了很多。
還有沒有進一步提高的空間呢?
答案是肯定的。
分而治之
我們在之前的文章中說過,分治也是一種非常強大的思想,具體應該這里的話我們可以把整個數組一分為二,然后子數組也一分為二,不斷劃分下去就像這樣:
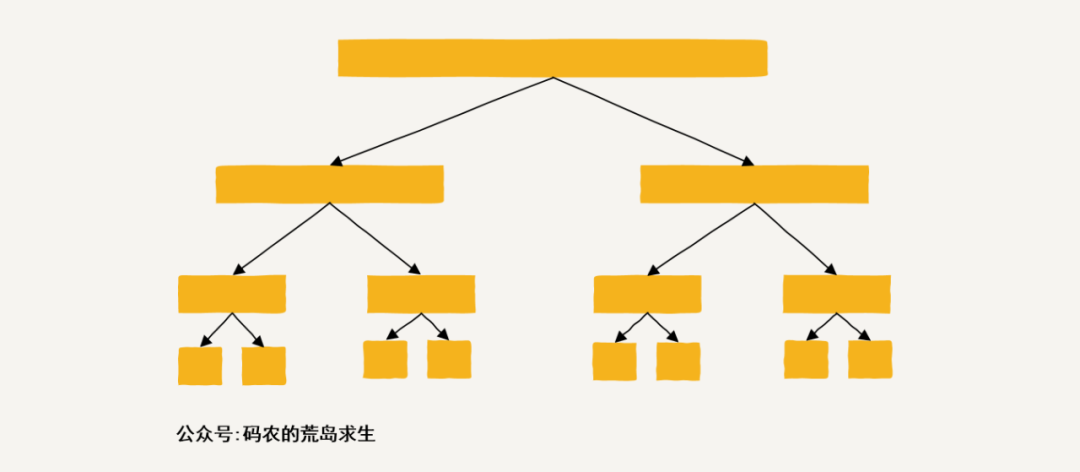
然后呢?
然后問題才真正開始有趣起來,注意,當我們劃分到最下層的時候,也就是不可再劃分時會得到兩個數組元素,比如對于數組[1,2]會劃分出[1]與[2],此時[1]與[2]不可再劃分,那么對于子問題[1,2],其最大子數組的和為max(1+2, 1,2),也就是說要么是左半部分的元素值、要么是右半部分的元素值、要么是兩個元素的和,就這樣我們得到了最后兩層的答案:
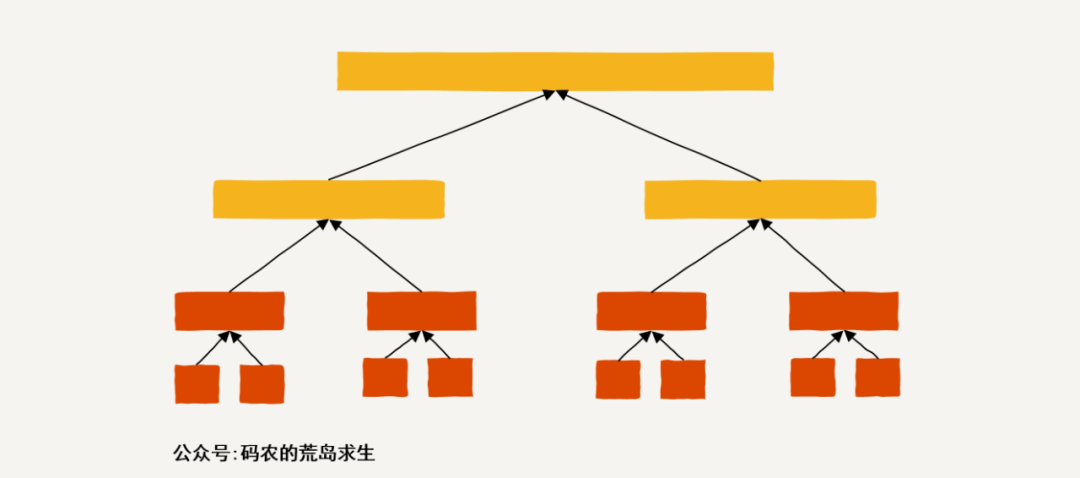
假設對于數組[1,2,3,4],一次劃分后得到了[1,2]與[3,4],用上面的方法我們可以分別知道這兩個問題的最大子數組和,我們怎樣利用上述的答案來解決更大的問題,也就是[1,2,3,4]呢?
很顯然,對于[1,2,3,4]來說,最大子數組的和要么來自左半部分、要么來自右半部分、要么來自中間部分——也就是包含2和3,其中左半部分和右半部分的答案我們有了,那么中間部分的最大和該是多少呢?
其實這個問題很簡單,我們從中間開始往兩邊不斷累加,然后記下這個過程的最大值,比如對于[1,-2,3,-4,5],我們從中間的3開始先往左邊累加和是:{1+(-2)+3, (-2)+3, 3}也就是{2,1,3},因此我們以中間數字為結尾的最大子數組和為3:
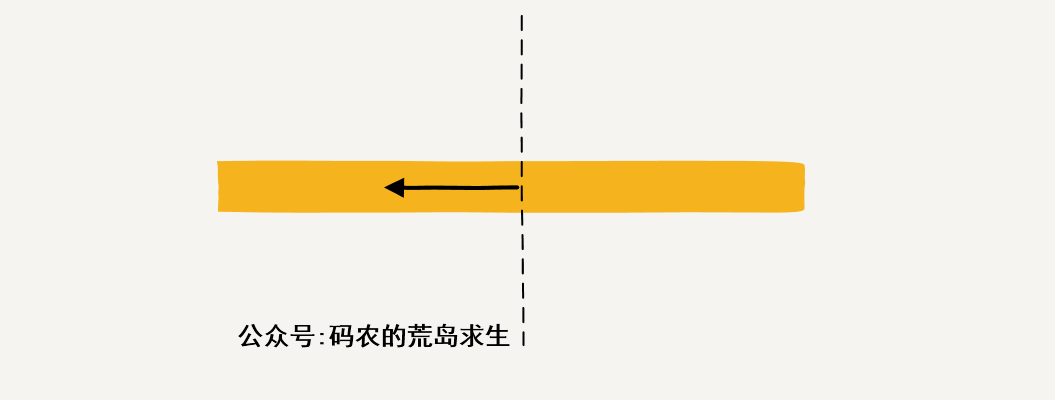
另一邊也是同樣的道理,只不過這次是以中間數字為起點向右累加:
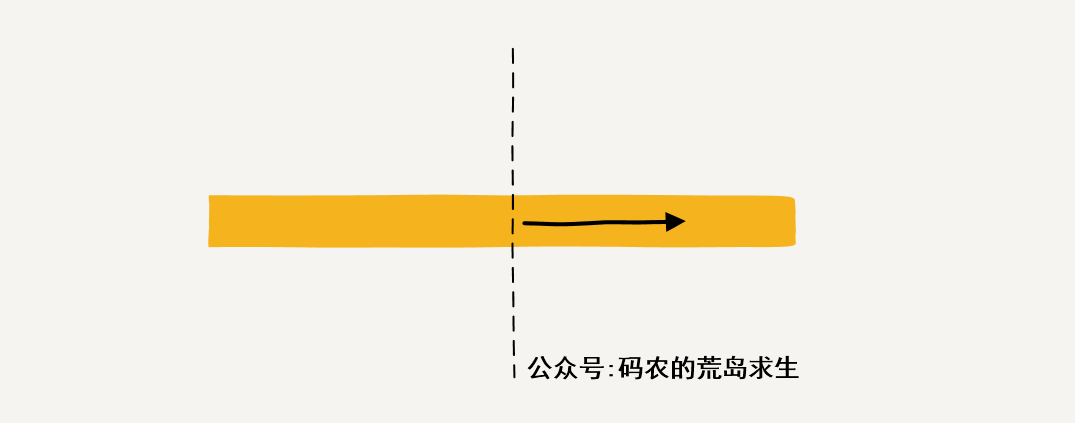
然后這三種情況中取一個最大值即可,這樣我們就基于子問題解決了更大的問題:
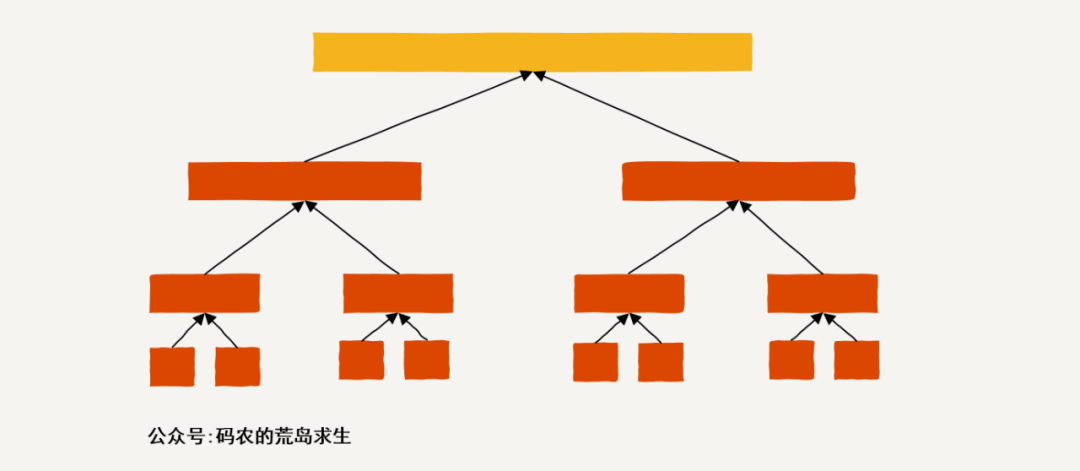
此后的道理一樣,最終我們得到了整個問題的解。
根據上面的分析就可以寫代碼了:
intgetMaxSum(vector&nums,intb,inte){
if(b==e)returnnums[b];
if(b==e-1)returnmax(nums[b],max(nums[e],nums[b]+nums[e]));
intm=(b+e)/2;
intmaxleft=nums[m];
intmaxright=nums[m];
intsum=nums[m];
for(inti=m+1;i<=?e;?i++)?{
????????sum?+=?nums[i];
????????maxright?=?max(maxright,?sum);
????}
????sum?=?nums[m];
????for(inti=m-1;i>=b;i--){
sum+=nums[i];
maxleft=max(maxleft,sum);
}
returnmax(getMaxSum(nums,b,m-1),max(getMaxSum(nums,m+1,e),maxleft+maxright-nums[m]));
}
intmaxSubArray(vector&nums){
returngetMaxSum(nums,0,nums.size()-1);
}
上述這段代碼的時間復雜度為O(NlogN)比第二種方法又提高了很多。
動態規劃
實際上這個問題還有另一種更妙的解決方法,我們令dp(i)表示以元素A[i]為結尾的最大子數組的和,那么根據這一定義則有:
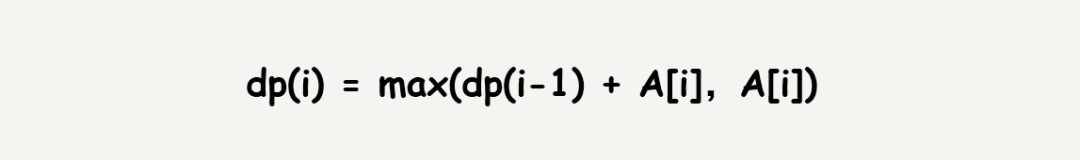
這是很顯然的,注意dp(i)的定義,是以元素A[i]為結尾的最大子數組的和,因此dp(i)的值要么就是A[i]連接上之前的一個子數組,那么不鏈接任何數組,那么最終的結果一定是以某個元素為結尾的子數組,因此我們從所有的dp(i)中取一個最大的就好了,依賴子問題解決當前問題的解就是所謂的動態規劃。
有了這些分析,代碼非常簡單:
intmaxSubArray(vector&nums){
intsize=nums.size();
vectordp(size,0);
intres=dp[0]=nums[0];
for(inti=1;ireturnres;
}
這段代碼簡單到讓人難以置信,只有8行代碼,你甚至可能會懷疑這段代碼的正確性,但它的確是沒有任何問題的,而且這段代碼的時間復雜度只有O(N),這段代碼既簡單運行速度又快,這大概就是算法的魅力吧。
審核編輯 :李倩
-
代碼
+關注
關注
30文章
4823瀏覽量
68897 -
數組
+關注
關注
1文章
417瀏覽量
26003
原文標題:動態規劃:8行代碼搞定最大子數組和問題
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
Labivew 實現鼠標在數組中選中元素時,精準的顯示所在位置的行、列值方法
數組的下標為什么可以是負數
數組名之間可以直接賦值嗎
指針數組和二維數組有沒有區別
labview按行讀取二維數組之后再按讀取順序重新組成二維數組如何實現?
labview字符串數組轉化為數值數組
面試常考+1:函數指針與指針函數、數組指針與指針數組





 動態規劃:8行代碼搞定最大子數組和問題
動態規劃:8行代碼搞定最大子數組和問題











評論