1.圖像銳化原理介紹
在增強圖像之前一般會先對圖像進行平滑處理以減少或消除噪聲。圖像的能量主要集中在低頻部分,而噪聲和圖像邊緣信息的能量主要集中在高頻部分。因此,平滑處理會使原始圖像的邊緣和輪廓變得模糊。為了減少這類不利效果的影響,需要利用圖像銳化技術,使圖像的邊緣變得清晰。圖像銳化處理主要有兩個目的:一是與圖像平滑處理相反,增強圖像邊緣,使模糊的圖像更加清晰,顏色變得鮮明突出,圖像的質量有所改善,產生更適合人觀察和識別的圖像;二是經過銳化處理后,目標物體的邊緣鮮明,以便于計算機提取目標物體的邊界、對圖像進行分割、目標區域識別、區域形狀提取等,為圖像理解和分析打下基礎。 經過平滑處理的圖像變得模糊的根本原因是因為圖像受到了平均或積分運算,因此可以對其進行逆運算(如微分運算)就可以使圖像變得清晰。微分運算是求信號的變化率,由傅立葉變換的微分性質可知,微分運算具有加強高頻分量的作用。但需要注意的是,進行銳化處理的圖像必須有較高的性噪比,否則銳化后圖像性噪比反而更低,從而使得噪聲增加的比信號還要多,因此一般是先消除或減輕噪聲后再進行銳化處理,如圖1所示。

圖1 圖像銳化示意圖
物體的邊緣是以圖像局部特性不連續性的形式出現的,即邊緣意味著一個區域的結束和另一個區域的開始。圖像邊緣有方向和幅度兩個參數。通常,沿邊緣走向的像素變化平緩,而垂直于邊緣走向的像素變化劇烈。邊緣一般有兩類(圖2所示):(1)階躍狀邊緣,它兩邊的像素灰度值顯著不同;(2)屋頂狀邊緣,它位于像素灰度值從增加到減少(或從減少到增加)的變化轉折點。經典的邊緣提取方法是考慮圖像的每個像素在某個領域內的變化,利用邊緣鄰近一階或二階方向導數變化規律來檢測邊緣。圖像灰度值的顯著變化可以用一階差分替代一階微分的梯度來表示,分別以梯度向量的幅度和方向來表示。因此,圖像中陡峭邊緣的梯度值很大;灰度值變化平緩的地方,梯度值較小;灰度值相同的地方,梯度值為零。
下面開始介紹運用一階微分和二階微分運算來進行圖像邊緣檢測的原理。
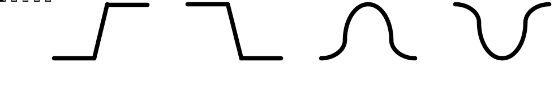
圖2 邊緣類型
1.1.一階微分邊緣檢測
一階微分主要是指梯度模運算,圖像的梯度模值包含了邊界及細節信息。圖像![]() 在點
在點![]() 處的梯度定義為:
處的梯度定義為:
由于數字圖像是離散的,所以可以用差分來替代微分,即:
梯度的幅值即模值,為:
梯度的方向為:
對圖像f使用梯度模算子進行運算后,可產生一幅梯度圖像g,圖像g和圖像f之間的像素關系為:
其中G為梯度模算子。由于梯度圖像g反映了圖像f的灰度變化分布信息,因此可以對其進行某種適當的處理和變換,或將變換后的梯度圖像和原圖像組合作為f銳化后的圖像。運用一階微分運算的邊緣檢測算子包括Robert算子、Prewitt算子和Sobel算子等等,將在后續小節中對Robert和Sobel邊緣檢測算法的實現進行介紹。
1.2.二階微分邊緣檢測
二階微分定義為![]() 。考慮坐標旋轉變換,設P點旋轉前坐標為
。考慮坐標旋轉變換,設P點旋轉前坐標為![]() ,順時針旋轉θ°后得
,順時針旋轉θ°后得![]() ,如圖3所示,則有:
,如圖3所示,則有:
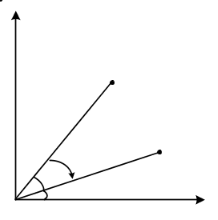
圖3 坐標旋轉變換
函數![]() 對
對![]() 的一階偏導數為
的一階偏導數為
函數![]() 對
對![]() 的一階偏導數為
的一階偏導數為
函數![]() 對
對![]() 的二階偏導數為
的二階偏導數為
函數![]() 對
對![]() 的二階偏導數為
的二階偏導數為
將函數![]() 對
對![]() 和
和![]() 的二階偏導數相加得
的二階偏導數相加得
后續小節將要介紹的Laplacian邊緣檢測算法正是基于二階微分運算。
由此可見,二階微分具有各向同性、旋轉不變性的特征,從而滿足不同走向的圖像邊緣的銳化要求。由于數字圖像是離散的,所以可以用差分來替代微分,即:
后續小節將要介紹的Laplacian邊緣檢測算法正是基于二階微分運算。
1.3.一階微分與二階微分邊緣檢測對比
一階微分和二階微分運算都可以用來檢測圖像邊緣,但它們對邊緣的檢測原理和檢測效果是有差異的,如下所示:(1)對于突變型的細節,通過一階微分的極值點和二階微分的過零點均可以檢測出來,如圖4所示。
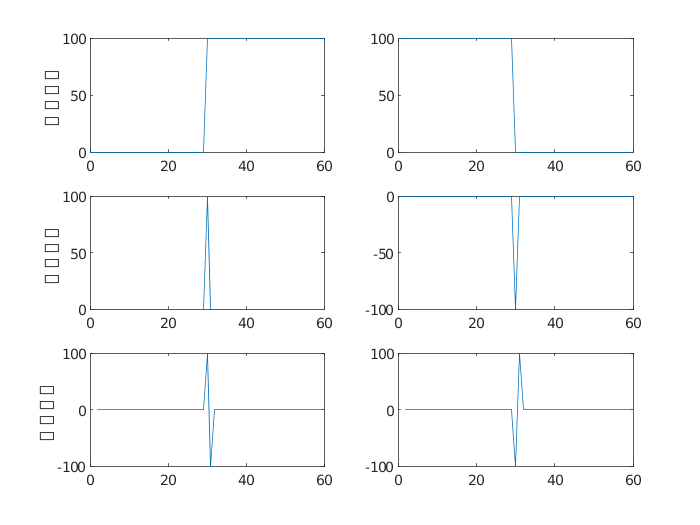
圖4 突變型細節
(2)對于細線型的細節,通過一階微分的過零點和二階微分的極值點均可以檢測出來,如圖5所示。
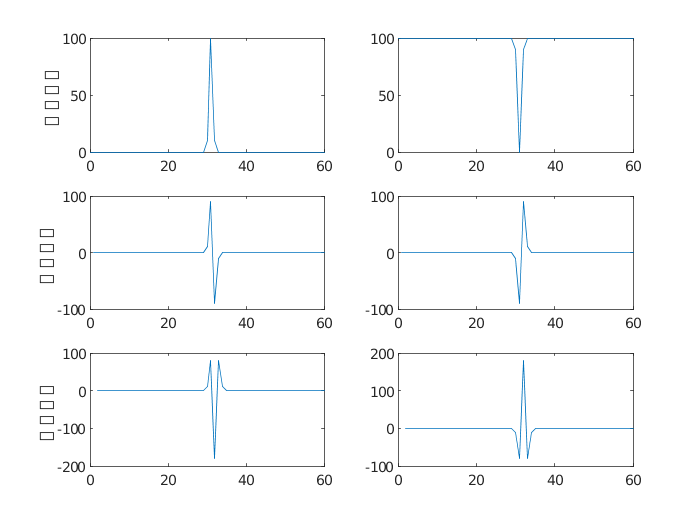
圖5 細線型細節
(3)對于漸變型的細節,一般情況下突變幅度小、定位難、不易檢測,但二階微分的信息比一階微分的信息多,如圖6所示。
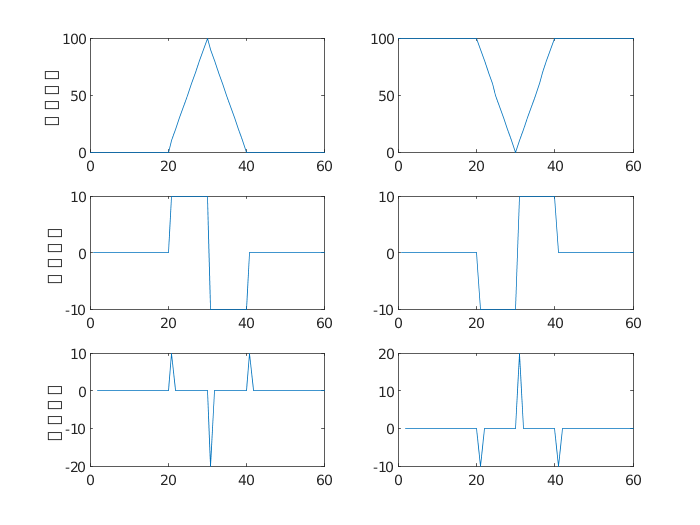
圖6 漸變型細節
從圖像的景物細節的灰度分布特性可知,有些灰度變化特性一階微分的描述不是很明確,為此,采用二階微分能夠獲得更豐富的景物細節。
2.Sobel邊緣檢測與銳化的實現
2.1.Sobel邊緣檢測算法理論
Robert算子只采用梯度微分銳化圖像,會讓噪聲、條紋得到增強,而Sobel邊緣檢測算子則在一定程度上解決了這個問題,它是一種先求平均、再求微分、最后求梯度的算子,其算子形式如下所示。顯然,Sobel算子只考慮了源像素點周圍8個相鄰像素點的水平和垂直方向的像素突變,而沒有加入源像素點灰度值的計算。
Sobel算子的水平和垂直模板如圖12所示,分別對水平邊緣和垂直邊緣的影響最大。
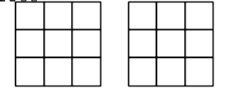
圖12 Sobel算子模板
Sobel算子在一個方向求微分,而在另一個方向求平均,因而對噪聲相對不敏感,具有抑制噪聲的作用。由于像素平均相當于對圖像進行低通濾波,所以Sobel算子對邊緣的定位不如Robert算子。但與Robert算子相比,Sobel算子有一定的抗干擾性,圖像效果比較干凈。
利用算子模板可求得水平和垂直方向的梯度![]() 和
和![]() ,再通過梯度合成便可獲得邊緣檢測結果
,再通過梯度合成便可獲得邊緣檢測結果![]() ,如下所示:
,如下所示:
有時,為了簡化運算,可以用下面式子來近似替代。
Sobel邊緣檢測的過程如圖13所示,獲得了比較粗的邊界,但邊緣定位精度不夠高,,有時可能對非邊緣像素的響應大于某些邊緣處的響應或者響應差別不是很大,造成漏檢或誤檢。當對精度要求不是很高時,是一種較為常用的邊緣檢測方法。將邊緣檢測結果與原圖疊加便可以得到銳化后的圖像,如圖14所示。
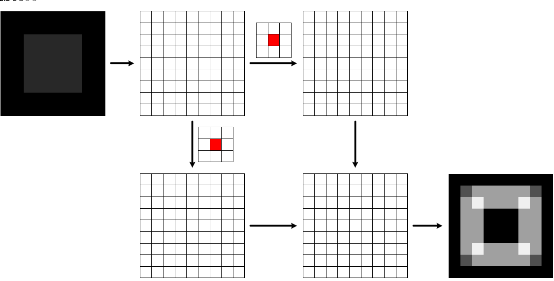
圖13 Sobel邊緣檢測

圖14 Sobel銳化
2.2.Sobel邊緣檢測Matlab實現
前面已經對Sobel邊緣檢測算法進行了介紹,現在基于Matlab軟件對其進行仿真。創建函數Sobel_Edge_Detector用于實現Sobel算子對圖像進行邊緣檢測,相關的matlab代碼如下所示(詳見Sobel_Edge_Detector.m)。
% 灰度圖像Sobel邊緣檢測算法實現
% IMG為輸入的灰度圖像
% Q為輸出的灰度圖像
function Q = Sobel_Edge_Detector(IMG)
[h,w] = size(IMG);% 獲取圖像的高度h和寬度w
Q = zeros(h,w);% 初始化Q為全0的h*w大小的圖像
% -------------------------------------------------------------------------
%WxWyPixel
% [-1-2-1][+10-1][P1P2P3]
% [000][+20-2][P4P5P6]
% [+1+2+1][+10-1][P7P8P9]
Wx = [-1,-2,-1;0,0,0;1,2,1];% Weight x
Wy = [1,0,-1;2,0,-2;1,0,-1];% Weight y
IMG = double(IMG);
for i = 1 : h
forj = 1 : w
if(i<2|| i>h-1 || j<2 || j>w-1)
Q(i,j)= 0;% 邊緣像素不處理
else
%Gx = sum(Wx.*IMG(i-1:i+1,j-1:j+1),'all');
Gx= Wx(1,1)*IMG(i-1,j-1) + Wx(1,2)*IMG(i-1,j) + Wx(1,3)*IMG(i-1,j+1) +...
Wx(2,1)*IMG(i,j-1)+ Wx(2,2)*IMG(i,j) + Wx(2,3)*IMG(i,j+1) +...
Wx(3,1)*IMG(i+1,j-1)+ Wx(3,2)*IMG(i+1,j) + Wx(3,3)*IMG(i+1,j+1);
%Gy = sum(Wy.*IMG(i-1:i+1,j-1:j+1),'all');
Gy= Wy(1,1)*IMG(i-1,j-1) + Wy(1,2)*IMG(i-1,j) + Wy(1,3)*IMG(i-1,j+1) +...
Wy(2,1)*IMG(i,j-1)+ Wy(2,2)*IMG(i,j) + Wy(2,3)*IMG(i,j+1) +...
Wy(3,1)*IMG(i+1,j-1)+ Wy(3,2)*IMG(i+1,j) + Wy(3,3)*IMG(i+1,j+1);
%Q(i,j) = sqrt(Gx^2 + Gy^2);
Q(i,j)= abs(Gx) + abs(Gy);
end
end
end
Q=uint8(Q);
上述Matlab代碼中需要注意以下幾點:
(1)函數輸入IMG是uint8數據類型的圖像,而計算時存在負數和小數,需要用浮點數來表示,所以將IMG由uint8數據類型轉為double數據類型;
(2)對圖像邊緣的像素不進行處理,直接輸出0;
(3)將函數輸出Q由double數據類型轉為uint8數據類型。
接下來編寫頂層M文件,相關的Maltab代碼如下所示(詳見Sobel_Sharpen_Test.m),Sobel銳化處理流程如圖15所示。
clear all;
close all;
clc;
% -------------------------------------------------------------------------
% Read PC image to Matlab
IMG1 = imread('../../0_images/Lenna.jpg');% 讀取jpg圖像
IMG1 = rgb2gray(IMG1);
subplot(131);imshow(IMG1);title('【1】原圖');
% -------------------------------------------------------------------------
IMG2 = Sobel_Edge_Detector(IMG1);
subplot(132);imshow(IMG2);title('【2】Sobel邊緣檢測結果');
% -------------------------------------------------------------------------
IMG3 = IMG1 + IMG2;
subplot(133);imshow(IMG3);title('【3】Sobel銳化圖像');
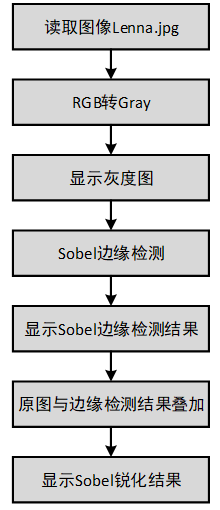
圖15 Sobel銳化處理流程
執行頂層M文件可得到圖16所示的結果,其中【2】是進行Sobel邊緣檢測得到的效果圖,可以看出Sobel算子對邊緣有較強的響應,與Robert算子相比,對邊緣的響應更加強烈,得到的邊緣更加寬;【3】是原圖與邊緣檢測結果疊加后的效果圖,相比原圖,邊緣和細節更加突出,但圖像有些失真。

圖16 Sobel邊緣檢測與銳化
原文標題:常用銳化算法及Sobel銳化的介紹
文章出處:【微信公眾號:機器視覺智能檢測】歡迎添加關注!文章轉載請注明出處。
審核編輯:湯梓紅
-
算法
+關注
關注
23文章
4622瀏覽量
93057 -
圖像
+關注
關注
2文章
1087瀏覽量
40501 -
檢測
+關注
關注
5文章
4498瀏覽量
91556
原文標題:常用銳化算法及Sobel銳化的介紹
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 Sobel邊緣檢測與銳化的實現
Sobel邊緣檢測與銳化的實現


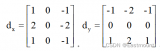










評論