本文介紹了使用 go 實現紅黑樹。

二叉搜索樹（二叉查找樹）

二叉查找樹也叫二叉搜索樹，也叫二叉排序樹，它具有以下特點：1. 如果左子樹不為空，則左子樹上的結點的值都小于根節點；2. 如果右子樹不為空，則右子樹上的結點的值都大于根節點；3. 子樹同樣也要遵循以上兩點。

二叉樹的遍歷方式

二叉樹的遍歷方式：前序遍歷、中序遍歷、后序遍歷和層序遍歷（MySql）。

只要一棵樹是二叉查找樹，那么它的中序遍歷（左根右輸出）一定是有序的。比如看下邊的一棵二叉樹：

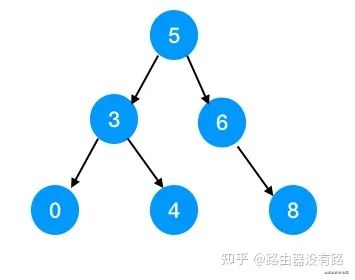
它的前序遍歷（根左右）為：530468；
它的中序遍歷（左根右）為：034568；
它的后序遍歷（左右根）為：043865。

二叉搜索樹有哪些應用？

既然是搜索樹，那么它肯定就是用在查找上。我們來分析下它的查找時間復雜度：

先來看下面兩顆二叉搜索樹：

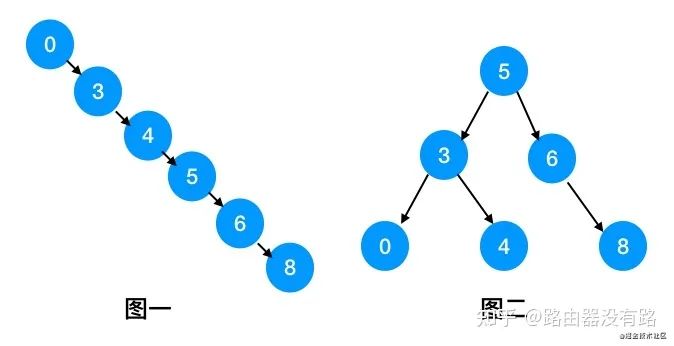
查找時間復雜度其實就是樹的深度。

上圖一的時間復雜度：O(n)時間復雜度，表示需要查找 n 次，即循環 n 遍，退化成鏈表的情況。

上圖二的時間復雜度（類似二分查找）：logn，即 => x= => logn。

那么為什么會出現退化成鏈表的情況（圖一）呢？我們該怎么處理才不會變成鏈表呢（怎么解決）？

當插入的節點數值從小到大時，則就會出現二叉樹退化成鏈表的情況，那么有另一種樹可以解決這種情況，就是平衡二叉樹（AVL樹）。

AVL樹是一種追求極致平衡的二叉搜索樹，即將樹調整到最優的情況，由于這種樹結構比較苛刻、旋轉也比較多，這里就不重點展開講。

紅黑樹

紅黑樹的由來

今天需要重點講的是紅黑樹。紅黑樹的底層數據結構其實就是二叉查找樹，也就是說紅黑樹是一顆特殊的二叉查找樹，也叫自平衡二叉查找樹。

紅黑樹出現的目的就是上所講到的，為了解決二叉樹退化成鏈表的情況。

紅黑樹的演進過程

鏈表(暴力查處) -> 二叉樹 -> 二叉查找樹 -> 特殊的二叉查找樹(自平衡的二叉查找樹)

紅黑色講解

通過上面的例子以及兩個圖，我們發現二叉樹的結構就決定了其搜索的效率及性能，那么我們需要怎么樣才讓二叉樹達到優化的效果呢？

因此就有了紅黑樹了，我們看下圖（紅黑樹）：

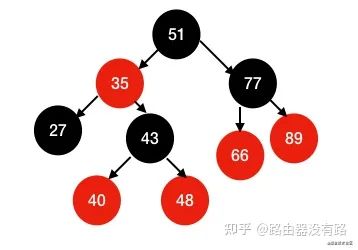
紅黑樹的性質：

每個節點不是紅色就是黑色（這里不一定要紅色和黑色，只要知道這里的紅色和黑色是什么意思即可）

一定沒有連在一起的紅色節點

根節點（第一個節點）是黑色 root

每個紅色節點的兩個字節點都是黑色

葉子結點都是黑色（上圖中其實還有為null的葉子結點沒有畫出來），如下圖所示：

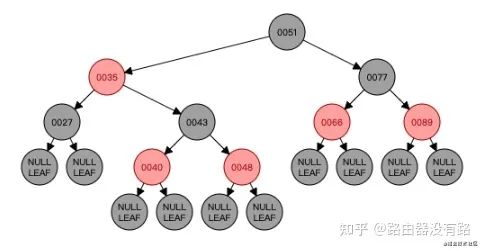
根據以上性質或者說滿足了以上性質的樹，就可以達到近似平衡了。

怎么判斷一個節點是否為根結點？

沒有父節點

入度為0的節點

紅黑樹變換規則

要滿足這些性質，需要對樹做什么操作呢？

為了紅黑可以滿足這些性質，因此出現了旋轉，那么紅黑樹有幾種變換規則呢？

有三種變換規則：

變色：紅變黑 黑變紅

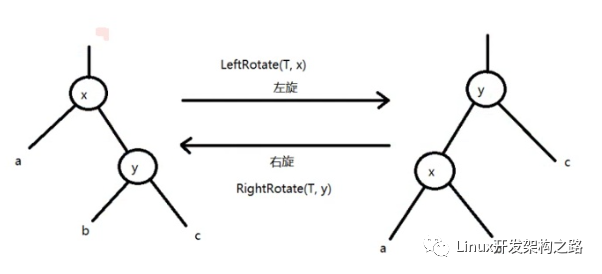
左旋轉

右旋轉

左旋轉示例：

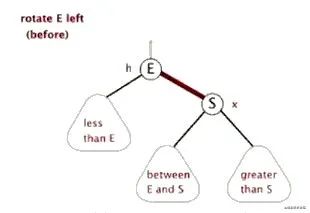
旋轉和顏色變換規則：所有插入的點默認為紅色； 1. 變顏色的情況：如果插入的節點的父節點和叔叔節點為紅色，則：1）把父節點和叔叔節點設為黑色；2）把爺爺(祖父)節點設為紅色；3）把指針定位到爺爺節點作為當前需要操作的節點，再根據變換規則來進行判斷操作。2. 左旋：如果當前父節點是紅色，叔叔節點是黑色，而且當前的節點是右子樹時，則需要以父節點作為左旋轉。3. 右旋：當前父節點是紅色，叔叔節點是黑色，且當前的節點是左子樹時，則：1）把父節點變為黑色；2）把爺爺節點變為紅色；3）以父節點右旋轉。

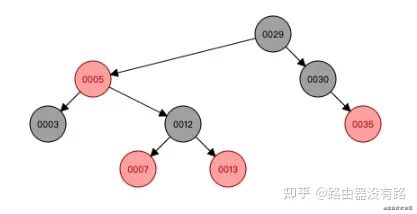
比如要往上圖中插入數字6，則這顆紅黑色的演變過程如下：

step1: 插入6節點后如下圖，它的父節點和叔叔節點均是紅色，則需要根據變換規則來操作，到step2了。

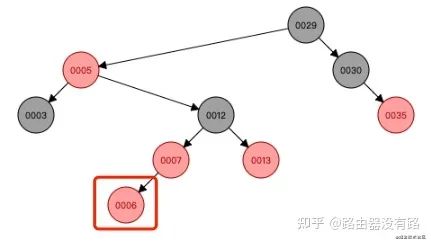
step2: 根據變換規則，需要將插入節點的父節點和叔叔節點均變為黑色，爺爺節點變為紅色，然后將指針定位到爺爺節點(藍色圈)。將指針定位到爺爺節點(12)后，此時做為當前需要操作的節點，再根據變換規則來判斷，可以看到下圖的當前節點(12)的叔叔節點是黑色的，則不能用變顏色規則的情況了，進行step3，此時需要進行左旋或右旋了。

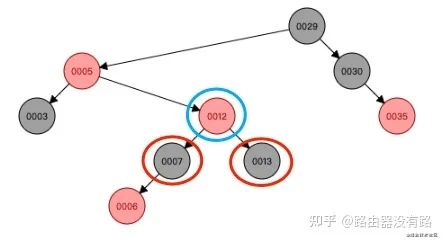
step3: 根據上圖情況可以知道此時是符合左旋規則的：當前節點(12)的父節點(5)是紅色，叔叔節點(3)是黑色，而且當前的節點是右子樹。接下來需要進行左旋變換(三步走)：

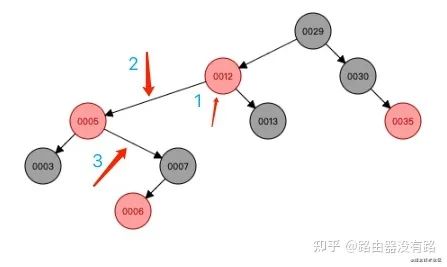
step4：左旋變換后，可以看到當前節點(5)的父節點(12)為紅色，叔叔節點(30)為黑色，而且當前節點為左子樹，符合右旋的規則。接下來就是進行右旋的變換操作了：1）把父節點(12)變為黑色；2）把爺爺節點(29)變為紅色；3）以父節點(12)右旋轉

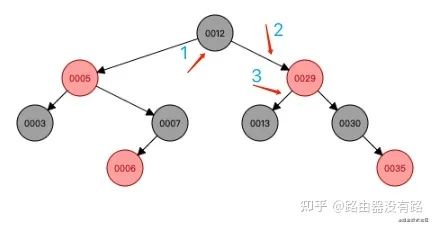
小結

到這里，可以看到經過多次旋轉后，這棵樹是符合紅黑色的性質。

Golang代碼實現紅黑樹

直接上代碼，如下：

packagemain

import(
"fmt"
"math/rand"
"time"
)

const(
REDbool=true
BLACKbool=false
)

typeNodestruct{
keyint
valueinterface{}

left*Node
right*Node
//parent*Node

colorbool
}

typeRedBlackTreestruct{
sizeint
root*Node
}

funcNewNode(key,valint)*Node{
//默認添加紅節點
return&Node{
key:key,
value:val,
left:nil,
right:nil,
//parent:nil,
color:RED,
}
}

funcNewRedBlackTree()*RedBlackTree{
return&RedBlackTree{}
}

func(n*Node)IsRed()bool{
ifn==nil{
returnBLACK
}
returnn.color
}

func(tree*RedBlackTree)GetTreeSize()int{
returntree.size
}

//nodex
///左旋轉/
//T1x--------->nodeT3
////
//T2T3T1T2
func(n*Node)leftRotate()*Node{
//左旋轉
retNode:=n.right
n.right=retNode.left

retNode.left=n
retNode.color=n.color
n.color=RED

returnretNode
}

//nodex
///右旋轉/
//xT2------->ynode
////
//yT1T1T2
func(n*Node)rightRotate()*Node{
//右旋轉
retNode:=n.left
n.left=retNode.right

retNode.right=n
retNode.color=n.color
n.color=RED

returnretNode
}

//顏色變換
func(n*Node)flipColors(){
n.color=RED
n.left.color=BLACK
n.right.color=BLACK
}

//維護紅黑樹
func(n*Node)updateRedBlackTree(isAddint)*Node{
//isAdd=0說明沒有新節點，無需維護
ifisAdd==0{
returnn
}

//需要維護
ifn.right.IsRed()==RED&&n.left.IsRed()!=RED{
n=n.leftRotate()
}

//判斷是否為情形3，是需要右旋轉
ifn.left.IsRed()==RED&&n.left.left.IsRed()==RED{
n=n.rightRotate()
}

//判斷是否為情形4，是需要顏色翻轉
ifn.left.IsRed()==RED&&n.right.IsRed()==RED{
n.flipColors()
}

returnn
}

//遞歸寫法:向樹的root節點中插入key,val
//返回1,代表加了節點
//返回0,代表沒有添加新節點,只更新key對應的value值
func(n*Node)add(key,valint)(int,*Node){
ifn==nil{//默認插入紅色節點
return1,NewNode(key,val)
}

isAdd:=0
ifkeyn.key{
isAdd,n.right=n.right.add(key,val)
}else{
//對value值更新,節點數量不增加,isAdd=0
n.value=val
}

//維護紅黑樹
n=n.updateRedBlackTree(isAdd)

returnisAdd,n
}

func(tree*RedBlackTree)Add(key,valint){
isAdd,nd:=tree.root.add(key,val)
tree.size+=isAdd
tree.root=nd
tree.root.color=BLACK//根節點為黑色節點
}

//前序遍歷打印出key,val,color
func(tree*RedBlackTree)PrintPreOrder(){
resp:=make([][]interface{},0)
tree.root.printPreOrder(&resp)
fmt.Println(resp)
}

func(n*Node)printPreOrder(resp*[][]interface{}){
ifn==nil{
return
}
*resp=append(*resp,[]interface{}{n.key,n.value,n.color})
n.left.printPreOrder(resp)
n.right.printPreOrder(resp)
}


//測試紅黑樹代碼
funcmain(){
count:=10
redBlackTree:=NewRedBlackTree()
nums:=make([]int,0)
fori:=0;i

	

	測試輸出結果如下：

	
datasource:[1779185060]
redBlackTree:-2.136μs
[[77false][11true][00false][66false][55true][99false][88true]]
節點數量:7


	

	總結

	紅黑樹是保持近似平衡的二叉樹，從另一種角度上來說紅黑樹不是平衡二叉樹，它的最大高度為2*logn。

	二分搜索樹，AVL樹，紅黑樹對比：1. 對于完全隨機的數據源，普通二分搜索樹很好用，缺陷是在極端情況下容易退化成鏈表 2. 對于查詢較多的使用情況，AVL樹很好用，因為他的高度一直保持h=logn 3. 紅黑樹犧牲了平衡性，即h=2*logn，但在添加和刪除操作中，紅黑樹比AVL樹有優勢 4. 綜合增刪改查所有操作，紅黑樹的統計性能更優

	原文標題：二叉樹、紅黑樹以及Golang實現紅黑樹

	文章出處：【微信公眾號：Linux愛好者】歡迎添加關注！文章轉載請注明出處。

	審核編輯：彭菁