讀完本文,可以去力扣解決如下題目:
1135. 最低成本聯(lián)通所有城市(中等)1584. 連接所有點(diǎn)的最小費(fèi)用(中等)本文是第 7 篇圖論算法文章,先列舉一下我之前寫(xiě)過(guò)的圖論算法:
2、二分圖判定算法
3、環(huán)檢測(cè)和拓?fù)渑判蛩惴?/span>
像圖論算法這種高級(jí)算法雖然不算難,但是閱讀量普遍比較低,我本來(lái)是不想寫(xiě) Prim 算法的,但考慮到算法知識(shí)結(jié)構(gòu)的完整性,我還是想把 Prim 算法的坑填上,這樣所有經(jīng)典的圖論算法就基本完善了。
Prim 算法和 Kruskal 算法都是經(jīng)典的最小生成樹(shù)算法,閱讀本文之前,希望你讀過(guò)前文Kruskal 最小生成樹(shù)算法,了解最小生成樹(shù)的基本定義以及 Kruskal 算法的基本原理,這樣就能很容易理解 Prim 算法邏輯了。
對(duì)比 Kruskal 算法
圖論的最小生成樹(shù)問(wèn)題,就是讓你從圖中找若干邊形成一個(gè)邊的集合mst,這些邊有以下特性:
1、這些邊組成的是一棵樹(shù)(樹(shù)和圖的區(qū)別在于不能包含環(huán))。
2、這些邊形成的樹(shù)要包含所有節(jié)點(diǎn)。
3、這些邊的權(quán)重之和要盡可能小。
那么 Kruskal 算法是使用什么邏輯滿足上述條件,計(jì)算最小生成樹(shù)的呢?
首先,Kruskal 算法用到了貪心思想,來(lái)滿足權(quán)重之和盡可能小的問(wèn)題:
先對(duì)所有邊按照權(quán)重從小到大排序,從權(quán)重最小的邊開(kāi)始,選擇合適的邊加入mst集合,這樣挑出來(lái)的邊組成的樹(shù)就是權(quán)重和最小的。
其次,Kruskal 算法用到了Union-Find 并查集算法,來(lái)保證挑選出來(lái)的這些邊組成的一定是一棵「樹(shù)」,而不會(huì)包含環(huán)或者形成一片「森林」:
如果一條邊的兩個(gè)節(jié)點(diǎn)已經(jīng)是連通的,則這條邊會(huì)使樹(shù)中出現(xiàn)環(huán);如果最后的連通分量總數(shù)大于 1,則說(shuō)明形成的是「森林」而不是一棵「樹(shù)」。
那么,本文的主角 Prim 算法是使用什么邏輯來(lái)計(jì)算最小生成樹(shù)的呢?
首先,Prim 算法也使用貪心思想來(lái)讓生成樹(shù)的權(quán)重盡可能小,也就是「切分定理」,這個(gè)后文會(huì)詳細(xì)解釋。
其次,Prim 算法使用BFS 算法思想和visited布爾數(shù)組避免成環(huán),來(lái)保證選出來(lái)的邊最終形成的一定是一棵樹(shù)。
Prim 算法不需要事先對(duì)所有邊排序,而是利用優(yōu)先級(jí)隊(duì)列動(dòng)態(tài)實(shí)現(xiàn)排序的效果,所以我覺(jué)得 Prim 算法類(lèi)似于 Kruskal 的動(dòng)態(tài)過(guò)程。
下面介紹一下 Prim 算法的核心原理:切分定理
切分定理
「切分」這個(gè)術(shù)語(yǔ)其實(shí)很好理解,就是將一幅圖分為兩個(gè)不重疊且非空的節(jié)點(diǎn)集合:
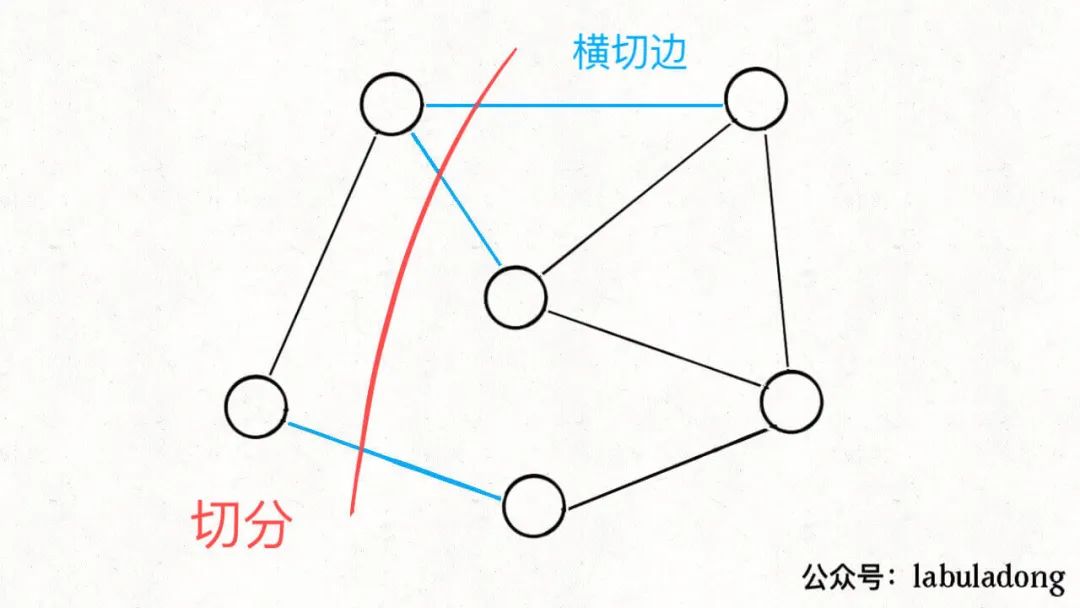
紅色的這一刀把圖中的節(jié)點(diǎn)分成了兩個(gè)集合,就是一種「切分」,其中被紅線切中的的邊(標(biāo)記為藍(lán)色)叫做「橫切邊」。
PS:記住這兩個(gè)專業(yè)術(shù)語(yǔ)的意思,后面我們會(huì)頻繁使用這兩個(gè)詞,別搞混了。
當(dāng)然,一幅圖肯定可以有若干種切分,因?yàn)楦鶕?jù)切分的定義,只要你能一刀把節(jié)點(diǎn)分成兩部分就行。
接下來(lái)我們引入「切分定理」:
對(duì)于任意一種「切分」,其中權(quán)重最小的那條「橫切邊」一定是構(gòu)成最小生成樹(shù)的一條邊。
這應(yīng)該很容易證明,如果一幅加權(quán)無(wú)向圖存在最小生成樹(shù),假設(shè)下圖中用綠色標(biāo)出來(lái)的邊就是最小生成樹(shù):
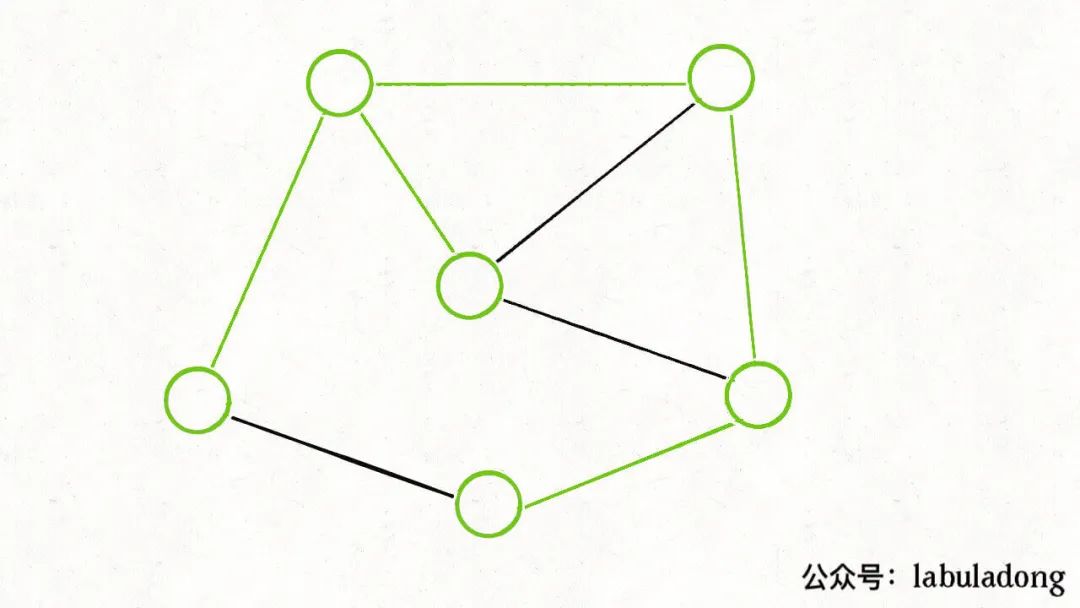
那么,你肯定可以找到若干「切分」方式,將這棵最小生成樹(shù)切成兩棵子樹(shù)。比如下面這種切分:
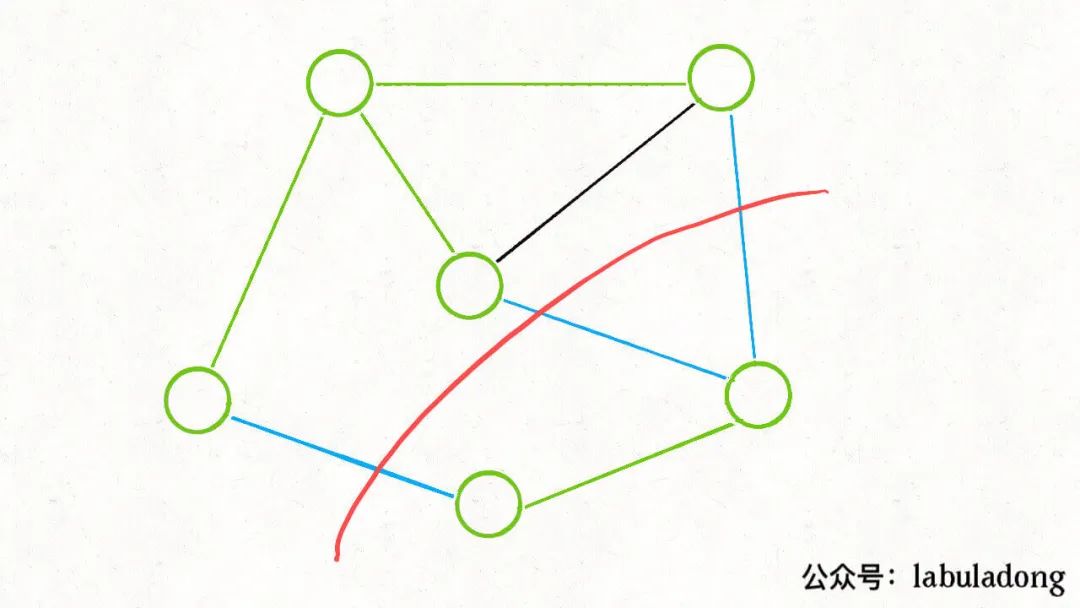
你會(huì)發(fā)現(xiàn),任選一條藍(lán)色的「橫切邊」都可以將這兩棵子樹(shù)連接起來(lái),構(gòu)成一棵生成樹(shù)。
那么為了讓最終這棵生成樹(shù)的權(quán)重和最小,你說(shuō)你要怎么選?
肯定選權(quán)重最小的那條「橫切邊」對(duì)吧,這就證明了切分定理。
關(guān)于切分定理,你也可以用反證法證明:
給定一幅圖的最小生成樹(shù),那么隨便給一種「切分」,一定至少有一條「橫切邊」屬于最小生成樹(shù)。
假設(shè)這條「橫切邊」不是權(quán)重最小的,那說(shuō)明最小生成樹(shù)的權(quán)重和就還有再減小的余地,那這就矛盾了,最小生成樹(shù)的權(quán)重和本來(lái)就是最小的,怎么再減?所以切分定理是正確的。
有了這個(gè)切分定理,你大概就有了一個(gè)計(jì)算最小生成樹(shù)的算法思路了:
既然每一次「切分」一定可以找到最小生成樹(shù)中的一條邊,那我就隨便切唄,每次都把權(quán)重最小的「橫切邊」拿出來(lái)加入最小生成樹(shù),直到把構(gòu)成最小生成樹(shù)的所有邊都切出來(lái)為止。
嗯,可以說(shuō)這就是 Prim 算法的核心思路,不過(guò)具體實(shí)現(xiàn)起來(lái),還是要有些技巧的。
因?yàn)槟銢](méi)辦法讓計(jì)算機(jī)理解什么叫「隨便切」,所以應(yīng)該設(shè)計(jì)機(jī)械化的規(guī)則和章法來(lái)調(diào)教你的算法,并盡量減少無(wú)用功。
Prim 算法實(shí)現(xiàn)
我們思考算法問(wèn)題時(shí),如果問(wèn)題的一般情況不好解決,可以從比較簡(jiǎn)單的特殊情況入手,Prim 算法就是使用的這種思路。
按照「切分」的定義,只要把圖中的節(jié)點(diǎn)切成兩個(gè)不重疊且非空的節(jié)點(diǎn)集合即可算作一個(gè)合法的「切分」,那么我只切出來(lái)一個(gè)節(jié)點(diǎn),是不是也算是一個(gè)合法的「切分」?
是的,這是最簡(jiǎn)單的「切分」,而且「橫切邊」也很好確定,就是這個(gè)節(jié)點(diǎn)的邊。
那我們就隨便選一個(gè)點(diǎn),假設(shè)就從A點(diǎn)開(kāi)始切分:
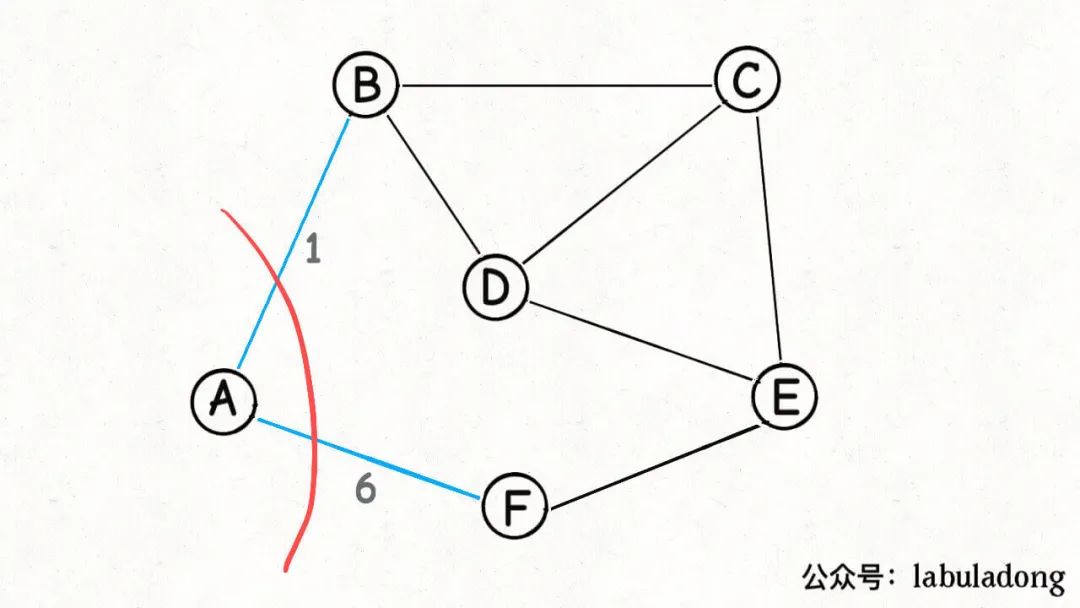
既然這是一個(gè)合法的「切分」,那么按照切分定理,這些「橫切邊」AB, AF中權(quán)重最小的邊一定是最小生成樹(shù)中的一條邊:
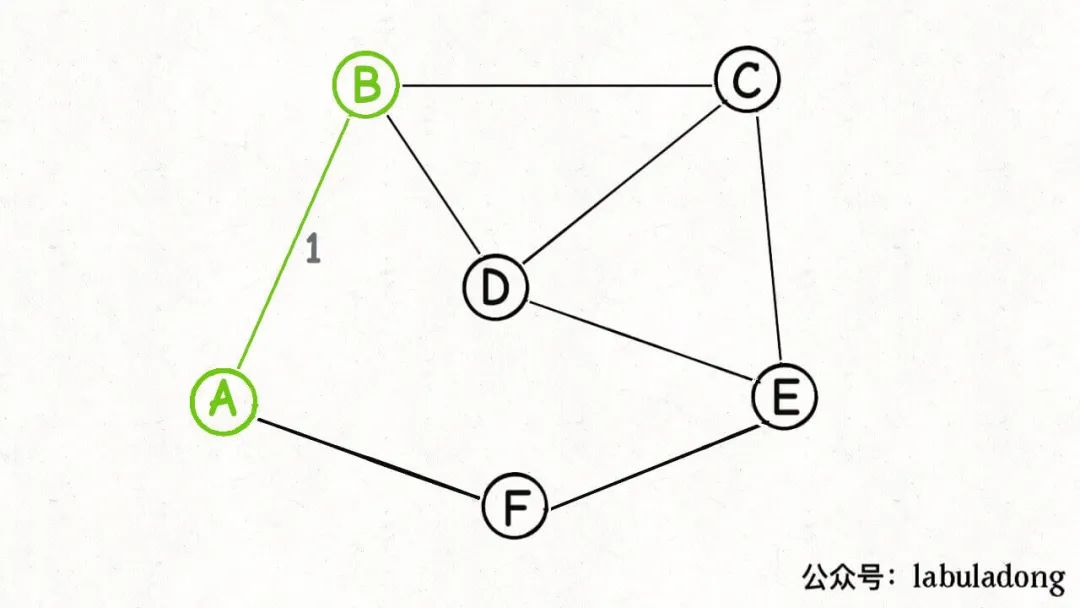
好,現(xiàn)在已經(jīng)找到最小生成樹(shù)的第一條邊(邊AB),然后呢,如何安排下一次「切分」?
按照 Prim 算法的邏輯,我們接下來(lái)可以圍繞A和B這兩個(gè)節(jié)點(diǎn)做切分:
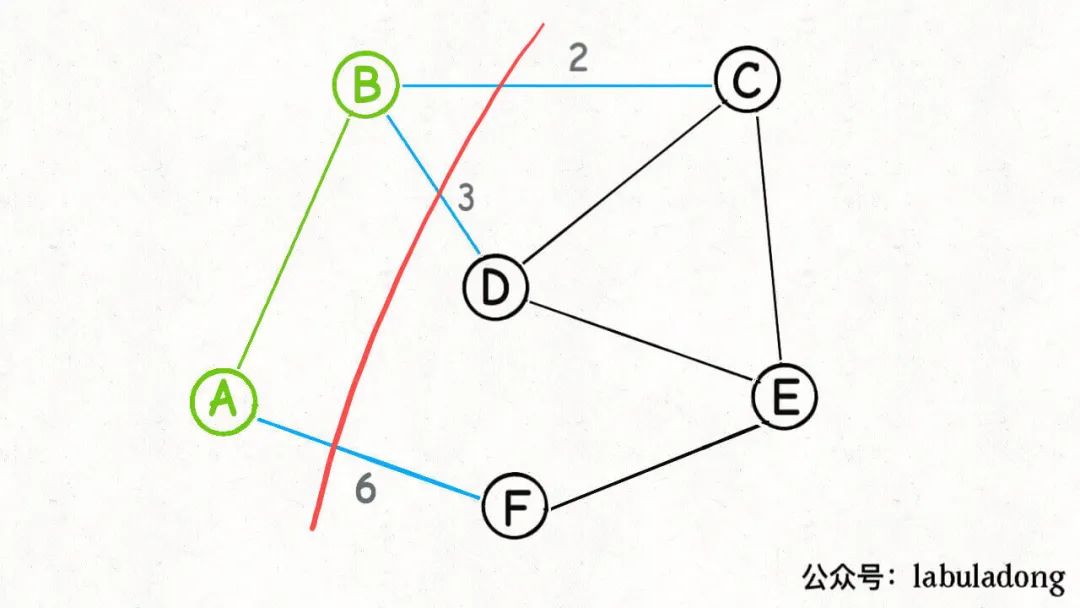
然后又可以從這個(gè)切分產(chǎn)生的橫切邊(圖中藍(lán)色的邊)中找出權(quán)重最小的一條邊,也就又找到了最小生成樹(shù)中的第二條邊BC:
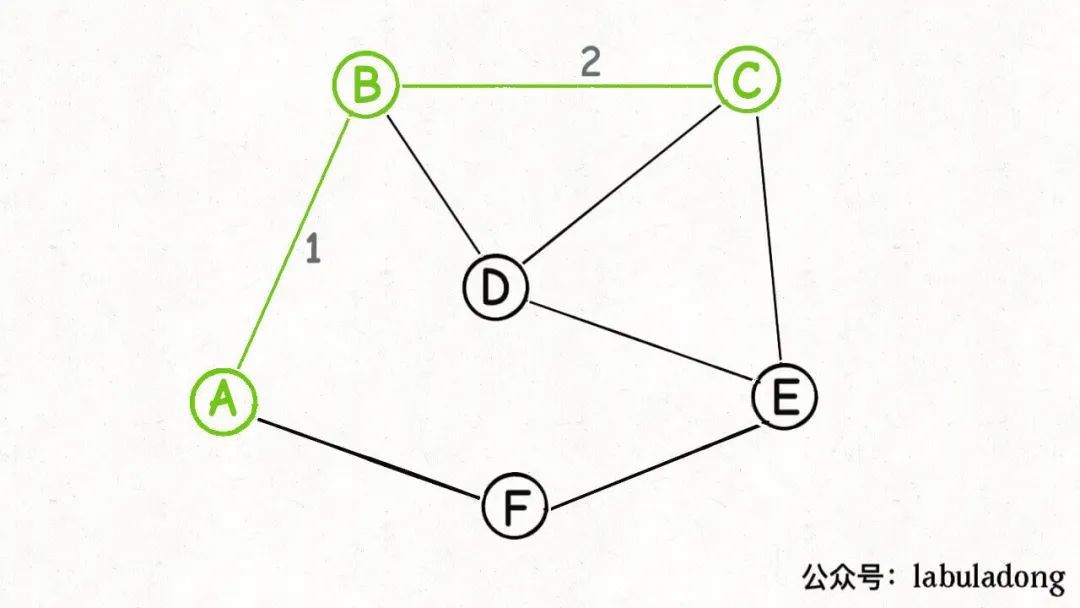
接下來(lái)呢?也是類(lèi)似的,再圍繞著A, B, C這三個(gè)點(diǎn)做切分,產(chǎn)生的橫切邊中權(quán)重最小的邊是BD,那么BD就是最小生成樹(shù)的第三條邊:
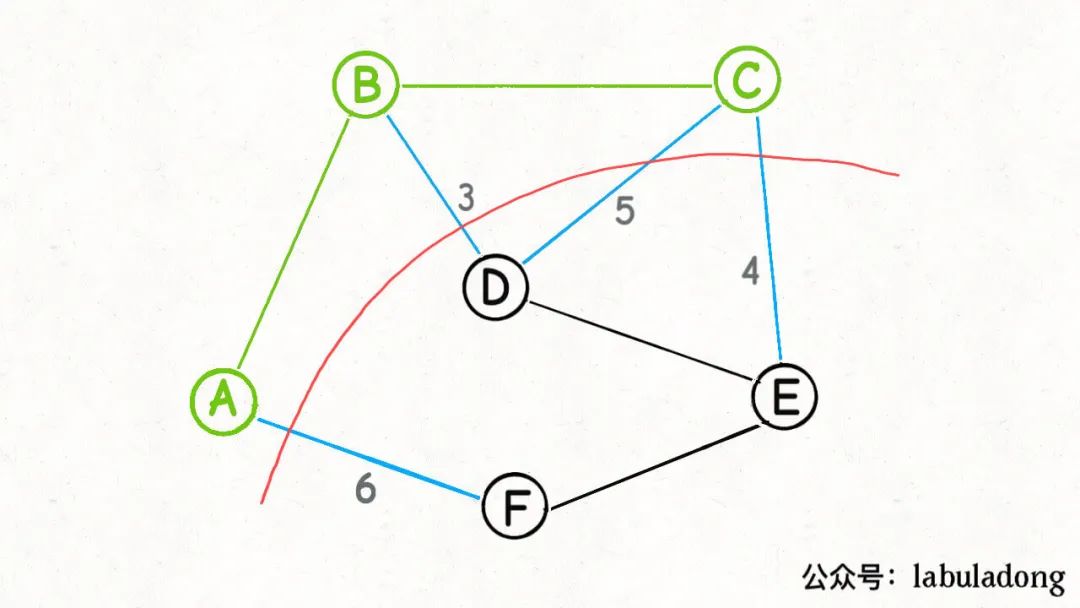
接下來(lái)再圍繞A, B, C, D這四個(gè)點(diǎn)做切分……
Prim 算法的邏輯就是這樣,每次切分都能找到最小生成樹(shù)的一條邊,然后又可以進(jìn)行新一輪切分,直到找到最小生成樹(shù)的所有邊為止。
這樣設(shè)計(jì)算法有一個(gè)好處,就是比較容易確定每次新的「切分」所產(chǎn)生的「橫切邊」。
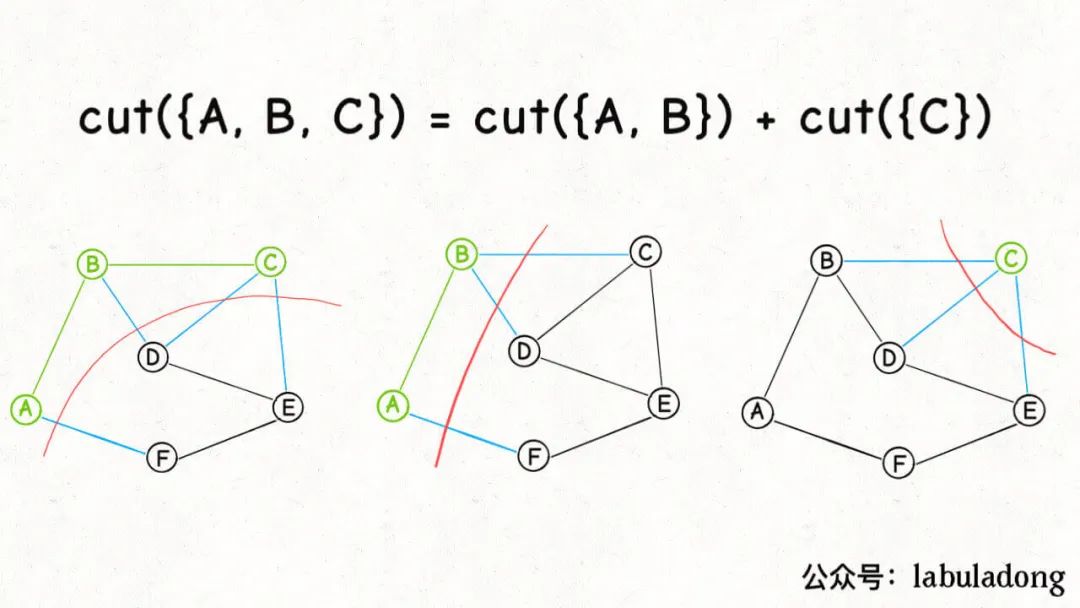
比如回顧剛才的圖,當(dāng)我知道了節(jié)點(diǎn)A, B的所有「橫切邊」(不妨表示為cut({A, B})),也就是圖中藍(lán)色的邊:

是否可以快速算出cut({A, B, C}),也就是節(jié)點(diǎn)A, B, C的所有「橫切邊」有哪些?

是可以的,因?yàn)槲覀儼l(fā)現(xiàn):
cut({A,B,C})=cut({A,B})+cut({C})
而cut({C})就是節(jié)點(diǎn)C的所有鄰邊:
這個(gè)特點(diǎn)使我們用我們寫(xiě)代碼實(shí)現(xiàn)「切分」和處理「橫切邊」成為可能:
在進(jìn)行切分的過(guò)程中,我們只要不斷把新節(jié)點(diǎn)的鄰邊加入橫切邊集合,就可以得到新的切分的所有橫切邊。
當(dāng)然,細(xì)心的讀者肯定發(fā)現(xiàn)了,cut({A, B})的橫切邊和cut({C})的橫切邊中BC邊重復(fù)了。
不過(guò)這很好處理,用一個(gè)布爾數(shù)組inMST輔助,防止重復(fù)計(jì)算橫切邊就行了。
最后一個(gè)問(wèn)題,我們求橫切邊的目的是找權(quán)重最小的橫切邊,怎么做到呢?
很簡(jiǎn)單,用一個(gè)優(yōu)先級(jí)隊(duì)列存儲(chǔ)這些橫切邊,就可以動(dòng)態(tài)計(jì)算權(quán)重最小的橫切邊了。
明白了上述算法原理,下面來(lái)看一下 Prim 算法的代碼實(shí)現(xiàn):
classPrim{
//核心數(shù)據(jù)結(jié)構(gòu),存儲(chǔ)「橫切邊」的優(yōu)先級(jí)隊(duì)列
privatePriorityQueue<int[]>pq;
//類(lèi)似visited數(shù)組的作用,記錄哪些節(jié)點(diǎn)已經(jīng)成為最小生成樹(shù)的一部分
privateboolean[]inMST;
//記錄最小生成樹(shù)的權(quán)重和
privateintweightSum=0;
//graph是用鄰接表表示的一幅圖,
//graph[s]記錄節(jié)點(diǎn)s所有相鄰的邊,
//三元組int[]{from,to,weight}表示一條邊
privateList<int[]>[]graph;
publicPrim(List<int[]>[]graph){
this.graph=graph;
this.pq=newPriorityQueue<>((a,b)->{
//按照邊的權(quán)重從小到大排序
returna[2]-b[2];
});
//圖中有n個(gè)節(jié)點(diǎn)
intn=graph.length;
this.inMST=newboolean[n];
//隨便從一個(gè)點(diǎn)開(kāi)始切分都可以,我們不妨從節(jié)點(diǎn)0開(kāi)始
inMST[0]=true;
cut(0);
//不斷進(jìn)行切分,向最小生成樹(shù)中添加邊
while(!pq.isEmpty()){
int[]edge=pq.poll();
intto=edge[1];
intweight=edge[2];
if(inMST[to]){
//節(jié)點(diǎn)to已經(jīng)在最小生成樹(shù)中,跳過(guò)
//否則這條邊會(huì)產(chǎn)生環(huán)
continue;
}
//將邊edge加入最小生成樹(shù)
weightSum+=weight;
inMST[to]=true;
//節(jié)點(diǎn)to加入后,進(jìn)行新一輪切分,會(huì)產(chǎn)生更多橫切邊
cut(to);
}
}
//將s的橫切邊加入優(yōu)先隊(duì)列
privatevoidcut(ints){
//遍歷s的鄰邊
for(int[]edge:graph[s]){
intto=edge[1];
if(inMST[to]){
//相鄰接點(diǎn)to已經(jīng)在最小生成樹(shù)中,跳過(guò)
//否則這條邊會(huì)產(chǎn)生環(huán)
continue;
}
//加入橫切邊隊(duì)列
pq.offer(edge);
}
}
//最小生成樹(shù)的權(quán)重和
publicintweightSum(){
returnweightSum;
}
//判斷最小生成樹(shù)是否包含圖中的所有節(jié)點(diǎn)
publicbooleanallConnected(){
for(inti=0;iif(!inMST[i]){
returnfalse;
}
}
returntrue;
}
}
明白了切分定理,加上詳細(xì)的代碼注釋,你應(yīng)該能夠看懂 Prim 算法的代碼了。
這里我們可以再回顧一下本文開(kāi)頭說(shuō)的 Prim 算法和Kruskal 算法的聯(lián)系:
Kruskal 算法是在一開(kāi)始的時(shí)候就把所有的邊排序,然后從權(quán)重最小的邊開(kāi)始挑選屬于最小生成樹(shù)的邊,組建最小生成樹(shù)。
Prim 算法是從一個(gè)起點(diǎn)的切分(一組橫切邊)開(kāi)始執(zhí)行類(lèi)似 BFS 算法的邏輯,借助切分定理和優(yōu)先級(jí)隊(duì)列動(dòng)態(tài)排序的特性,從這個(gè)起點(diǎn)「生長(zhǎng)」出一棵最小生成樹(shù)。
說(shuō)到這里,Prim 算法的時(shí)間復(fù)雜度是多少呢?
這個(gè)不難分析,復(fù)雜度主要在優(yōu)先級(jí)隊(duì)列pq的操作上,由于pq里面裝的是圖中的「邊」,假設(shè)一幅圖邊的條數(shù)為E,那么最多操作O(E)次pq。每次操作優(yōu)先級(jí)隊(duì)列的時(shí)間復(fù)雜度取決于隊(duì)列中的元素個(gè)數(shù),取最壞情況就是O(logE)。
所以這種 Prim 算法實(shí)現(xiàn)的總時(shí)間復(fù)雜度是O(ElogE)。回想一下Kruskal 算法,它的時(shí)間復(fù)雜度主要是給所有邊按照權(quán)重排序,也是O(ElogE)。
不過(guò)話說(shuō)回來(lái),和前文Dijkstra 算法類(lèi)似,Prim 算法的時(shí)間復(fù)雜度也是可以優(yōu)化的,但優(yōu)化點(diǎn)在于優(yōu)先級(jí)隊(duì)列的實(shí)現(xiàn)上,和 Prim 算法本身的算法思想關(guān)系不大,所以我們這里就不做討論了,有興趣的讀者可以自行搜索。
接下來(lái),我們實(shí)操一波,把之前用 Kruskal 算法解決的力扣題目運(yùn)用 Prim 算法再解決一遍。
題目實(shí)踐
第一題是力扣第 1135 題「最低成本聯(lián)通所有城市」,這是一道標(biāo)準(zhǔn)的最小生成樹(shù)問(wèn)題:
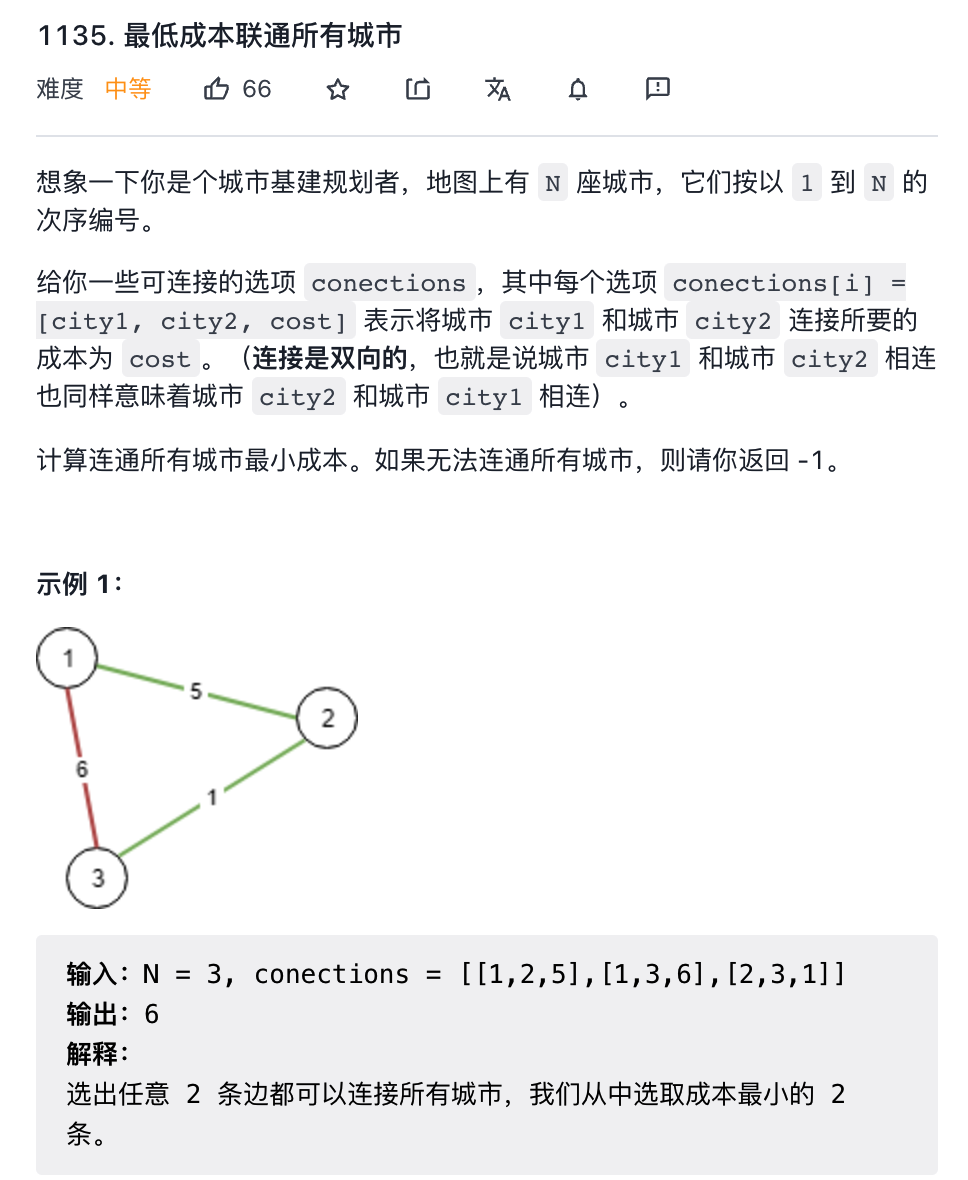
函數(shù)簽名如下:
intminimumCost(intn,int[][]connections);
每座城市相當(dāng)于圖中的節(jié)點(diǎn),連通城市的成本相當(dāng)于邊的權(quán)重,連通所有城市的最小成本即是最小生成樹(shù)的權(quán)重之和。
那么解法就很明顯了,我們先把題目輸入的connections轉(zhuǎn)化成鄰接表形式,然后輸入給之前實(shí)現(xiàn)的Prim算法類(lèi)即可:
publicintminimumCost(intn,int[][]connections){
//轉(zhuǎn)化成無(wú)向圖鄰接表的形式
List<int[]>[]graph=buildGraph(n,connections);
//執(zhí)行Prim算法
Primprim=newPrim(graph);
if(!prim.allConnected()){
//最小生成樹(shù)無(wú)法覆蓋所有節(jié)點(diǎn)
return-1;
}
returnprim.weightSum();
}
List<int[]>[]buildGraph(intn,int[][]connections){
//圖中共有n個(gè)節(jié)點(diǎn)
List<int[]>[]graph=newLinkedList[n];
for(inti=0;inewLinkedList<>();
}
for(int[]conn:connections){
//題目給的節(jié)點(diǎn)編號(hào)是從1開(kāi)始的,
//但我們實(shí)現(xiàn)的Prim算法需要從0開(kāi)始編號(hào)
intu=conn[0]-1;
intv=conn[1]-1;
intweight=conn[2];
//「無(wú)向圖」其實(shí)就是「雙向圖」
//一條邊表示為int[]{from,to,weight}
graph[u].add(newint[]{u,v,weight});
graph[v].add(newint[]{v,u,weight});
}
returngraph;
}
classPrim{/*見(jiàn)上文*/}
關(guān)于buildGraph函數(shù)需要注意兩點(diǎn):
一是題目給的節(jié)點(diǎn)編號(hào)是從 1 開(kāi)始的,所以我們做一下索引偏移,轉(zhuǎn)化成從 0 開(kāi)始以便Prim類(lèi)使用;
二是如何用鄰接表表示無(wú)向加權(quán)圖,前文圖論算法基礎(chǔ)說(shuō)過(guò)「無(wú)向圖」其實(shí)就可以理解為「雙向圖」。
這樣,我們轉(zhuǎn)化出來(lái)的graph形式就和之前的Prim算法類(lèi)對(duì)應(yīng)了,可以直接施展 Prim 算法計(jì)算最小生成樹(shù)。
再來(lái)看看力扣第 1584 題「連接所有點(diǎn)的最小費(fèi)用」:
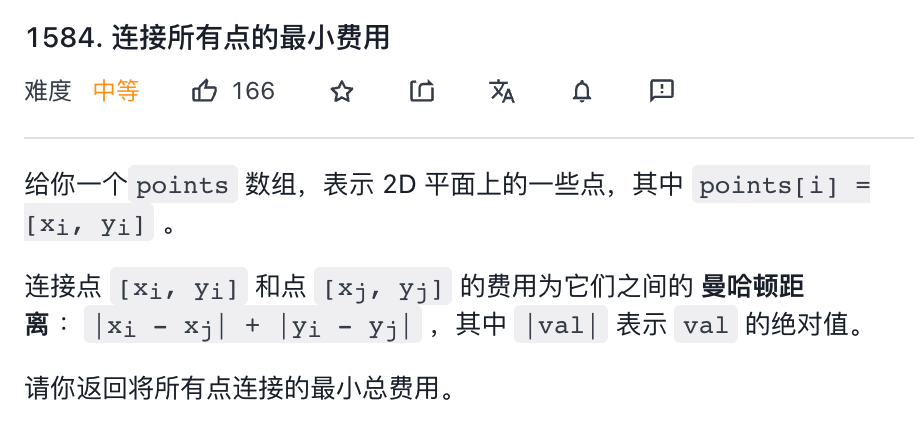
比如題目給的例子:
points=[[0,0],[2,2],[3,10],[5,2],[7,0]]
算法應(yīng)該返回 20,按如下方式連通各點(diǎn):
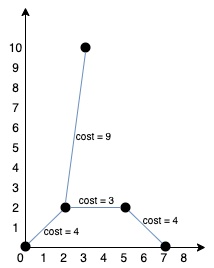
函數(shù)簽名如下:
intminCostConnectPoints(int[][]points);
很顯然這也是一個(gè)標(biāo)準(zhǔn)的最小生成樹(shù)問(wèn)題:每個(gè)點(diǎn)就是無(wú)向加權(quán)圖中的節(jié)點(diǎn),邊的權(quán)重就是曼哈頓距離,連接所有點(diǎn)的最小費(fèi)用就是最小生成樹(shù)的權(quán)重和。
所以我們只要把points數(shù)組轉(zhuǎn)化成鄰接表的形式,即可復(fù)用之前實(shí)現(xiàn)的Prim算法類(lèi):
publicintminCostConnectPoints(int[][]points){
intn=points.length;
List<int[]>[]graph=buildGraph(n,points);
returnnewPrim(graph).weightSum();
}
//構(gòu)造無(wú)向圖
List<int[]>[]buildGraph(intn,int[][]points){
List<int[]>[]graph=newLinkedList[n];
for(inti=0;inewLinkedList<>();
}
//生成所有邊及權(quán)重
for(inti=0;ifor(intj=i+1;jintxi=points[i][0],yi=points[i][1];
intxj=points[j][0],yj=points[j][1];
intweight=Math.abs(xi-xj)+Math.abs(yi-yj);
//用points中的索引表示坐標(biāo)點(diǎn)
graph[i].add(newint[]{i,j,weight});
graph[j].add(newint[]{j,i,weight});
}
}
returngraph;
}
classPrim{/*見(jiàn)上文*/}
這道題做了一個(gè)小的變通:每個(gè)坐標(biāo)點(diǎn)是一個(gè)二元組,那么按理說(shuō)應(yīng)該用五元組表示一條帶權(quán)重的邊,但這樣的話不便執(zhí)行 Prim 算法;所以我們用points數(shù)組中的索引代表每個(gè)坐標(biāo)點(diǎn),這樣就可以直接復(fù)用之前的 Prim 算法邏輯了。
到這里,Prim 算法就講完了,整個(gè)圖論算法也整的差不多了,更多精彩文章,敬請(qǐng)期待。
原文標(biāo)題:Prim 算法,YYDS
文章出處:【微信公眾號(hào):算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
審核編輯:湯梓紅
-
算法
+關(guān)注
關(guān)注
23文章
4613瀏覽量
92945 -
計(jì)算
+關(guān)注
關(guān)注
2文章
450瀏覽量
38816 -
檢測(cè)
+關(guān)注
關(guān)注
5文章
4490瀏覽量
91489
原文標(biāo)題:Prim 算法,YYDS
文章出處:【微信號(hào):TheAlgorithm,微信公眾號(hào):算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
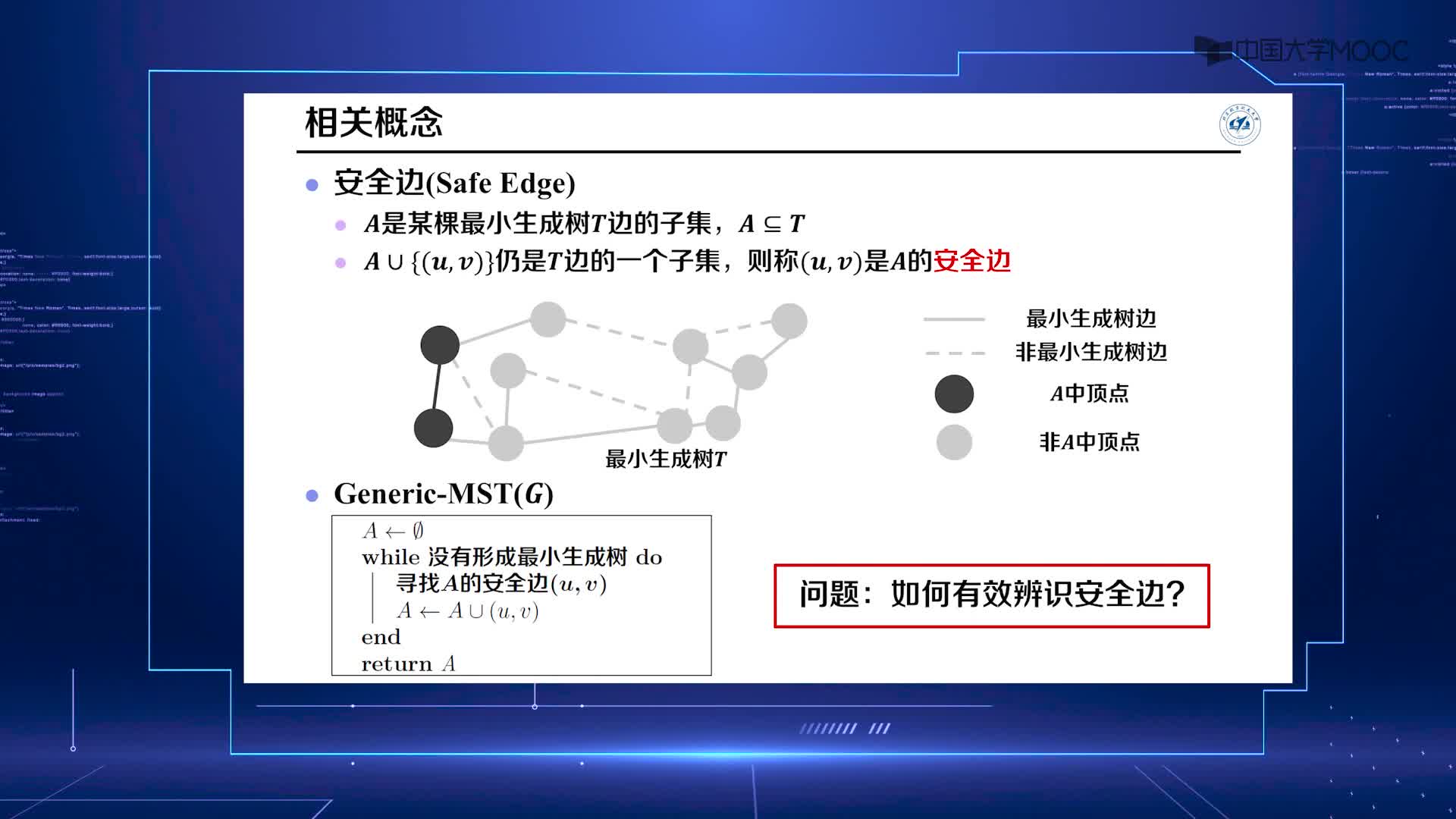
算法設(shè)計(jì)與分析:10.1 最小生成樹(shù):Prim算法(2)(2)#硬聲創(chuàng)作季
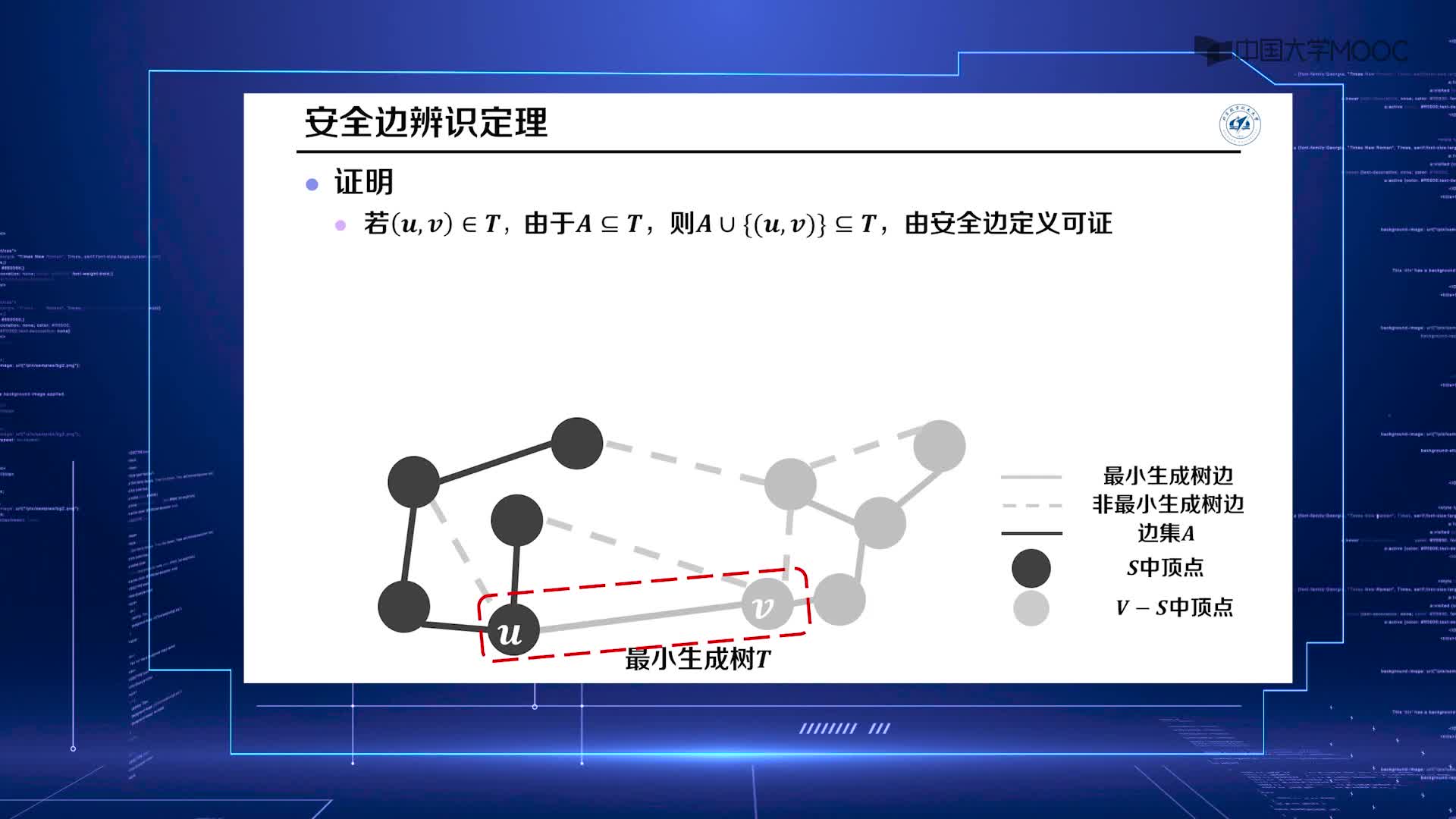
算法設(shè)計(jì)與分析:10.1 最小生成樹(shù):Prim算法(2)(3)#硬聲創(chuàng)作季

算法設(shè)計(jì)與分析:10.1 最小生成樹(shù):Prim算法(3)(1)#硬聲創(chuàng)作季

算法設(shè)計(jì)與分析:10.1 最小生成樹(shù):Prim算法(4)(1)#硬聲創(chuàng)作季
matlab經(jīng)典算法的程序集合
了解一下STM32的時(shí)鐘樹(shù)
基于故障樹(shù)最小割集求解算法
基于Prim初始種群選取優(yōu)化遺傳算法的三維片上網(wǎng)絡(luò)低功耗映射
Prim算法以及優(yōu)化實(shí)現(xiàn)
如何使用最優(yōu)最小生成樹(shù)進(jìn)行三維模型形狀優(yōu)化方法的詳細(xì)資料說(shuō)明
MATLAB建模算法和程序資料合集免費(fèi)下載





 一文詳細(xì)了解Prim最小生成樹(shù)算法
一文詳細(xì)了解Prim最小生成樹(shù)算法










評(píng)論