1.高斯濾波算法的實現
前面講的均值/中值濾波,對于濾波窗口內每個像素的權重都是一樣的。但是噪聲在圖像當中常表現為異常視覺效果的孤立像素點或像素塊,那么他必然不是平均分布。
這里先引入一個概念:正態分布:
正態分布是最重要的一種概率分布,相關概念是由德國的數學家和天文學家Moivre在1733年提出的,但由于德國數學家Gauss率先將其用于天文學研究,因此也叫做高斯分布。在正態分布里,認為中間狀態是常態,過高和過低都屬于少數,因此正態分布具有相當的普遍性,典型的比如我們的身高、壽命、血壓、成績、測量誤差等都遵從正太分布。
以中國家庭動態跟蹤,抽樣掉找自報的身高數據為例,如下是2010年男/女身高分布直方圖,近似呈現正態分布。
扯遠了,回歸正題,我們這里主題就是要處理高斯分布的噪聲,與椒鹽噪聲不同,高斯噪聲則是畫面上每個點都存在著不同程度的,與當前像素距離成高斯分布的噪聲。這里我們繼續在前文已經成熟的3*3滑窗方案上,進行高斯算法的講解,及Matlab&FPGA的實現。
2.高斯濾波算法理論
根據概率論及中心極限定理(MBA智庫百科,全球專業中文經管百科)猜想,大部分噪聲應該也符合正態分布/高斯分布(高斯白噪聲),所以也就有了高斯濾波,及根據正態分布進行權重計算的濾波方法。
我們已經介紹了高斯分布(正態分布),此處我們直接引入高斯分布函數,為一維與二維高斯分布函數,其中σ為高斯分布的強度,σ越大則數據更越分散,反之則越向中心集中分布:
我們首先采用Matlab自帶的高斯函數來驗證一下結果,σ=1的高斯濾波,可見有一定的模糊效果。圖3為5*5的窗口,σ=3的高斯濾波,模糊的強度稍微更大了一點。圖4為11*11的窗口,σ=3的高斯濾波,相對5*5窗口,σ=3的濾波,可見擴大擴大窗口后,濾波后模糊程度非常大,可見濾波窗口對濾波的強度影響更大,其次才是σ的大小。
左側為生成5*5模板的Matlab代碼,我們先根據高斯分布的公式生成5*5 的模板。其中11行為原始二維高斯分布的函數,而12行中我已經將常熟去掉,畢竟后續需要歸一化,就可以簡化公式,得到的高斯權重分布如有圖G1所示,為一堆浮點數據。
但是,二維高斯分布并不僅僅在5*5的區間內,權重在5*5之外仍然有分布,只不過我們當前采用5*5的高斯分布,權且認為數據主要分布在5*5之內,因此還需要進一步的歸一化,來使得所有權中之和=1,如17-18行所示,得到右邊第二個表格數據的模板。
如果在Matlab中實現,此時得到的模板已經可以用于高斯濾波卷積計算。但我們的目標是FPGA實現,因此還需要進一步定點化,這里采用*1024為例,生成最終的5*5的模板如上第三個表格所示。當然最后需要/1024縮放回去,使得結果最終還原到0-255。
為Matlab進行5*5高斯模板卷積的源代碼,其中IMG1為原圖,IMG2為采用Matlab自帶高斯濾波函數在σ=3,5*5窗口下的濾波結果,IMG3為我們手動編寫的,根據生成的定點化模板卷積后的結果。
其中在處理5*5卷積時,為了設計的簡便,邊緣像素采用了復制原值的操作。另外,由于Matlab是浮點運算,在卷積后將數據類型再次轉成uint8定點。最后執行生成的結果如下圖所示,其中圖2為與圖3,處理結果幾乎一樣,我們定點化5*5高斯模板算法成功。
責任編輯:haq
-
FPGA
+關注
關注
1630文章
21759瀏覽量
604326 -
matlab
+關注
關注
185文章
2979瀏覽量
230651
原文標題:高斯濾波算法之Matlab&FPGA實現
文章出處:【微信號:FPGA_Study,微信公眾號:FPGA自習室】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
【「從算法到電路—數字芯片算法的電路實現」閱讀體驗】+內容簡介
基于FPGA實現FIR數字濾波器
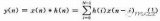
STM32的ADC采樣及各式濾波算法實現




 FPGA中高斯濾波算法的實現
FPGA中高斯濾波算法的實現











評論