“定位”這個概念想必大家并不陌生,可以說定位技術的迅猛發展,給我們的日常生活帶來了極大的便利。
比如,手機的定位導航系統讓“路癡”再也不怕出遠門了;航天飛行器可以自由地穿梭于浩瀚的宇宙卻逃不出人類的掌控;無人駕駛技術更是離不開定位系統的支撐……
接下來,將向大家介紹一種簡單的定位算法:三邊測距定位算法。
【簡介】
簡單地說,實現定位你只需要做好以下兩點:
測量值 從某種意義上說,幾乎所有你能測量的數據都取決于“位置”,并且可以利用測得的數據進行定位。最理想的情況是測量那些對“位置”非常敏感的數據。例如,測量溫度可能會知道你身在哪個大陸,當然這樣的結果并不準確,但是如果測量的是你相對于某些點的距離或者角度,那么對你的位置的定位可能會更精確一些。
參考點 描述一個確定的位置,正確的方法就是描述它相對于某些參考點的位置。參考點可以是“你的家”、“北極星”或“天空中的一些衛星”。對我們來說,我們將使用錨。利用3個錨點就可以描述一個二維的坐標系統,在這個系統中我們可以找到我們的位置。對于三維定位系統,我們則需要4個錨點。
下面是一些例子:
定位系統測量值參考點
GPS距離*衛星
Pozyx距離錨
攝像機視頻圖像相機指定方向
WiFi、指紋識別接收信號強度數據庫中的指紋
數字羅盤磁場矢量磁場北極
航位推算加速度和角速度(來自陀螺儀)最初的位置和方向
注意:一些GPS接收器也使用多普勒頻移定位
【三邊測距法】
最常用的定位方法是使用基本的幾何圖形來估計位置。通過測量與錨點的距離,就可以確定你的位置。如果我們只知道自己與錨點的距離,那么我們的位置肯定會在以錨點P為圓心以測得距離d為半徑的圓上。如果我們用3個錨進行距離測量,我們會發現我們的位置在三個圓的交點上,如圖1所示。這種方法被稱為三邊測距法(如果使用的錨點數量超過3個,則稱為多邊測距法)。
這種方法的困難在于測量中總會有一些噪音,測量并不完美。因此,圓不會在一個點相交。為了解決這個問題,我們試著找出最接近所有圓的點。
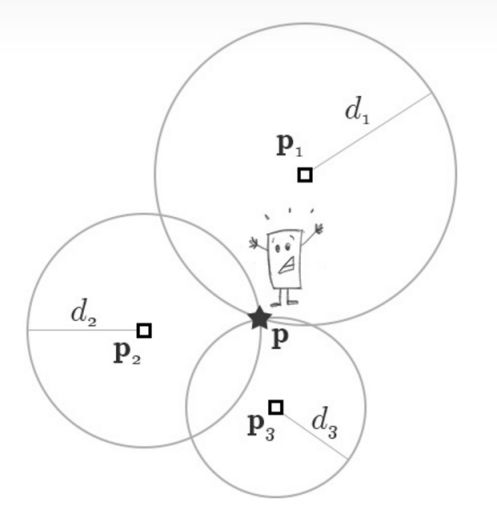
圖1:三邊測量
注:你可以選擇跳過該算法的描述,直接參閱下一篇文章:超寬帶是如何工作的。
【一個基本的算法】
在本節中,我們將介紹一種簡單的算法,它可以從一系列的范圍測量中計算出位置。這個基本算法不是最優的,但是當范圍測量足夠精確時,它就會很好地工作。
我們將解釋2D定位的算法。位置P由坐標x和y給出。第i個錨點pi的位置坐標為(xi,yi),如果我們有N個錨,那么i的取值為從1到N,這些錨點的坐標是已知的。
現在,位置P與第i個錨點之間的距離由di表示,di由下面的公式給出:
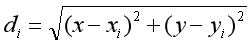
對等式兩邊取平方:
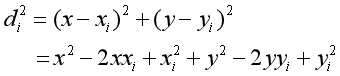
上面方程的問題在于含有非線性項x^2和y^2。我們可以通過從di^2中減去dN^2來消除這些非線性項,得到N-1個方程,其中第i個方程式為:
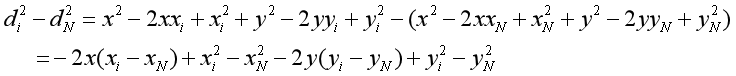
現在我們有了一些關于坐標x和y的線性方程,這很好,因為線性方程很容易求解。我們把它寫成矩陣的形式:
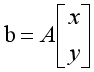
其中:
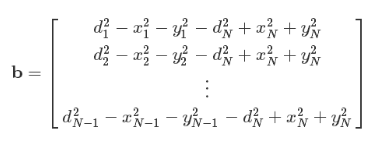
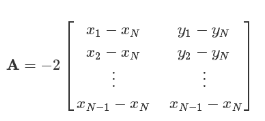
我們現在可以解這個方程組了。
如果我們恰好有3個錨點:N=3,我們就會得到兩個方程來求解兩個未知數,通過求解下面的方程,我們可以找到P的位置:
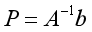
如果我們有超過3個錨點:N》3,我們得到的方程的數量要多于未知數的數量,此時A的逆矩陣是不存在的。為了解決這個問題,我們可以利用偽逆算子來計算這個位置。這就產生了下面的方程式:
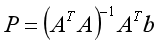
請注意,上面的公式將盡可能地將坐標x和y與所有不同的方程相匹配。因此,當使用更多的錨時,定位的準確性也會隨之提高。
上面描述的算法被稱為線性最小二乘算法。“線性”是因為我們把方程進行了線性化(通過平方)和“最小二乘”是因為矩陣的(偽)逆矩陣會使所有方程的平方誤差最小化。
【拓展】
上面描述的算法是一種非常簡單和低復雜度的算法。如果你想了解更多關于先進定位技術的知識,建議你尋找以下主題:非線性最小二乘、卡爾曼濾波、粒子濾波、置信傳播……
本文來源:平行機器人
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有,如涉及侵權,請后臺聯系小編進行處理。
編輯:jq
-
數據
+關注
關注
8文章
7134瀏覽量
89393 -
指紋識別
+關注
關注
43文章
1743瀏覽量
102316 -
WIFI
+關注
關注
81文章
5308瀏覽量
204447 -
GPS接收器
+關注
關注
0文章
12瀏覽量
8828
原文標題:詳解:三邊測距定位算法
文章出處:【微信號:HXSLH1010101010,微信公眾號:FPGA技術江湖】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
煤礦人員定位技術與功能的全方位分析
如何借助北斗衛星定位終端實現邊坡智能監測預警

毫米波雷達如何提高測距精度
工業環境中的測距與定位應用解決方案
全方位解剖MOS管

主動式藍牙RSSI定位系統和被動式藍牙RSSI定位系統的原理




 全方位剖析三邊測距定位算法
全方位剖析三邊測距定位算法












評論