上一篇所介紹的卡拉比—丘流形（Calabi-Yau manifold），因擁有特殊的拓撲性質，成為解釋弦論中額外6維緊致空間的核心。然而，6維卡拉比—丘流形的拓撲形態眾多，幾何結構非常復雜，難以直觀想象。 因此，一般而言，在以解釋物理圖像為重點，無需細究“額外6維空間”的數學性質時，我們使用緊致化中最簡單的6維環面，來代替復雜的卡拉比—丘流形。通俗地講，我們用比較簡單的環面來代替難以想象的復雜流形。 本篇文章，我們從經典點粒子的運動規律出發，來看看弦理論中“弦”的游戲規則。

1 平坦環面

說到環面，我們經常想到的是甜甜圈形狀，但是拓撲學家們偏向于一種以更抽象的方式來描繪的環面。在圖1a中，我們將二維環面畫成一個長方形。

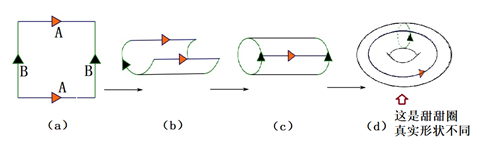
圖1：平坦（2維）環面形成過程，可以想象成將一個桶狀環面之首尾粘合起來，成“甜甜圈”，但有實質性的不同。

圖a的方形中，“A”箭頭所對應的兩條邊將會被粘合在一起，“B”箭頭所對應的兩條邊也將會被粘合在一起。也就是說，如同科幻片中見到的那樣：當你從長方形上方的A邊走出長方形時，你會在下方的A邊上出現；當你穿過長方形右邊的B時，你會在左方的B邊現身。

如此而形成的二維環面，被稱為抽象環面，或平坦環面（Flat Torus）［1］，它的形狀不同于甜甜圈。事實上，如圖1所示：兩條A邊粘合后形成柱面，這第一步沒有任何問題。然而，第二步，當我們將圖c柱面的兩端B 粘合起來后，我們不可能得到真正甜甜圈的形狀，即圖1d所示的那種平滑無皺褶的曲面。這里有一個深層的原因：抽象環面來自于一個平坦的長方形，本質上是平坦的，（內蘊）曲率為零，而通常所見的甜甜圈的內蘊曲率不為零。抽象環面與甜甜圈的內蘊性質不一樣。

盡管抽象環面不能被平滑地嵌入三維空間中，卻很容易依靠想象來理解它的拓撲性質。

最簡單的環面是1維的圓圈，圖1構建的是二維環面，其方法可以推廣到更高的維度。例如，設想一個長方體，它有六個面：（A，A’）、（B，B’）、（C，C’），兩兩互相平行。想象將A和A’粘合在一起，B和B’、C和C’也粘合在一起，便構成了一個3維的抽象環面。同樣的方法可以構建任意n維的抽象環面。

2 弦在時空中的（經典）運動

卡拉比—丘流形或者抽象環面，作為6維緊致空間，加上我們熟悉的、大范圍尺度上展開了的4維時空，構成弦論的10維時空，是“弦”活躍的舞臺。也就是說，弦論中有兩種舞臺：4維時空大舞臺（即我們身處的現實世界）和6維的小舞臺。從數學的角度說，弦論中的空間是4維時空與6維緊致空間的笛卡爾積。

除了舞臺和演員之外，還得有劇本，即游戲規則。對物理學而言，游戲規則又有量子及非量子（經典）之分。

弦在空間的運動規律可以從點粒子的運動規律推廣而來。首先我們看看如何將經典點粒子規則推廣到經典弦。

牛頓力學中，點粒子的軌跡是3維空間中隨時間變化的一條線。相對論中，將粒子在4維時空中運動的軌跡稱為“世界線”，見圖2a。弦論中，0維的點粒子被（更小的）1維的弦運動代替了。弦在時空中運動的軌跡則用軌跡面代替，稱之為“世界面”，如2b所示。更進一步，如果運動的實體是二維的（膜），時空中的運動軌跡便叫做“世界體”，如圖2c所示。

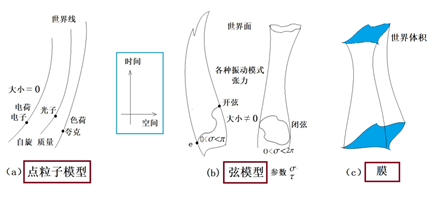
圖2：粒子vs弦（或膜）

相對于無大小的點粒子數學模型而言，弦模型有許多優越性，其中一點便是避開了點粒子的無窮大問題。

在經典電子學中就存在無窮大的困難。經典物理中，可以將電子當作一個半徑r的小球，電子的質量公式為m = e2/rc2。當r趨近于0時，質量成為無窮大。最后，經典電子論通過引進電子的有限半徑（非點粒子）免除了這一發散。在量子場論中，則需要使用重整化的方法消除無窮大，但引力場不能重整化，從而使它不能被包括到標準模型中。

然而，對弦論而言，重整化變得無關緊要，因為弦不是點，弦有尺寸大小，自然而然地去除了點粒子的發散問題。

3 量子的弦和相互作用

圖2中點粒子和弦運動的類比，很容易推廣到其它情形，包括量子弦及相互作用的情形。也就是說，點粒子時的線，在弦論中則用帶狀曲面（開弦）或管道面（閉弦）來代替（圖2b所示）。

例如，圖2a中的世界線，是經典粒子在4維時空中的軌跡。兩個固定點之間的經典路徑只有一條，但如果考慮量子力學，一個粒子從A到B的路徑有無窮多條，經典路徑（藍色線）只是其中一條（見圖3a）。圖3b顯示的弦論中的情況也類似：除了藍色代表的經典世界面之外，所有可能的世界面都對計算弦A到弦B的量子概率幅有貢獻。

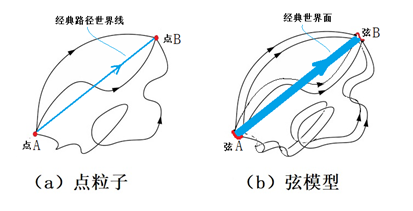
圖3：路徑積分（量子化）

根據量子場論，時空中的粒子，總是在不斷地湮滅，又不斷地產生。產生和湮滅一類的相互作用現象用各級費曼圖來進行描述和計算，弦論也不例外，只是如上所述，相應的線段需要用“面”來替代而已，見圖4。

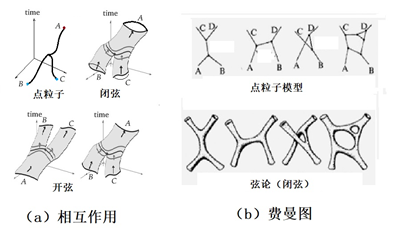
圖4：弦論中弦與弦的相互作用和費曼圖

從場論的角度，比較標準模型來說，弦論的另一個優點是更為簡化。量子場論在數學上可以有無窮多種，因此可對應于無窮多種粒子。比如說，對應于標準模型的61種基本粒子，便有61種不同的量子場論。而在弦論中，只需要一種描述“弦”的量子場論就可以了，由此從概念上得以簡化。

4 膜-弦概念的擴展

在圖2c中，我們已經提及“膜”的概念，它最早來自于與弦論相關的超引力理論（supergravity theory）。如今的弦論中經常談到的膜，有p膜和D膜。

稱為p膜（p-brane）的物理實體，是將點粒子的概念推廣至1維、2維以及更高維度而產生的。舉例來說，點粒子可以被視為0維的膜，而弦則可視為1維的膜，通常意義上的“膜”是2維的。此外，也可能存在更高維的膜。

p膜是動力學物體，在時空中行進時，所根據的是量子力學的規則。它們帶有質量與其他性質，例如電荷。一個p膜在時空中的行進，掃出了（p+1）維度的體積，稱之為世界體積（worldvolume）如圖2c所示。

另一類膜叫做D膜（d-brane），表示符合狄利克雷邊界條件（Dirichlet boundary condition）的膜。D膜是弦論中一類很重要的膜，與開弦在時空中的運動有關。當開弦在時空中行進時，開弦的端點必須在D膜上。對D膜的研究導出了與對偶性有關的重要成果，下一篇的文章中會給以簡單介紹。

5 弦在緊致空間中運動的特殊性

本文開始時曾經提到過：弦論的空間分為伸展的大空間和卷曲的小空間。使用前面文章“電纜線上螞蟻”的比喻：我們看見的電纜線是1維大空間，而線上的螞蟻則能看見另一維卷曲的圓圈（小空間）。

弦論中的大時空是4維的，卷曲緊致的小空間是6維的。4維和6維都無法用平面圖像顯示出來，但是，為了方便解釋概念，我們將弦論的10維時空簡化為圖6a的長長圓柱體，看起來像是螞蟻眼中的2維電纜線。用沿著電纜線方向的那一維，代表4維大時空；用電線的截面圓圈，代表6維小空間。使用如此比喻的話，10維時空中的開弦閉弦，就是電纜線上的小螞蟻了。

也就是說，圖6中無限延伸的x方向代表我們熟知的4維時空，y方向卷曲的小圓代表6個額外小維度。這個6維空間可以是卡拉比-丘流形，也可以簡單地理解成本篇所說的6維抽象環面。對6維環面而言，圖中的R就不是1個數值而應該被理解為代表6個數值了。

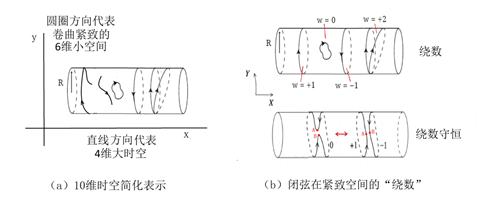
圖6：弦論空間和“繞數”的示意圖

從點粒子到弦論，并非所有物理量都有相應的類比物，弦的特殊性會產生某些點粒子模型中沒有的性質，我們舉閉弦在緊致空間中的“繞數”［2］為例，它就是4維時空的標準模型中沒有的物理量。

如圖6所示，10維時空分成一大一小，其中弦的運動也可以從這兩個方面的運動來討論。也就是說：弦，除了在大的4維時空中運動外，還能繞著緊致空間運動。閉弦的這種運動尤其特殊，因為閉弦可能有一種特別的狀態，就是繞在某一個（或多個）緊致的維度上，可以繞上1圈、2圈或者很多（N）圈，見圖6b。于是，閉弦便多了一種量子態，用一個新的量子數表征這個量子態，叫做“繞數”（winding number）。

開弦沒有繞數的概念，因為開弦在拓撲上等效于一個點，“繞”不起來。

當纏繞在緊致維度上的閉弦發生相互作用時，總繞數是一個守恒量。

圖6b上方的圖，舉出了繞數w=0、+2、+1、-1的例子，下方一圖表示了一個閉弦的變化（等效）過程（從左到右），可用以簡單地說明繞數守恒：開始時，閉弦只是放在圓柱上，沒有繞圈，因此w=0。閉弦上的點A和B接近后相互作用，成為w=1和 w=-1的兩個閉弦，但繞數的總和仍然為0。

怎么樣，你是否理解了點粒子與弦玩法上的不同呢？很好理解是不是？

責任編輯：lq6