提到愛因斯坦,很多人的第一反應就是E=mc2。
沒辦法,質能方程看起來“太簡單”了:左邊的E代表能量,右邊的m代表質量,c是光速,都是中學生就能看懂的物理量。而且,這個方程看起來太神奇了,它告訴我們一般物體都蘊含了巨大的能量,原子彈那毀天滅地的力量就是最好的證明。
又簡單又神奇,不傳播你傳播誰?
但是,很多人容易忘記一件事:質能方程是狹義相對論的結論,需要站在狹義相對論的立場上才能精準地把握它。否則就容易望文生義,再類比、推廣一下,后果就很可怕了。
比如,有人認為質能方程的意思是“質量可以轉化成能量”,或者說“物質可以轉化成能量”。延伸一下,物質代表“有”,能量代表“無”,質能方程暗示著“有無相生”,接下來歡迎進入太極物理頻道……
也有人認為質能方程是在說“質量是能量的一種形式”。延伸一下,我們的物質本質上都是能量,一切都是能量,一切都是虛無,色即是空,接下來歡迎進入相對論佛學頻道……
這種誤解以及可怕的延伸,我還可以列很多。要不是建了那么多社群,見識了各種各樣的人,我真難以想象質能方程會有如此豐富的“內涵和外延”。
不過,想想也不奇怪。畢竟誰都可以談一下質能方程,談的人多了,想法自然就多了。而且,質量虧損這個名字也很容易把大家往歪路上引。
那么,我們就來好好看一看質能方程,看看E=mc2到底是怎么回事,看看它是如何從狹義相對論推導出來的,以及如何正確地對待質能方程。
01從狹義相對論出發
因為質能方程是狹義相對論的產物,所以,想搞清楚質能方程就得先搞清楚狹義相對論。
什么是狹義相對論呢?
《相對論誕生:愛因斯坦是如何創立狹義相對論的?| 主線》里詳細描述了狹義相對論的誕生過程,看完文章的朋友肯定都知道:狹義相對論的核心是洛倫茲協變性。
它跟牛頓力學的核心區別是:狹義相對論的物理定律在洛倫茲變換下保持數學形式不變,而牛頓力學的物理定律在伽利略變換下保持數學形式不變。至于尺縮、鐘慢、雙生子之類的效應,都是狹義相對論的一些簡單結論。
質能方程E=mc2也是這樣。
也就是說,只要我們認為物理定律應該在洛倫茲變換下保持數學形式不變(狹義相對論精神),我們就能推出質能方程E=mc2,而不需要其它的假設和限制。
因此,只要狹義相對論成立,質能方程就成立,它的適用范圍是極廣的。有些朋友認為質能方程只在核反應里才有效,這顯然不對,因為狹義相對論并不是只在核反應里才有效。
那狹義相對論在哪些地方成立呢?是不是像有些人認為的,狹義相對論只在高速(近光速)情況下成立,在低速情況下就必須使用牛頓力學?
不不不,也不是這樣的邏輯。
狹義相對論跟牛頓力學并不是互補的關系。牛頓力學只在低速時適用沒錯,但狹義相對論不僅在高速時適用,在低速時也同樣適用。而且,在低速時它的精度比牛頓力學還要高。
也就是說,狹義相對論不管在低速、高速時都成立,牛頓力學只是狹義相對論在低速情況下一個還算不錯的近似。既然狹義相對論的適用范圍那么廣,質能方程的適用范圍自然也很廣,而不是只局限在核反應里。
但是,愛因斯坦并不需要知道核反應里質量和能量的關系,他直接從狹義相對論的基本原理出發,就無可辯駁地得到了E=mc2。這是最讓人震驚的地方,也是理性的巨大勝利。
接下來,我們就來看一看,看看為什么只要堅持狹義相對論的基本原理,只要堅持物理定律在洛倫茲變換下保持數學形式不變(洛倫茲協變性),我們就能得到質能方程E=mc2。
02動量守恒定律
再來看看E=mc2,公式的左邊出現了能量E,看到能量我們就會想起能量守恒定律。既然是定律,那我們就要問了:你可不可以在洛倫茲變換下保持數學形式不變啊?如果可以,那就歡迎進入狹義相對論的世界;如果不行,那就從哪來回哪去,一邊玩去。
不過,考慮到能量的種類太多太雜,我們先來看看更簡單的動量守恒定律。
在牛頓力學里,動量的定義是mv(質量乘以速度),在不受外力或合外力為0時,兩物體碰撞時動量守恒。
比如,兩個質量都為m的小球以相等的速度v迎面撞上,碰撞后兩個小球黏在了一起。如果以某個小球的運動方向為正(假設為向右),那這個小球的動量就是mv,另一個小球的動量就是-mv,碰撞前動量之和就是mv+(-mv)=0。
根據動量守恒定律,碰撞后小球的總動量也應該為0。而碰撞后它們又黏在了一起,變成了一個質量為2m的大球,所以碰撞后的速度就必然為0(不然總動量就不為0了)。
兩個質量相等、速度相反的小球迎面相撞,碰撞后兩個小球黏在一起并保持靜止。這個事情很容易理解,不管是用牛頓力學的動量守恒定律來計算,還是根據常識來判斷都沒錯。
但是,我們關注的并不是碰撞本身,而是:動量守恒定律是定律么?
這個問題好像很奇怪,動量守恒定律當然是定律了,不然這名字是瞎叫的么?
但是,我希望來到這里的讀者,對定律要有更深層的理解。前面說了,狹義相對論和牛頓力學的核心區別,就是前者的物理定律在洛倫茲變換下保持數學形式不變,后者的物理定律在伽利略變換下保持數學形式不變。
那么,當你把動量定義為mv,當你在說動量守恒定律的時候,這個定律是在洛倫茲變換下保持數學形式不變呢,還是在伽利略變換下保持數學形式不變?如果是前者,那這條動量守恒定律就是狹義相對論下的定律;如果是后者,它就是牛頓力學下的定律。
當然,我們很清楚,把動量定義為mv是牛頓力學里的做法。所以,這樣的動量守恒定律必然是牛頓力學下的定律,它必然能在伽利略變換下保持數學形式不變。
下面我們來簡單地驗證一下。
03伽利略變換
要驗證動量守恒定律是否可以在伽利略變換下保持數學形式不變,我們就要先搞清楚什么是伽利略變換?搞清楚當我們在說一個定律在伽利略變換下保持數學形式不變時,我們到底在說什么?
其實,伽利略變換也好,洛倫茲變換也罷,都是聯系兩個參考系的東西。變換嘛,就是把一個參考系的物理量變到另一個參考系里去。
比如,我在300km/h的高鐵上,覺得前面的椅子速度為0,列車員正以5km/h的速度往車頭走,這是高鐵系的測量結果。
那么,如果我站在地面,地面系測量椅子和列車員的速度又會是多少呢?有同學立馬會說:“我知道,從地面上看,高鐵上椅子的速度是300km/h,列車員的速度是300+5=305km/h。"
如果我問他這樣算的依據是什么,他會覺得這還要什么依據,這不是天經地義的事情么?當然要有依據,物理學是一門非常嚴密的科學,做什么都要有理有據。
我們現在討論的是同一個東西(椅子、列車員)在不同參考系里的速度,這就涉及兩個參考系之間的變換,是一件很嚴肅的事情。如何把這兩個參考系里的物理量聯系起來?答案就是前面說的伽利略變換、洛倫茲變換。
在牛頓力學里,我們用伽利略變換聯系兩個慣性系,那伽利略變換到底長啥樣呢?
假設我們在地面系S建立了一個坐標系(x,y,z,t),現在有一輛火車以速度v沿x軸正方向勻速運動。我們在火車系S’里也建一個坐標系(x’,y’,z’,t’),為了簡化問題,我們讓這兩個坐標系一開始是重合的。
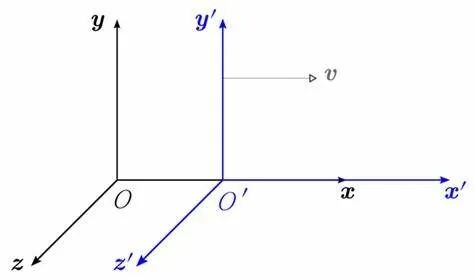
坐標系建好后,空間中發生了任何事件,地面系和火車系都會記錄下這個事件的時空信息(x,y,z記錄空間信息,t記錄時間信息)。我們想知道的就是:地面系和火車系記錄的時空信息之間有什么聯系?
不同的變換會給出不同的答案,伽利略變換的答案是:
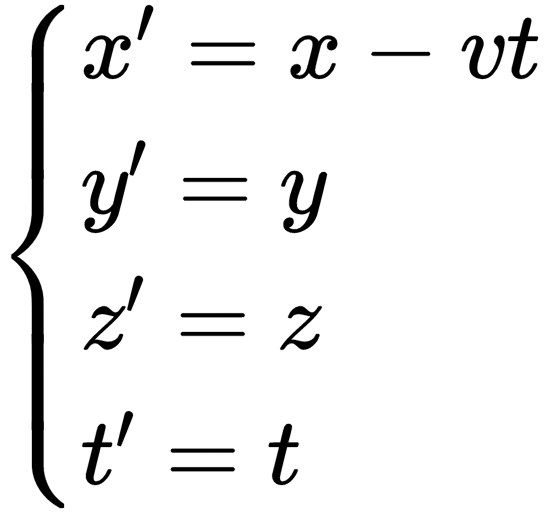
我們知道,牛頓力學里的時間是絕對的,所有參考系的時間都一樣,所以伽利略變換里有t'=t。因為t‘代表火車系的時間,t代表地面系的時間,t'=t不就是說大家的時間都相等,時間是絕對的么?
再看空間,因為火車只沿x軸正方向移動,所以火車系和地面系在y軸和z軸的坐標都一樣,x坐標的關系x'=x-vt也不難理解,琢磨一下就明白了。
有了坐標和時間的關系,我們很容易就能求出火車系的速度u'和地面系的速度u之間的關系:u‘=u-v。這個就不推了,不清楚的可以看看《相對論前夜:牛頓和麥克斯韋的戰爭》,里面有更加詳細的推導。
伽利略變換的速度關系是u‘=u-v,這就意味著:火車系測量的速度等于地面系測量的速度減去火車相對地面的速度。
比如,在速度v=300km/h的高鐵上,如果高鐵系測量列車員的速度u'=5km/h,地面系測量列車員的速度u就應該滿足:5=u-300,u確實等于5+300=305km/h,跟我們的直覺一樣。
但是,我們要清楚地認識到:這些推理都是建立在伽利略變換的基礎上的。
因為我們采用了伽利略變換,所以兩個慣性系之間的速度才可以這樣疊加。火車系測量的速度是5km/h,地面系的結果是300+5=305km/h,這不是什么天經地義的事情,而是伽利略變換的結果。
04牛頓力學的定律
有了這個認識,我們再思考一下:當我們說動量守恒定律是牛頓力學里的定律時,我們到底在說什么?
在牛頓力學里,動量的定義是質量乘以速度,也就是mv。我想看動量守恒定律是不是定律,就是要看在一個慣性系(比如火車系)里成立的動量守恒定律,用伽利略變換把它變到另一個參考系以后,它是否依然成立。
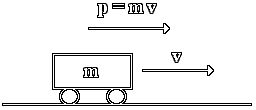
因為質量是一個不變量,不管在哪里都不變。所以,不同慣性系之間動量的差別就體現在速度v上了。
還是以小球的碰撞為例,假設兩個質量都為m的小球以速度v迎面相撞,碰撞后兩個小球黏在一起并保持靜止。取向右的方向為正,從地面系看,碰撞前兩個小球的動量分別為mv和-mv,碰撞前總動量為0。碰撞后,兩個小球黏在一起并保持靜止,所以碰撞后的動量2m×0=0,也是0。
因為碰撞前的總動量等于碰撞后的總動量(都是0),所以,地面系確實認為存在動量守恒定律。
但是,我們看動量守恒定律是不是牛頓力學下的定律,并不是只看這個定律在地面系是否成立,還要看用伽利略變換把它變到另一個慣性系之后,它是否依然成立。
因此,我們要換一個參考系,看看新參考系里的碰撞過程是否依然滿足動量守恒定律。為了計算方便,我們就把新參考系選在從左往右運動的小球身上,也就是站在速度為v的小球上再來看這個問題。
在地面系,兩個小球碰撞前的速度分別為v和-v,碰撞后兩個小球黏在一起,速度為0。那么,在新參考系里,碰撞前后小球的速度又分別是多少呢?
在牛頓力學里,我們使用伽利略變換的速度疊加公式u‘=u-v聯系兩個慣性系之間的速度。也就是說,在原參考系里速度為u的物體,在新參考系里速度就是u‘=u-v。
因此,對于碰撞前速度為v的小球,在新參考里速度為v-v=0;碰撞前速度為-v的小球,在新參考系里速度為-v-v=-2v;碰撞后速度為0的小球,在新參考系里的速度為0-v=-v。
也就是說,同樣的碰撞,新參考系看到的是:兩個質量為m的小球,一個速度為0(以它為參考系,速度當然為0),一個速度為-2v(對面的小球),它們碰撞之后黏在一起,變成了質量為2m,速度為-v的大球。
那么,在新參考系里動量守恒定律還成立么?我們再來驗算一下:碰撞前兩個小球的動量分別為m×0=0和m×(-2v)=-2mv,碰撞后黏在一起的大球的動量為2m×(-v)=-2mv。
看到沒有,新參考系里碰撞前后的動量都是-2mv,依然相等。所以,在新參考系里動量守恒定律依然成立。
當然,這里我們只驗證了一個新參考系。但是,你完全可以根據伽利略變換的速度疊加公式,證明只要把動量定義為mv,動量守恒定律在一般情況下都成立。
這樣,我們才敢理直氣壯地說:如果把動量定義為mv,動量守恒定律的確是牛頓力學里的定律。因為你用伽利略變換把動量守恒定律變到任何慣性系,它都成立。
那么,到了狹義相對論里呢?
05洛倫茲變換
在狹義相對論里,聯系兩個慣性系的不再是伽利略變換,而是全新的洛倫茲變換:
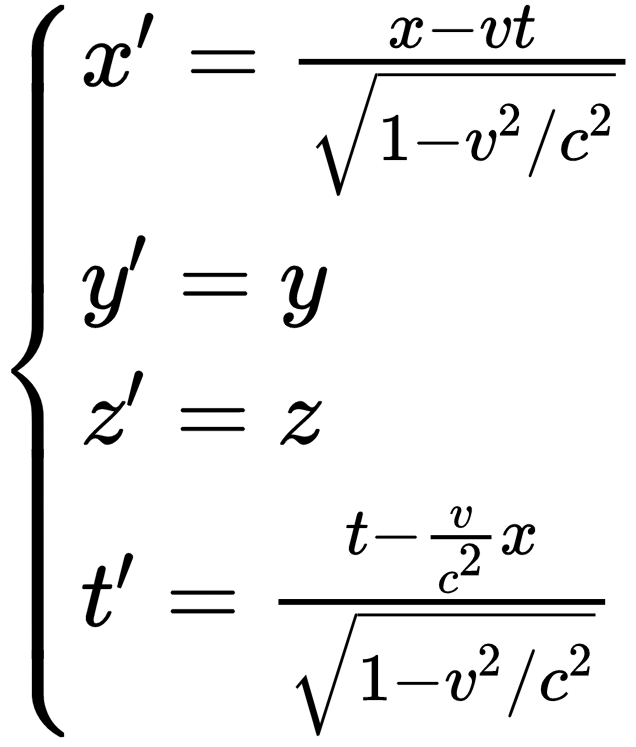
變換的細節我們先不細究,不過你可以看到:在洛倫茲變換里,火車系的時間t'和地面系的時間t不再一樣(t'≠t),它們之間有個巨復雜的關系。
也就是說,在狹義相對論里,時間不再是絕對的,不同慣性系的時間并不一樣,每個慣性系都有自己的時間。
再看看火車系和地面系的x坐標之間的關系,也是一個非常復雜的式子。所以,不難想象,從洛倫茲變換推出的速度疊加公式肯定就沒有伽利略變換的那么簡單。
中間的推導過程我就省了,洛倫茲變換下的速度疊加公式是這樣的:
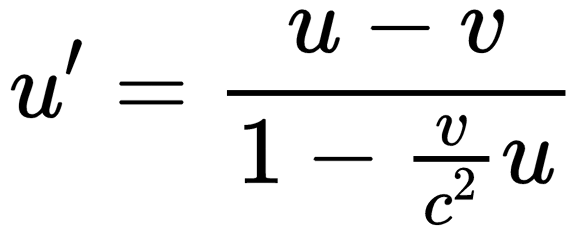
怎么樣,比伽利略變換下的u'=u-v復雜多了吧?
但是,仔細觀察一下就會發現,如果v遠小于光速c,分母的v/c2就約等于0,分母就變成了1,于是這個速度疊加公式就回到了伽利略變換下的u'=u-v。因為牛頓力學是狹義相對論的低速近似,所以伽利略變換自然也是洛倫茲變換的低速近似。
在牛頓力學里,我們使用伽利略變換導出的速度疊加公式,所以可以用300+5=305km/h表示地面系測量的列車員速度。但是,我們在狹義相對論里使用的是洛倫茲變換導出的新速度疊加公式,那結果肯定就不再是305km/h了。
也就是說,如果火車系測量列車員的速度為5km/h,我問地面系的結果是多少?牛頓力學給出的結果是305km/h,這是用伽利略變換算出來的;狹義相對論認為這個結果不等于305km/h(當然也極為接近這個數字),因為它是用洛倫茲變換算出來的。
如果你問誰算得更準確,那當然是狹義相對論的結果更準確,但牛頓力學的結果也跟它極為接近。因為火車的速度v和列車員的速度u都太小了(相對光速c),所以洛倫茲變換的速度疊加公式的分母1-vu/c2基本上等于1,于是基本上就等于伽利略變換的結果。
但是,如果火車的速度接近光速,分母1-vu/c2就會遠小于1,那得到的結果就跟伽利略變換完全不一樣了,所以牛頓力學就不能用了。
通過這個例子,相信大家對伽利略變換和洛倫茲變換都有了一定的了解,也明白不同變換下的速度疊加公式是不一樣的。具體的計算過程可以不用搞得太清楚(親自推一遍當然更好),但道理一定要明白。
06狹義相對論的定律
知道了洛倫茲變換,我們再來看這個問題:在狹義相對論里,動量守恒定律還是定律嗎?
當我們在說這句話的時候,我們的意思是:如果把動量仍然定義為mv,那動量守恒定律在洛倫茲變換下還能保持數學形式不變么?如果動量守恒定律在一個慣性系里成立,我用洛倫茲變換把它變到另一個慣性系以后,它還成立嗎?
具體的計算我就不做了,稍微想一下就知道答案肯定是否定的。
因為我們已經證明了:如果把動量定義為mv,動量守恒定律在伽利略變換下是可以保持數學形式不變的,這樣動量守恒定律才步入了牛頓力學的殿堂。
然而,現在動量的定義(mv)沒變,聯系兩個慣性系之間的變換卻從伽利略變換變成了洛倫茲變換。既然伽利略變換能讓動量守恒定律保持數學形式不變,那換了變換以后肯定就不一樣了啊。
也就是說,如果我們依然把動量定義為mv,在洛倫茲變換下,新參考系的動量守恒定律必然不再成立。
要驗算也很簡單,洛倫茲變換下的速度疊加公式是這樣的:
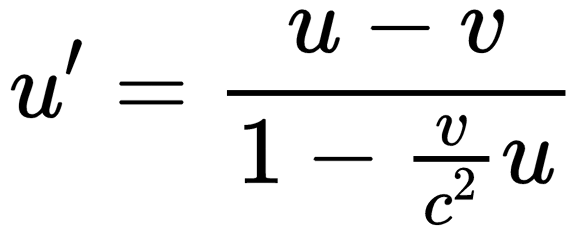
還是剛才的小球碰撞問題,我們可以用同樣的方法把新舊慣性系碰撞前后的速度都算出來,再看看動量是否相等。
誰算誰知道,答案必然不相等。
于是,我們就面臨一個非常棘手的問題:如果我們在狹義相對論里依然把動量定義為mv,那么,經過洛倫茲變換以后,新參考系里的動量守恒定律就不再成立。如果動量守恒定律無法在洛倫茲變換下保持數學形式不變,那它就沒有資格成為狹義相對論里的定律。
也就是說,如果我們繼續沿用牛頓力學的動量定義(mv),那狹義相對論里動量守恒定律就不再成立。
怎么辦?
解決方案也很明顯:要么,我們放棄動量守恒定律,認為狹義相對論里動量守恒定律不再成立;要么,我們修改一下動量的定義,讓新定義下的動量守恒定律在洛倫茲變換下依然可以保持數學形式不變,從而保住它在狹義相對論里的定律地位。
很顯然,閉著眼睛我們都知道要選后者。
動量守恒定律這么重要的東西,你說放棄就放棄了?為了堅持動量的定義(mv)而放棄動量守恒定律,這種行為太愚蠢了。如果動量守恒定律不再成立,我要動量有何用?
07新的動量
所以,為了保住狹義相對論里的動量守恒定律,我們需要重新定義動量。重新定義的目的,就是讓新的動量守恒定律具有洛倫茲協變性,讓它在狹義相對論里能繼續以定律自居。
那么,我們要把新動量定義成啥樣,才能讓它具有洛倫茲協變性呢?這個倒不難,因為洛倫茲變換是明確給出了的,我們只要湊出一個新動量,讓動量守恒定律在洛倫茲變換下依然可以保持數學形式不變,而且在速度遠小于光速時能夠回到牛頓力學的定義就行了。
這個過程我略了,感興趣的自己去試一下。最后,為了保住狹義相對論里的動量守恒定律,我們必須把動量定義成這樣:
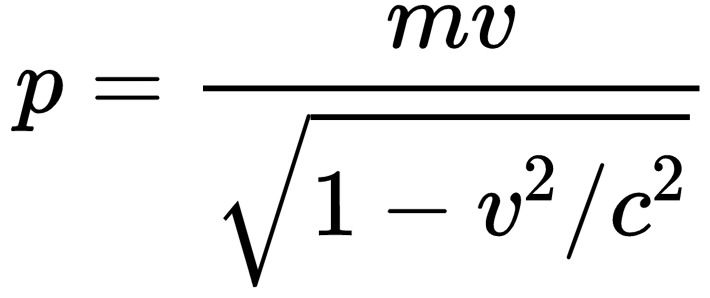
可以看到,當v遠小于光速c時,分母就會變成1,此時的動量就回到了牛頓力學的定義mv。而且,你試一試,這樣定義動量,確實可以讓動量守恒定律在洛倫茲變換下保持數學形式不變,皆大歡喜。
到這里,我們就完成了從牛頓力學到相對論力學升級的第一步。為了讓動量守恒定律具有洛倫茲協變性,我們修改了動量的定義。
但是,力學量又不止動量一個,物理定律也不止動量守恒定律一個。你考慮了動量守恒定律,那能量守恒定律要不要考慮?你改了動量的定義,那動能的定義要不要改?
改,當然要改,一個個排隊慢慢來!
為了讓動能不跟新的動量發生矛盾,為了讓能量守恒定律也能順利入駐狹義相對論,我們需要同步修改動能的定義。
而接下來,就是見證奇跡的時刻:一旦開始修改動能的定義,你會發現質能方程E=mc2竟然神奇地冒出來了。
08新的動能
狹義相對論里的動能要怎么改呢?當然是照著牛頓力學慢慢改。
在牛頓力學里,動能的定義是mv2/2。一個質量為m的木塊靜止在地面,它的動能為0,我用一個恒力F推這個木塊,木塊移動了距離S,速度均勻加速到了v。
我在《什么是高中物理?》的第25節跟大家算過:一個物體在恒力F的作用下會以一定的加速度做勻加速運動。根據牛頓第二定律,這個力F和物體的質量m以及加速度a之間的關系是:F=ma。而一個物體以加速度a從0加速到v,運動的距離S可以表示成:S=v2/2a。
如果我們算一下力F在空間上的累積(也就是力F做的功)F·S,會發現它剛好就等于物體增加的動能mv2/2:
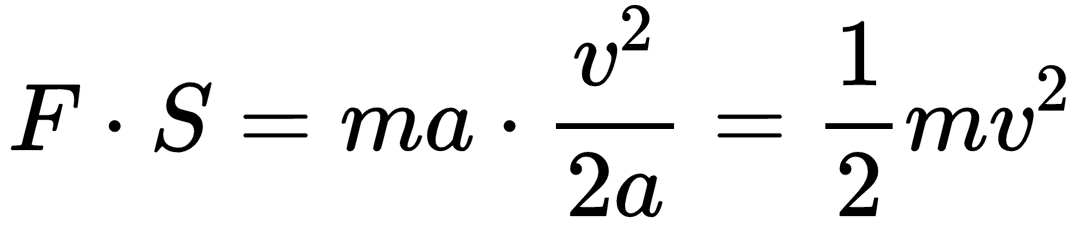
也就是說,合外力對物體做的功等于動能的改變量,這就是中學的動能定理。也因如此,我們在牛頓力學里可以用合外力F和位移S的乘積F·S來表示動能增加的大小,如果物體一開始動能為0,那F·S就是物體最終的動能。
那么,牛頓力學里這個關于動能的計算方式可不可以搬到狹義相對論里來呢?
大抵還是可以的,畢竟狹義相對論在低速情況下還要回到牛頓力學,所以許多東西都會保持一定的一致性。比如,狹義相對論里的動量雖然不再是mv,但是基本形式上還是質量m乘以速度v,只不過加了一個相對論特有的系數。
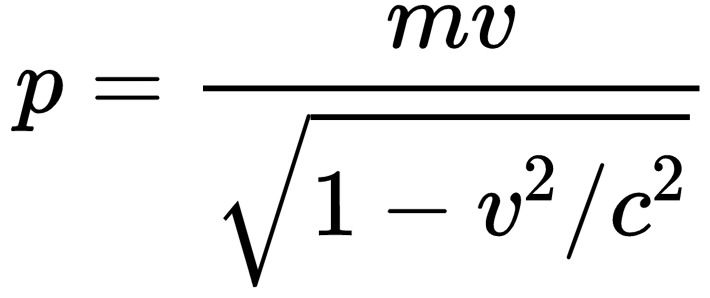
因此,我們在狹義相對論里就暫時用F·S計算動能好了。位移S好說,但問題是:這個力F要如何表示?
在牛頓力學里,力F的常見表示有兩種:一種是根據牛頓第二定律F=ma來算;另一種是對F=ma做一個微小的變形,把加速度a按照定義表示成Δv/Δt,然后把m和Δv組合成動量的改變量Δp(p=mv),然后F=ma=mΔv/Δt=Δp/Δt。
也就是說,對于力F,我們既可以把它表示成質量m和加速度a的乘積,也可以把它表示成單位時間內動量的變化量,也就是動量的變化率Δp/Δt。然而,狹義相對論里的新動量我們已經找到了,那就直接用動量的變化率Δp/Δt表示F,再用F·S計算物體的動能吧,省時省力。
然后,我們要意識到一件事:前面我們都假設力F是恒力,認為物體在做勻加速運動,這是一種特例。
我們要計算物體的動能,要推導質能方程,當然不希望它只在這種特殊情況下才成立。所以,我們要考慮更一般的情況:如果力F和位移S都在變,我們應該如何計算它們的乘積?
地球的表面是彎的,但在小范圍內我們可以認為它是平的。同理,在足夠小的范圍內,我一樣可以認為力F和位移S的大小不變。如果用ds表示這個微小的位移變化,用F·ds表示力F在這個微小位移里做的功,那么,把0到S所有的功累加起來就能得到總動能E。
寫成數學表達式就是這樣:
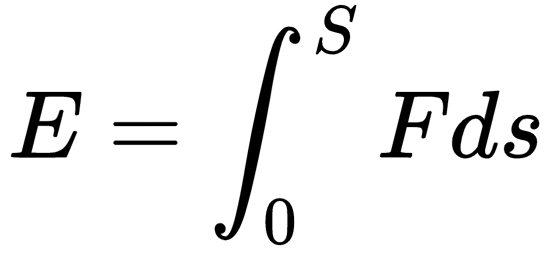
很顯然,為了保證結果的一般性,我們這里動用了微積分。這個具體的計算過程我不想多講,因為但凡學了微積分,會分部積分的同學都知道怎么算。如果你不會微積分,這個計算過程我也沒法在這里給你科普,我只能建議你先看看我的《你也能懂的微積分》,再找本微積分教材看看。
更為重要的是:這個計算過程并不會影響你對質能方程的理解。
因為這只是一個純數學計算手段。人們之所以誤解質能方程,并不是因為不知道這個公式的形式是E=mc2,而是無法理解這個方程背后的物理意義和物理背景。
如果你跟著我的思路來到這里,知道為了讓動量守恒定律滿足洛倫茲協變性,我們不得不重新定義了動量,進而需要重新定義動能。你就會知道質能方程到底是怎么來的,就算看不懂中間的計算過程,也不會影響你對質能方程的理解。
這里,我就放一張新動能的推導圖片,你能看懂就看,看不懂也沒事。當然,如果你暫時看不懂,但是為了能看懂而去學習微積分,那自然是極好的。這里也沒多少微積分的知識,關鍵就是一個分部積分。計算思路也非常簡單,就是用狹義相對論里新動量的變化率代替力F:
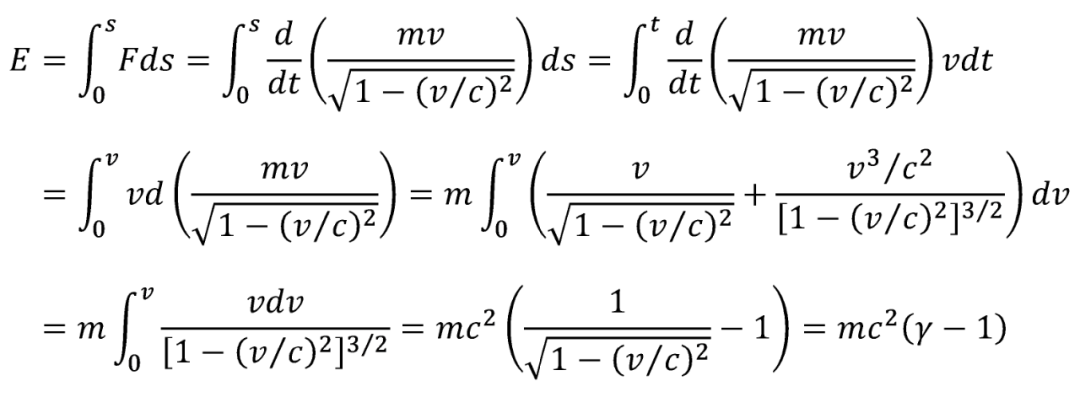
我把結果放到倒數第二步:
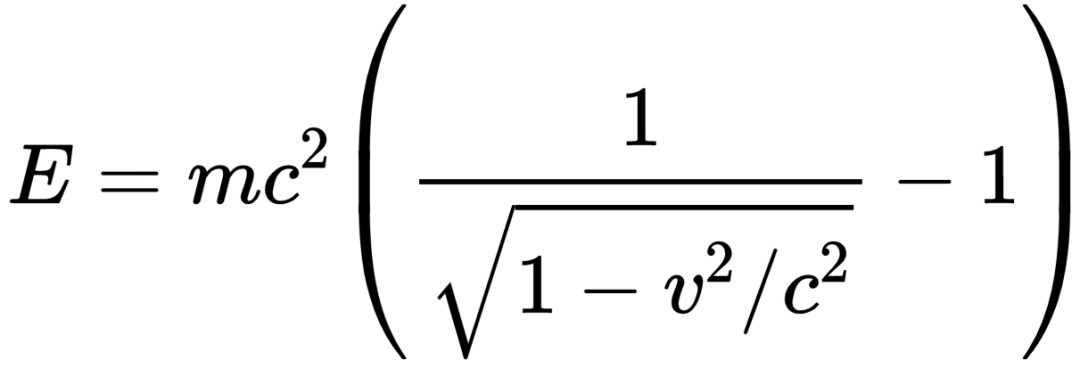
也就是說,一個物體的動能E在狹義相對論里可以表示成這樣:括號外面是mc2,括號里面是相對論因子減去1。
我們把中間那一大串東西稱為相對論因子(也叫洛倫茲因子),因為相對論里經常會用到它,所以我們就用一個特殊符號γ來表示這個相對論因子:
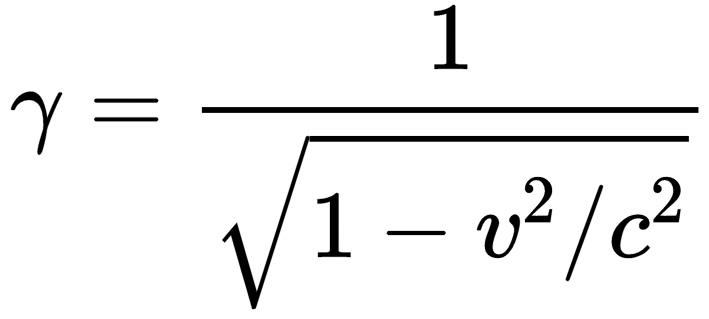
這樣,你再看看狹義相對論里的新動量,是不是就相當于在牛頓力學的動量mv上乘了一個相對論因子γ?也就是說,狹義相對論里的新動量可以簡寫成p=γmv。
同樣,上面的動能表達式一樣可以通過相對論因子γ簡寫為:
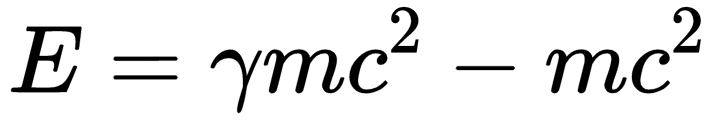
在這個式子里,m依然是我們熟知的質量,是一個不隨速度和參考系變化而變化的物理量。而這個E,就是因為有力F作用在物體身上,物體因為運動而具有的動能。
這個動能的形式很有意思。
在牛頓力學里,動能的表達式是mv2/2,只有一項;到了狹義相對論,動能的表達式竟然有兩項。而且,后一項mc2竟然跟物體的速度v沒有關系,只跟物體的質量m有關,只有前一項γmc2才會隨著速度的增大而增大(因為γ會隨著速度的變大而變大)。
這有點拔出蘿卜帶出泥的味道,原本我們只是在正正經經地計算狹義相對論的新動能。現在你倒好,你算出的新動能里竟然還有一項跟速度無關的mc2,單位還跟能量一樣。
仔細看看這個新動能,如果物體的速度v為0,相對論因子γ就等于1,那動能就變成了E=mc2-mc2=0。靜止物體的動能為0,很符合我們對動能的認知。
如果物體的速度開始增大,相對論因子γ就開始大于1,第一項γmc2就在增大,它跟mc2的差值也會不斷增大,結果就是動能不斷增大。
這給人的感覺,就好像是物體靜止時具有mc2的能量,當物體開始運動時,我們用γmc2減去物體靜止時具有的能量mc2就得到了物體的動能。所以,愛因斯坦面對這個式子時,創造性地把mc2解釋為質量為m的物體靜止時具有的能量,簡稱靜能。
如果我們把mc2解釋為物體的靜能,而E是物體的動能,那靜能+動能自然就是物體具有的總能量。于是,γmc2就成了物體具有的總能量(動能+靜能)。
這樣解釋的話,是不是一切都合情合理了呢?
09質能方程
復盤整個過程,我們到底做了什么?
我們只是堅持狹義相對論的基本原理,認為物理定律在洛倫茲變換下應該保持數學形式不變,也就是認為物理定律應該具有洛倫茲協變性。
然后,為了讓動量守恒定律具有洛倫茲協變性,我們修改了動量的定義。動量修改了以后,動能自然也得跟著改。然而,令誰也沒有想到的是:當我們把這種符合狹義相對論精神的新動能(E=γmc2-mc2)計算出來以后,發現它竟然帶了一個尾巴mc2。
接著,愛因斯坦認為mc2應該是物體靜止時具有的能量,也就是靜能,γmc2是物體的靜能和動能之和,也就是物體的總能量。
整個過程,我們唯一引入的就是狹義相對論的基本原理,也就是認為物理定律應該具有洛倫茲協變性,然后就發現狹義相對論的新動能把靜能mc2帶出來了,這太意外了!
于是,我們就從狹義相對論里自然而然地推出了質能方程:E=mc2。
不知道愛因斯坦看到這個結論后是什么反應,這只是牛頓力學向相對論力學升級過程中的一個小步驟,結果卻發現能量和質量之間竟然有E=mc2這樣一種神奇的關系。
這個結論看起來是如此的不可思議,因為真空光速c是一個非常大的數字(3×10^8m/s),平方一下就更大了。根據質能方程,一個半斤重的蘋果蘊含的能量將高達525萬噸TNT當量,大致相當于350顆廣島原子彈爆炸釋放的能量,這太夸張了。
但是,E=mc2又是直接從狹義相對論的基本原理直接推出來的,如果質能方程錯了,那就是狹義相對論錯了。而愛因斯坦對狹義相對論的信心是極強的,所以,他在寫完《論動體的電動力學》的三個月后,就完成了質能方程的論文。
10回到牛頓
習慣了將動能視為mv2/2的人可能不太習慣E=γmc2-mc2這種新動能表達式。但是,因為牛頓力學是狹義相對論的低速近似,所以它在低速條件下依然可以回到大家熟悉的mv2/2,不信我們來試一試。
把相對論因子γ進行泰勒展開,就得到了這樣的結果:
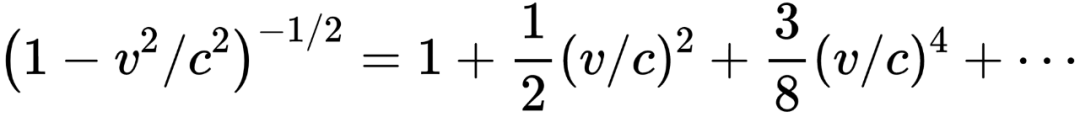
泰勒展開就是看你想近似到什么程度,你不是說牛頓力學是相對論力學的低速近似么?那相對論力學要低速近似到什么程度才會變成牛頓力學呢?泰勒展開會告訴我們答案。
如上圖,我們對一張真實照片進行了“泰勒展開”。一階近似下就是隨便描了一個輪廓,我們可能看了個寂寞;二階近似下可以看清楚一些細節,圖片變清楚了一些;三階近似下,細節就更清楚了,更接近原圖……
只要你開心,你可以無限階近似下去,近似的階數越高,圖片就越接近原始圖片。同理,我們對相對論因子γ進行泰勒展開,它就被分成了無窮多項的疊加,你可以按照自己的需求采取相應的近似水平。
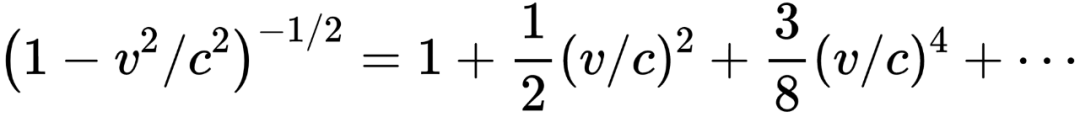
我們說牛頓力學是相對論力學的低速近似,這個低速是相對于光速而言的。當速度v遠小于光速c時,v/c就是一項很小的項,(v/c)2以及更高次項就是更小的項了,可以選擇性忽略。
那么,如果我們只取前兩項,也就是取γ=1+(v/c)2/2,再把γ代入狹義相對論的新動能:E=γmc2-mc2=mc2(γ-1)=mv2/2。不多不少,剛好就回到了牛頓力學的mv2/2。
也就是說,牛頓力學的動能只是狹義相對論動能的一個二階近似。
因為mv2/2只是一個近似值,所以它必然會丟失一些信息。只是,萬萬沒想到,它丟失的信息里居然包含了物體靜止時具有的能量mc2。一旦我們通過更加精確的狹義相對論把這個丟失的信息找了回來,就會發現任何質量為m的物體都含有mc2如此巨大的能量。
其實,靜止的物體具有能量一點也不奇怪。
一堆火藥放在那里,你肯定知道它有能量,甚至能算出這堆火藥爆炸時會釋放出多少能量。與此同時,你也知道火藥爆炸釋放的只是部分化學能,并不是它的全部能量。現在,我們第一次有辦法把它的全部能量算出來了,途徑就是質能方程E=mc2。
質能方程把質量和能量聯系起來了。那么,在這種新視角下,我們應該如何看待質量和能量的關系呢?
11質量與能量
再次回到狹義相對論的動能表達式:
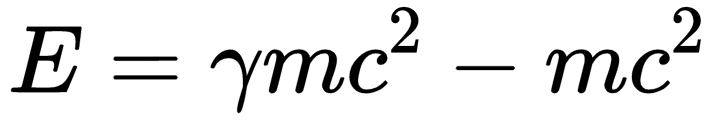
回想一下,愛因斯坦是如何解釋這個式子的?愛因斯坦想:既然E是物體的動能,那么γmc2就是物體的總能量,mc2是物體靜止時具有的能量,簡稱靜能。
注意,我們是先得到了動能E,是先有能量,先有總能量γmc2和靜能mc2,然后再考慮如何衡量能量的大小。因為c是常數,所以就只能用質量m來衡量靜能的大小,這個次序不能亂。
于是乎,質量就成了能量的量度。
因此,如果物體吸收了一點能量,它靜止時的能量增加了,質量也會增加;如果物體釋放了一點能量,它靜止時的能量減少了,質量也會減小。
所以,把質能方程寫成m=E/c2反而更容易理解它的含義(愛因斯坦一開始就是這么寫的):你想知道一個物體的質量是多少嗎?那就用它靜止時的能量除以c2吧,于是我們才說質量是能量的量度。
一個物體靜止時的能量是多種多樣的,可以有內能、化學能、核能以及各種勢能。但是我不關心種類,你把它們都加起來,除以c2就能得到物體的質量m。
為什么我要如此小心翼翼地描述這一段呢?因為只有極少數人在看到質能方程E=mc2后會認為它是在說“質量是能量的量度”,許多人的第一反應是:質能方程意味著“質量可以轉化成能量”。核反應里出現了質量虧損,就是一塊“實實在在”的物質丟失了一塊質量,然后它們轉化成了“虛無縹緲”的能量。
這是一種非常常見,但危害極大的誤解。順著這種誤解,稍微發散一下就能搞出太極相對論、佛學相對論之類的東西。你以為原子彈釋放了能量,是因為原子彈爆炸時丟失了一塊東西,然后這部分質量轉化成了能量?
不不不,原子彈爆炸釋放能量的過程,跟一般的火藥爆炸沒什么不同,只不過前者釋放的能量比較多,后者釋放的能量比較少而已。原子彈爆炸釋放了能量,所以度量原子彈能量的質量會減少;火藥爆炸釋放了能量,所以度量火藥能量的質量也會減少。
這就是一個普通的能量轉化過程,體系的一部分能量(原子彈的核能,火藥的化學能等)通過爆炸轉化成了動能和其它能量。于是,原子彈和火藥的能量E減少了,度量這個能量的質量m也相應減少了,并且遵守E=mc2,僅此而已。
這也是我比較討厭“質量虧損”這個詞的原因,它太容易讓人誤解了,太容易讓人誤以為質量只在核反應中才會減少,讓人誤以為核反應就是“質量轉化成了能量”。
沒有什么質量轉化成了能量,只有質量是能量的量度,質量就是度量一個物體靜止時具有多少能量的。
我知道,不管我在這里說什么,你都難以接受為什么我們不能說“質量轉化成了能量”,你不認為這樣有什么不妥,甚至覺得它理所當然。而且,就算我讓你強行記住這個結論,你后面還是會忘的,畢竟大家都習慣用自己習慣的方式思考。
所以,我們就來深入地扒一扒,看看你在說“質量轉化成能量”時,你到底在說什么?看看為什么很多人會這樣想,以及最重要的:為什么質能方程E=mc2不能這么理解?
12牛頓的質量
在牛頓時代,大家認為宇宙萬物都是由微小的實物粒子(原子)組成,認為宇宙就是一堆粒子的集合,各種物理現象只是粒子間的排列組合和運動變化,而粒子的運動規律則由牛頓力學給出。
在這樣的語境下,人們認為組成物質的基本微粒是不可摧毀的,自然界的各種變化只是它們的排列組合,并不會摧毀粒子本身。到了18世紀,化學家們在一定精度內發現化學反應前后物質的總質量不變,也就是大名鼎鼎的質量守恒定律,這就更加佐證了這種觀點。
因為化學反應只是原子間的排列組合,如果原子的種類和數目都沒變,那原子的總質量就不變,質量自然就守恒了。
一旦我們認為“一個物體的質量等于組成這個物體的所有微粒質量之和”,質量基本上就被當成了物質的代名詞。因為,你潛意識里會覺得:只要是物質,肯定就由一些實物微粒組成,它的質量自然就等于所有微粒的質量之和。
那能量呢,能量在這種語境下又扮演了什么角色?
還是看化學反應,我們認為化學反應就是原子間的排列組合。比如木炭燃燒,在化學家眼里就是木炭里的碳原子和空氣中的氧原子重新組成了二氧化碳分子,這個過程釋放了能量,但燃燒前后原子的種類和數量都沒變,所以質量不變。
也就是說,化學家認為雖然木炭燃燒釋放了能量,但它們的質量不會變。在這種語境下,質量和能量明顯是不同的東西:質量是組成物質的所有原子質量之和,能量不過是原子在重組過程中釋放出來的副產品。
正因為牛頓語境下的質量和能量是如此的不同,我們在第一次看到質能方程E=mc2,第一次聽說在核反應里會發生違反質量守恒定律的“質量虧損”時,才會認為這是“質量轉化成了能量”,是組成物質的實物粒子實實在在地被摧毀了(質量減小),然后神奇地轉化成了能量。
但問題是,質能方程E=mc2并不是牛頓力學的東西,而是狹義相對論的天之驕子啊。
相對論和量子力學是20世紀物理學的兩大革命,它們顛覆了牛頓力學的許多觀念。物質不能再簡單地看作一堆實物粒子的集合,質量不再是組成物體粒子的質量之和,化學家發現的質量守恒定律也不再成立……
總之就是,時代變了,世界變了,一切都變了,原來的“質量轉化成能量”自然也得跟著變。所以,如果我們想搞清楚為什么不能再那樣思考,就得先搞清楚牛頓的觀念是如何被打破的?
13電磁場的挑戰
狹義相對論是愛因斯坦在協調電磁理論和牛頓力學的過程中建立起來的,所以它的論文就叫《論動體的電動力學》(公眾號后臺回復“狹義相對論論文”獲取原論文)。
我們也知道,在19世紀建立電磁大廈的過程中,有兩個人的作用至關重要,他們是法拉第和麥克斯韋。
法拉第創造性地提出了“場”,用電磁場來描述電磁現象。麥克斯韋則用優美的數學語言把法拉第的思想表現了出來,得到了能夠描述一切經典電磁現象的麥克斯韋方程組。
這些歷史大家都很熟悉,但是很多人沒有注意到:法拉第提出的電磁場,其實是一個超出牛頓物理圖景的概念。
什么意思?在牛頓的觀念里,物質是由基本微粒組成的,那電磁場是由什么微粒組成的呢?很顯然,電磁場并不由什么微粒組成,這看起來就跟牛頓的物質觀發生了沖突。
于是,有些人就主張電磁場只是描述物質的一種數學手段,不具有物理上的意義,也就是不認為電磁場是真實的物質,這樣牛頓的物質觀就不用對它負責了。但是,很快人們就發現不能這么干,因為電磁場具有能量。
為什么電磁場具有能量呢?
舉個例子,我從北京向武漢發射一束電磁波,因為電磁波的速度有限(光速),它從北京到武漢需要一段時間。那么,當電磁波離開了北京,卻又還沒到武漢時,能量去哪了?此時的能量既不在北京,也不在武漢,那就只能在電磁場里。
于是乎,電磁場就理所當然具有了能量。一個東西具有能量,那它肯定就有物理上的意義,也就是說它是真實存在的物質。如果電磁場是物質,而它又不由實物微粒構成,那就真的跟牛頓的觀念沖突了。
但人們還不死心,雖然電磁場是真實存在的物質,但我們還是可以把電磁場和電磁波看作某種實物粒子衍生出來的現象,這樣它們的基礎就還是牛頓的實物粒子。
比如水波,雖然它是真實存在的,但水波其實是許多水分子有規律的運動衍生出來的現象,它的基礎還是水分子這種“微粒”。那么,如果我們認為電磁波跟水波一樣,也是由于某種微粒的振動引起的,這不就符合牛頓的觀念了么?
按理說,這種想法是非常自然的,畢竟水波、電磁波都是波。但問題是,當我們說水波是由水分子的振動引起時,我們的確看見了水,所以說“水是水波的介質”沒什么問題。
但如果你說電磁波也是由某種介質的振動引起的,那這種介質是什么?光就一種電磁波,光可以在太空、真空中傳播,而這里似乎什么都沒有,不存在什么介質。你總不能說電磁波是由某種介質的振動引起的,但又說不出這種介質是什么吧?
是,電磁波的確有可能存在介質,只是我們還沒發現,沒發現并不代表它不存在。但是,你也要明白這么做的巨大風險:這是在假設一種看不見、摸不著,目前任何實驗都觀測不到,卻又在太空、真空中廣泛存在的介質。
雖然一聽就不怎么靠譜,但想到只有這樣才能不違背牛頓的觀念,人們(包括麥克斯韋、赫茲)就紛紛接受了,并將這種介質命名為以太。也就是說,如果我們把電磁波看作以太的振動,就像把水波看作水的振動那樣,它就可以與牛頓的觀念和平共處了。
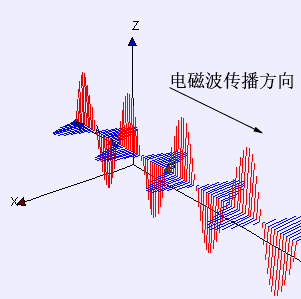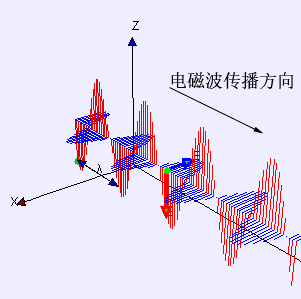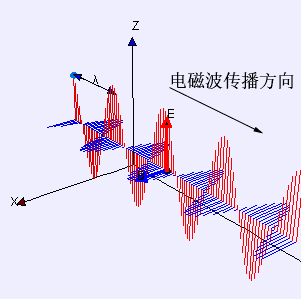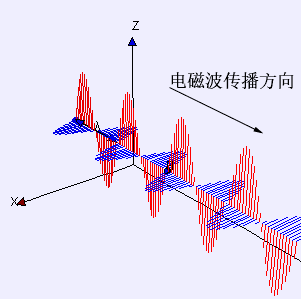
然而,我們都知道愛因斯坦在狹義相對論里把以太仍了,也就是把作為電磁波介質的以太仍了。他認為并不能把電磁波看作以太的振動,電磁波不需要介質,它跟水波有本質的區別。
那有人就要問了:如果電磁波沒有介質,它是怎么傳播出去的呢?
我反倒想問一句:你憑什么覺得只要是波,就一定要有介質呢?你覺得水波、聲波都是通過介質傳出去的,所以電磁波也要有介質?
沒道理啊,沒理由說張三李四是這樣,就要求王五也這樣。更重要的是,你認為波都有介質,其實就是認為所有的波都跟水波一樣,都是通過相鄰介質點的力學作用傳出去的。但我們已經說了電磁波跟水波不一樣,那就不能套這個邏輯了,更多細節可以看看我的《相對論誕生:愛因斯坦是如何創立狹義相對論的?| 主線》。
因此,到了狹義相對論,我們是徹底無法再把電磁波當作某種介質(以太)的振動了,無法再把它還原為某種微粒的衍生現象了,這就跟牛頓的物理圖景徹底沖突了。
于是,我們現在就有兩種東西:一種是實物微粒,比如分子、原子、質子、中子等,它們看上去可以由更基本的微粒組成;另一種就是無法看成實物微粒的電磁場。
如何把它們統一起來呢?
很顯然,牛頓力學是辦不到的,我們需要狹義相對論和量子力學才能統一它們。這種包含了狹義相對論、量子力學以及場論思想的全新理論,就叫量子場論。這是一種全新的物理圖景,大家熟悉的粒子物理標準模型就是在這上面建立起來的。
怎么統一實物粒子和場呢?無非就是兩種思路:要么認為粒子更基本,場是粒子的某種衍生物(牛頓物理干不了這事,現代物理學里倒是有人這么考慮,比如溫伯格);要么就認為場更基本,粒子是場的某種衍生物。
量子場論的主流思想是后一種,也就是認為場更加基本,粒子只是場的激發態。比如,電磁場是更基本的,電磁場的激發態就是光子;質子場是更基本的,質子場的激發態就是質子,以此類推。
量子場論認為萬物皆場,場是更加基本的東西。粒子只是這種量子化場的激發態,場與場之間的相互作用決定了要發生的一切。具體細節這里就不多說了,后面科普量子力學時再細說。
總之,到這里大家就應該清楚了:牛頓的物理圖景已經崩塌了,物質并不是由堅不可摧的實物粒子組成的。在更現代的量子場論里,場反而是更加基本的東西,粒子只是場的激發態。
如果你記住了這一點,質能方程E=mc2就非常容易理解了。因為質能方程最難以理解的地方,就是你非要用牛頓的觀念,來理解這個已經完全超出了牛頓物理學的東西。
量子場論是狹義相對論和量子力學聯姻的產物,因此必然能跟質能方程相容。我這里并不要求你理解量子場論,只要你能意識到不能再用牛頓的觀念來思考質能方程,后面的一切就都好說了
打了這樣的預防針,我們再來看看經常跟質能方程同時出現的質量虧損。
14質量虧損
進入20世紀,人們發現了一件“奇怪”的事情:組成原子核的核子質量之和,竟然比原子核本身的質量要大。
什么意思?我們知道原子核是由質子和中子組成的,比如氘核就是由一個質子和一個中子組成。按照原來的觀念,我們肯定認為氘核的質量等于一個質子的質量加上一個中子的質量。但實驗結果卻是:一個質子和一個中子的質量之和比氘核的質量要大。
為什么?
我們對這個結果表示驚奇,是因為它跟牛頓的觀念不一樣。我們認為一個物體的質量應該等于所有組成物體的微粒質量之和,認為一個氘核的質量應該等于一個質子加上一個中子的質量。但結果卻是一個質子(1.6726×10^-27kg)和一個中子(1.6749×10^-27kg)的質量之和(3.3475×10^-27kg)比一個氘核(3.3436×10^-27kg)的質量要大。
而且,我們還知道:質子和中子結合成氘核釋放的能量E,跟減少的質量m之間剛好滿足E=mc2。
于是,很多地方就用質量虧損來解釋這個事,說質子和中子組合成氘核時發生了質量虧損,虧損的質量就按質能方程釋放能量。
從牛頓的觀念來看,這樣考慮是非常自然的。因為質量減小了,肯定就意味著損失了一部分組成物質的“真材實料”,而它剛好又按照質能方程釋放了一定的能量,這可不就是損失的質量轉化成了能量么?
但問題是,質能方程是狹義相對論的產物,我們不能再用牛頓的觀念去思考,因而不能說是“質量轉化成了能量”。
那問題到底出在哪?我們應該如何看待質子和中子結合成氘核這個現象?如果不是核原料損失了一部分質量并轉化成了能量,那又是什么呢?
問題的關鍵就在于:單獨的質子是質子,跟中子一起組成氘核的質子還是質子,它們并沒有什么不同。既然質子的成分都是一樣的(兩個上夸克和一個下夸克組成),并沒有在跟中子組合成氘核的過程中損失什么,你說它質量虧損到底是虧損了什么?
是原來的質子由三個夸克組成,組成氘核之后的質子就損失了一個夸克,只由兩個夸克組成了?或者是,你覺得原來的質子是由100個什么微粒組成的,組成氘核的質子就損失了1個微粒,只有99個微粒了?
顯然,不可能是這樣。質子有質子的內部結構,如果它的內部結構發生了變化,那就不是質子了。就像一個質子和一個中子組成了氘核,但如果增加了一個中子,那就不叫氘核,而是氚核。
既然單獨的質子叫質子,氘核里的質子也叫質子,那它們就應該是一樣的,質子并沒有缺胳膊少腿,中子也一樣。既然質子和中子都沒有損失什么成分,那它們質量虧損到底是虧損了什么呢?它又能虧損什么呢?
出問題了吧?仔細一推敲,你就會發現這個邏輯是行不通的。
但是,在核反應里確實發生了質量虧損啊。質子、中子和氘核的質量都能查到,確實是前兩者加起來比后者大,質量確實損失了一部分啊,這到底是怎么回事呢?
大家認為化學反應前后質量守恒,認為兩塊磚頭一起稱的質量應該等于單獨稱的質量之和,為什么質子和中子組成氘核之后質量就減少了呢?難道核反應比較特殊,有它獨特的規律?
15核反應特殊嗎?
核反應它一點也不特殊!
質子和中子組合成氘核,它是核子(組成原子核的粒子,包括質子、中子以及它們的反粒子)的重新組合,化學反應是原子的重新組合。一個是核子的重組,一個是原子的重組,有什么本質的區別?
核子間的相互作用主要是強力,原子間的相互作用主要是電磁力,除了強力比電磁力要強一些以外,核反應和化學反應沒什么太大的不同。
甚至,兩塊磁鐵在磁力作用下吸在了一起,這個過程跟核反應、化學反應也沒什么本質的區別,無非就是把核子、原子換成了磁鐵,是不是這個道理?
如果核反應沒什么特殊,那質子和中子組成氘核釋放出能量,碳原子和氧原子組成二氧化碳分子(木炭燃燒)釋放出能量,兩塊磁鐵吸在一起釋放出能量(沒錯,的確釋放了能量,不然磁鐵碰撞時的聲音是哪來的?)的過程就應該是類似的。
如果質子和中子組成氘核的核反應會發生質量虧損,那木炭燃燒會不會發生質量虧損?兩個磁鐵吸在一起會不會發生質量虧損?
有些人可能有點懵,因為他印象里的“質量虧損”是一個非常高級的名詞,是一個違背了質量守恒定律的東西。這種反直覺的新玩意,只有全新的相對論與核反應才能與之相配,一般的化學反應怎配享有如此待遇?把兩個磁鐵放到這里來就更過分了。
而且,中學化學也講過,化學反應前后物質的總質量是不變的。兩個磁鐵吸在一起,根據直覺,前后的質量就更加不可能變了。所以,根據直覺和常識,他絕不相信化學反應、磁鐵吸在一起也會發生質量虧損。
但是,我上面的推理也很有道理啊,核反應也好,化學反應、磁鐵吸在一起也好,都是兩個小東西組成了一個大東西,并且都釋放了能量。區別無非就是核反應釋放的能量大,化學反應釋放的能量中等,磁鐵吸在一起釋放的能量少,并沒有什么本質的不同。
還有,質能方程E=mc2是愛因斯坦從狹義相對論的基本原理推出來的,所以,狹義相對論成立的地方質能方程也應該成立。那么,狹義相對論就只在核反應里成立?化學反應和磁鐵相吸就不遵守狹義相對論了么?顯然不是啊。
因此,從直覺和常識出發,我們覺得只有核反應才會發生質量虧損,虧損的質量和釋放的能量滿足質能方程。從邏輯和推理出發,又似乎是核反應、化學反應、磁鐵吸在一起的過程都會出現質量虧損,虧損的質量跟釋放的能量之間都滿足質能方程。
直覺和邏輯發生了沖突,我聽誰的?
當然是邏輯,科學從來就不是為了符合你的直覺而建立的。你要說直覺,亞里士多德的理論最符合直覺了,牛頓的都很反直覺,更別說相對論了。
所以,我們應該相信核反應、化學反應、磁鐵吸在一起的過程中都發生了質量虧損。
如果化學反應也有質量虧損,那虧損的質量m跟化學反應(比如木炭燃燒)釋放的能量E之間也會滿足E=mc2。只不過,化學反應釋放的能量E比較少,而光速c又很大,所以根據E/c2算出來的虧損質量m就非常小,小到平常根本察覺不出來,于是化學家們才總結出了質量守恒定律。
至于磁鐵,它們吸在一起時釋放的能量就更少了,虧損的質量也就更小。所以,我們就更加不會察覺分開的磁鐵與吸在一起的磁鐵在質量上會有什么不同了。
這樣,我們就能以一種統一的邏輯解釋所有的事情,既不與理論相沖突(從狹義相對論推出的E=mc2是普適的,核反應、化學反應、磁鐵都應該遵守),也不跟實驗相沖突(核反應容易觀測到,化學反應、磁鐵不太容易觀測到)。
那問題的關鍵就來了:如果這種邏輯是對的,如果核反應、化學反應甚至磁鐵吸在一起釋放能量時都發生了質量虧損,而我們又不能像牛頓那樣認為是組成物質的“材料”少了一塊,那它到底虧損了什么?為什么它的質量會減少?
這就涉及到一個非常關鍵問題:在狹義相對論里,我們應該如何看待質量?
16質量是能量的量度
木炭燃燒時,碳原子和氧原子結合成二氧化碳分子,這個過程釋放了能量,相應的質量也虧損了一點。這個結論已經不奇怪了,我們奇怪的是:它的質量為什么會減小?
如果我們還用牛頓的觀念思考這個問題,你就會發現怎么也想不通。你覺得一個物體的質量是組成這個物體的所有粒子質量之和,然而碳原子、氧原子組成二氧化碳分子時,原子的種類和數量都沒有變,但總質量卻減小了。整個過程除了釋放了一定的能量之外,并沒有發生其它的事情。
似乎是能量減少了一點,質量就會減少一點,就好像質量不是用來衡量組成物質的微粒,而是用來衡量能量的多少似的。
沒錯,這正是問題的關鍵:在狹義相對論里,質量確實變成了一個衡量體系能量多少的量。你靜止時有多少能量,對應的質量就是多少,它們的關系由質能方程E=mc2給出。質量不是別的什么東西,它就是能量的量度,這才是一切問題的關鍵。
以前,我們老覺得質量是物質的代名詞,覺得一卡車磚頭的質量等于每一塊磚頭的質量之和,所以每一個分子的質量就應該等于所有組成它原子的質量之和。我們是如此地相信還原論,相信所有的物質都可以還原為一個個基本粒子,相信物質的質量等于所有組成物質粒子的質量之和。
而這,正是我們理解質能方程的最大障礙。
現在我們要改變觀念,物質的質量不再是組成它基本粒子的質量之和,而是用來度量能量的。物質的能量固然包含了組成物質的基本粒子的能量,但它還包含了基本粒子之間因為相互作用而具有的能量,比如各種勢能。
比如,什么叫重力勢能?我搬起一塊石頭,石頭就增加了一定的重力勢能。因為石頭和地球之間存在引力,當石頭離開地面后,石頭和地球之間就存在這樣一種能量。石頭落地后,重力勢能減少了,度量能量的質量自然也跟著減小了,減少的能量E和質量m之間滿足E=mc2。
質子和中子組成氘核的情況也一樣,無非就是把質子和中子換成了地球和石頭,把質子和中子之間的強力換成了地球和石頭之間的引力,一個釋放了重力勢能,一個釋放了核能。
因此,只有我們認為“質量是能量的量度”,而不再是牛頓觀念里物質的代名詞,不再是衡量物質所包含基本粒子的質量之和時,我們才能邏輯一致地看待上述所有問題,才能非常自然地解釋質量虧損。
為什么質子和中子組成氘核之后,它們的質量會減小?因為獨立的質子和中子具有一定的能量,而質量是能量的量度,所以質子和中子組成的系統就具有一定的質量。質子和中子組成氘核后釋放了一定的能量E,系統的總能量減少了,度量能量的質量m自然也減小了,它們之間滿足E=mc2。
木炭燃燒變成了二氧化碳,碳原子和氧原子組合成二氧化碳分子時釋放了能量E,于是度量能量的質量m自然也減小了,它們之間依然滿足質能方程E=mc2。
我用力拉開兩個磁鐵,其實是往磁鐵組成的系統里注入了能量,磁鐵的能量增加了,度量能量的質量自然也跟著增加了。所以,分開的磁鐵會比吸在一起的磁鐵更重,你用多大能量把磁鐵拉開,它們的質量就增加了這個能量除以光速c的平方。
我們用力壓縮一個彈簧,彈簧的能量增加了,度量彈簧能量的質量自然也增加了。所以,壓縮的彈簧比松開的彈簧更重。
一個手電筒發出了一束光,因為光帶走了一部分能量,所以手電筒的能量減少了,度量手電筒能量的質量自然也減小了。于是,發光手電筒的質量會一直慢慢減小。
但是,如果我們把手電筒放在一個鐵箱子里,雖然發光手電筒的質量在不斷減小,但手電筒發出的光并沒有逃出箱子,所以手電筒和箱子的總能量并沒有減少。于是,手電筒和箱子的總質量也不會發生變化。
為什么要舉這么多例子?當然是幫你快速洗腦。
我們在牛頓的世界里浸泡了太久,已經形成了極大的思維慣性。當我們在談論物理,談論自然界的各種現象時,潛意識里就會從牛頓的角度來思考問題,所以我們會覺得相對論和量子力學很奇怪。所謂奇怪,無非就是跟固有的觀念不一樣,在這里就是跟牛頓的觀念不一樣。
17新的圖景
我們要不斷提醒自己:現在的物理圖景已經不再是牛頓那樣了,宇宙并不是一堆微粒的集合,一個物體的質量也不是組成物體實物微粒的質量之和。
如果你覺得“讓人不這樣思考”比較難,那可以接觸一下量子場論,試著從量子場的角度來看待這個世界。畢竟,讓人忘掉熟悉的舊觀念很難,但是,一旦接受了新的觀念,舊觀念自然就忘了。
量子場論首先是一種場論,它的核心思想是:宇宙并不是由什么“實物粒子”構成的,而僅僅是由場構成,一切都是場。所謂粒子,不過是這些量子化場的激發態。
然后,量子場論是量子力學和狹義相對論聯姻的產物。為什么我們要讓量子力學和狹義相對論聯姻呢?因為處理微觀粒子要用量子力學,處理高速(近光速)運動的物體要用狹義相對論。那么,如果你想處理高速的微觀粒子,就必須同時使用量子力學和狹義相對論,也就是它們聯姻后的量子場論。
也因如此,當我們用量子場論看問題時,我們其實也是在用狹義相對論看問題。而質能方程又是狹義相對論的結論,所以量子場論的圖景跟質能方程是相容的。
畢竟,如果一切都是場,沒有什么“實物粒子”,那自然就不存在什么“實物粒子被摧毀了變成能量”的說法。如果一切都是場,各種物理現象就只是場與場之間的相互作用,不存在誰被摧毀了,自然也不存在什么代表物質的“質量”轉化成了能量。
這樣,“質量轉化成能量”就完全站不住腳了。
而前面我們也說了,場是有能量的,場和場之間的相互作用自然會涉及能量的變化。能量在不斷變化,度量能量的質量自然也會不斷變化,它們的橋梁就是質能方程。
這樣,我們就可以非常自然地接受“質量是能量的量度”這個觀念了,而這,才是打開質能方程E=mc2的正確方式。
18不動的質量
不過,需要注意的是,我上面說的"質量是能量的量度",指的都是物體靜止時的能量,并不涉及物體的動能。
我們知道動能是跟參考系有關的,在一個參考系里是靜止的物體(動能為0),在另一個參考系里可能就是運動的(動能不為0),動能并不一樣。
因此,如果把動能考慮進去,速度的增加就會導致動能的增加,能量增加了對應的質量也會增加。這樣,物體的質量就會隨著速度的增加而增加,也就是所謂的動質量。
但是,我非常不希望引入動質量。物理學要把握變化世界里不變的東西,質量原本是跟物體的運動狀態無關的,你現在讓它隨著速度的變化而變化,何必呢?動質量又不是非用不可,我的文章從頭到尾都沒有動質量,不一樣可以講質能方程么?
我知道,有些地方是從動質量開始講質能方程的。他們先定義動質量,再把狹義相對論的新動量定義為動質量和速度的乘積,然后去算新動能。
這樣讀者就會很困惑,你憑什么把新動量定義為動質量和速度的乘積?難道狹義相對論就是用動質量替換掉原來的質量,剩下的照搬?然后各種腦洞大開,胡思亂想。
在這篇文章里,我只是堅持狹義相對論的基本原理,要求動量守恒定律在洛倫茲變換下保持數學形式不變,然后自然就得到了新動量:
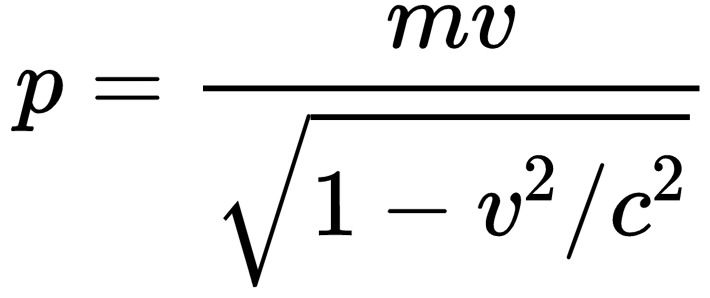
這樣邏輯上就非常自然。在這個新動量里,質量m依然是不隨物體的運動狀態而改變的質量,動量是一個速度的函數,而不是動質量和速度的乘積。
另外,我們再看一看狹義相對論的新動能:
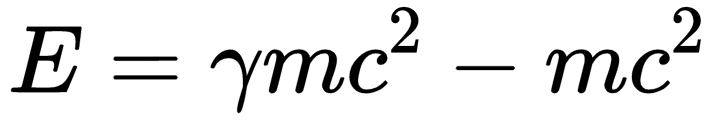
愛因斯坦認為mc2是物體靜止時的能量,E是物體的動能,所以γmc2就是物體的總能量(動能+靜能):γmc2=E+mc2。
現在我們說“質量是能量的量度”,如果這個能量指的是物體靜止時的能量mc2,那質量就是(靜)質量;如果我們把動能E也加進來,認為能量是總能量γmc2, 那得到的就是動質量。
也就是說,動質量和總能量在某種程度上是在描述相同的東西。然而,總能量是一直都存在的,并且是個非常重要的守恒量。如果已經存在一個守恒的總能量,為什么還要引入會導致混亂的動質量呢?
因此,我在文章里提到的質量通通都是(靜)質量,完全不用動質量這種東西,也省得大家胡思亂想,最后把自己帶溝里去了。
當然,雖然學界的主流是舍棄動質量,但也有少數學者認為動質量依然有存在的必要,這個我就不多說了,感興趣的自己去查。
19結語
寫到這里,文章差不多就可以收尾了。
通觀全文,大家會發現質能方程的推導還是很簡單的,只要遵守狹義相對論的基本原理,E=mc2就會自動地從動能表達式里冒出來。
真正困難的,還是理解質能方程背后世界觀和物質觀的轉變,理解從牛頓到狹義相對論的轉變,理解從“質量轉化成能量”到“質量是能量的量度”的轉變。
雖然相對論和量子力學革命已經過去了百年,但牛頓的觀念還是深深地烙在許多人的心里。畢竟,我們在中學都要學習牛頓力學,只有少數人會系統地學習相對論和量子力學,而這方面的科普又比較少。
所以,習慣于用牛頓的觀念去理解質能方程并不奇怪。
但話又說回來,畢竟如今已經是21世紀了,相對論和量子力學已經極大地改變了牛頓的世界觀和物質觀。如果你對后牛頓時代的物理學不感興趣也就罷了,如果感興趣(比如質能方程),就一定要注意牛頓觀念的局限性。
我們不能總是從牛頓的角度來考慮這些后牛頓時代的物理學,否則,我們不僅無法掌握這些內容,還會誤入歧途。
如果你能很好地理解質能方程,就能很好地理解狹義相對論,也能很好地理解從牛頓到現代物理的轉變,這是一塊非常好的試金石。
所以,現在你明白質能方程E=mc2了么?
再復雜的科學,也有簡單的邏輯。我是一邊學習一邊寫科普的長尾君,只有給你講明白了,我才算學懂了。如果你想跟我一起學習,或者學科普,歡迎長按加入下方的知識星球(或閱讀原文),我拉你進微信群。文章呈現的只是最終結果,更多精華盡在社群的日常學習、討論中,歡迎跟我一起學習、成長~
編輯:jq
-
能量
+關注
關注
0文章
105瀏覽量
16539 -
電磁場
+關注
關注
0文章
794瀏覽量
47361 -
粒子
+關注
關注
0文章
44瀏覽量
12681 -
方程
+關注
關注
0文章
33瀏覽量
16947 -
原子
+關注
關注
0文章
89瀏覽量
20329
原文標題:你也能懂的質能方程E=mc2
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
燧原科技入選先進計算賦能新質生產力典型應用案例
無極電容器有電解質嗎,無極電容器電解質怎么測
TAS6424E-Q1 4.2K負載配置normal模式也能播放,為什么?
請問OPA549可以吸收電流嗎?能吸收多大電流?
機械革命入選《2024全國企業新質生產力賦能典型案例》

匠心智造 提質增效 | 新質生產力賦能高質量發展論壇暨木幾新產品發布會圓滿成功!

AN75664是否可以將DMA_WM_THn用作DR_DATA狀態下的轉換方程?
探尋杭州新質生產力,300米外的信號也能閃連





 你也可以懂的質能方程E=mc2
你也可以懂的質能方程E=mc2













評論