阻抗及輸入阻抗和輸出阻抗解析
阻抗是電阻和電抗的統稱,電阻和電抗最大的差異在于電阻限流(歐姆定律)的同時會消耗電能。而電抗只限流,不消耗電能(不做功)。電阻在直流電和交流電下都有限流作用,而電抗只在交流電環境中有限流作用。
輸入阻抗(input impedance)是指一個電路輸入端的等效阻抗。在輸入端上加上一個電壓源U,測量輸入端的電流I,則輸入阻抗Rin就是U/I。你可以把輸入端想象成一個電阻的兩端,這個電阻的阻值,就是輸入阻抗。
在同樣的輸入電壓的情況下,如果輸入阻抗很低,就需要流過較大電流,這就要考驗前級的電流輸出能力了;而如果輸入阻抗很高,那么只需要很小的電流,這就為前級的電流輸出能力減少了很大負擔。所以電路設計中盡量提高輸入阻抗。
輸入阻抗跟一個普通的電抗元件沒什么兩樣,它反映了對電流阻礙作用的大小。
對于電壓驅動的電路,輸入阻抗越大,則對電壓源的負載就越輕,因而就越容易驅動,也不會對信號源有影響;而對于電流驅動型的電路,輸入阻抗越小,則對電流源的負載就越輕。
因此,我們可以這樣認為:如果是用電壓源來驅動的,則輸入阻抗越大越好;如果是用電流源來驅動的,則阻抗越小越好(注:只適合于低頻電路,在高頻電路中,還要考慮阻抗匹配問題。)另外如果要獲取最大輸出功率時,也要考慮阻抗匹配問題。
輸出阻抗
輸出阻抗(output impedance) 含獨立電源網絡輸出端口的等效電壓源(戴維南等效電路)或等效電流源(諾頓等效電路)的內阻抗。其值等于獨立電源置零時,從輸出端口視入的輸入阻抗。
無論信號源或放大器還有電源,都有輸出阻抗的問題。輸出阻抗就是一個信號源的內阻。本來,對于一個理想的電壓源(包括電源),內阻應該為0,或理想電流源的阻抗應當為無窮大。輸出阻抗在電路設計最特別需要注意。
現實中的電壓源,則做不到這一點,常用一個理想電壓源串聯一個電阻r的方式來等效一個實際的電壓源。這個跟理想電壓源串聯的電阻r就是信號源/放大器輸出/電源的內阻了。
當這個電壓源給負載供電時,就會有電流I從這個負載上流過,并在這個電阻上產生I×r的電壓降。這將導致電源輸出電壓的下降,從而限制了最大輸出功率。
同樣的,一個理想的電流源,輸出阻抗應該是無窮大,但實際的電路是不可能的。
輸出阻抗,是指電路負載從電路輸出端口反著看進電路時電路所等效的阻抗,其實主要是針對能量源或者輸出電路來說的,是能量源在輸出端測到的阻抗,俗稱內阻。
阻抗思維分析開關電路
如下圖,V1持續向R1在輸送電流,圖中電流回路如綠色箭頭所示。如果想控制電流流向R1,我們有哪些辦法?
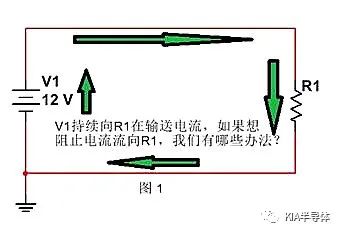
最常見的方法是,斷開V1和R1之間的連接,切斷電流回路。如下圖所示。
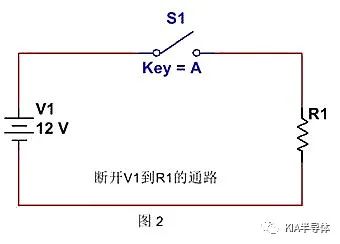
或者我們可以把R1旁路,如下圖所示。將R1前面加一條導線,把電流引向阻抗低的通路上,R1上將獲得忽略不計的電流。
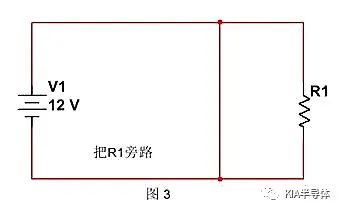
上述兩種方法,都很直截了當,要么將V1到R1的通路徹底斷開,要么短路R1,解決的很徹底。但是在工程的世界里,我們無法做的這么干脆利落,往往講究個“差不多”就行。所以,“短路模型”我們只能做到“低阻抗”,“開路模型”我們只能做到“高阻抗”,能量被大幅度“衰減”,我們就認為達標了。
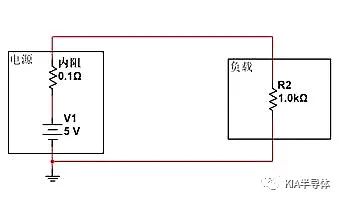
如下圖所示,下圖為實際的電源-負載模型。我們看如何通過調整阻抗來達到開關效果。實際電路中的電源都有輸出能力限制和內阻,輸出電流越大,輸出電壓也會越低。
如下內阻為0.1Ω,負載為1KΩ的電路。在當前情況下,負載兩端獲得的電壓為內阻和R2分壓而成。我們可以計算出V=5V*(1K/(1K+0.1))=4.9999V,I=5V/1000.1Ω=4.9mA。
如果我們用“開路模型”的方法來斷開電路,該怎么調整阻抗呢?就是在電源和負載之間串接遠大于1K的電阻,進行串聯分壓,使得R2上獲得的電壓更小。如下圖,若串聯的1M電阻與負載分壓。我們可以計算出負載兩端最終分配的電壓:
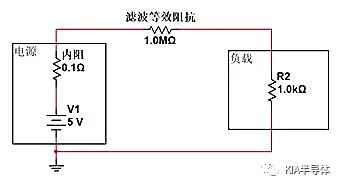
V=5V*(1K/(0.1+1000K+1K))=0.00499V,I=5V/1001000.1Ω=0.0049mA。幅值削弱了接近1000倍,在工程思維上,R2近似于被“斷開”了。
如果我們用“短路模型”的方法來斷開R2,該怎么調整呢?就是在負載前端并聯遠小于0.1Ω的電阻,與內阻進行串聯分壓,使得R2上獲得的電壓更小。
如下圖,若濾波措施等效為并聯的0.005Ω電阻與內阻分壓。我們可以計算出負載R2兩端最終分配的電壓:
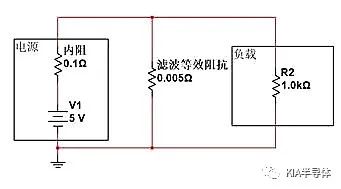
V=5V*(0.0049/(0.1+0.0049)=0.233V。幅值削弱了接近20倍,在工程思維上,R2同樣近似于被“斷開”了。
如上就是半導體開關電路的理論模型,以反相器電路為例:
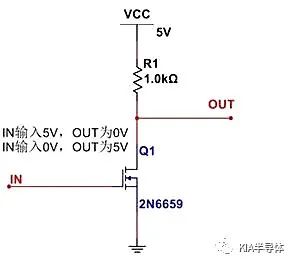
當IN端加高電平時,我們會說MOS管Q1導通。此時的導通狀態相當于Q1變成了一個阻抗為幾十毫歐的電阻,然后與R1電阻進行分壓。假如上拉電阻R1太小,也為幾十毫歐,那即使IN為高,Q1導通,OUT端也無法輸出低電平。
當IN端加低電平時,我們會說MOS管Q1截止。此時的截止狀態相當于Q1變成了一個阻抗為幾兆歐的電阻,與R1電阻進行分壓。假如上拉電阻R1太大,也為幾兆歐,那即使IN為低,Q1截止,OUT端也無法輸出高電平。
所以深入理解開關電路時,要以阻抗的思維去分析。
阻抗思維分析濾波電路
在此,用阻抗思維分析下濾波電路。
實際工程應用中,一個電源輸出中往往包含不同頻率的交流成分,有我們想要的,也有我們不想要的。而電感和電容的阻抗會隨著頻率變化。正是因為這個特點,電感和電容成了濾波電路中當仁不讓的主角。
還是如下電路,假設該電源包含的頻譜分量為0-1GHz。

假如我們要為負載R2濾除掉高頻的交流分量,我們會發現串聯電感或者并聯電容的方式都可以滿足要求。
如下圖,若在電源和負載上串聯1顆16uH的電感,100MHz交流分量會衰減多少?根據電感的阻抗公式:ZL=2πfL=2*3.14*100MHz*16uH,可以求得ZL=10K。
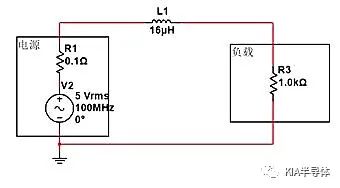
根據串聯分壓公式,R3兩端電壓/輸入=R3/(R3+ZL)=1K/11K=0.0909。所以電源幅值為5V時,R3兩端幅值僅為5V*0.0909=0.45V。
100MHz時,用示波器分別量測濾波前和濾波后的波形對比如下,可見100MHz波形效果,實際量測為0.449V,和分析結果一致。
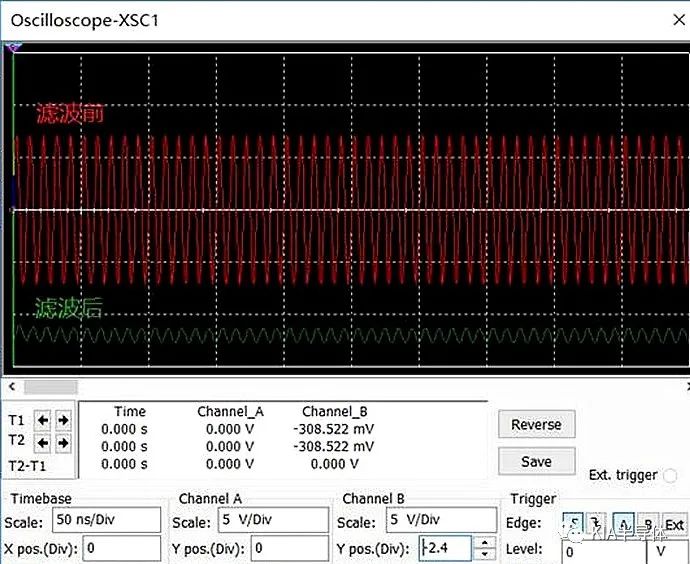
阻抗思維分析低通濾波器
通過在電源和負載中間串聯電感,在負載前端并聯電容,就組成了低通濾波器電路。
如下,假如C1=1uF,L1=22uH,求該濾波電路對100MHZ交流分量的衰減程度是多少?
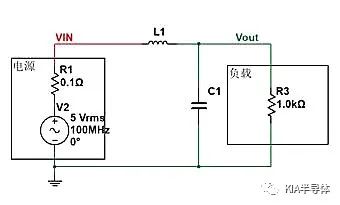
此時,該電路是電容(C1)的阻抗Zc和R3并聯后,再和電感(L1)阻抗ZL進行分壓。所以我們可以列出阻抗方程(就是簡單的串聯分壓公式)。
衰減幅度=Vout/Vin=(Zc//R3)/(ZL+(Zc//R3)),
其中Zc=1/2πfC,ZL=2πfL。已知R3=1KΩ,可得
Zc=0.0015Ω,Zc//R=0.00149Ω。
ZL=13816Ω,可求得衰減幅度=0.00149/(13816.00149)=0.000000178。
可見100MHz的交流分量幾乎無法通過22uH,1uF的低通濾波電路。同時我們也看到,負載R3也會影響濾波器濾波效果。所以我們有時候會發現同樣的濾波器電路,在這個電路上效果好,別的電路上效果差。
編輯:jq
-
串聯
+關注
關注
6文章
424瀏覽量
37653 -
電路
+關注
關注
172文章
5959瀏覽量
172713 -
電容
+關注
關注
100文章
6090瀏覽量
150774 -
濾波器
+關注
關注
161文章
7858瀏覽量
178668 -
示波器
+關注
關注
113文章
6279瀏覽量
185624
原文標題:阻抗及輸入阻抗和輸出阻抗解析
文章出處:【微信號:KIA半導體,微信公眾號:KIA半導體】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
請問SN74CBT3251的輸出阻抗是多少?ADC10321的輸入阻抗是多少?
ADC的輸入阻抗能達到多大,輸入阻抗很大是否更容易受干擾?
ADS1258的輸入阻抗是多少?
阻抗對信號傳輸的影響 阻抗測量儀器的選擇
阻抗對音頻設備的影響 靜態阻抗和動態阻抗的區別
安泰: 功率放大器的輸出阻抗是什么意思





 全面剖析阻抗及輸入阻抗和輸出阻抗
全面剖析阻抗及輸入阻抗和輸出阻抗












評論