可是,你能夠如數家珍地說出所有常用的分類算法,以及他們的特征、優缺點嗎?比如說,你可以快速地回答下面的問題么:
KNN算法的優缺點是什么?
Naive Bayes算法的基本假設是什么?
entropy loss是如何定義的?
最后,分類算法調參常用的圖像又有哪些?
答不上來?別怕!一起來通過這篇文章回顧一下機器學習分類算法吧(本文適合已有機器學習分類算法基礎的同學)。
機器學習是一種能從數據中學習的計算機編程科學以及藝術,就像下面這句話說得一樣。
機器學習是使計算機無需顯式編程就能學習的研究領域。 ——阿瑟·塞繆爾,1959年
不過還有一個更好的定義:
“如果一個程序在使用既有的經驗(E)執行某類任務(T)的過程中被認為是“具備學習能力的”,那么它一定需要展現出:利用現有的經驗(E),不斷改善其完成既定任務(T)的性能(P)的特性。” ——Tom Mitchell, 1997
例如,你的垃圾郵件過濾器是一個機器學習程序,通過學習用戶標記好的垃圾郵件和常規非垃圾郵件示例,它可以學會標記垃圾郵件。系統用于學習的示例稱為訓練集。在此案例中,任務(T)是標記新郵件是否為垃圾郵件,經驗(E)是訓練數據,性能度量(P) 需要定義。例如,你可以定義正確分類的電子郵件的比例為P。這種特殊的性能度量稱為準確度,這是一種有監督的學習方法,常被用于分類任務。
機器學習入門指南:
https://builtin.com/data-science/introduction-to-machine-learning
監督學習
在監督學習中,算法從有標記數據中學習。在理解數據之后,該算法通過將模式與未標記的新數據關聯來確定應該給新數據賦哪種標簽。
監督學習可以分為兩類:分類和回歸。
分類問題預測數據所屬的類別;
分類的例子包括垃圾郵件檢測、客戶流失預測、情感分析、犬種檢測等。
回歸問題根據先前觀察到的數據預測數值;
回歸的例子包括房價預測、股價預測、身高-體重預測等。
機器學習新手的十大算法之旅:
https://builtin.com/data-science/tour-top-10-algorithms-machine-learning-newbies
分類問題
分類是一種基于一個或多個自變量確定因變量所屬類別的技術。

分類用于預測離散響應
邏輯回歸
邏輯回歸類似于線性回歸,適用于因變量不是一個數值字的情況 (例如,一個“是/否”的響應)。它雖然被稱為回歸,但卻是基于根據回歸的分類,將因變量分為兩類。
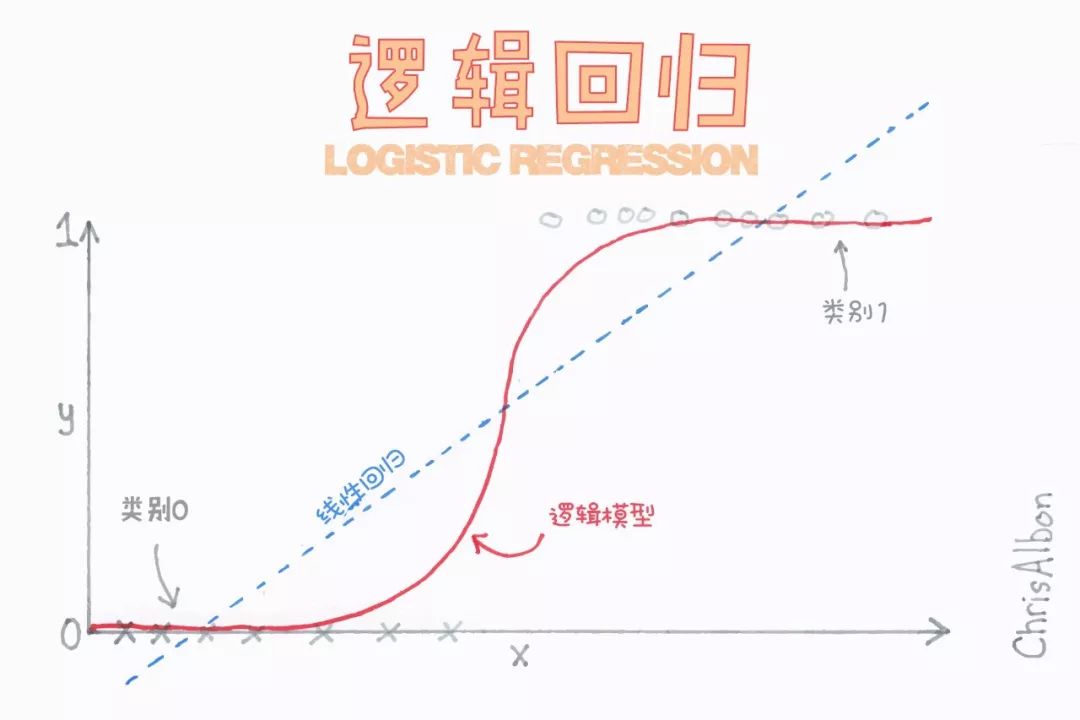
如上所述,邏輯回歸用于預測二分類的輸出。例如,如果信用卡公司構建一個模型來決定是否通過向客戶的發行信用卡申請,它將預測客戶的信用卡是否會“違約”。 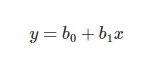 首先對變量之間的關系進行線性回歸以構建模型,分類的閾值假設為0.5。
首先對變量之間的關系進行線性回歸以構建模型,分類的閾值假設為0.5。 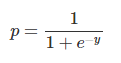
然后將Logistic函數應用于回歸分析,得到兩類的概率。
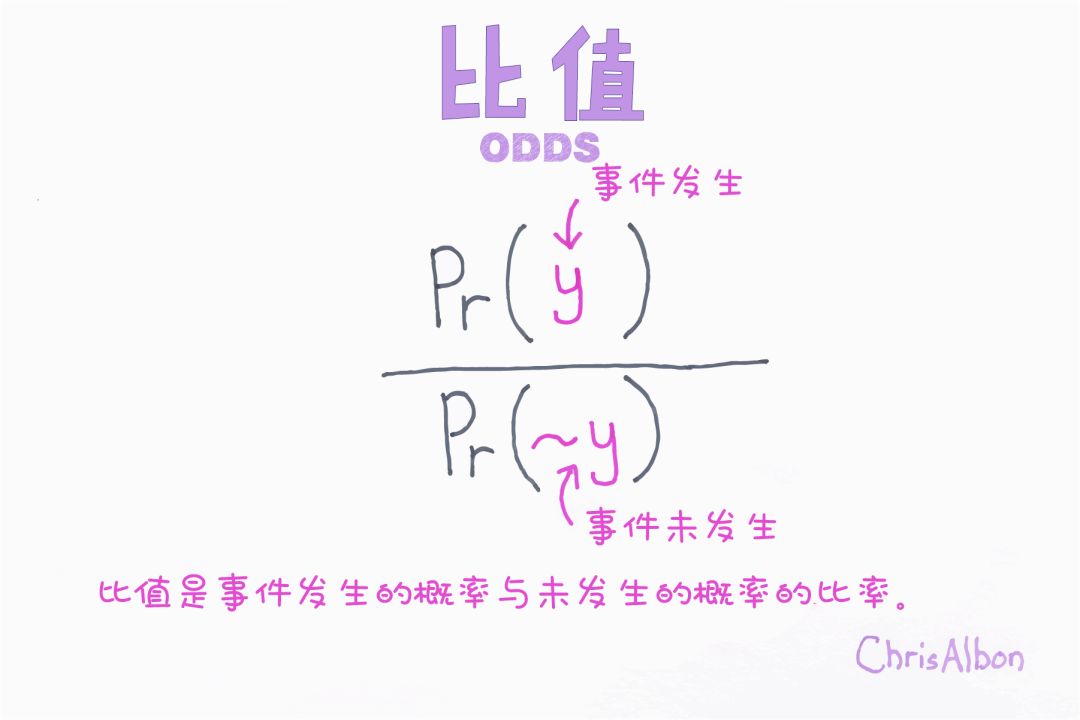
該函數給出了事件發生和不發生概率的對數。最后,根據這兩類中較高的概率對變量進行分類。
K-近鄰算法(K-NN)
K-NN算法是一種最簡單的分類算法,通過識別被分成若干類的數據點,以預測新樣本點的分類。K-NN是一種非參數的算法,是“懶惰學習”的著名代表,它根據相似性(如,距離函數)對新數據進行分類。
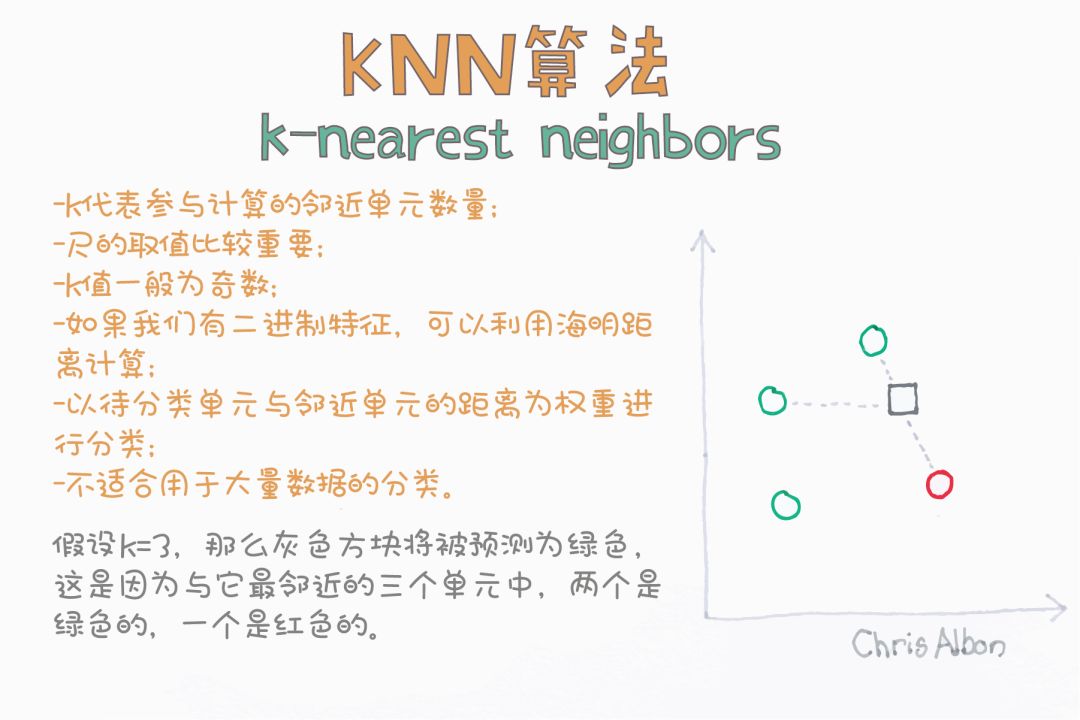


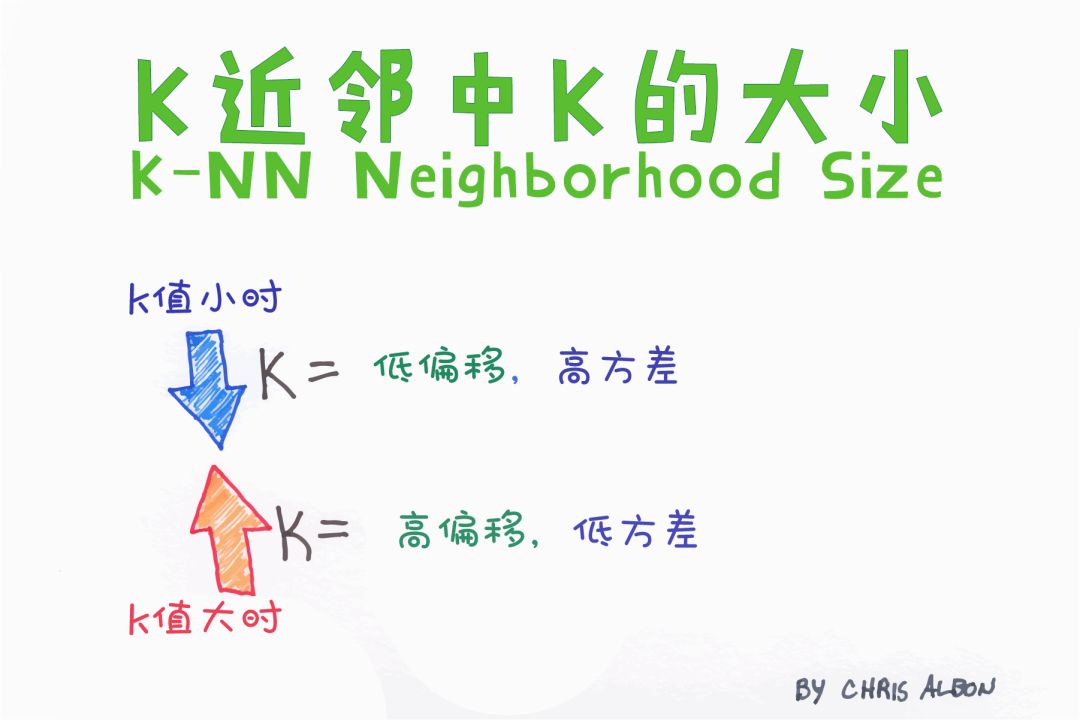
K-NN能很好地處理少量輸入變量(p)的情況,但當輸入量非常大時就會出現問題。
支持向量機(SVM)
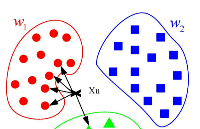
支持向量機既可用于回歸也可用于分類。它基于定義決策邊界的決策平面。決策平面(超平面)可將一組屬于不同類的對象分離開。
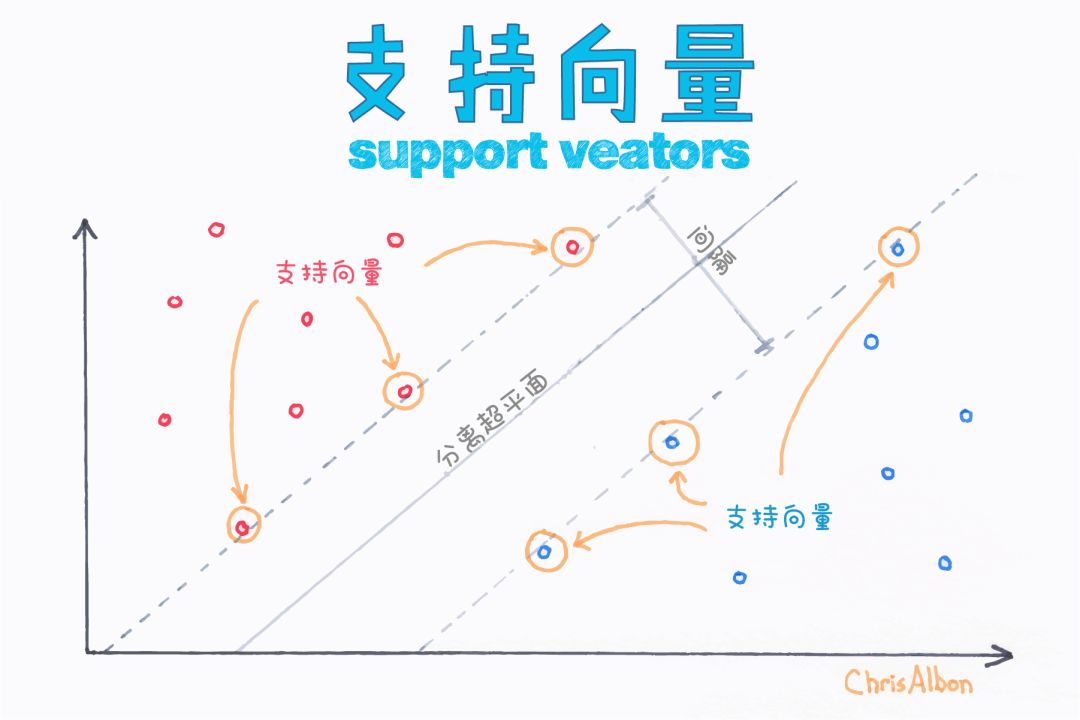
在支持向量的幫助下,SVM通過尋找超平面進行分類,并使兩個類之間的邊界距離最大化。
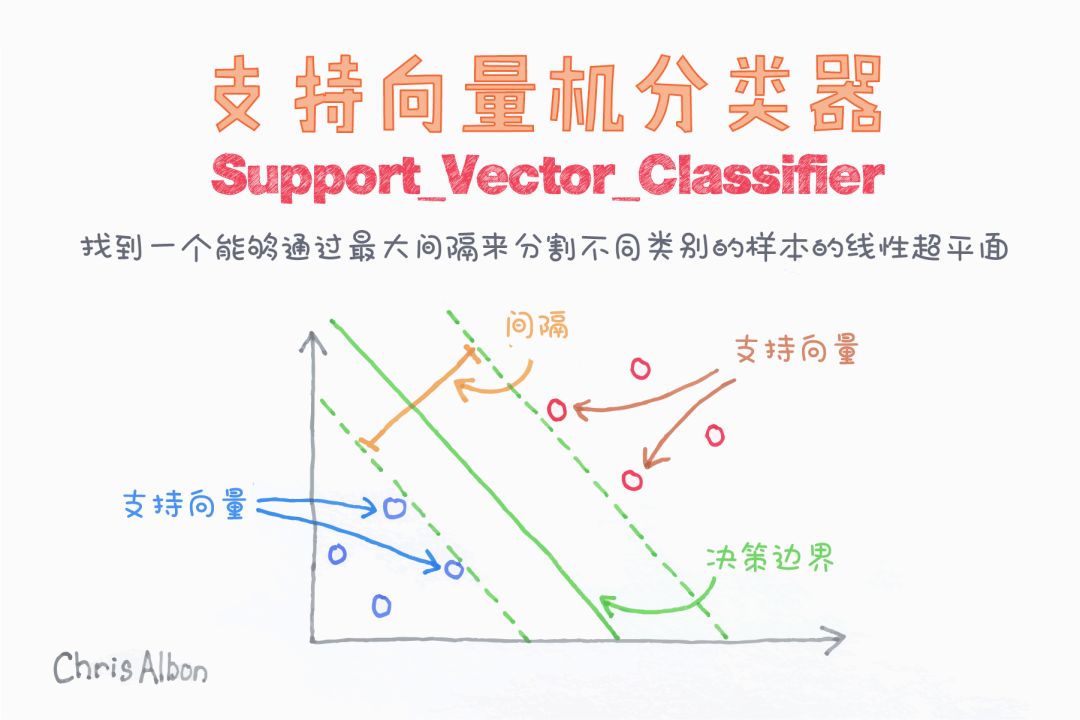
SVM中超平面的學習是通過將問題轉化為使用一些某種線性代數轉換問題來完成的。(上圖的例子是一個線性核,它在每個變量之間具有線性可分性)。
對于高維數據,使用可使用其他核函數,但高維數據不容易進行分類。具體方法將在下一節中闡述。
核支持向量機
核支持向量機將核函數引入到SVM算法中,并將其轉換為所需的形式,將數據映射到可分的高維空間。
核函數的類型包括:
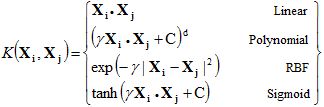
前文討論的就是線性SVM。
多項式核中需要指定多項式的次數。它允許在輸入空間中使用曲線進行分割。
徑向基核(radial basis function, RBF)可用于非線性可分變量。使用平方歐幾里德距離,參數的典型值會導致過度擬合。sklearn中默認使用RBF。
類似于與邏輯回歸類似,sigmoid核用于二分類問題。
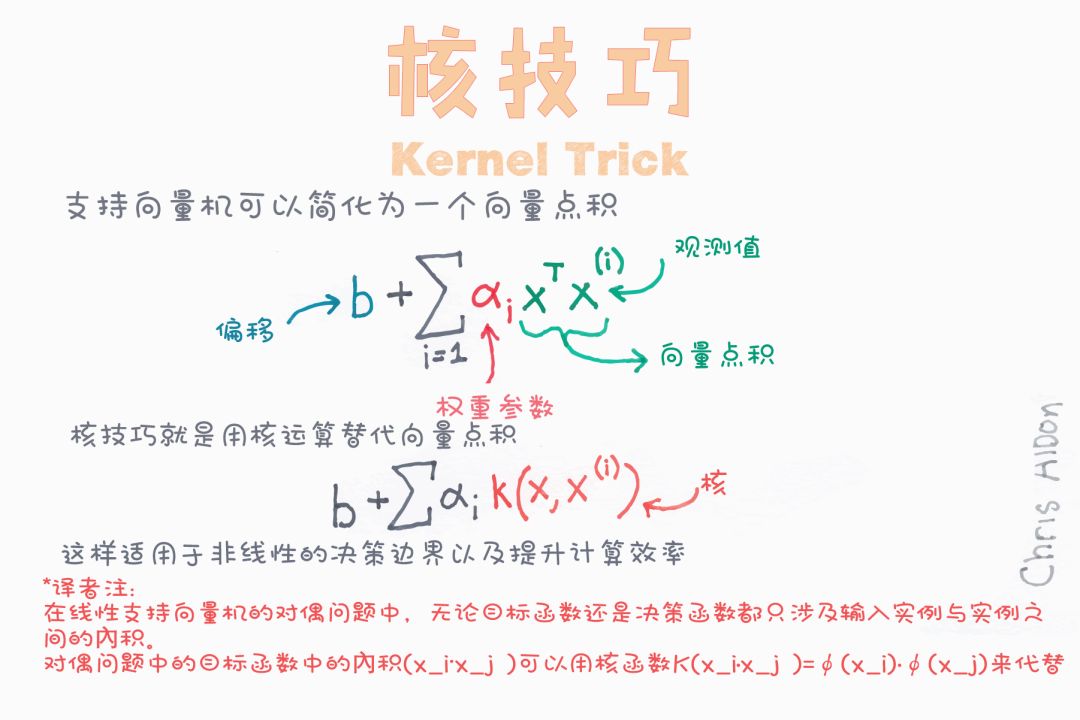
徑向基核(RBF:Radial Basis Function )
RBF核支持向量機的決策區域實際上也是一個線性決策區域。RBF核支持向量機的實際作用是構造特征的非線性組合,將樣本映射到高維特征空間,再利用線性決策邊界分離類。
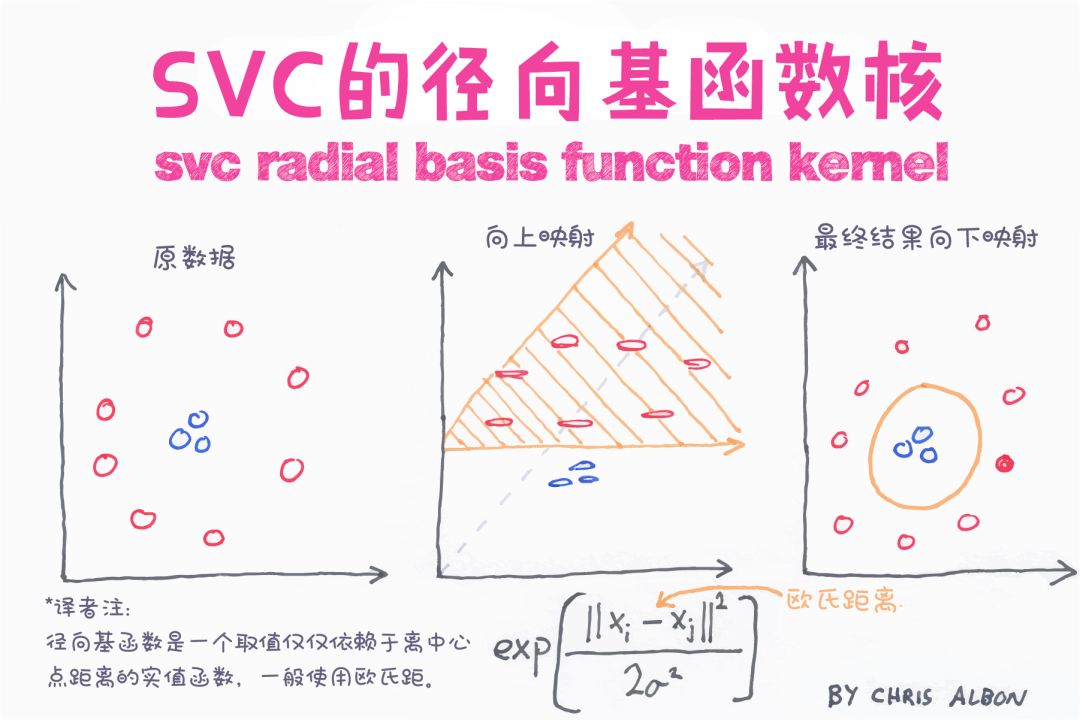
因此,可以得出經驗是:對線性問題使用線性支持向量機,對非線性問題使用非線性核函數,如RBF核函數。
樸素貝葉斯
樸素貝葉斯分類器建立在貝葉斯定理的基礎上,基于特征之間互相獨立的假設(假定類中存在一個與任何其他特征無關的特征)。即使這些特征相互依賴,或者依賴于其他特征的存在,樸素貝葉斯算法都認為這些特征都是獨立的。這樣的假設過于理想,樸素貝葉斯因此而得名。

在樸素貝葉斯的基礎上,高斯樸素貝葉斯根據二項(正態)分布對數據進行分類。
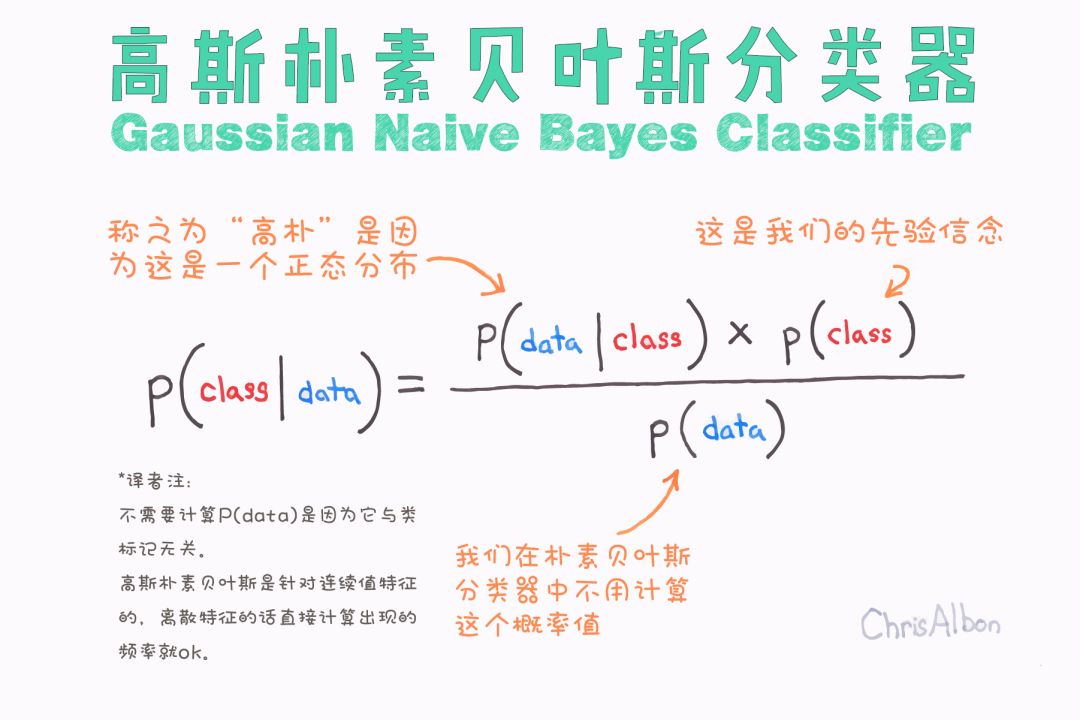
P(class|data)表示給定特征(屬性)后數據屬于某類(目標)的后驗概率。給定數據,其屬于各類的概率大小就是我們要計算的值。 P(class)表示某類的先驗概率。 P(data|class)表示似然,是指定類別時特征出現的概率。 P(data)表示特征或邊際似然的先驗概率。
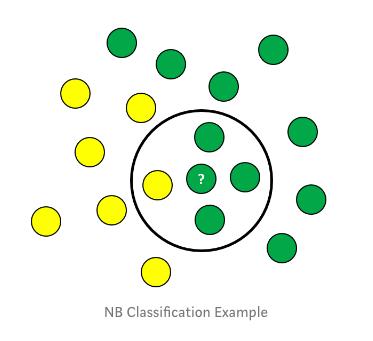
步驟
1、計算先驗概率P(class)= 類中數據點的數量/觀測值的總數量 P(yellow)= 10/17 P(green)= 7/17
2、計算邊際似然P(data)= 與觀測值相似的數據點的數量/觀測值的總數量 P(?)= 4/17 該值用于檢查各個概率。
3、計算似然P(data/class)= 類中與觀測值相似的數量/類中點的總數量 P(?/yellow)= 1/7 P(?/green)= 3/10
4、計算各類的后驗概率

5、分類

某一點歸于后驗概率高的類別,因為從上可知其屬于綠色類的概率是75%根據其75%的概率這個點屬于綠色類。
多項式、伯努利樸素貝葉斯是計算概率的其他模型。樸素貝葉斯模型易于構建,不需要復雜的參數迭代估計,這使得它對非常大的數據集特別有用。
決策樹分類
決策樹以樹狀結構構建分類或回歸模型。它通過將數據集不斷拆分為更小的子集來使決策樹不斷生長。最終長成具有決策節點(包括根節點和內部節點)和葉節點的樹。最初決策樹算法它采用采用Iterative Dichotomiser 3(ID3)算法來確定分裂節點的順序。
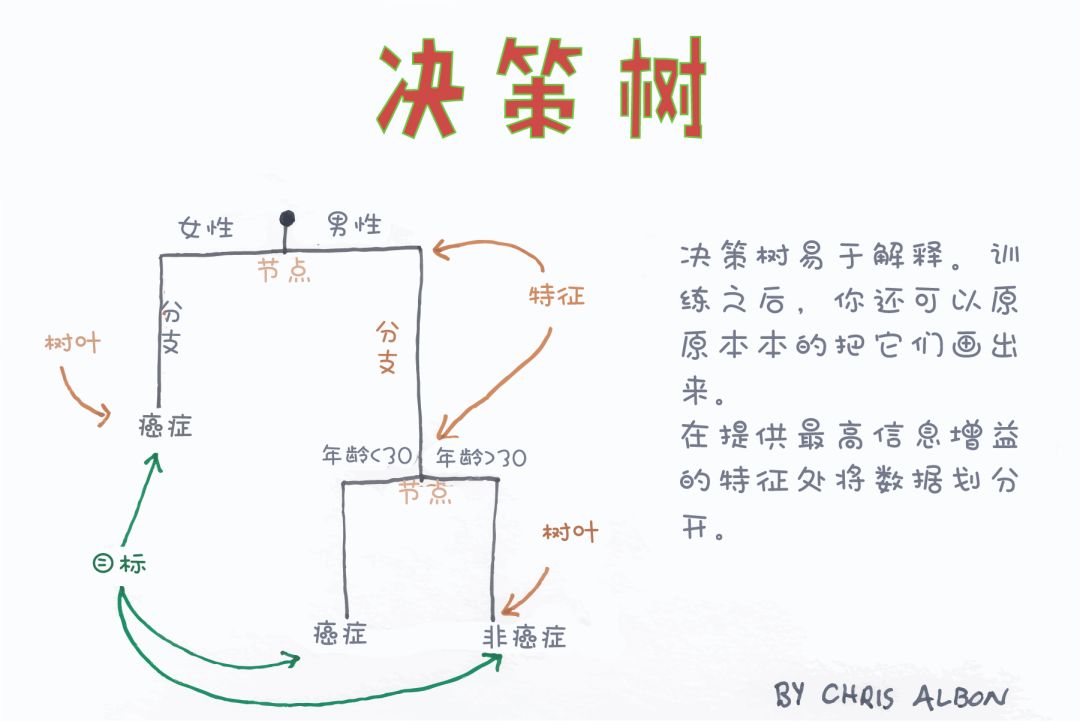
信息熵和信息增益用于被用來構建決策樹。
信息熵
信息熵是衡量元素無序狀態程度的一個指標,即衡量信息的不純度。
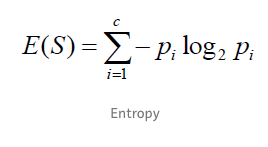
信息熵是衡量元素的無序狀態的程度的一個指標,或者說,衡量信息的不純度。
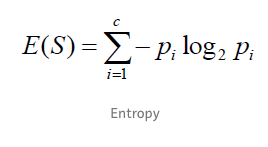
直觀上說地理解,信息熵表示一個事件的確定性程度。信息熵度量樣本的同一性,如果樣本全部屬于同一類,則信息熵為0;如果樣本等分成不同的類別,則信息熵為1。
信息增益
信息增益測量獨立屬性間信息熵的變化。它試圖估計每個屬性本身包含的信息,構造決策樹就是要找到具有最高信息增益的屬性(即純度最高的分支)。
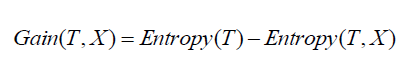
信息增益測量獨立屬性間的信息熵的變化。它試圖估計每個屬性本身包含的信息,構造決策樹就是要找到具有最高信息增益的屬性(即純度最高的分支)。
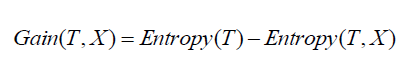
其中Gain((T,X))是特征X的信息增益。Entropy(T)是整個集合的信息熵,第二項Entropy(T,X)是特征X的信息熵。
采用信息熵進行節點選擇時,通過對該節點各個屬性信息增益進行排序,選擇具有最高信息增益的屬性作為劃分節點,過濾掉其他屬性。
決策樹模型存在的一個問題是容易過擬合。因為在其決策樹構建過程中試圖通過生成長一棵完整的樹來擬合訓練集,因此卻降低了測試集的準確性。
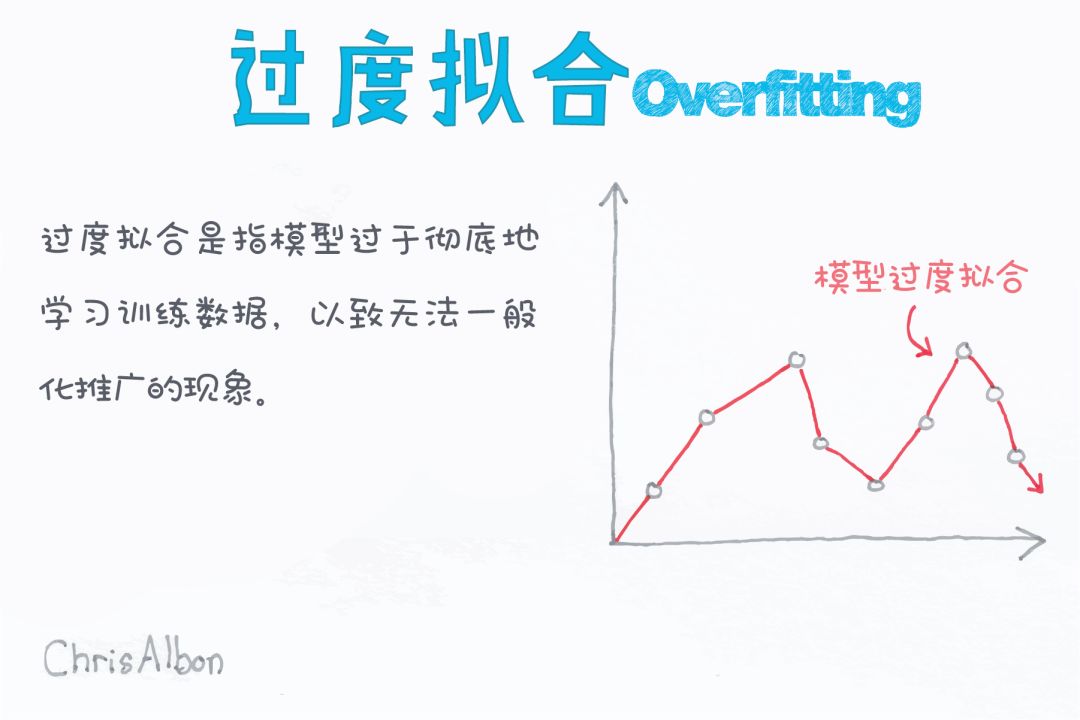
通過剪枝技術可以減少小決策樹的過擬合問題。
分類的集成算法
集成算法是一個模型組。從技術上說,集成算法是單獨訓練幾個有監督模型,并將訓練好的模型以不同的方式進行融合,從而達到最終的得預測結果。集成后的模型比其中任何一個單獨的模型都有更高的預測能力。

隨機森林分類器
隨機森林分類器是一種基于裝袋(bagging)的集成算法,即自舉助聚合法(bootstrap aggregation)。集成算法結合了多個相同或不同類型的算法來對對象進行分類(例如,SVM的集成,基于樸素貝葉斯的集成或基于決策樹的集成)。
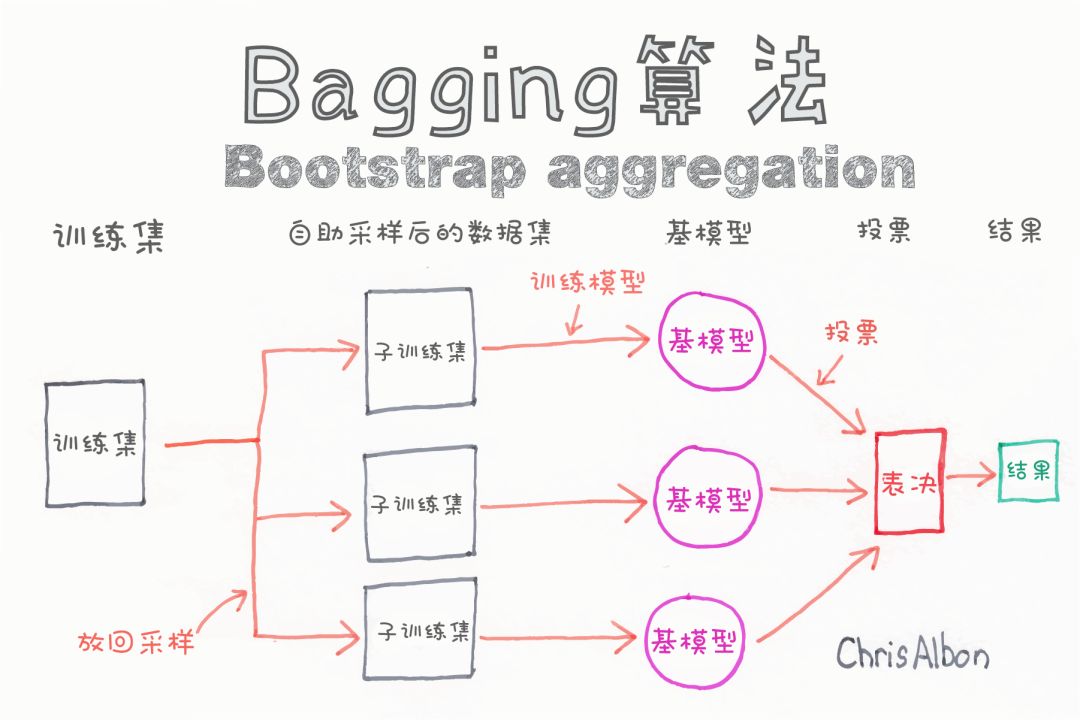
集成的基本思想是算法的組合提升了最終的結果。
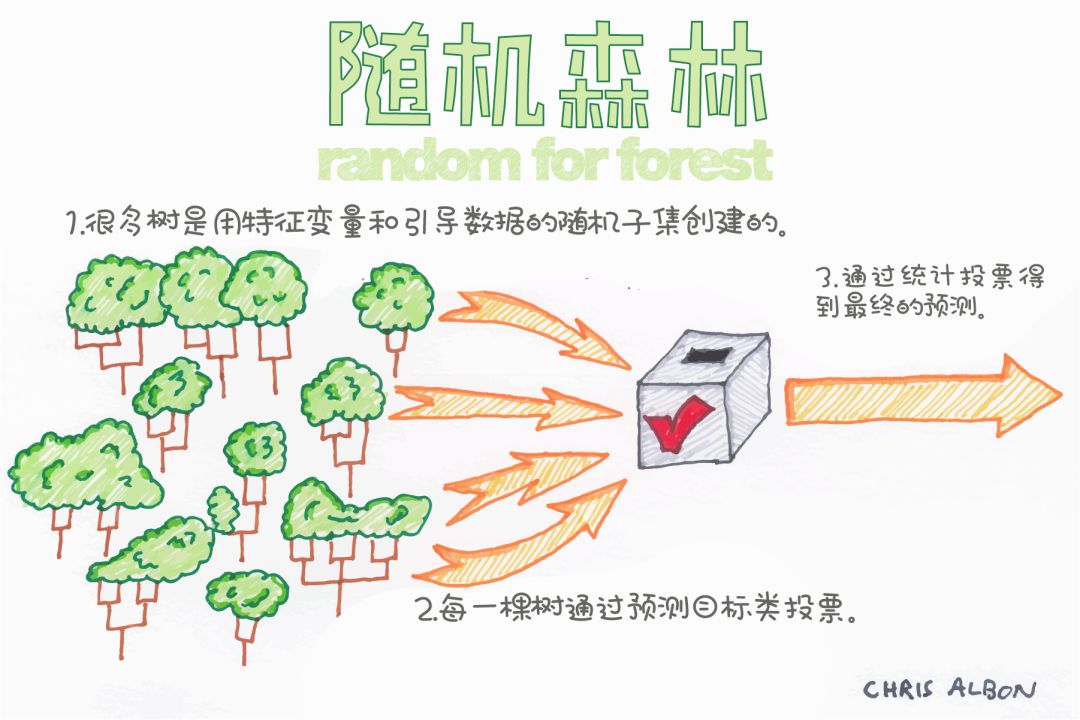
深度太大的決策樹容易受過擬合的影響。但是隨機森林通過在隨機子集上構建決策樹防止過擬合,主要原因是它會對所有樹的結果進行投票的結果是所有樹的分類結果的投票,從而消除了單棵樹的偏差。
隨機森林在決策樹生增長的同時為模型增加了額外的隨機性。它在分割節點時,不是搜索全部樣本最重要的特征,而是在隨機特征子集中搜索最佳特征。這種方式使得決策樹具有多樣性,從而能夠得到更好的模型。
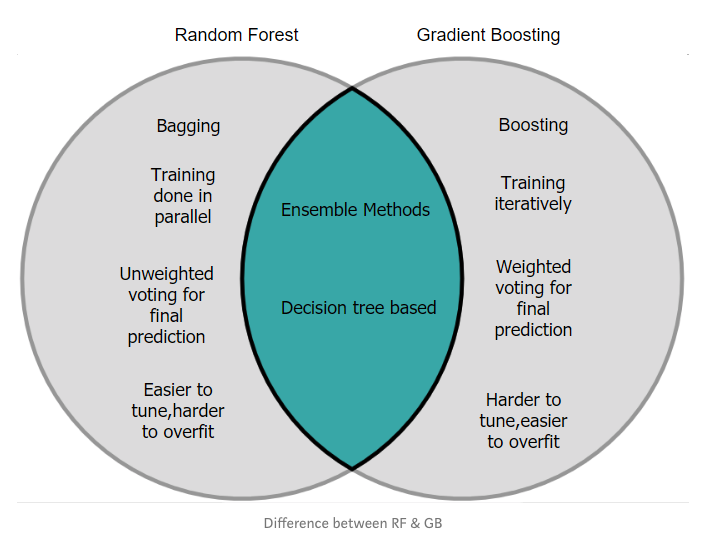
梯度提升分類器
梯度提升分類器是一種提升集成算法。提升(boosting)算法是為了減少偏差而對弱分類器的而進行的一種集成方法。與裝袋(bagging)方法構建預測結果池不同,提升算法是一種分類器的串行方法,它把每個輸出作為下一個分類器的輸入。通常,在裝袋算法中,每棵樹在原始數據集的子集上并行訓練,并用所有樹預測結果的均值作為模型最終的預測結果;梯度提升模型,采用串行方式而非并行模式獲得預測結果。每棵決策樹預測前一棵決策樹的誤差,因而使誤差獲得提升。

梯度提升樹的工作流程
使用淺層決策樹初始化預測結果。
計算殘差值(實際預測值)。
構建另一棵淺層決策樹,將上一棵樹的殘差作為輸入進行預測。
用新預測值和學習率的乘積作為最新預測結果,更新原有預測結果。
重復步驟2-4,進行一定次數的迭代(迭代的次數即為構建的決策樹的個數)。
如果想了解更多關于梯度提升分類器的知識,可參考:
https://medium.com/mlreview/gradient-boosting-from-scratch-1e317ae4587d%20/t%20_blank
分類器的性能
混淆矩陣
混淆矩陣是一張表,這張表通過對比已知分類結果的測試數據的預測值和真實值表來描述衡量分類器的性能。在二分類的情況下,混淆矩陣是展示預測值和真實值四種不同結果組合的表。

多分類問題的混淆矩陣可以幫助你確認錯誤模式。
對于二元分類器:
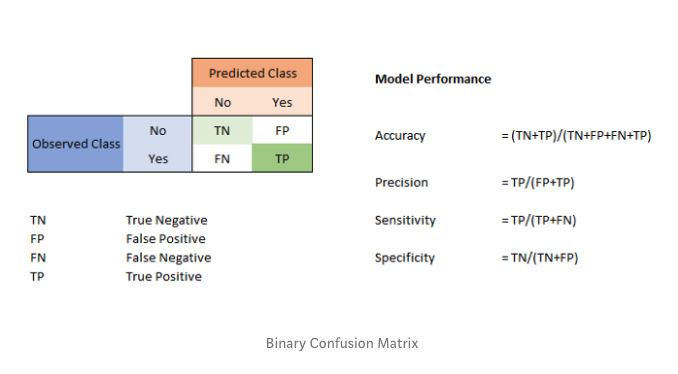
假正例&假負例
假正例和假負例用來衡量模型預測的分類效果。假正例是指模型錯誤地將負例預測為正例。假負例是指模型錯誤地將正例預測為負例。主對角線的值越大(主對角線為真正例和真負例),模型就越好;副對角線給出模型的最差預測結果。
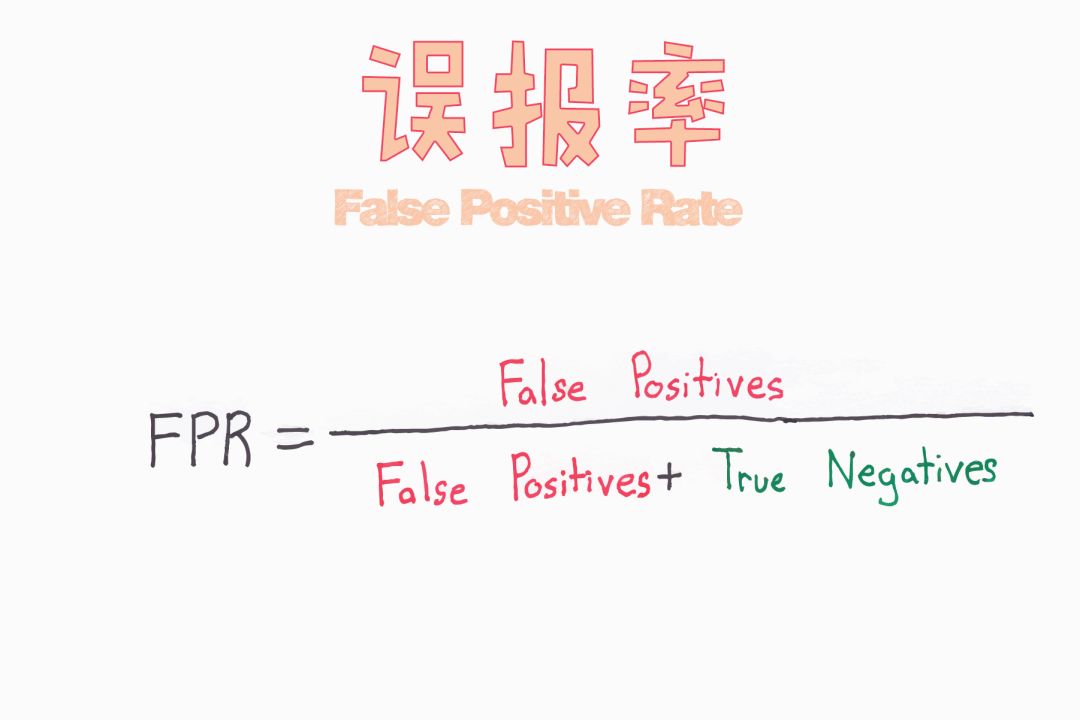
假正例
下面給出一個假正例的例子。比如:模型將一封郵件分類為垃圾郵件(正例),但這封郵件實際并不是垃圾郵件。這就像一個警示,錯誤如果能被修正就更好,但是與假負例相比,它并不是一個嚴重的問題。
作者注:個人觀點,這個例子舉的不太好,對垃圾郵件來說,相比于錯誤地將垃圾郵件分類為正常郵件(假負例),將正常郵件錯誤地分類為垃圾郵件(假正例)是更嚴重的問題。
假正例(I型錯誤)——原假設正確而拒絕原假設。
假負例
假負例的一個例子。例如,該模型預測一封郵件不是垃圾郵件(負例),但實際上這封郵件是垃圾郵件。這就像一個危險的信號,錯誤應該被及早糾正,因為它比假正例更嚴重。
假負例(II型錯誤)——原假設錯誤而接受原假設
上圖能夠很容易地說明上述指標。左圖男士的測試結果是假正例因為男性不能懷孕;右圖女士是假負例因為很明顯她懷孕了。
從混淆矩陣,我們能計算出準確率、精度、召回率和F-1值。
準確率
準確率是模型預測正確的部分。
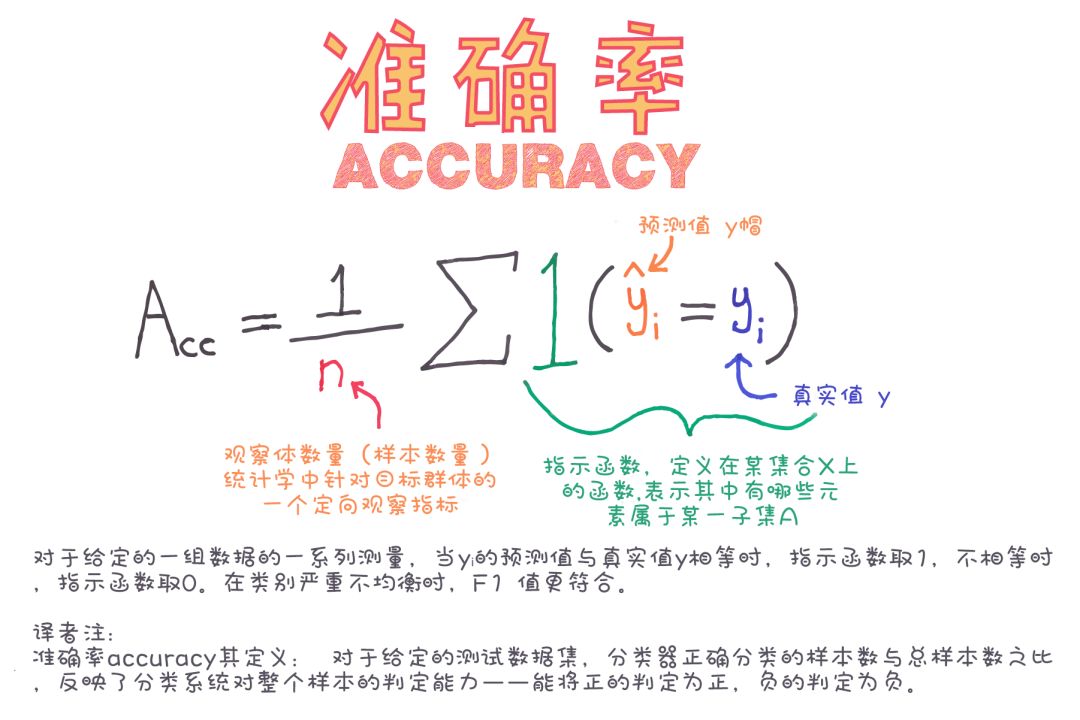
準確率的公式為:
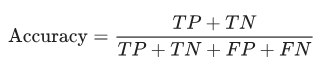
當數據集不平衡,也就是正樣本和負樣本的數量存在顯著差異時,單獨依靠準確率不能評價模型的性能。精度和召回率是衡量不平衡數據集的更好的指標。
精度
精度是指在所有預測為正例的分類中,預測正確的程度為正例的效果。

精度越高越好。
召回率
召回率是指在所有預測為正例(被正確預測為真的和沒被正確預測但為真的)的分類樣本中,召回率是指預測正確的程度。它,也被稱為敏感度或真正率(TPR)。

召回率越高越好。
F-1值
通常實用的做法是將精度和召回率合成一個指標F-1值更好用,特別是當你需要一種簡單的方法來衡量兩個分類器性能時。F-1值是精度和召回率的調和平均值。

普通的通常均值將所有的值平等對待,而調和平均值給予較低的值更高的權重,從而能夠更多地懲罰極端值。所以,如果精度和召回率都很高,則分類器將得到很高的F-1值。
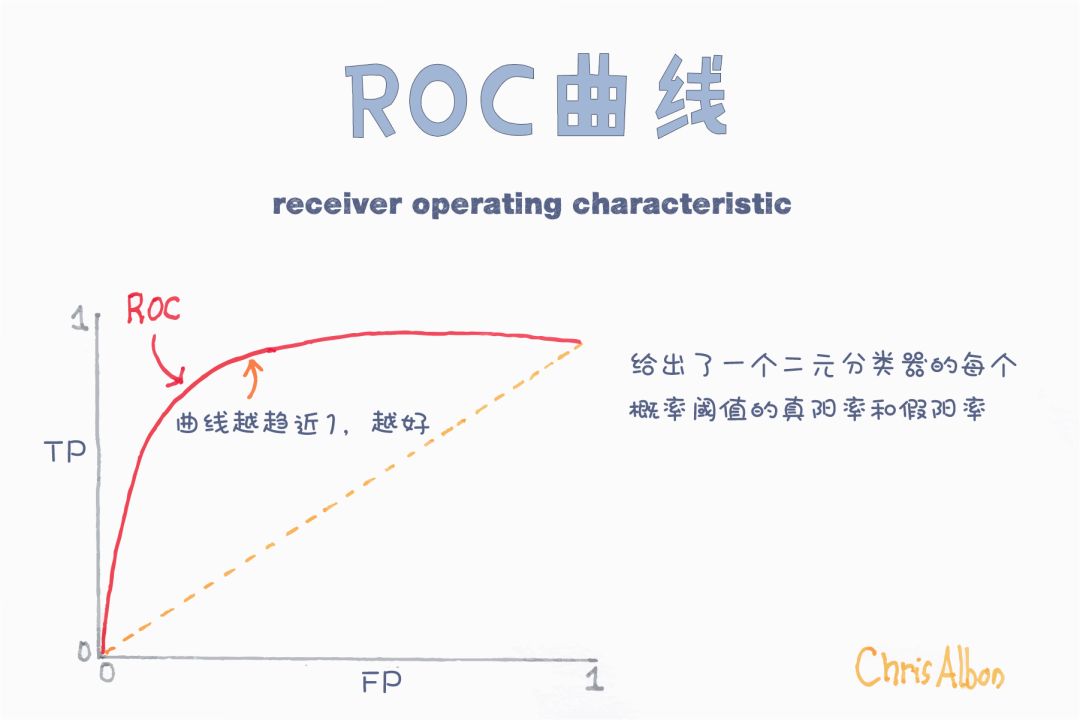
接受者操作曲線(ROC)和曲線下的面積(AUC)
ROC曲線是衡量分類器性能的一個很重要指標,它代表模型準確預測的程度。ROC曲線通過繪制真正率和假正率的關系來衡量分類器的敏感度。如果分類器性能優越,則真正率將增加,曲線下的面積會接近于1.如果分類器類似于隨機猜測,真正率將隨假正率線性增加。AUC值越大,模型效果越好。
累積精度曲線
CAP代表一個模型沿y軸為真正率的累積百分比與沿x軸的該分類樣本累積百分比。CAP不同于接受者操作曲線(ROC,繪制的是真正率與假正率的關系)。與ROC曲線相比,CAP曲線很少使用。
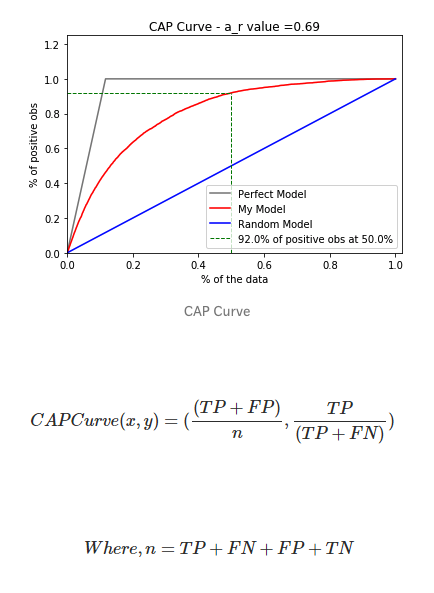
以考慮一個預測客戶是否會購買產品的模型為例,如果隨機選擇客戶,他有50%的概率會購買產品。客戶購買產品的累積數量會線性地增長到對應客戶總量的最大值,這個曲線稱為CAP隨機曲線,為上圖中的藍色線。而一個完美的預測,準確地確定預測了哪些客戶會購買產品,這樣,在所有樣本中只需選擇最少的客戶就能達到最大購買量。這在CAP曲線上產生了一條開始陡峭一旦達到最大值就會維持在1的折線,稱為CAP的完美曲線,也被稱為理想曲線,為上圖中灰色的線。
最后,一個真實的模型應該能盡可能最大化地正確預測,接近于理想模型曲線。
責任編輯:lq
-
數據
+關注
關注
8文章
7134瀏覽量
89402 -
算法
+關注
關注
23文章
4629瀏覽量
93194 -
機器學習
+關注
關注
66文章
8438瀏覽量
132930
原文標題:來!一起捋一捋機器學習分類算法
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
機器人如何實現移動功能

NPU與機器學習算法的關系
利用Matlab函數實現深度學習算法
深度學習中的時間序列分類方法
機器學習算法原理詳解
基于神經網絡的呼吸音分類算法
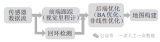
深度解析深度學習下的語義SLAM




 回顧一下機器學習分類算法
回顧一下機器學習分類算法













評論