自動駕駛汽車從A點行駛到B點,需要軌跡規劃算法來進行全局規劃,而具體都有哪些算法呢?這篇文章想和大家分享一下一類最常用的軌跡規劃算法,基于圖搜索的規劃算法。
在開始介紹圖搜索算法之前,先簡單介紹一下自動駕駛中的規劃問題:規劃模塊處于自動駕駛軟件框架中的中間位置,其接收感知、定位、地圖發來的上游信息,輸出一條安全、平穩、舒適的軌跡給到控制模塊,因此起到了一個承上啟下的作用,可以說是影響自動駕駛中舒適性及安全性最重要的一環。而傳統意義上的規劃問題可以分為兩個步驟。
前端負責粗粒度的路徑查找,搜索出一條可行路徑;后端負責細粒度的軌跡生成,生成出一條控制模塊可以很好執行的平滑軌跡。而這篇文章想要探討的,就是前端路徑搜索中一種最常用的方法,基于圖搜索的路徑規劃算法。
圖搜索基礎
圖是數據結構中非常重要的一個概念,包含了節點和邊。在自動駕駛中,通常可以將地圖存儲為柵格地圖,每一格就代表了圖的節點,格與格之間的連線就代表了邊。
上圖展示了一種無向圖,即節點之間的連線是沒有指向的。而在實際場景中,往往每條邊(道路)不僅僅需要考慮距離信息,還需要考慮方向信息、路口擁堵情況、車流量等等,因此自動駕駛中往往構建的為有向圖、權重圖等等。除此之外,合理地對自動駕駛場景下的地圖進行分割也是保證規劃效果的一個很重要的基礎,不能分割太密集導致規劃搜索的效率太低,也不能太粗略從而導致某些場景下明明存在可行解卻無法搜索到。 構建完圖之后,具體的規劃過程其實就是一個搜索的過程,即如何在給定起點及終點的條件下快速搜索出一條滿足期望的最優路徑。在代碼實現上,整個過程需要維護一個容器(container),具體的操作分為三個步驟:移除、擴展、塞入,以此不停循環,直至搜索到終點。下面介紹幾種最常用的搜索算法。
搜索算法DFS & BFS
了解了圖搜索的基礎之后,接下來介紹兩種最基礎的搜索算法:深度優先搜索(DFS)和廣度優先搜索(BFS)。深度優先顧名思義,從起點開始,按照某個順序一條路走下去,直至不能再繼續為止,然后回到上一節點,再換另一條路走下去;而廣度優先則是每一步都擴展同一層的所有可能節點,一層一層擴展下去,直到某一層搜索到終點為止。可以看到深度優先搜索的過程是一條路走到底后,最后訪問的節點最先拿來處理,整個過程可以用棧(stack)來表示,符合“后進先出”的原則;而廣度優先搜索的過程是一層中先訪問的節點拿來處理,可以用隊列(queue)來表示,符合“先進先出”的原則。
那對于搜索算法來說,哪一種算法好一些呢?可以看下下面這張圖,相同的場景下,BFS可以給出一條最短路徑,而DFS雖然速度很快,但隨機性很大,無法給出一條最優路徑,這一缺陷使得我們不得不拋棄DFS,目前的主流基于圖搜索的規劃算法,原理其實都是基于BFS延伸出來的。
但是BFS其實也有一個很嚴重的問題,就是其遍歷的無效節點過多,從而導致搜索效率太慢,上面左圖中的深灰色格點就展示了在搜索過程中,所需要訪問的節點,可以看出大多數的訪問其實都是無用的,不能給最終的搜索提供任何幫助。針對這一缺陷,就引入了Heuristic Search(啟發式搜索),即加入終點信息,從而使得搜索的目標更明確,避免過多的無效搜索。而基于這一改進提出的算法就是GBFS(Greedy Breath-First Search)。
BFS和DPS是根據先入或者后入的順序來選擇要處理的節點,之中不考慮任何終點相關的信息,而GBFS則是將與終點的距離考慮進來,構造一個規則來挑選依次要訪問的節點。與終點的距離有多種形式,最常用的三種為Euclidean Distance、Manhattan Distance以及Diagonal Distance。
舉個例子,在實現BFS算法時,上圖中起點周圍的8個鄰居節點會一起存儲進容器中,由于右上角的節點距離終點更近,因此再彈出時首先彈出該節點,基于該節點再進行擴展,從而加快了搜索效率。從下圖中可以看出,算法過程中所訪問的節點減少了很多,搜索的目標性更加明確,從而極大提升了搜索效率。
Dijkstra算法和A*算法
有了上面的基礎,理解路徑規劃中的Dijkstra和A*算法就很容易了。Dijkstra算法其實BFS的進階版,其可以用于處理帶權重邊的地圖,因此更適合在實際場景中使用。在該算法中,通常采用優先隊列(priority queue)來作為訪問容器,這是由于優先隊列(《key, value》這種形式)可以根據設定的key值自動進行排序,在Dijkstra中key值可以設定為和起點的距離,由于沒考慮和終點的距離信息,因此還不能顯示出優先隊列的優勢,但之后的A*算法里可以看出利用這種結構的方便性。Dijkstra算法的偽代碼如下圖所示:
A*算法和Dijkstra算法的唯一區別就在于優先隊列中排序的依據不同,即key值不同。不同于Dijkstra,A*在存儲節點時,還會考慮和終點的距離(可以類比GBFS之于BFS),其key值計算可以表示為:
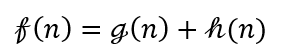
其中即為Heuristic Function,有了這個指向信息,A*算法可以更快地找到終點,避免了許多的無效搜索。其偽代碼如下圖所示:
這里我們可以看出優先隊列的優勢了,我們只需要每次計算的值并將其存儲進優先隊列,它就會自動根據其值進行排序,因此每次就可以取出容器的頂部值即為的最小值。在同一場景下,它們的實際效果如下圖所示,可以看出由于A*避免了許多無效節點的訪問,效率提升很多。 而這又引出了另一個問題,Dijkstra由于無差別的搜索可以保證最短路徑,A*帶有強指向型的搜索方式,能保證結果最優嗎?這其實取決于A*的啟發函數設定,為了保證最優性,需要保證啟發函數是admissible的,即啟發函數的值需要小于等于實際上該點到終點的距離。
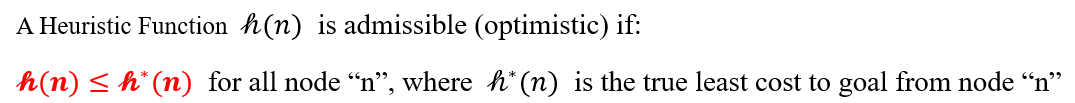
如果啟發式函數是admissible的,那么A*的最終搜索結果就是最優的。其實這也很好理解,因為如果啟發函數的選擇實際上大于到終點的實際距離,那么依據該規則進行的排序搜索,必然會漏掉距離最短的那條路。因此如果我們需要A*給出最短路徑的話,我們可以將啟發函數設定為歐式距離或者對角距離,而不是曼哈頓距離。
以上就是基于圖搜索的常用路徑規劃算法介紹,歡迎大家交流指正。
原文標題:技術|自動駕駛規劃算法解析——圖搜索篇
文章出處:【微信公眾號:汽車工程師】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
AI
+關注
關注
87文章
31490瀏覽量
269914 -
自動駕駛
+關注
關注
784文章
13923瀏覽量
166834
原文標題:技術|自動駕駛規劃算法解析——圖搜索篇
文章出處:【微信號:e700_org,微信公眾號:汽車工程師】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
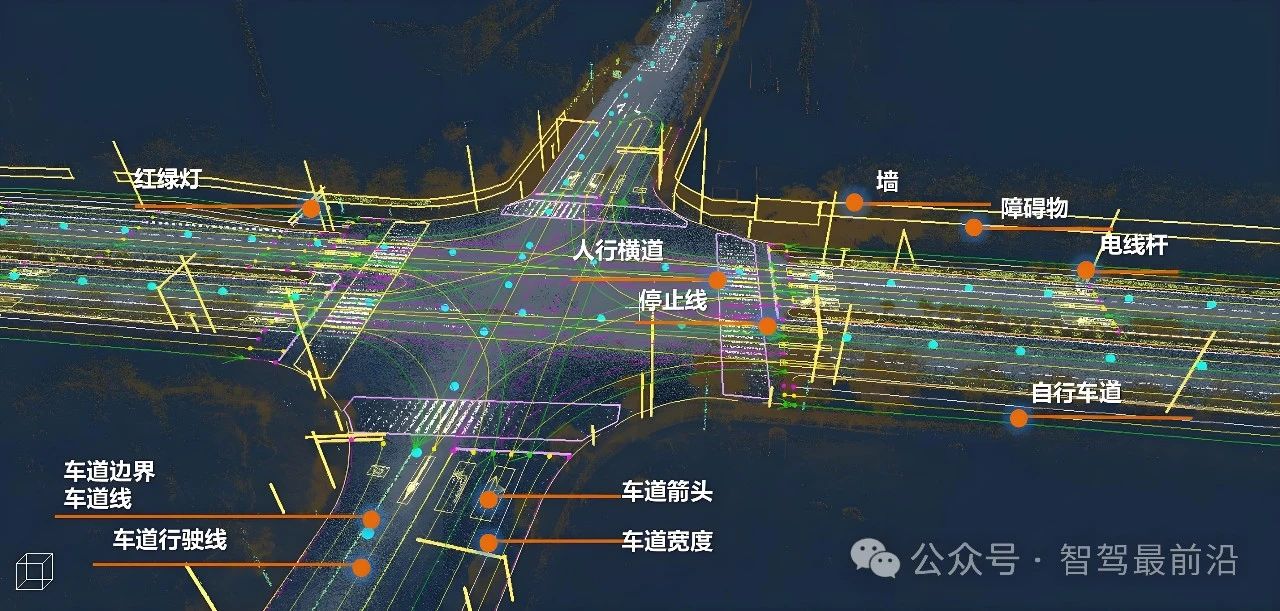
從《自動駕駛地圖數據規范》聊高精地圖在自動駕駛中的重要性
【「具身智能機器人系統」閱讀體驗】2.具身智能機器人的基礎模塊
MEMS技術在自動駕駛汽車中的應用
智能駕駛與自動駕駛的關系


FPGA在自動駕駛領域有哪些優勢?
FPGA在自動駕駛領域有哪些應用?
自動駕駛識別技術有哪些
自動駕駛的傳感器技術介紹
深度學習在自動駕駛中的關鍵技術
未來已來,多傳感器融合感知是自動駕駛破局的關鍵
邊緣計算與自動駕駛系統如何結合
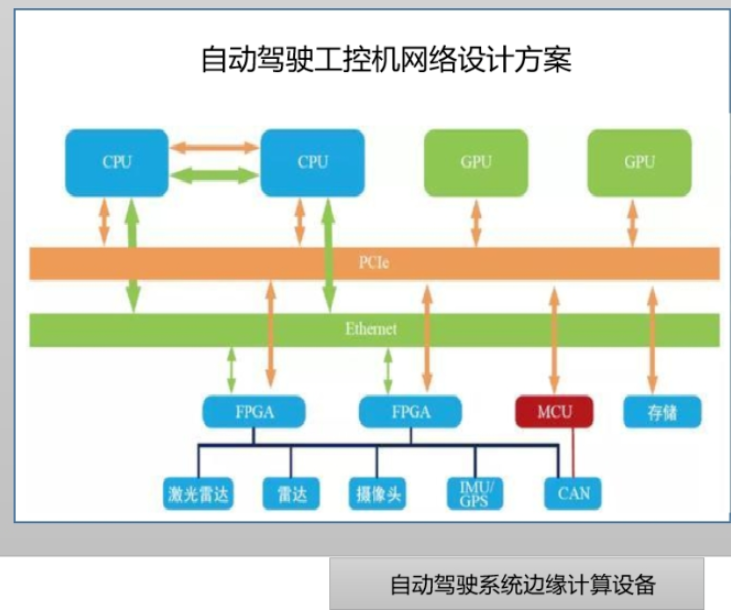




 自動駕駛中基于圖搜索的常用路徑規劃算法介紹
自動駕駛中基于圖搜索的常用路徑規劃算法介紹











評論