導(dǎo)讀
異常檢測(Anomaly Detection), 作為機器學(xué)習(xí)的一個重要分支,實際應(yīng)用領(lǐng)域廣泛,本文作者通過一些有趣的卡通形象作為例子講解了異常檢測入門概念及分類,并通過完整的介紹了如帶標簽與不代表標簽的異常檢測的過程。
Anomaly Detection,也叫做異常檢測,目的在于讓機器知道我所不知道的事情。
1. 什么是 Anomaly(異常)?
雖然說是異常,但其實是以訓(xùn)練集為核心,判斷輸入數(shù)據(jù)是否與訓(xùn)練集中的數(shù)據(jù) “類似”。在不同的領(lǐng)域可以有不同的叫法,比如:outlier Detection,novelty Detection,exceptions Detection。
至于什么才是“類似”,它的定義這取決于你所用的方法。如下圖所示,如果你給的訓(xùn)練集只有雷丘,那么比卡丘就是“異常”;相反,如果你給的訓(xùn)練集是比卡丘,那雷丘就是“異常”。
什么是異常取決于你所給的訓(xùn)練集
1.1 問題定義 Problem Formulation
給定一個訓(xùn)練集
我們要找到一個函數(shù)來檢測 輸入 x 是不是屬于訓(xùn)練集(是否和訓(xùn)練集的數(shù)據(jù)屬于同一類)
用來判斷是否和訓(xùn)練集屬于一類
1.2 為什么不能用二分類來解決這個問題?
如上面所說的,所謂“異常”,其實就是看是否和訓(xùn)練集“相似”,雖然我們很容易獲得正訓(xùn)練集(如上面的雷丘),但是負訓(xùn)練集我們無法來決定,如果我們用 寶可夢 來作為負訓(xùn)練集來訓(xùn)練二分類,那下次輸入一個 亞古獸 呢?這時候二分類模型就無法識別這個沒見過的 負樣本,而這樣的負樣本實在是太多了,我們沒法窮舉。如下圖所示。
負樣本的種類太多反而無法用來訓(xùn)練二分類器
更壞的情況就是,很多情景下,我們沒法收集到負樣本。比如說刷卡行為,大多數(shù)情況都只是正常的交易行為,而盜刷這一類情況就少之又少,甚至(目前)沒有。
所以異常檢測無法簡化成二分類來實現(xiàn),這是一個獨立的研究主題。
1.3 異常檢測模型分類
根據(jù)給出的訓(xùn)練集,我們可以大致將其分成兩大類三小類:
(labeled)訓(xùn)練集中每個樣本都有標簽,用這些樣本來訓(xùn)練一個分類器,這個分類器除了能夠識別訓(xùn)練集中已有樣本標簽外,還能輸出 “unknown” 標簽,用來表示該輸入是“沒見過的”、不在訓(xùn)練集中的。我們把它叫做 “open-set recognition(開放式識別)”
(unlabeled)另一種情況是,我的訓(xùn)練集是沒有標簽的
(clean)但這個訓(xùn)練集是“干凈”的,我們可以將這個訓(xùn)練集里所有的樣本都視為“正樣本“;
(polluted)然而干凈的數(shù)據(jù)集在現(xiàn)實應(yīng)用中很少,大多數(shù)都是或多或少參雜著”異常樣本“,而且你無法知道,比如說銀行給你大量刷卡數(shù)據(jù)進行訓(xùn)練,而這些數(shù)據(jù)里有可能有盜刷的數(shù)據(jù)且沒有標注出來。
異常檢測的兩大類三小類
2. Labeled(帶標簽)
在這里就用 辛普森家族 來舉例子。這里有一堆辛普森家族的人物形象及其對應(yīng)的人物名稱(視為標簽),這樣我們就能訓(xùn)練一個“辛普森角色分類器”,輸入一個人物的形象,輸出該人物的名稱(標簽)。
辛普森家族的人物形象及其名稱標簽,訓(xùn)練一個分類器
那我們訓(xùn)練好“辛普森角色分類器”后,這個分類器會輸出兩類數(shù)據(jù):類別(預(yù)測的名字)、信心值;然后給定一個閾值,當信心度大于這個閾值,就視為“正常值(屬于辛普森家族)”,低于則視為“異常值(不屬于辛普森家族)”
分類器的使用
分類器的輸出其實是一個概率分布(distribution),輸出前經(jīng)過一個softmax,使得這個分布中的值之和為1,其輸出每一項 表示每一個類別及其對應(yīng)的信心值;我們將其中的最大值,視為分類器對該輸入的信心值.
除了最高值,我們還可以用 熵(entropy)來決定分類器最后的信心值。
如下圖所示,第一個分類器中,霸子的信心值很高(總體熵低),且其他很低,就說明分類器能夠很好地把這個人物形象進行分類,故認為該形象是“正常值”;
而第二個分類器中,每一類的信心值都不高且均勻(最大值不高,總體熵高),說明分類器沒見過該形象,信心不夠,沒法很好地區(qū)分,則可以認為該形象是“異常值”。
辛普森家族分類器,輸出了類別和信心度
除了用分類器與其輸出的分布來 判斷 該分類器的信心度,當然還有其他的方式,如下圖所說的,不僅輸出分布(用來分類),還教分類器直接輸出其信心度(直接可以判斷是否異常)。
可以直接輸出分類和信心值的分類器
關(guān)于上面模型訓(xùn)練部分,一般來說我們有個“驗證集”來調(diào)節(jié)模型的超參數(shù),在“訓(xùn)練集”中,所有的樣本都是“正樣本“且有各自的標簽(如都是辛普森和他們的人物名字),而在”驗證集“中就沒必要每個樣本都有其“人物標簽”,只需要判斷其“是否屬于辛普森家族”就行了(兩個標簽:屬于、不屬于)。
2.1 評價標準
在上面的例子中,“辛普森家族異常檢測模型“其實是一個普通分類器,那我們是否也可以用準確率(Accuracy)來評估這個模型的好壞呢?答案是:這不是一個好的選擇。
正如我們前面所說的,異常檢測的數(shù)據(jù)集的標簽分布是不均勻的,也就是說我們很大概率能夠找到“正樣本”而缺少“負樣本”;這種情況下,如果模型“無情地”把所有的樣本都預(yù)測成正樣本,那準確率也會很高,這樣顯然是不對的。
在這里,只有5張“異常圖片”,模型準確率卻很高
準確率對于不平衡數(shù)據(jù)沒法很好地評估,其實也有很多方法來解決,比如說成本積分制:當正常數(shù)據(jù)沒有檢測出,則成本為100,異常數(shù)據(jù)沒有檢測出,成本為1(見Cost Table A),這時候左邊模型的成本則會低于右邊模型的成本(紅色字體),則左邊的模型更優(yōu)秀;而如果正常數(shù)據(jù)沒檢測出的成本為1,異常數(shù)據(jù)沒檢測出的成本為100,這時候右邊的模型就更優(yōu)秀(藍色字體);
積分制的使用要取決于你對業(yè)務(wù)的理解:異常數(shù)據(jù)沒檢測出、正常數(shù)據(jù)沒檢測出,哪個更加重要?比如在醫(yī)療上,對于癌細胞的異常檢測,寧愿檢測錯正常人,也不要漏過一個病人,這時候“異常數(shù)據(jù)沒檢測出的成本更高”。
除了積分制,還有很多方法,比如AUC、Macro-F1等等。
積分制,左邊模型和右邊模型誰更優(yōu)秀取決于Cost Table的定制
2.2 存在的問題
分類器也許可以能夠?qū)Α耙话惝惓!边M行“識別”,比如下面貓狗的分類器,就能夠把羊駝和馬來貘識別為“異常”,然而有一些“異常數(shù)據(jù)”則沒那么容易了,比如說老虎和狼,這就是模型泛化問題;
因為模型一般只會抽取出一類圖片中的共同特征,而此時“異常數(shù)據(jù)”無意中也具備了這一共同特征,那么就會出現(xiàn)把狼識別成狗的情況了。
下面的模型把老虎識別成貓,把狼識別成狗
另一個例子就是上面的“辛普森家族分類器”,將人物涂黃后,模型就會進一步識別成“麗莎”,這就說明了模型識別麗莎靠的是顏色,這顯然是不正確的。
圖片涂改后,就會識別成其他人物
針對以上存在的問題,也有很多工作試圖去解決,比如說收集一些“異常數(shù)據(jù)”,讓分類器去學(xué)習(xí)給它們更低的信心值;然而我們一開始就說了,異常數(shù)據(jù)很難獲取,那我們就想:能不能自動生成“異常數(shù)據(jù)”?
這時候我們就可以用GAN來嘗試生成“有點像正常數(shù)據(jù)卻又沒那么像”的異常數(shù)據(jù)。
下面給出了相關(guān)文獻,有興趣的可以去了解一下。
解決該問題的相關(guān)文獻
3. Without Labels(不帶標簽的)
這一部分,就是得到了沒有標簽的數(shù)據(jù)。該問題的定義和帶標簽的分類器一樣,都是根據(jù)訓(xùn)練集訓(xùn)練模型,然后幫我分析輸入數(shù)據(jù)相較于訓(xùn)練集是否屬于異常數(shù)據(jù)。與分類器給出的信心值不同,這一類的模型給出的是一個概率,如果概率大于某個閾值,才認為是正常值;
在這一部分,用一個游戲舉個例子:Twitch Plays Pokemon。這個游戲是一個多人同時“玩一個角色”的在線游戲,然而和我們平時玩的網(wǎng)游不一樣,在這個游戲中,下一步動作取決于所有在線用戶的操作(如下圖的右邊,是每一個用戶按下的指令)。
眾多用戶的指令靠某種機制共同決定游戲角色下一步操作
然而玩這個游戲的人非常崩潰,因為這個游戲很難進行下去(因為要所有在線玩家都給一個角色發(fā)送指令,而每個玩家的指令又不相同,而游戲只會執(zhí)行其中一個指令)。所以玩家們就在想:是不是有些“惡意玩家”在亂發(fā)送指令,阻止游戲進程?也就是說是不是有人不想讓這個游戲結(jié)束。
這樣我們就有需求——找出“惡意用戶”。在這之前,我們先有個假設(shè):大部分玩家都希望完成這個游戲(也就是說大部分都是正常數(shù)據(jù)),而這部分數(shù)據(jù)我們會用來訓(xùn)練。然后我們使用異常檢測,找出其中的“惡意玩家”(異常數(shù)據(jù))。
由該游戲產(chǎn)生的思考
接下來,我們就要對其進行建模。在這里,我們的需求是把一堆“無標簽”玩家分為正常用戶和異常用戶,這時我們需要把用戶表示成一個向量,這樣才能輸入進我們的模型;而向量中的每一項可以表示這個用戶的一種行為。
如下圖,表示這個用戶過去一段時間內(nèi)說垃圾話的頻率(垃圾話是指游戲指令之外的話,多余的,不影響游戲進程),表示的是這個用戶過去一段時間內(nèi),隨機機制下的發(fā)言頻率。
這個游戲有兩種機制:投票機制和隨機機制 投票機制:20秒內(nèi)最多玩家輸入的指令,則作為游戲下一步的指令;隨機機制:隨機選擇在線玩家輸入的指令,作為游戲下一步的指令。
用向量表示用戶
輸入定義好了,我們就可以看看輸出:模型會輸出一個概率,和分類器不一樣,無標簽訓(xùn)練模型沒有對應(yīng)的Y值(標簽)和信心值,只會輸出一個概率;而和分類器相似的是,我們一樣有一個,當時,視為正常數(shù)據(jù);當時,視為異常數(shù)據(jù)。如下圖所示。
輸出一個概率值,需要設(shè)定一個閾值
假設(shè)我們現(xiàn)在已經(jīng)獲取了大量用戶的數(shù)據(jù),下圖是這些數(shù)據(jù)可視化展示。從可視化中可以獲得一些信息:
在隨機機制下,用戶就越喜歡發(fā)指令(左上圖);
大部分用戶都會或多或少地亂輸入指令(說垃圾話,右下圖)。
這時候,我們就可以很直觀地看到,但用戶落在左上角的位置,則很大可能這就是一個“正常玩家”,而用戶落在靠右或者靠下的位置,則很大可能是“異常玩家”。
已知用戶行為數(shù)據(jù)的可視化圖
然而,我們需要一個數(shù)值化的表示方法,給每一個玩家一個分數(shù)。
假設(shè)我們之前看到的圖,圖上面所有的點都是由一個概率密度函數(shù)生成的(不懂也沒關(guān)系,就當它是一個函數(shù)就行了),是該函數(shù)的參數(shù),決定了這個函數(shù)“長什么樣”,是未知的,需要從數(shù)據(jù)中學(xué)習(xí)。
而我們的工作就變成了:它究竟長什么樣?這時候我們就需要一個“Likelihood”的概念,意思就是說,根據(jù)我們的概率密度函數(shù),能夠產(chǎn)生這樣的已知數(shù)據(jù)的概率有多大。
如果嚴格來說,輸出的不是概率,而是概率密度,它的值也不是介于0~1之間,而是有可能大于1的。在這里,為了簡化問題,我們簡單地認為是概率就好。
而這個“Likelihood”要怎么算呢,它其實就等于每項已知數(shù)據(jù)根據(jù)這個函數(shù)所產(chǎn)生出來的概率的乘積;于是我們就有下面這條公式,很顯然,這個公式是由來控制的,不同的,就會有不同的,就會算出不同的“Likelihood”
這時候,我們并不知道是多少,但我們知道,這個,能夠使我們的“Likelihood”最大化
我們使用Likelihood來訓(xùn)練模型
上面是只是一個抽象的說法。在這里,我們?yōu)榱俗尨蠹腋美斫猓覀兙图僭O(shè)概率密度函數(shù)為常用的高斯分布(Gaussian Distribution),這個概率密度函數(shù)并不簡單,大家看不懂也沒關(guān)系,就當它是一個普通函數(shù)就可以了,輸入一個向量x,輸出這個x被采樣到的概率;而我們前面提到需要學(xué)習(xí)的,在這里就等于這里需要學(xué)習(xí)的均值和協(xié)方差矩陣
為什么這里選擇高斯分布?
其實這只是舉例子,甚至可以是一個神經(jīng)網(wǎng)絡(luò),而此時就是神經(jīng)網(wǎng)絡(luò)的參數(shù),所以我們沒必要在這里糾結(jié),我們只需要清楚無標簽時,異常檢測是如何處理的,從而觸類旁通。
高斯分布,及其需要學(xué)習(xí)的參數(shù)
這時候,Likelihood方程就會置換成下圖的形式,用來找出能使Likelihood最大化的和。
左圖給了一個很好的示例,告訴我們,的取值,如何影響Likelihood的取值;左上角時,數(shù)據(jù)落在這個區(qū)域的概率就很大,這時候Likelihood就很大,而右下角時,落在這個區(qū)域的概率就小,這是Likelihood就小。
和其實是有公式算出來的,就是所有的訓(xùn)練數(shù)據(jù)的向量做一個平均(輸入向量是二維的,所以也是二維的),而就看圖的右下角這個公式,這里很簡單。
抽象的概念替換為具體的高斯分布時的計算方法
在這里,我們已經(jīng)得到了和,我們可以用來做異常檢測,我們把測試數(shù)據(jù)代入我們的高斯分布方程,我們就能算出其概率,如果這個概率大于閾值,是認為是正常值,否則視為異常值。
如果我們用這個訓(xùn)練好的方程,大概就是下圖右下角的樣子,顏色越深代表這個方程輸出的數(shù)值就越大,就越代表“正常玩家”,而顏色越淺越藍的,就代表“異常玩家”;而這個閾值,其實其中一條等高線;右下圖就給出了正常點和異常點的位置示意。
根據(jù)公式,可以獲得其對應(yīng)的概率,從而判斷是否異常
以上的例子,我們只是使用了兩個特征,也就是輸入向量x只是二維;而機器學(xué)習(xí)的好處就是可以處理更多特征,只要你想到的,都可以加進去。下圖就增加到5個特征,再訓(xùn)練一個Likelihood,從而獲得“更準確的”異常檢測效果。
我們可以添加更多的特征
3.1 更多的方法
除了上面的方法,還有一種常用方法是:Auto-encoder(自動編碼器),如下圖所示,Encoder(編碼器)先把辛普森的照片編碼成一個code(隱含層),然后Decoder(解碼器)把code解碼回原來的的照片,訓(xùn)練時會同時訓(xùn)練編碼器和解碼器,盡量讓解碼后的照片和原照片盡可能相似(甚至相同)。這時候如果用Auto-encoder來識別一張“異常圖片”,這時候的解碼器是無法重構(gòu)回原來的照片,通過計算重構(gòu)后的照片和原照片的“距離”(或者說是相似度、還原度),就可以區(qū)分該照片是不是“異常值”。
在我看來,Auto-encoder比分類器多了一重保障(指Decoder解碼器),在分類器上,找到對應(yīng)的特征,就進行判斷,比如顏色、輪廓等等,上面就有例子說明這樣的情況并不可靠;而解碼器就是一種利用特征的過程,我利用編碼器提取的特征,看是否能夠重構(gòu)回原來照片,就能知道這是不是異常值;
自動編碼器的工作流程
下圖是正常的圖片,可以看到模型很容易就重構(gòu)了回來,而且和原圖非常接近。因為這個模型看過辛普森,所以非常“擅長”還原辛普森。
辛普森家族的照片就能很好地復(fù)原
如下圖的Testing階段,對比原圖和重構(gòu)圖,我們可以看到,編碼器提取到的應(yīng)該是“黃色”和“棕色”這兩個特征,然而編碼器用兩個特征構(gòu)建出來的圖片,顯然和原圖相差甚遠,這時候就可以識別為“異常值”。(從重構(gòu)圖可以隱約看到,這大概也是一個辛普森角色)
其他圖片就會復(fù)原到模型所“理解”到的辛普森角色形象
除了自動編碼器,還有很多其他模型可以做這樣的事,比如one-class SVM,Isolated Forest。有興趣的可以自行進一步學(xué)習(xí)。
更多的模型
4. 應(yīng)用
異常檢測的應(yīng)用非常廣泛,下面幾項是非常常見的:
Fraud Detection(欺詐識別)
訓(xùn)練集:正常的刷卡行為;輸入x:盜刷行為?
Network Intrusion Detection(網(wǎng)絡(luò)入侵檢測)
訓(xùn)練集:正常的訪問;輸入x:攻擊行為?
Cancer Detection(癌癥檢測)
訓(xùn)練集:正常細胞;輸入x:癌細胞
責任編輯:lq
-
異常檢測
+關(guān)注
關(guān)注
1文章
42瀏覽量
9751 -
分類器
+關(guān)注
關(guān)注
0文章
152瀏覽量
13211 -
機器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8438瀏覽量
132927
原文標題:異常檢測(Anomaly Detection)到底是什么?
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
村田電容標簽材質(zhì)代碼如何看?

今天給大家演示一下ABS抗金屬資產(chǎn)管理標簽的應(yīng)用 #抗金屬標簽 #資產(chǎn)管理標簽
RFID耐高溫標簽的選型要素及常見應(yīng)用產(chǎn)品推薦
物聯(lián)網(wǎng)系統(tǒng)中非接觸近場通信方案NFC詳解(一)_NFC標簽分析
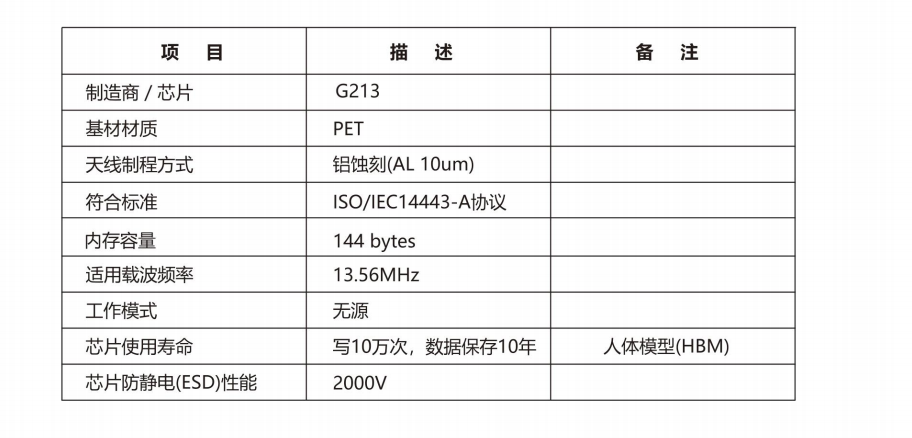
如何選用RFID標簽打印機
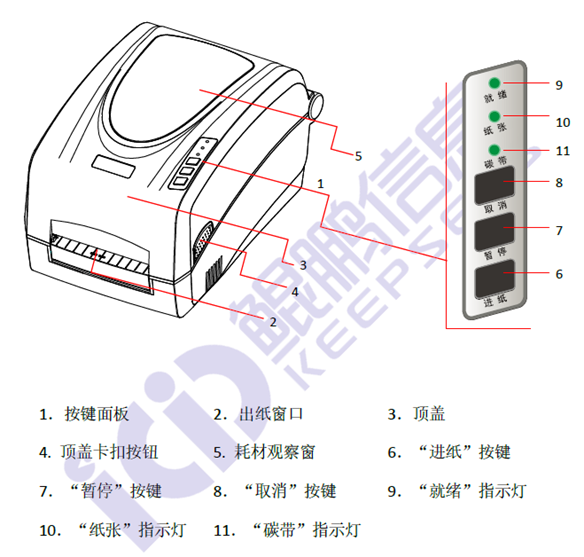
rfid標簽具有哪些顯著的優(yōu)點?
RFID軍標亮燈標簽,智能高效新體驗!
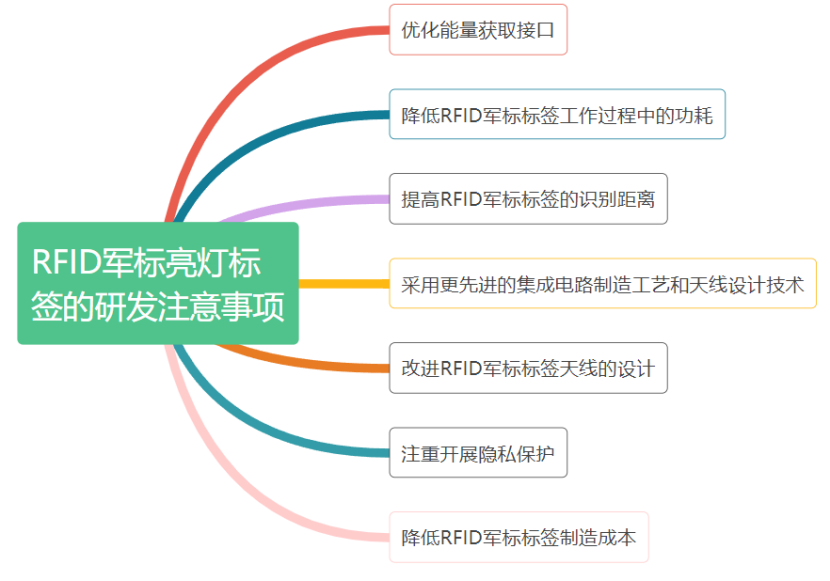
一文介紹:UWB定位標簽種類及選擇

產(chǎn)品標簽OCR識別缺陷檢測系統(tǒng)方案


今日開展|融智興科技與您相約2024中國國際標簽展 #展會 #電子標簽 #RFID #rfid標簽
什么是藍牙資產(chǎn)標簽?

藍牙資產(chǎn)標簽信標

rfid標簽分為幾類,各有什么特點





 如帶標簽與不代表標簽的異常檢測的過程
如帶標簽與不代表標簽的異常檢測的過程











評論