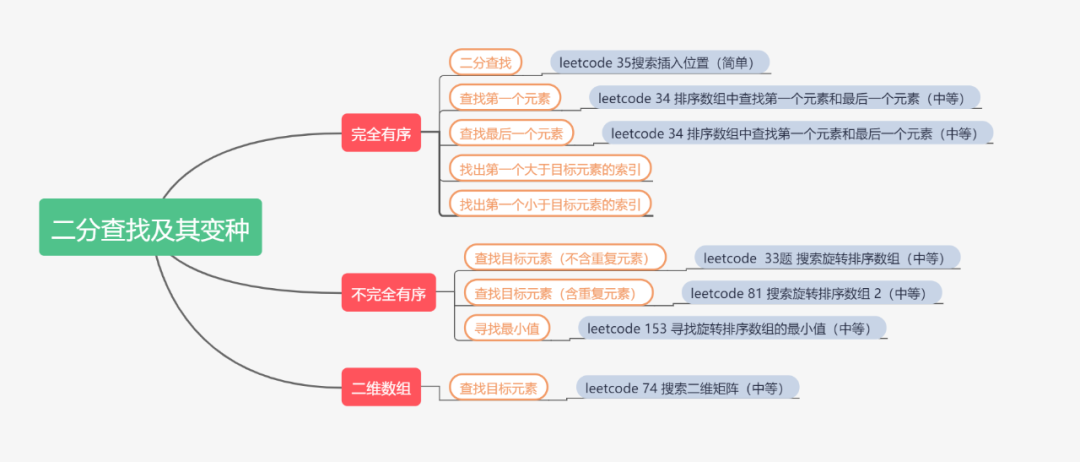
今天給大家帶來的是二分查找及其變種的總結,大家一定要看到最后呀,非常非常用心的一篇文章,廢話不多說,讓導演幫我們把鏡頭切到袁記菜館吧!
袁記菜館內。。。。
店小二:掌柜的,您進貨回來了呀,喲!今天您買這魚挺大呀!
袁廚:那是,這是我今天從咱們江邊買的,之前一直去菜市場買,那里的老貴了,你猜猜我今天買的多少錢一條。
店小二:之前的魚,30個銅板一條,今天的我猜26個銅板。
袁廚:貴了。
店小二:還貴呀!那我猜20個銅板!
袁廚:還是貴了。
店小二:15個銅板。
袁廚:便宜了
店小二:18個銅板
袁廚:恭喜你猜對了
上面的例子就用到了我們的二分查找思想,如果你玩過類似的游戲,那二分查找理解起來肯定很輕松啦,下面我們一起征服二分查找吧!
完全有序
二分查找
二分查找也稱折半查找(Binary Search),是一種在有序數組中查找某一特定元素的搜索算法。我們可以從定義可知,運用二分搜索的前提是數組必須是有序的,這里需要注意的是,我們的輸入不一定是數組,也可以是數組中某一區間的起始位置和終止位置
通過上面二分查找的定義,我們知道了二分查找算法的作用及要求,那么該算法的具體執行過程是怎樣的呢?
下面我們通過一個例子來幫助我們理解。我們需要在 nums 數組中,查詢元素 8 的索引

(1)我們需要定義兩個指針分別指向數組的頭部及尾部,這是我們在整個數組中查詢的情況,當我們在數組某一區間進行查詢時,可以輸入數組,起始位置,終止位置進行查詢。
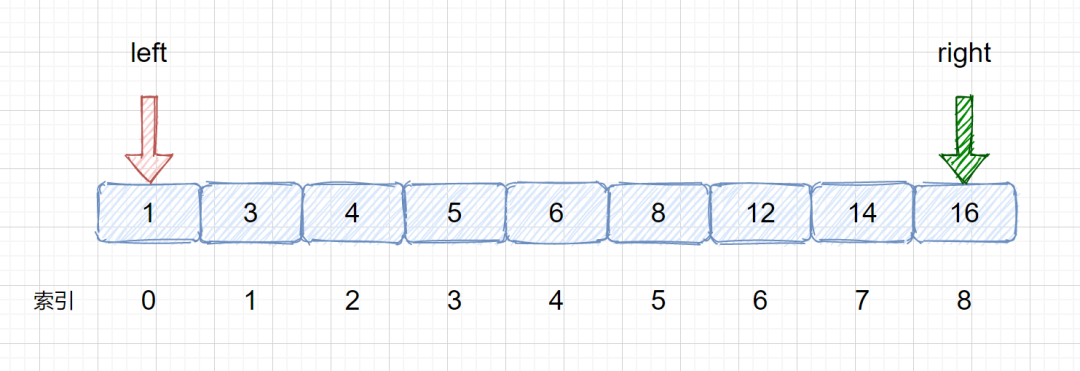
(2)找出mid,該索引為mid =(left + right)/ 2,但是這樣寫有可能溢出,所以我們需要改進一下寫成mid = left +(right - left)/ 2 或者 left + ((right - left ) >> 1) 兩者作用是一樣的,都是為了找到兩指針的中間索引,使用位運算的速度更快。那么此時的 mid = 0 + (8-0) / 2 = 4
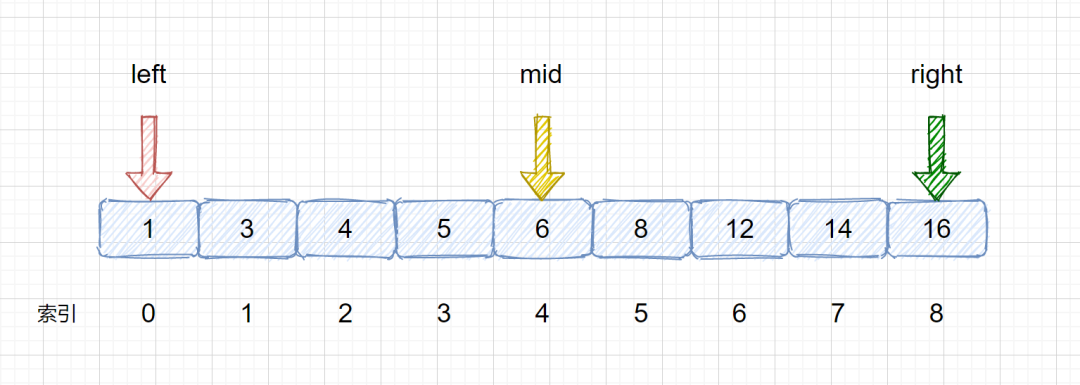
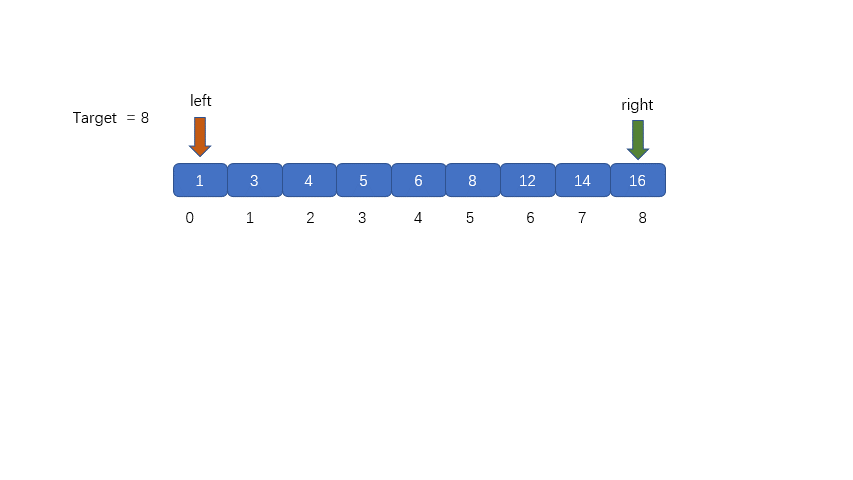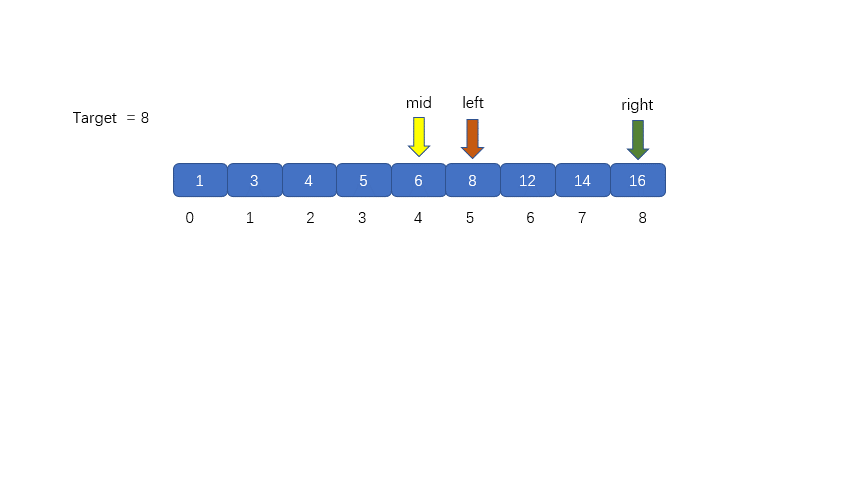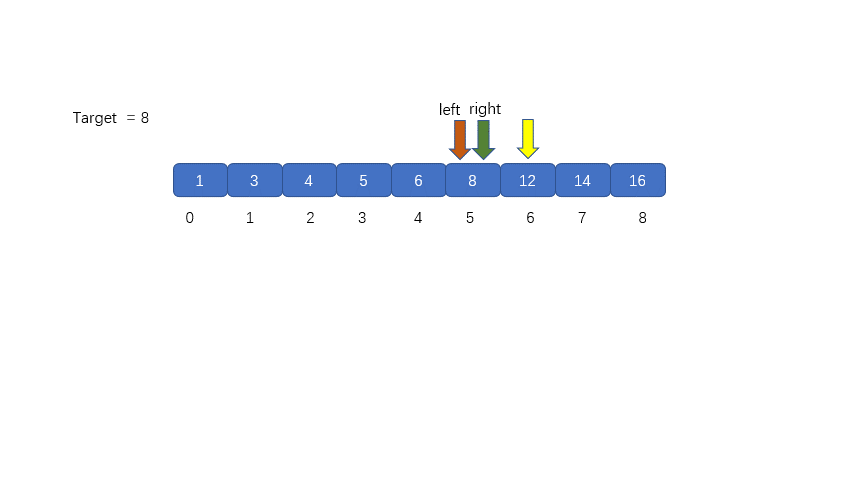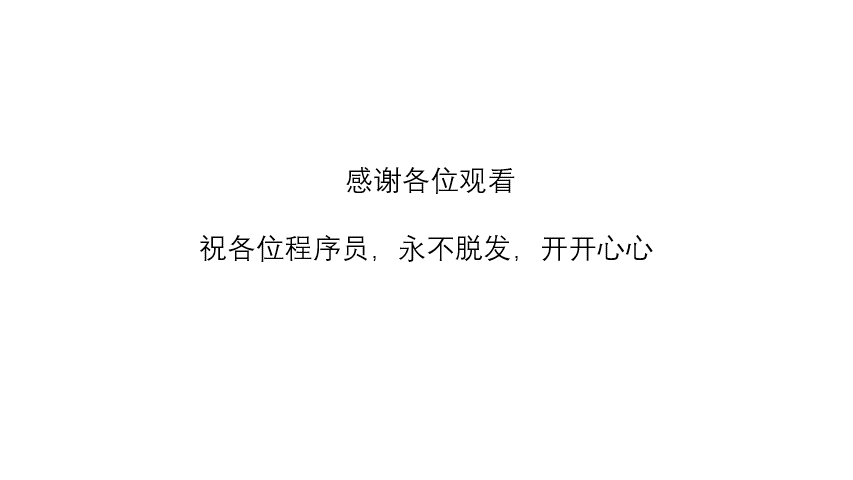
(3)此時我們的 mid = 4,nums[mid] = 6 < target,那么我們需要移動我們的 left 指針,讓left = mid + 1,下次則可以在新的 left 和 right 區間內搜索目標值,下圖為移動前和移動后
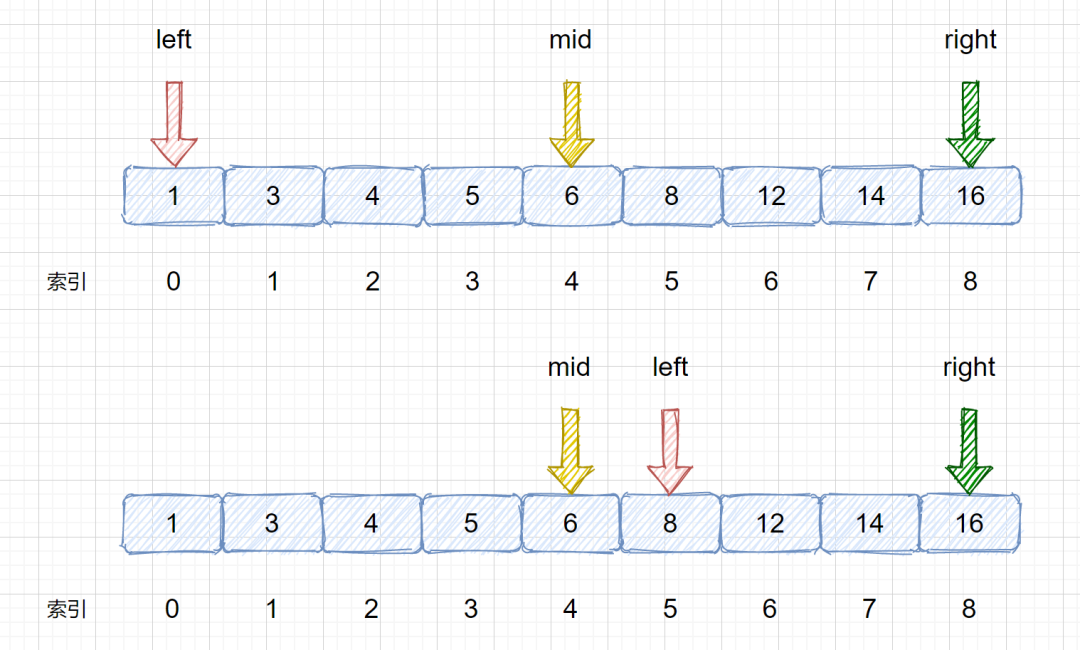
(4)我們需要在 left 和 right 之間計算 mid 值,mid = 5 + (8 - 5)/ 2 = 6 然后將 nums[mid] 與 target 繼續比較,進而決定下次移動left 指針還是 right 指針,見下圖
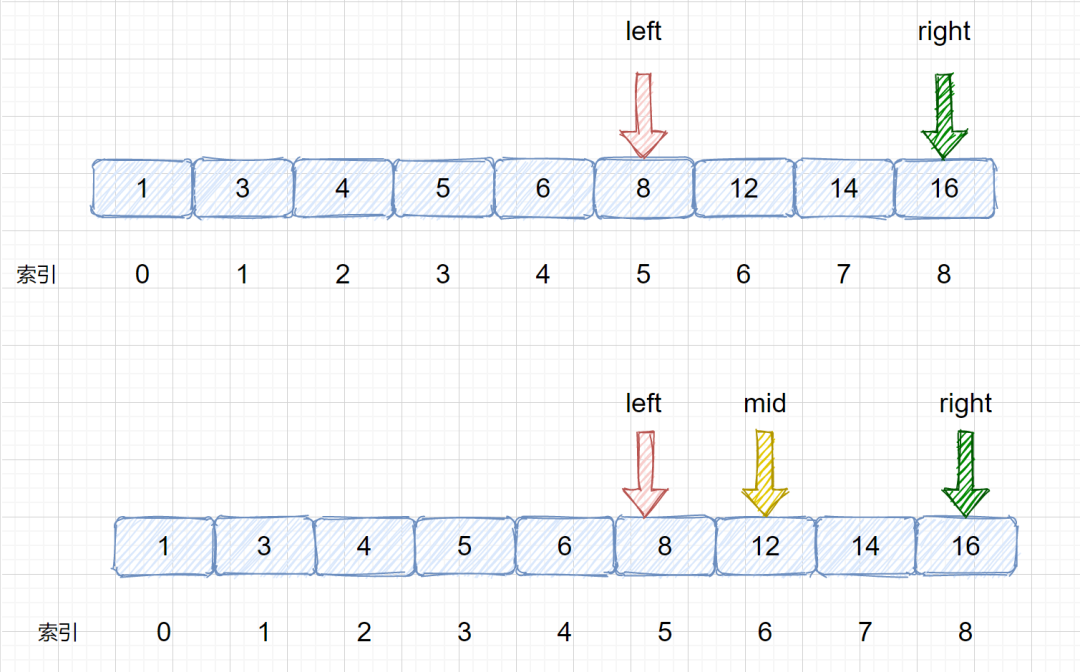
(5)我們發現 nums[mid] > target,則需要移動我們的 right 指針, 則 right = mid - 1;則移動過后我們的 left 和 right 會重合,這里是我們的一個重點大家需要注意一下,后面會對此做詳細敘述。
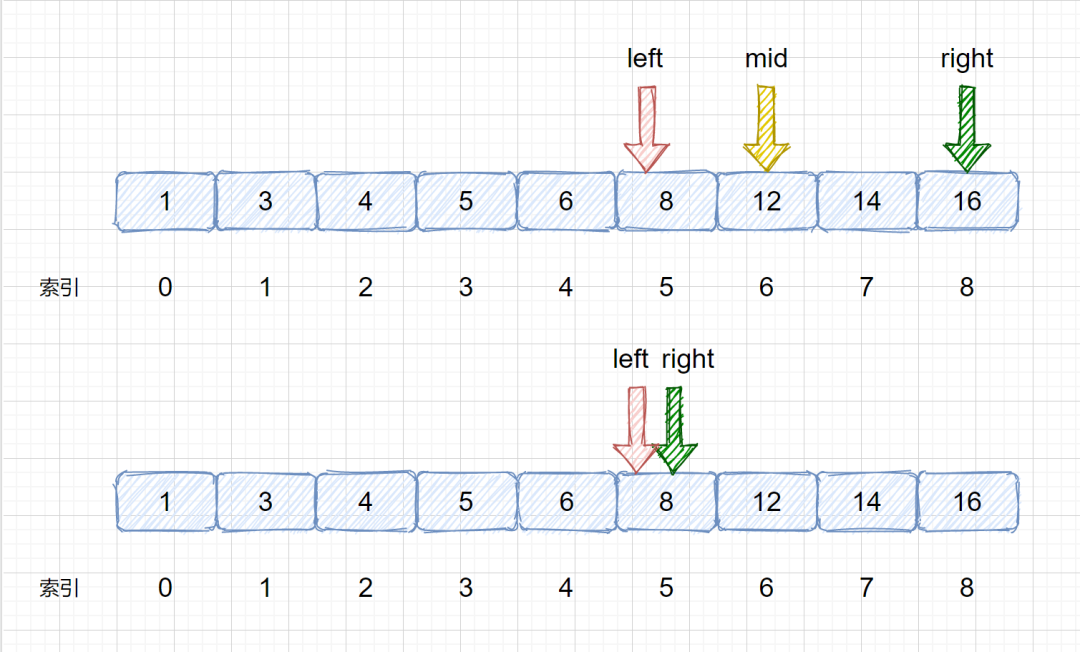
(6)我們需要在 left 和 right 之間繼續計算 mid 值,則 mid = 5 +(5 - 5)/ 2 = 5 ,見下圖,此時我們將 nums[mid] 和 target 比較,則發現兩值相等,返回 mid 即可 ,如果不相等則跳出循環,返回 -1。
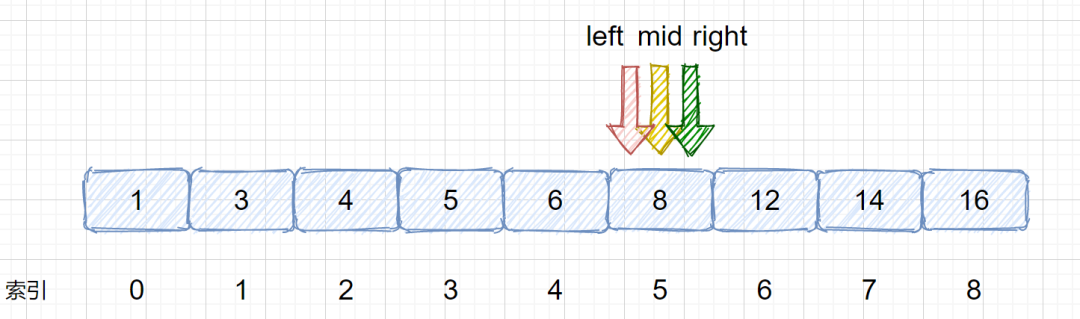
二分查找的執行過程如下
1.從已經排好序的數組或區間中,取出中間位置的元素,將其與我們的目標值進行比較,判斷是否相等,如果相等則返回。
2.如果nums[mid] 和 target 不相等,則對 nums[mid] 和 target 值進行比較大小,通過比較結果決定是從 mid的左半部分還是右半部分繼續搜索。
如果 target > nums[mid] 則右半區間繼續進行搜索,即 left = mid + 1;若target < ?nums[mid] 則在左半區間繼續進行搜索,即 right = mid -1;
動圖解析
下面我們來看一下二分查找的代碼,可以認真思考一下 if 語句的條件,每個都沒有簡寫。
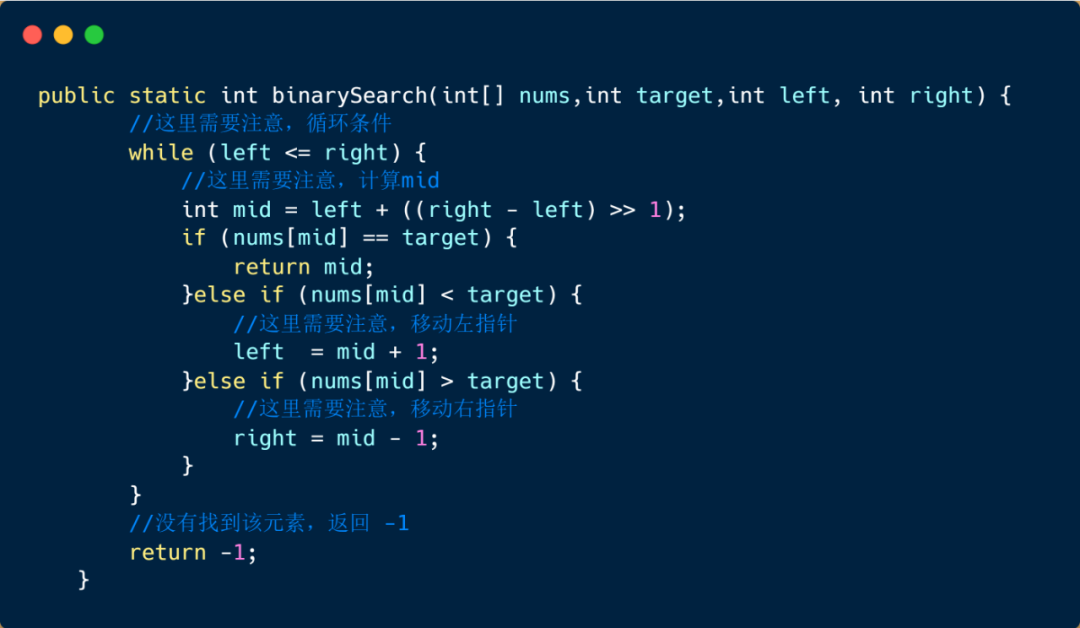
二分查找的思路及代碼已經理解了,那么我們來看一下實現時容易出錯的地方
1.計算 mid 時,不能使用 (left + right )/ 2,否則有可能會導致溢出
2. while (left < = right) ?注意括號內為 left <= right?,而不是 left < right ,我們繼續回顧剛才的例子,如果我們設置條件為 left ?< ?right 則當我們執行到最后一步時,則我們的 left 和 right 重疊時,則會跳出循環,返回 -1,區間內不存在該元素,但是不是這樣的,我們的 left 和 right 此時指向的就是我們的目標元素 ,但是此時 left = right 跳出循環
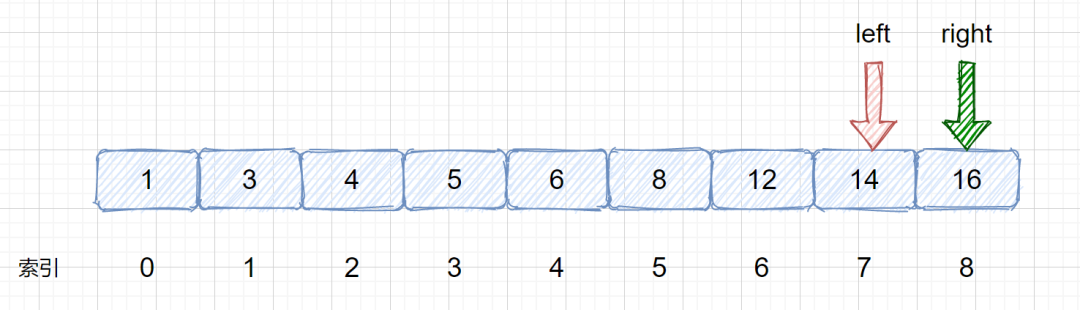
3.left = mid + 1,right = mid - 1而不是 left = mid 和 right = mid。我們思考一下這種情況,見下圖,當我們的target 元素為 16 時,然后我們此時 left = 7 ,right = 8,mid = left + (right - left) = 7 + (8-7) = 7,那如果設置 left = mid 的話,則會進入死循環,mid 值一直為7 。
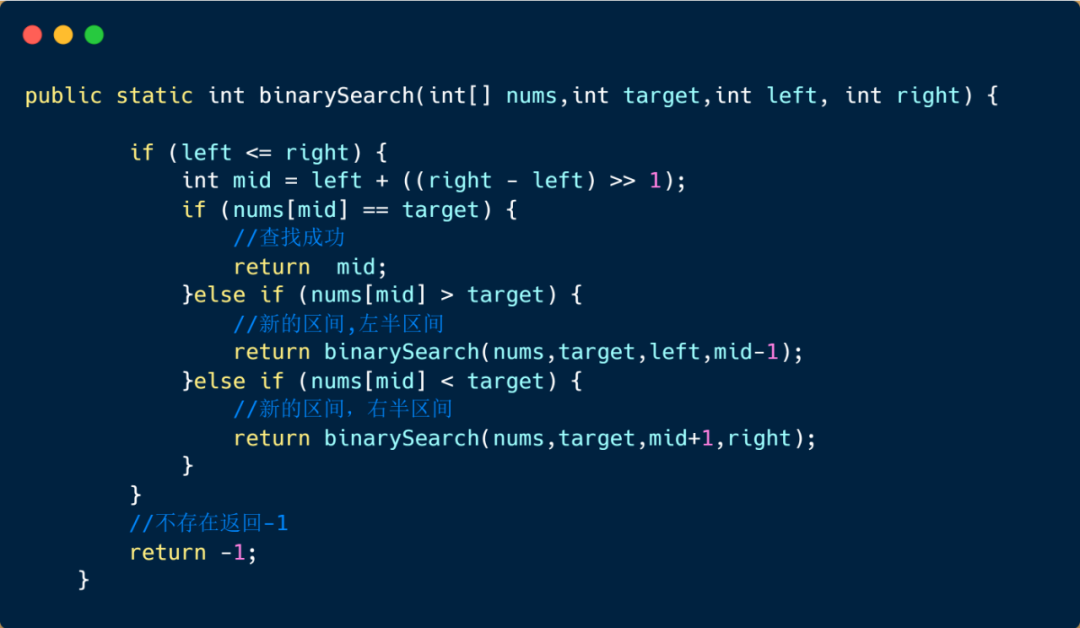
下面我們來看一下二分查找的遞歸寫法
leetcode35搜索插入位置
題目描述
給定一個排序數組和一個目標值,在數組中找到目標值,并返回其索引。如果目標值不存在于數組中,返回它將會被按順序插入的位置。
你可以假設數組中無重復元素。
示例 1:
輸入: [1,3,5,6], 5 輸出: 2
示例 2:
輸入: [1,3,5,6], 2 輸出: 1
示例 3:
輸入: [1,3,5,6], 7 輸出: 4
示例 4:
輸入: [1,3,5,6], 0 輸出: 0
題目解析
這個題目完全就和咱們的二分查找一樣,只不過有了一點改寫,那就是將咱們的返回值改成了 left,具體實現過程見下圖
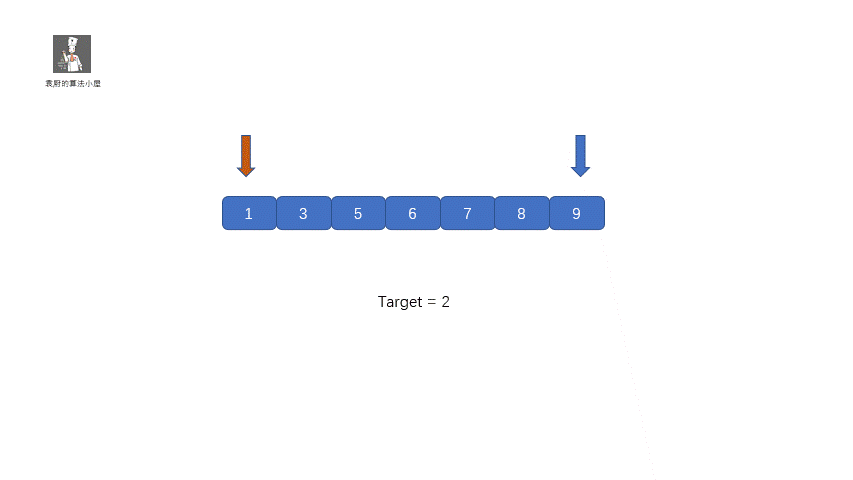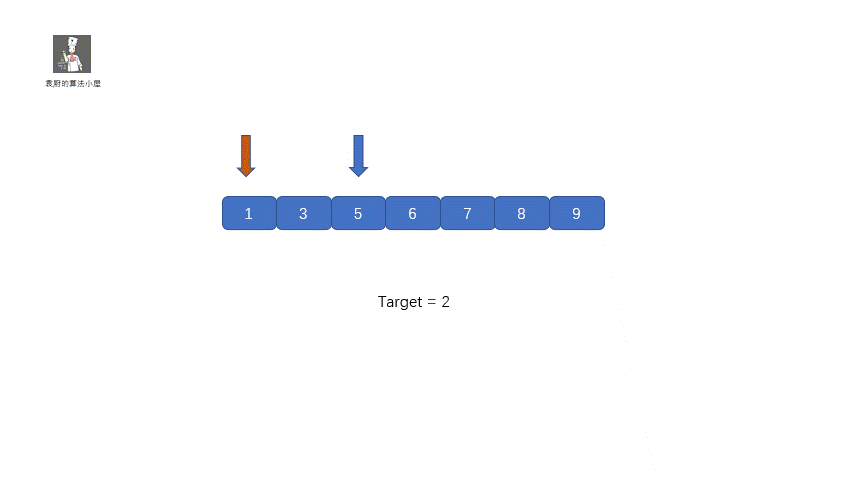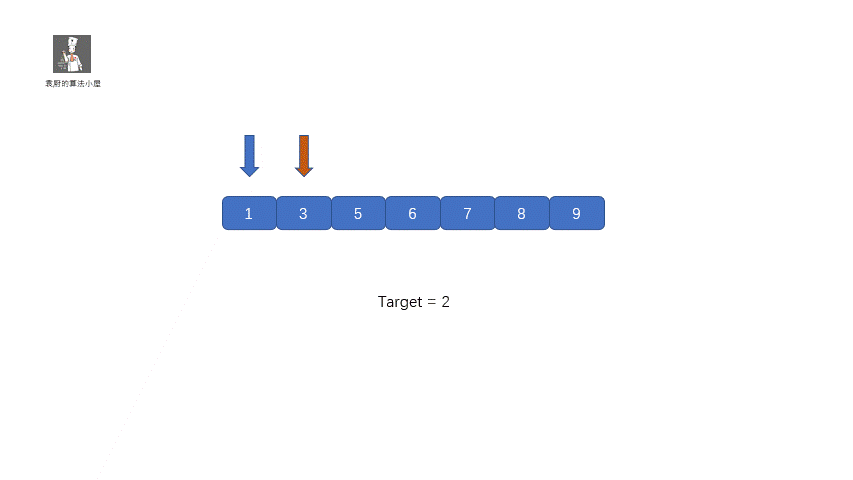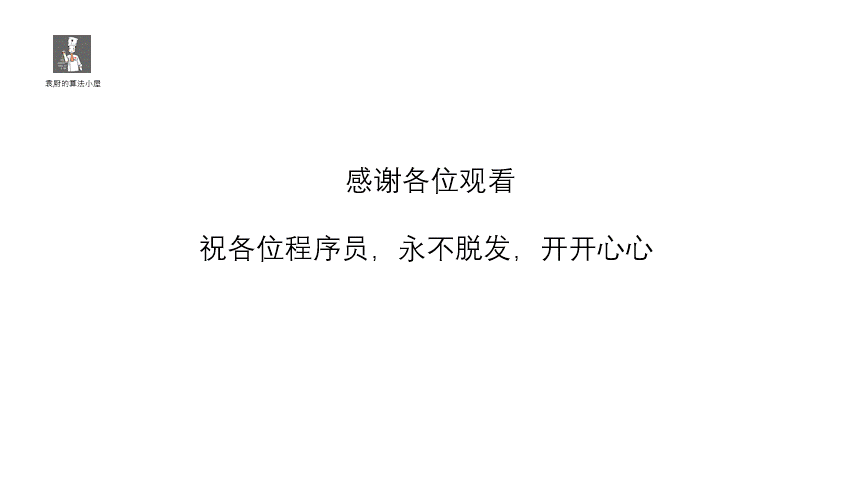
題目代碼
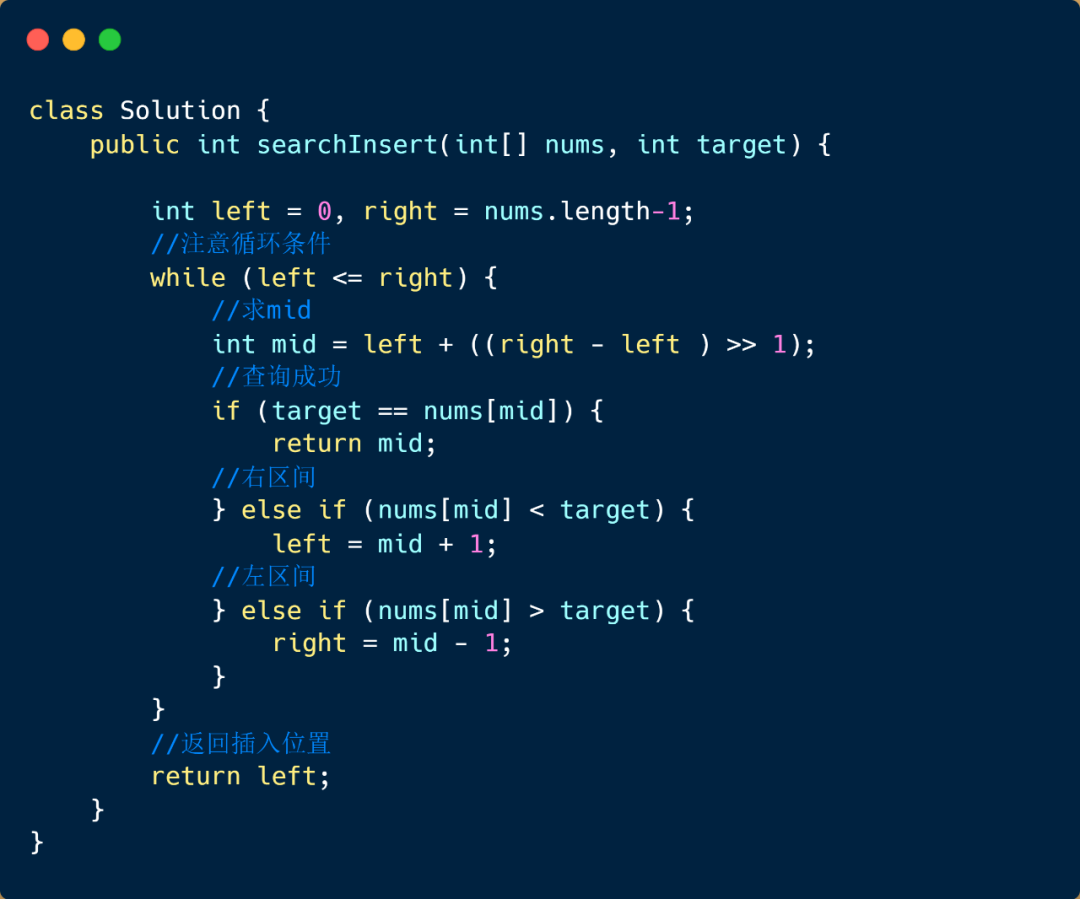
查找元素第一個位置和最后一個位置
上面我們說了如何使用二分查找在數組或區間里查出特定值的索引位置。但是我們剛才數組里面都沒有重復值,查到返回即可,那么我們思考一下下面這種情況
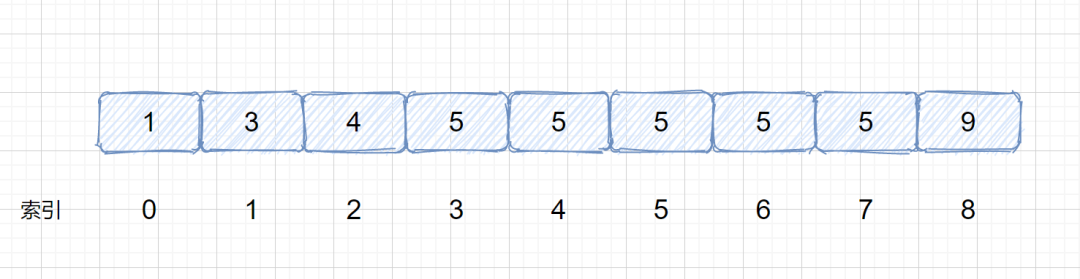
此時我們數組里含有多個 5 ,我們查詢是否含有 5 可以很容易查到,但是我們想獲取第一個 5 和 最后一個 5 的位置應該怎么實現呢?哦!我們可以使用遍歷,當查詢到第一個 5 時,我們設立一個指針進行定位,然后到達最后一個 5 時返回,這樣我們就能求的第一個和最后一個五了?因為我們這個文章的主題就是二分查找,我們可不可以用二分查找來實現呢?當然是可以的。
leetcode 34在排序數組中查找元素的第一個和最后一個位置
題目描述
給定一個按照升序排列的整數數組 nums,和一個目標值 target。找出給定目標值在數組中的開始位置和結束位置。
如果數組中不存在目標值 target,返回 [-1, -1]。
示例 1:
輸入:nums = [5,7,7,8,8,10], target = 8 輸出:[3,4]
示例 2:
輸入:nums = [5,7,7,8,8,10], target = 6 輸出:[-1,-1]
示例 3:
輸入:nums = [], target = 0 輸出:[-1,-1]
題目解析
這個題目很容易理解,我們在上面說了如何使用遍歷解決該題,但是這個題目的目的就是讓我們使用二分查找,我們來逐個分析,先找出目標元素的下邊界,那么我們如何找到目標元素的下邊界呢?
我們來重點分析一下剛才二分查找中的這段代碼

我們只需在這段代碼中修改即可,我們再來剖析一下這塊代碼,nums[mid] == target 時則返回,nums[mid] < target 時則移動左指針,在右區間進行查找, nums[mid] ?> target時則移動右指針,在左區間內進行查找。
那么我們思考一下,如果此時我們的 nums[mid] = target ,但是我們不能確定 mid 是否為該目標數的左邊界,所以此時我們不可以返回下標。例如下面這種情況。
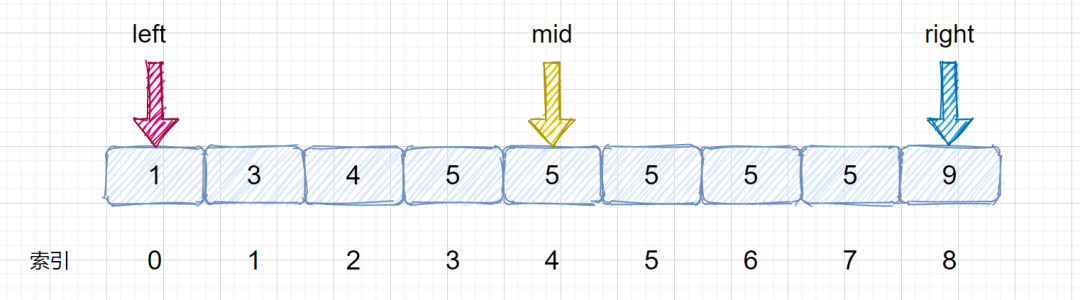
此時 mid = 4 ,nums[mid] = 5,但是此時的 mid 指向的并不是第一個 5,所以我們需要繼續查找 ,因為我們要找的是數的下邊界,所以我們需要在 mid 的值的左區間繼續尋找 5 ,那我們應該怎么做呢?
我們只需在target <= nums[mid]?時,讓 right = mid - 1即可,這樣我們就可以繼續在 mid 的左區間繼續找 5 。是不是聽著有點繞,我們通過下面這組圖進行描述。

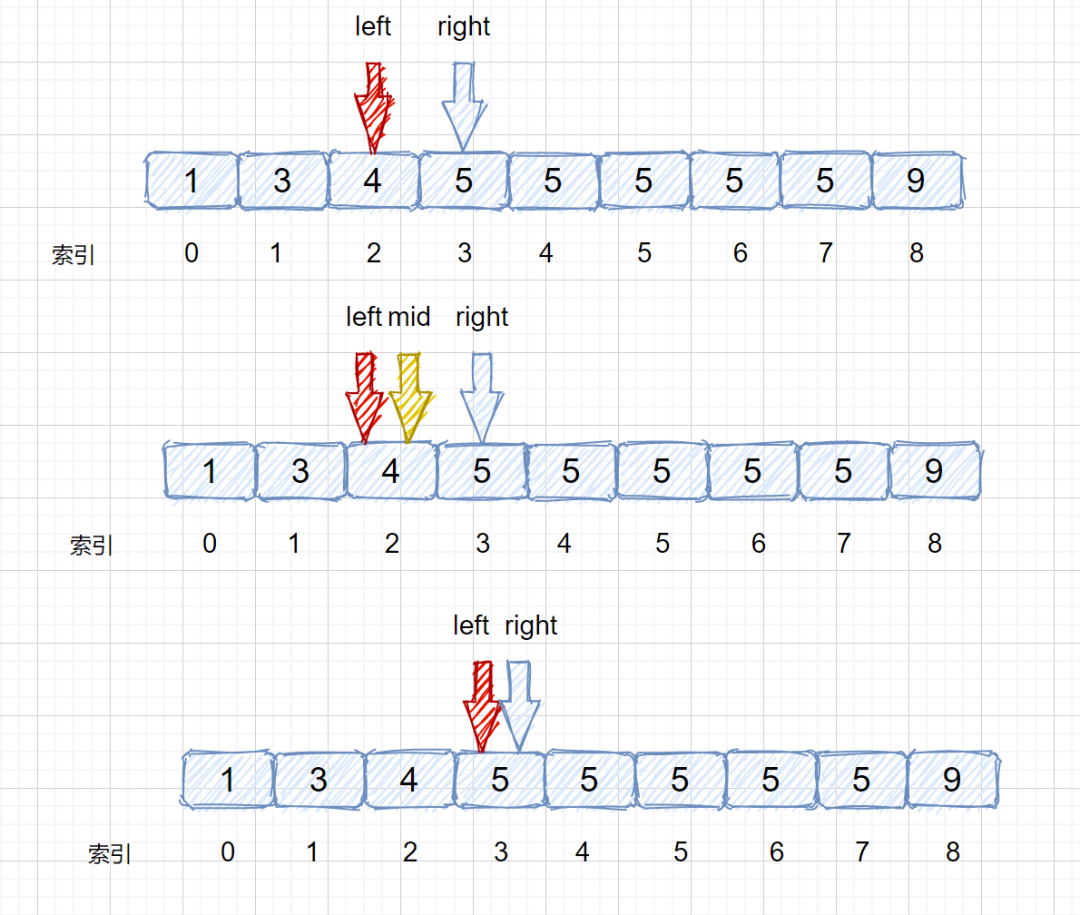
其實原理很簡單,就是我們將小于和等于合并在一起處理,當 target <= nums[mid] 時,我們都移動右指針,也就是 right ?= mid -1,還有一個需要注意的就是,我們計算下邊界時最后的返回值為 left ,當上圖結束循環時,left = 3,right = 2,返回 left 剛好時我們的下邊界。我們來看一下求下邊界的具體執行過程。
動圖解析
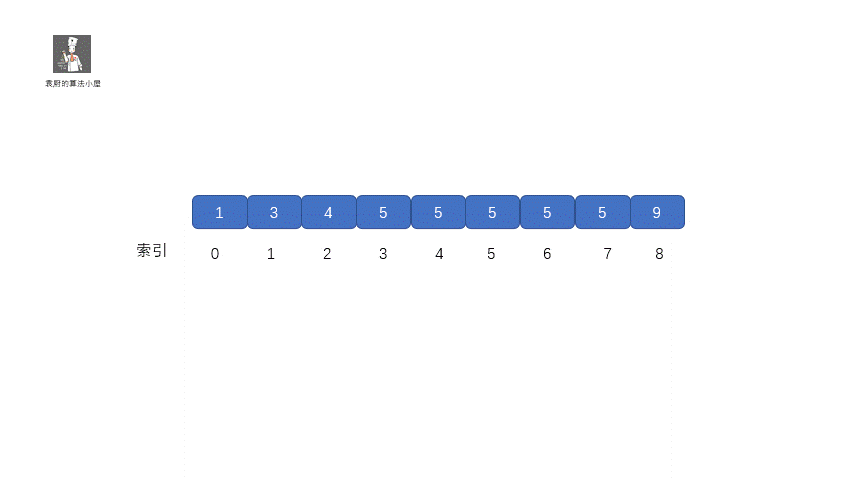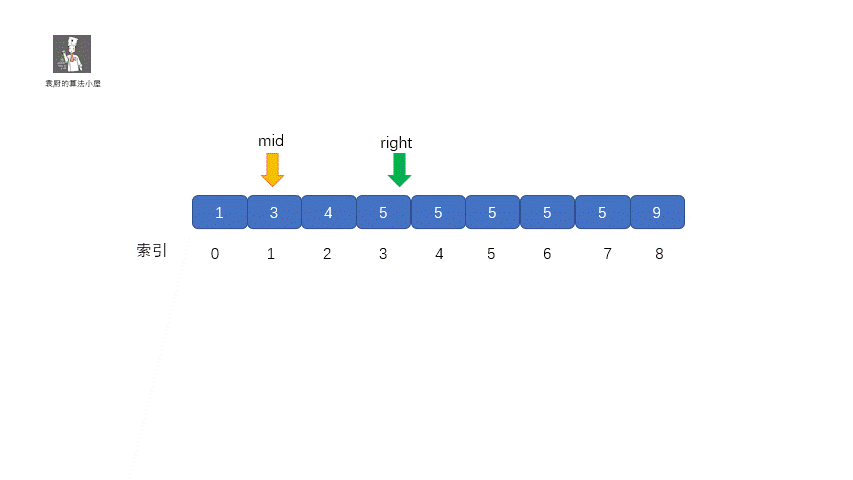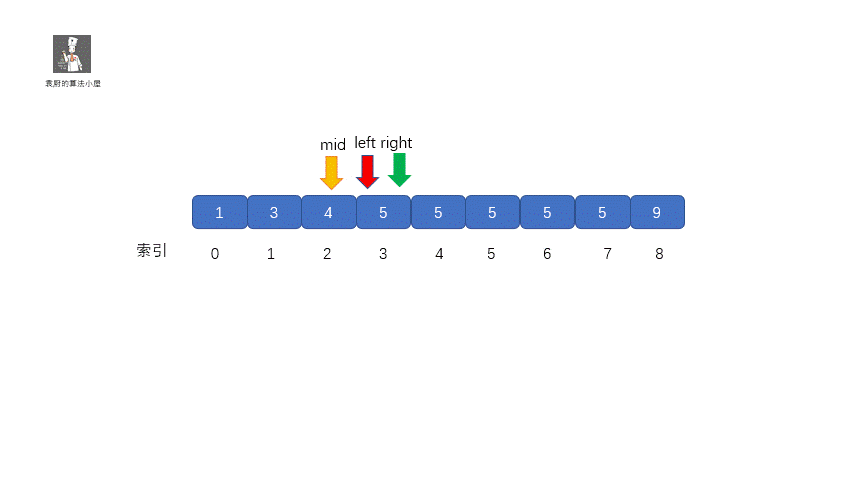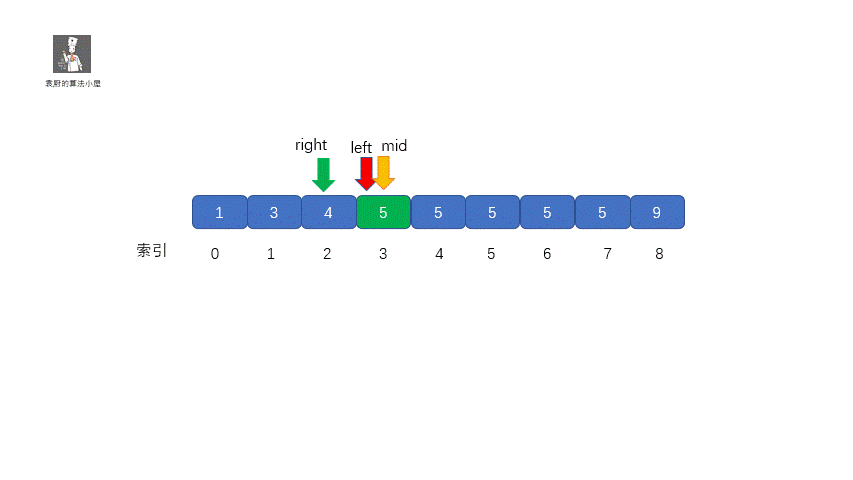
計算下邊界代碼
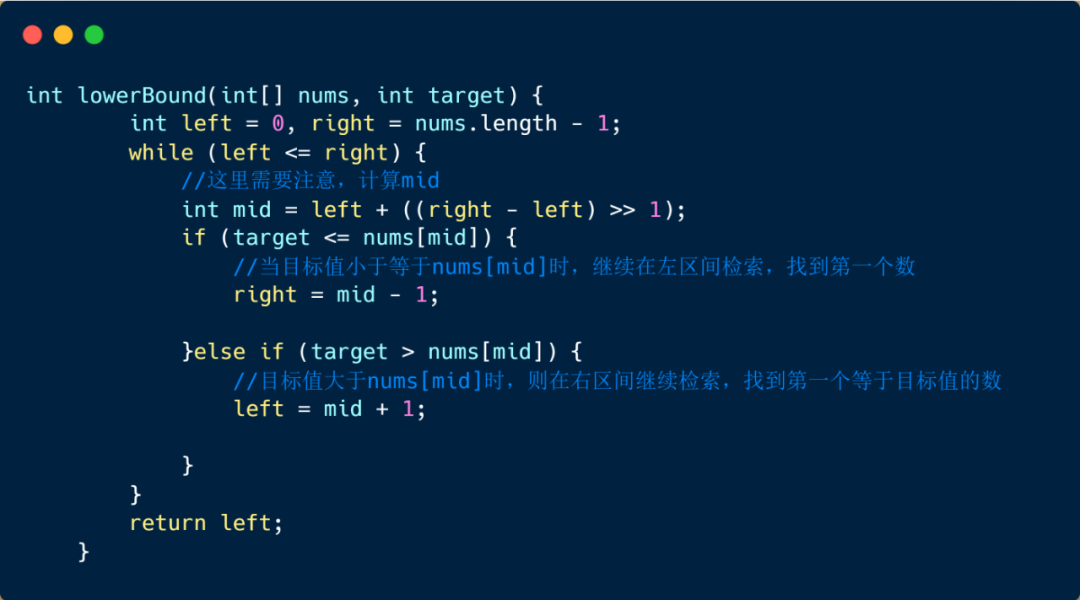
計算上邊界時算是和計算上邊界時條件相反,
計算下邊界時,當 target <= nums[mid] ?時,right = mid -1;target > nums[mid] 時,left = mid + 1;
計算上邊界時,當 target < nums[mid] 時,right = mid -1; target >= nums[mid] 時 left = mid + 1;剛好和計算下邊界時條件相反,返回right。
計算上邊界代碼
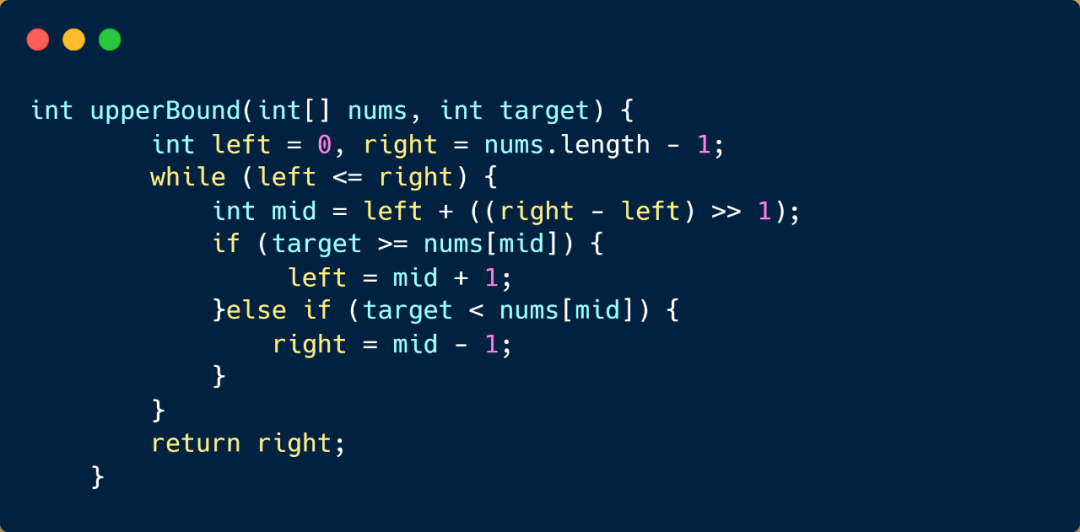
題目完整代碼
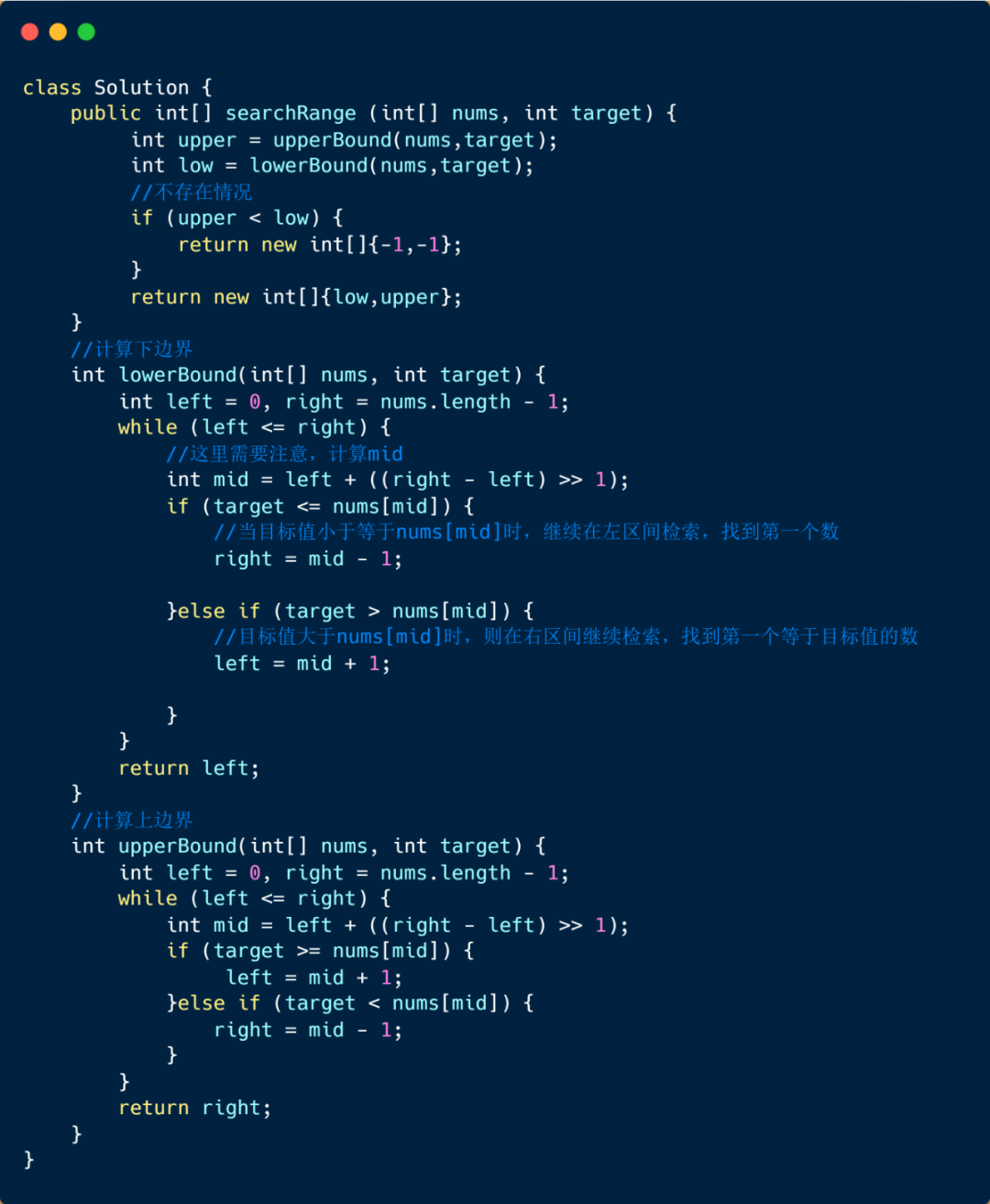
找出第一個大于目標元素的索引
我們在上面的變種中,描述了如何找出目標元素在數組中的上下邊界,然后我們下面來看一個新的變種,如何從數組或區間中找出第一個大于或最后一個小于目標元素的數的索引,例 nums = {1,3,5,5,6,6,8,9,11} 我們希望找出第一個大于 5的元素的索引,那我們需要返回 4 ,因為 5 的后面為 6,第一個 6 的索引為 4,如果希望找出最后一個小于 6 的元素,那我們則會返回 3 ,因為 6 的前面為 5 最后一個 5 的索引為 3。好啦題目我們已經了解,下面我們先來看一下如何在數組或區間中找出第一個大于目標元素的數吧。
找出第一個大于目標元素的數,大概有以下幾種情況
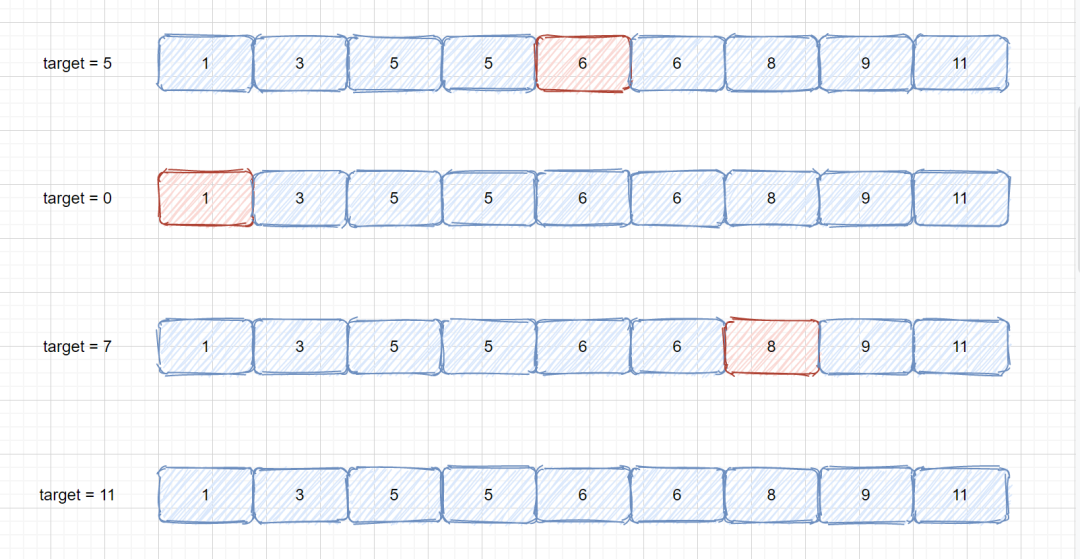
1.數組包含目標元素,找出在他后面的第一個元素
2.目標元素不在數組中,且數組中的所有元素都大于它,那么我們此時返回數組的第一個元素即可
3.目標元素不在數組中,數組內的部分元素大于它,此時我們需要返回第一個大于他的元素
4.目標元素不在數組中,且數組中的所有元素都小于它,那么我們此時沒有查詢到,返回 -1 即可。
既然我們已經分析完所有情況,那么這個題目對咱們就沒有難度了,下面我們描述一下案例的執行過程
nums = {1,3,5,5,6,6,8,9,11} target = 7
上面的例子中,我們需要找出第一個大于 7 的數,那么我們的程序是如何執行的呢?

上面的例子我們已經弄懂了,那么我們看一下,當 target = 0時,程序應該怎么執行呢?
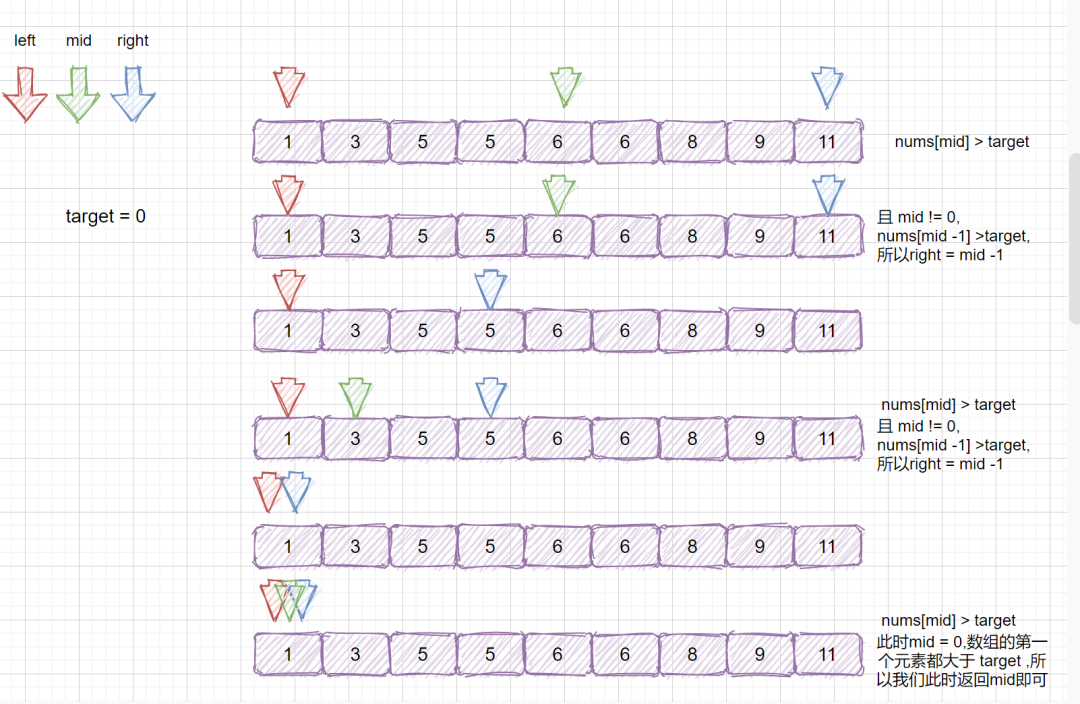
OK!我們到這一步就能把這個變種給整的明明白白的了,下面我們看一哈程序代碼吧,也是非常簡單的。

找出第一個小于目標元素的索引
通過上面的例子我們應該可以完全理解了那個變種,下面我們繼續來看以下這種情況,那就是如何找到最后一個小于目標數的元素。還是上面那個例子
nums = {1,3,5,5,6,6,8,9,11} target = 7
查找最后一個小于目標數的元素,比如我們的目標數為 7 ,此時他前面的數為 6,最后一個 6 的索引為 5,此時我們返回 5 即可,如果目標數元素為 12,那么我們最后一個元素為 11,仍小于目標數,那么我們此時返回 8,即可。這個變種其實算是上面變種的相反情況,上面的會了,這個也完全可以搞定了,下面我們看一下代碼吧。

不完全有序
查找目標元素(不含重復元素)
上面我們說二分查找需要在完全有序的數組里使用,那么不完全有序時可以使用二分查找嗎?我們一起往下看吧。
例:
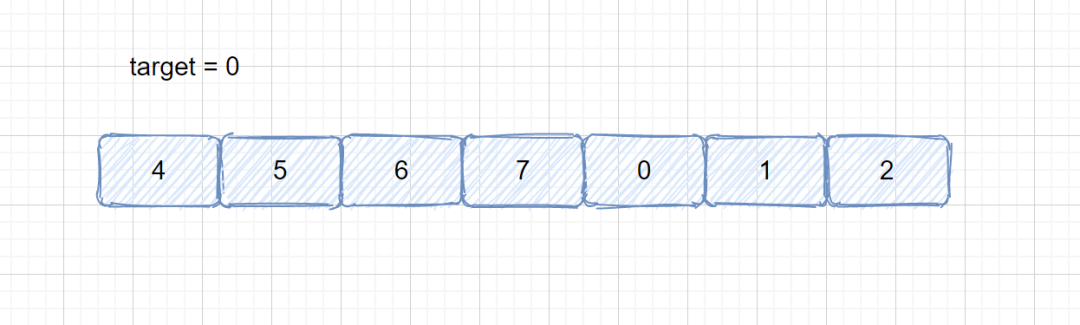
我們需要在上面的數組中查找我們的target,但是這個數組不是完全有序的應該怎么辦呢? 上面的新數組雖然不是完全有序,但是我們也可以找到規律,可以看成是由一個完全有序的數組旋轉得到的。或者可以理解成兩個有序數組,且第二個數組的最大值小于第一的最小值,我們將其拼接,拼接成了一個不完全有序的數組,在這個數組中我們需要找到 target ,找到后返回其索引,如果沒有找到則返回 -1;
下面我們看一下用二分查找解決該題的具體思路。 首先我們先設想一下mid值會落到哪里? 是不是只有兩種情況,和 left 在一個數組,同時落在數組1或同時在數組2,或者不在一個數組, left 在數組1,mid 在數組2。想到這里咱們這個題目已經完成一半了,見下圖。
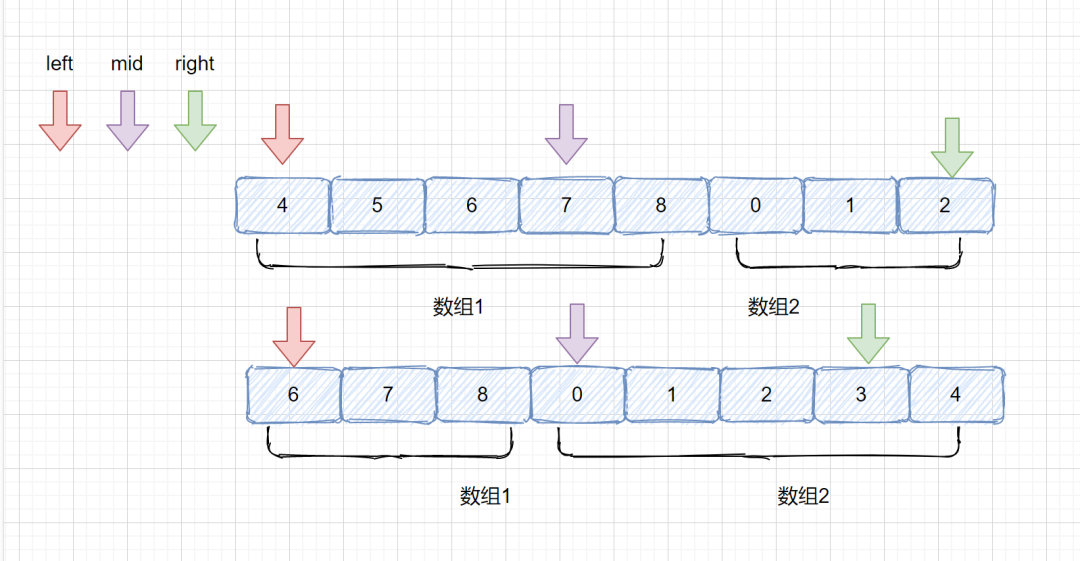
那么我們先來思考一下,我們怎么才能知道 left 和 mid 有沒有在一個數組里呢?
我們可以通過nums[mid] 和 nums[left] 比較進行判斷,因為我們的mid 一定是會落在 left 和 right 之間,那如果nums[mid] >= nums[left] 時,說明他倆落在一個數組里了,如果nums[mid] < nums[left]? 時,說明他倆落在了不同的數組,此時?left 在數組1 ,mid在數組2。
為什么我們可以通過這個進行判斷呢?我們想一下,如果left 和 mid 在 同一個數組里,且mid 一定在 left 的后面,在一個數組里,數組又是遞增的,那么nums[mid]> nums[left], 如果 nums[mid]< nums[left]?,且 mid 在 left 的后面,則說明 left 在數組1,mid 在數組2。
那么當left 和 mid 落在不同數組時,為什么不能是 left 在 數組2 ,mid 在 數組1 呢?
因為咱們的mid 是通過 left 和 right 的下標求得,所以mid 應該在 left 和 right 中間
如果我們的mid 和 left 在同一個數組內時?咱們的target會有幾種情況呢?
見下圖
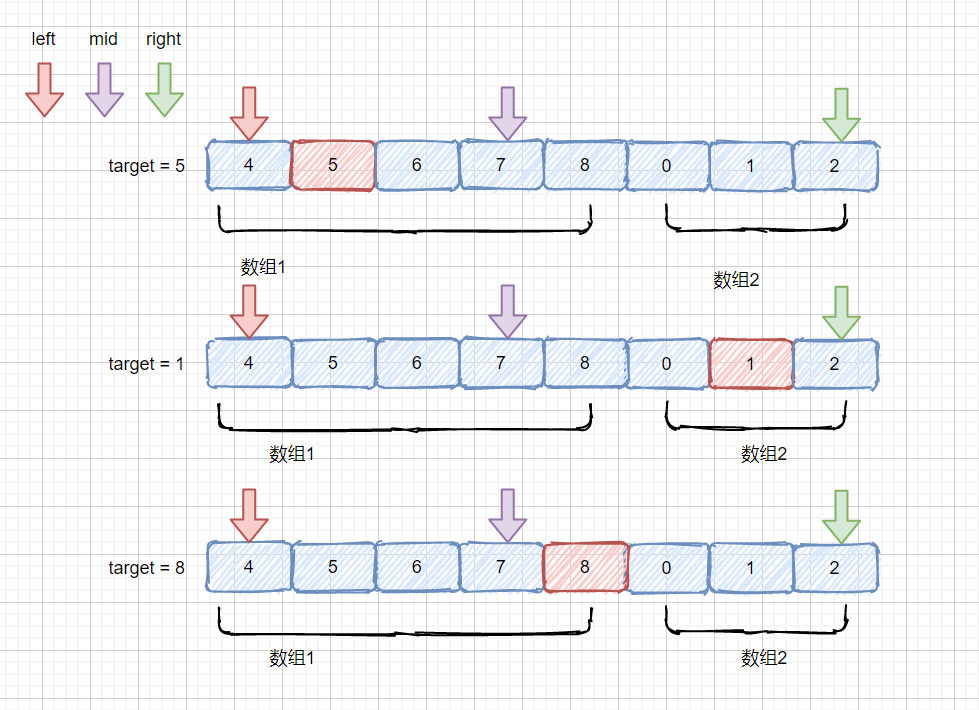
無非也是兩種情況,用我們上面的例子來說,
1.落在 mid 的左邊,target = 5,當前例子中 情況是落在[4,7)區間內,即 4 <= target < ?7 ,也就是??target ?>= nums[left] && target < nums[mid],此時我們讓??right = mid -1,讓 left 和 right 都落到數組 1 中,下次查找我們就是在數組1中進行了,完全有序,
2.落在 mid 的右邊,target = 1 ,target = 8 ,此時例子中 target 不落在 [4,7)區間內,那就target = 8或0 <= ?target <= 2(此時我們的 target 均小于 nums[left]) 兩種情況,也就是?target > nums[mid] || target < nums[left]??此時我們讓??left = mid + 1?即可,也是為了慢慢將left 和 right 指針趕到一個有序區間內。
那我們在來思考一下當 mid 值落在數組2中時,target 會有幾種情況呢?其實和上面的例子思路一致,情況相反而已。
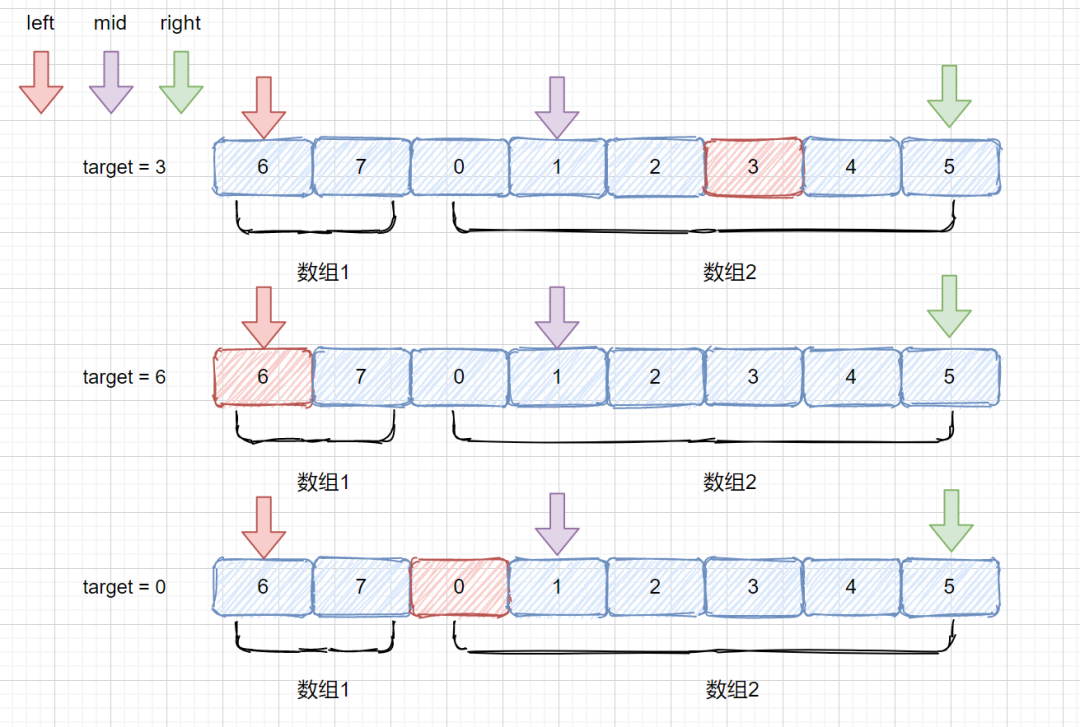
1. target <= nums[right] && target > nums[mid] 這里和上面的對應,此時的情況就是整個落在右半部分,我們下次就可以在數組2內進行查找。 2. target > nums[right] || target < nums[mid] 這里就是和上面的第二種情況對應,落在 mid 的左半部分,我們盡量將兩個指針趕到一個完全有序的區間內
通過上面的例子大家應該對該變種有所了解了,下面我們一起來做一下 leetcode 33 題吧。
leetcode33搜索旋轉排序數組
題目描述
給你一個整數數組 nums ,和一個整數 target 。
該整數數組原本是按升序排列,但輸入時在預先未知的某個點上進行了旋轉。(例如,數組 [0,1,2,4,5,6,7] 可能變為 [4,5,6,7,0,1,2] )。
請你在數組中搜索 target ,如果數組中存在這個目標值,則返回它的索引,否則返回 -1 。
示例 1:
輸入:nums = [4,5,6,7,0,1,2], target = 0 輸出:4
示例 2:
輸入:nums = [4,5,6,7,0,1,2], target = 3 輸出:-1
示例 3:
輸入:nums = [1], target = 0 輸出:-1
題目解析
這個題目的解答方法,咱們在上面已經有所描述,下面我們來看一下下面這個例子的代碼執行過程吧.大家可以結合代碼和動圖進行理解,代碼中所有語句都沒有進行簡寫,可以仔細閱讀判斷條件,很容易理解。
輸入 nums = [4,5,6,7,8,0,1,2] target = 8
動圖解析
下面我們看題目代碼吧,如果還沒有完全理解的同學,可以仔細閱讀 if ,else if 里面的語句,(沒有簡寫)還有文中注釋,一定可以整透的。
題目代碼

查找目標元素(含重復元素)我們通過剛才的例子了解了,如果在不完全有序的數組中查找目標元素,但是我們的不完全有序數組中是不包含重復元素的,那如果我們的數組中包含重復元素我們應該怎么做呢?見下圖
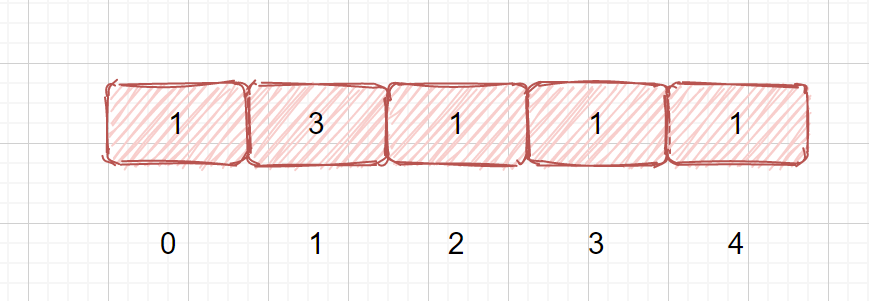
如上圖,如果我們繼續使用剛才的代碼,則會報錯這是為什么呢?我們來分析一下。
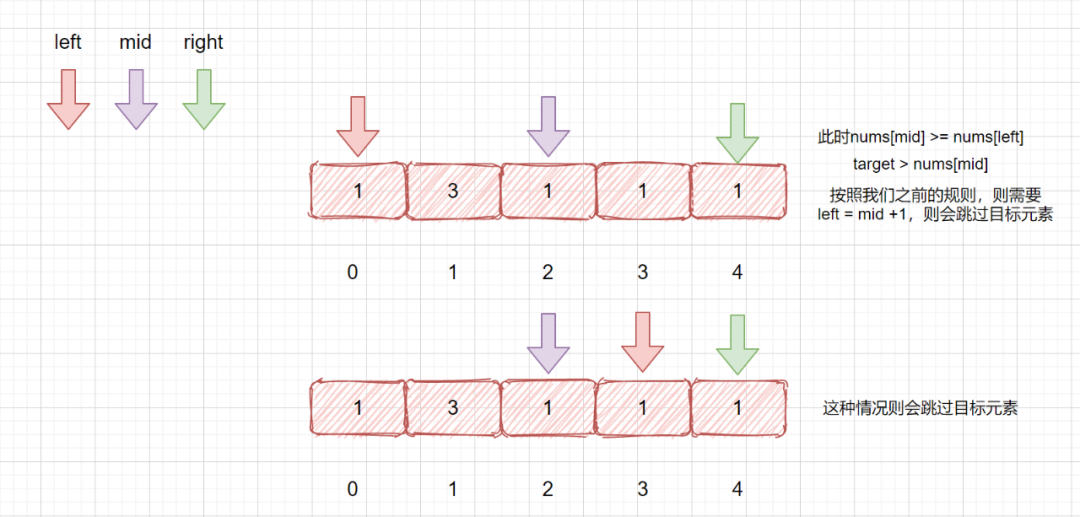
所以我們需要對其進行改進,我們只需將重復元素去掉即可,當我們的 nums[left] == nums[mid]時,讓 left ++ 即可,比如 1,3,1,1,1此時 nums[mid] == nums[left] 則 left ++,那我們此時會不會錯過目標值呢?其實并不會,只是去掉了某些重復元素,如果此時我們的目標元素是3,則我們left++,之后情況就變為了上題中的情況。 leetcode81. 搜索旋轉排序數組 II 題目描述
假設按照升序排序的數組在預先未知的某個點上進行了旋轉。
( 例如,數組 [0,0,1,2,2,5,6] 可能變為 [2,5,6,0,0,1,2] )。
編寫一個函數來判斷給定的目標值是否存在于數組中。若存在返回 true,否則返回 false。
示例 1:
輸入:nums = [2,5,6,0,0,1,2], target = 0 輸出:true
示例 2:
輸入:nums = [2,5,6,0,0,1,2], target = 3 輸出:false
題目解析這個題目就比剛才的不含重復元素的題目多了一個去除某些重復元素的情況,當 nums[mid] == nums[left]時,讓left++,并退出本次循環,其余部分完全相同,大家可以結合代碼和圖片進行理解。題目代碼
尋找最小值 這種情況也很容易處理,和咱們的leetcode33搜索旋轉排序數組,題目類似,只不過一個需要搜索目標元素,一個搜索最小值,我們搜索目標元素很容易處理,但是我們搜索最小值應該怎么整呢?見下圖
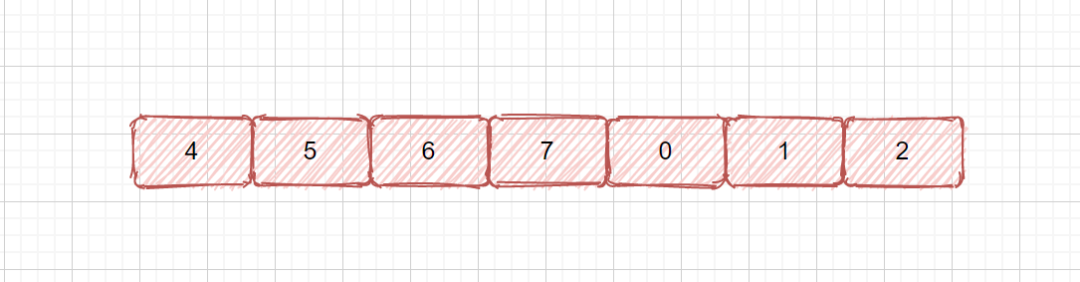
我們需要在一個旋轉數組中,查找其中的最小值,如果我們數組是完全有序的很容易,我們只需要返回第一個元素即可,但是此時我們是旋轉過的數組。 我們需要考慮以下情況
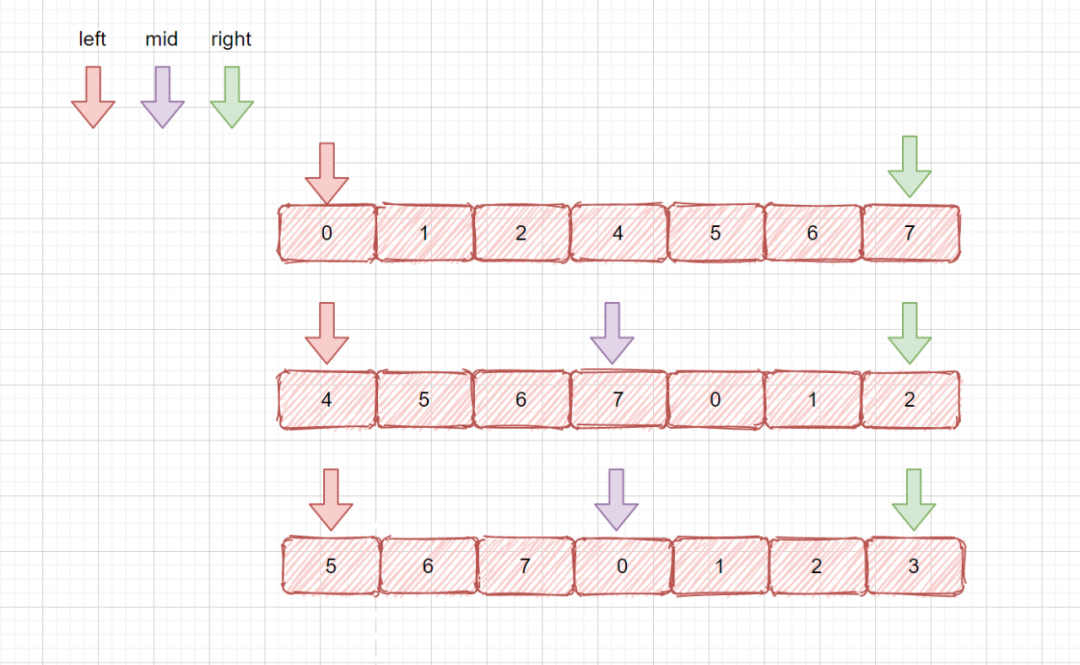
我們見上圖,我們需要考慮的情況是
數組完全有序nums[left] < nums[right],此時返回?nums[left]?即可
left 和 mid 在一個都在前半部分,單調遞增區間內,所以需要移動 left,繼續查找,left= mid + 1;
left 在前半部分,mid在后半部分,則最小值必在 left 和 mid 之間(見下圖)。則需要移動right ,right = mid,我們見上圖,如果我們 right = mid - 1,則會漏掉我們的最小值,因為此時 mid 指向的可能就是我們的最小值。所以應該是 right = mid 。
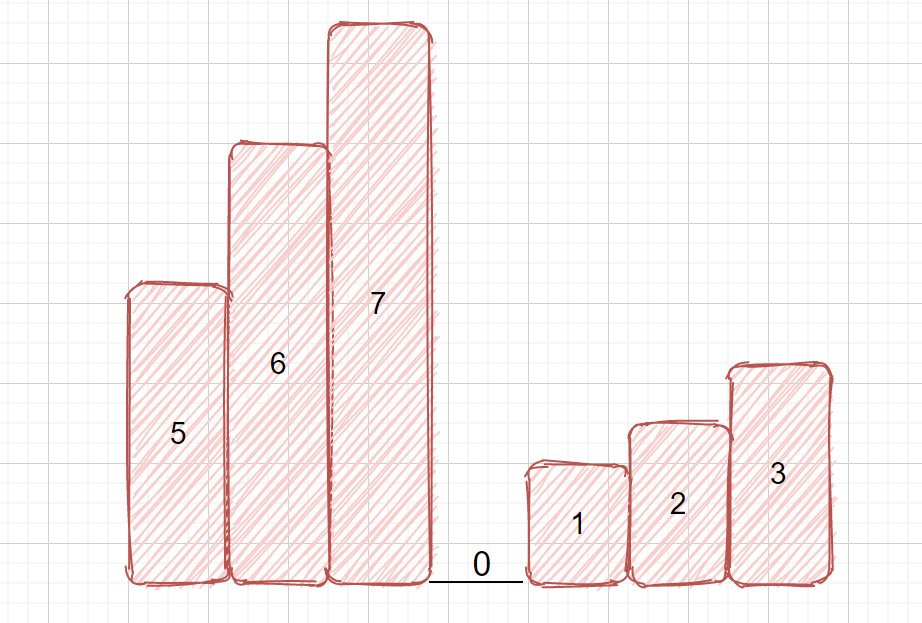
leetcode 153尋找旋轉數組中的最小值
題目描述
假設按照升序排序的數組在預先未知的某個點上進行了旋轉。例如,數組 [0,1,2,4,5,6,7] 可能變為 [4,5,6,7,0,1,2] 。
請找出其中最小的元素。
示例 1:
輸入:nums = [3,4,5,1,2]輸出:1
示例 2:
輸入:nums = [4,5,6,7,0,1,2]輸出:0
示例 3:
輸入:nums = [1]輸出:1
題目解析
我們在上面的描述中已經和大家分析過幾種情況,下面我們一起來看一下,[5,6,7,0,1,2,3]的執行過程,相信通過這個例子,大家就能把這個題目整透了。
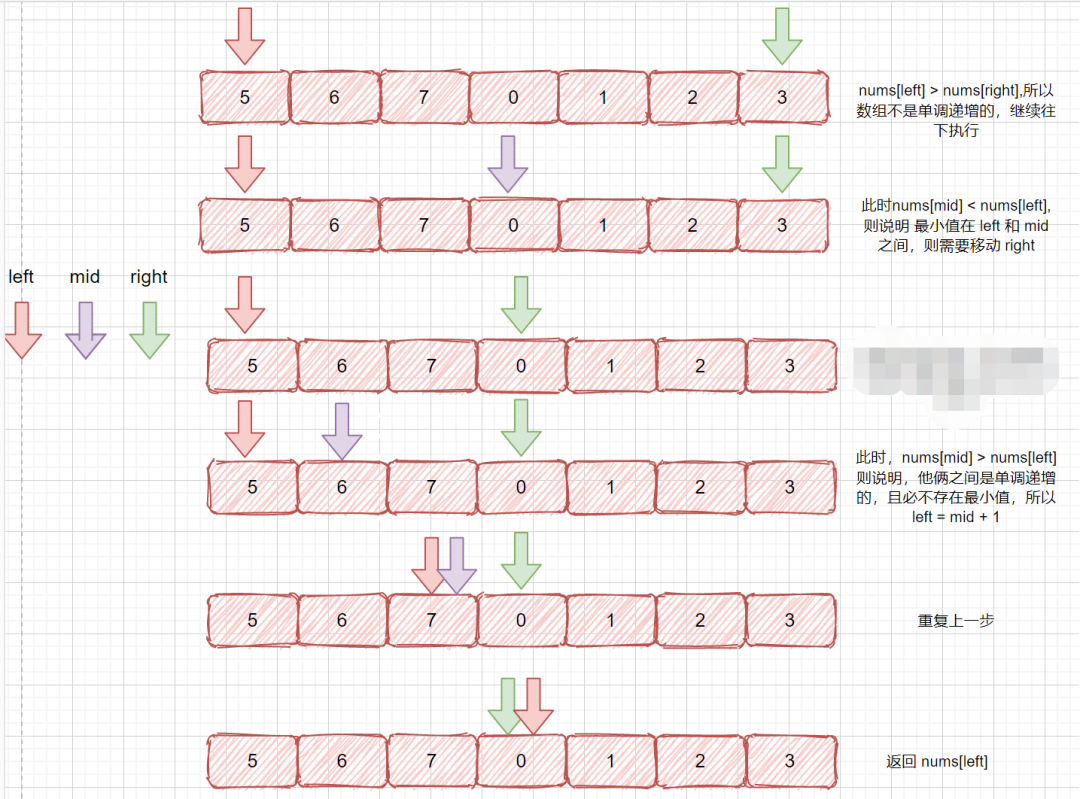
題目代碼

二維數組
查找目標元素
下面我們來看一下另外一種變體,如何在二維矩陣里使用二分查找呢?
其實這個很簡單,只要學會了二分查找,這個完全可以解決,我們先來看一個例子
我們需要從一個二維矩陣中,搜索是否含有元素 7,我們如何使用二分查找呢?
其實我們可以完全將二維矩陣想象成一個有序的一維數組,然后再用二分,比如我們的二維矩陣中,共有 9 個元素,那定義我們的left = 0,right = 9 - 1= 8,是不是和一維數組定義相同,然后我們求我們的 mid 值, mid = left +((right - left) >> 1)此時 mid = 4 ,但是我們的二維矩陣下標最大是,nums[2,2]呀,你這求了一個 4 ,讓我們怎么整呀。
如果我們理解了二分查找,那么這個題目考察我們的應該是如何將一維數組的下標,變為 二維坐標。其實也很簡單,咱們看哈,此時咱們的 mid = 4,咱們的二維矩陣共有 3行, 3列,那我們 mid =4,肯定在第二行,那么這個應該怎么求得呢?
我們可以直接用 (mid / 列數),即可,因為我們 mid = 4,4 /3 = 1,說明在第二行,那如果 mid = 7 ,7/3=2,在第三行,我們第幾行知道了,那么我們如何知道第幾列呢?我們可以直接根據 (mid % 列數 )來求得呀,比如我們此時 mid = 7,7%3 = 1,那么在我們一維數組索引為 7的元素(也就是10),其處于二維數組的第 3 行第 2 列,大家看看下圖是不是呀!
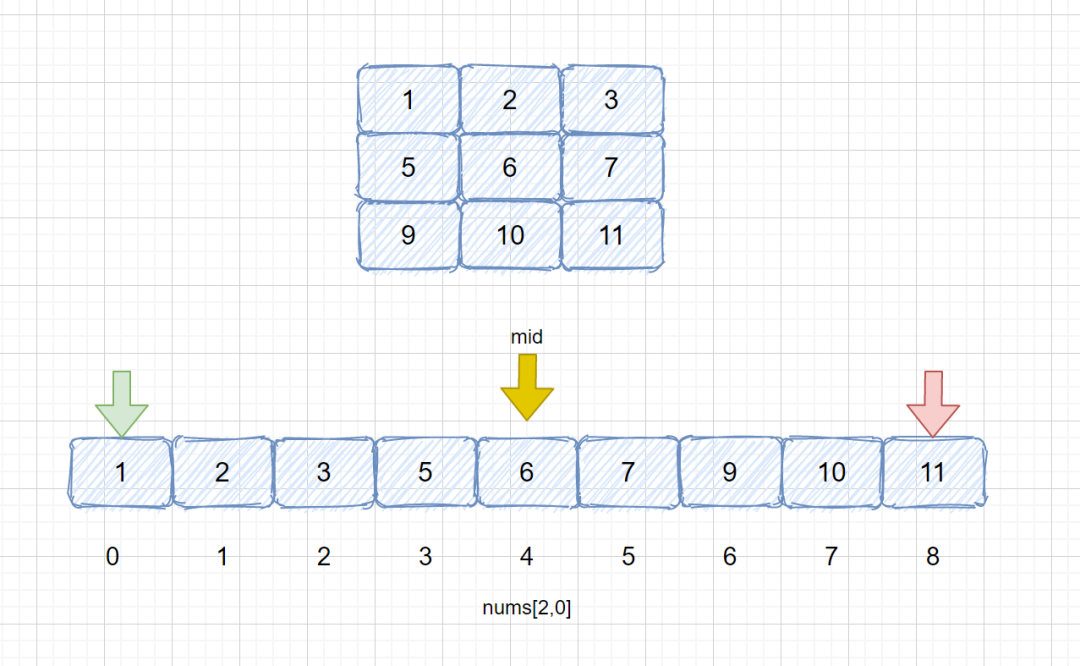
下面我們來看一下 leetcode 74題,讓我們給他整個通透
leetcode74搜索二維矩陣(中等)
題目描述
編寫一個高效的算法來判斷 m x n 矩陣中,是否存在一個目標值。該矩陣具有如下特性:
每行中的整數從左到右按升序排列。每行的第一個整數大于前一行的最后一個整數。
示例1
輸入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 3 輸出:true
示例2
輸入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 13 輸出:false
示例3
輸入:matrix = [], target = 0 輸出:false
題目解析
在上面我們已經解釋了如何在二維矩陣中進行搜索,這里我們再對其進行一個總結,就是我們憑空想象一個一維數組,這個數組是有二維數組一層一層拼接來的,也是完全有序,然后我們定義兩個指針一個指向一維數組頭部,一個指向尾部,我們求得 mid 值然后將 mid 變成二維坐標,然后和 target 進行比較,如果大于則移動 left ,如果小于則移動 right 。
動圖解析
題目代碼
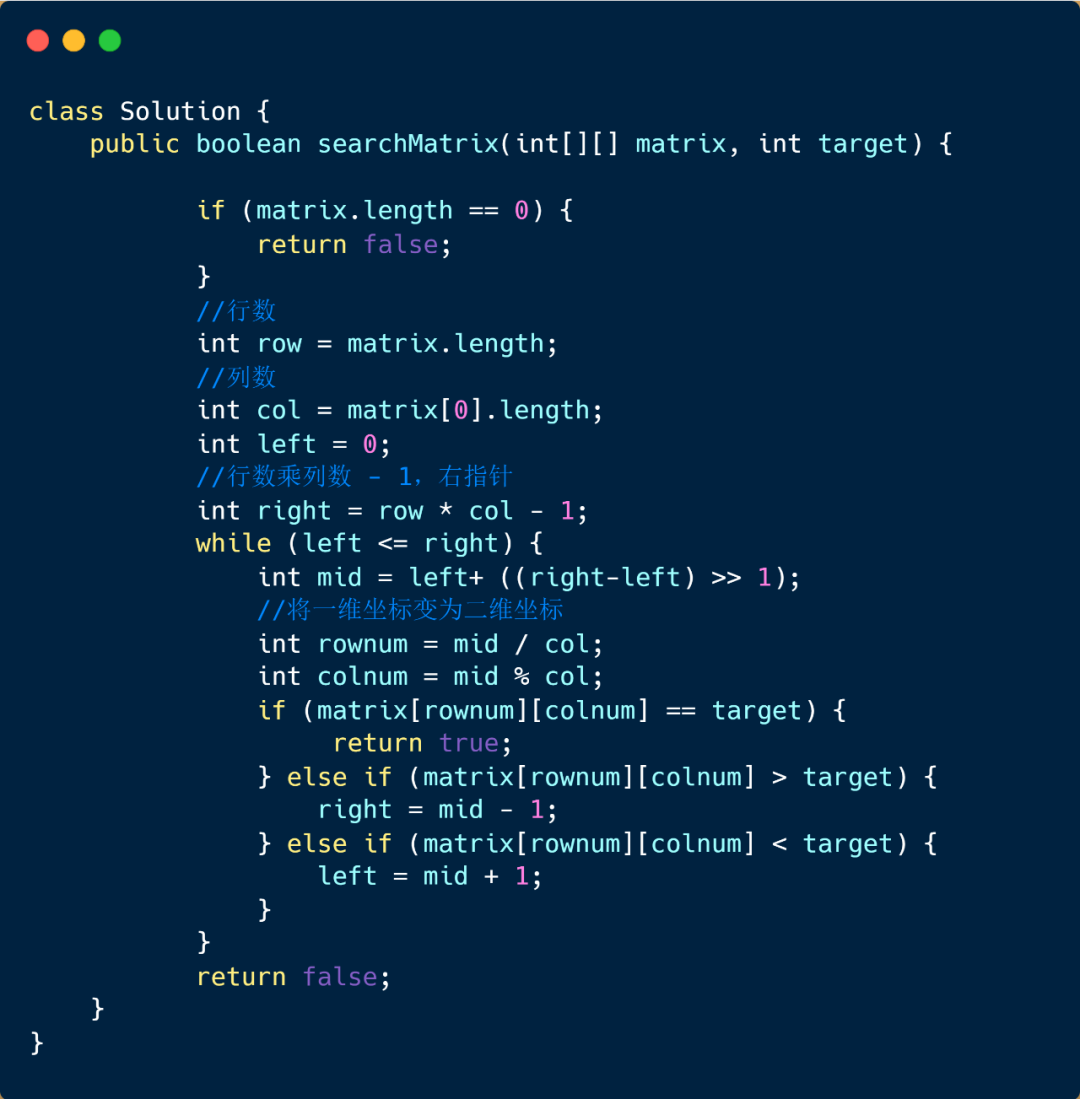
好啦 ,咱們的二分查找及其變種到這里就結束啦,希望通過這篇文章能讓大家掌握二分查找及其變種
責任編輯:xj
原文標題:穿了好幾個馬甲,差點沒認出來是二分查找
文章出處:【微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
-
查找
+關注
關注
0文章
5瀏覽量
8416 -
二分法
+關注
關注
0文章
5瀏覽量
7592
原文標題:穿了好幾個馬甲,差點沒認出來是二分查找
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
DAC3482設置DACCLK時,到底需要設置成和DATACLK相等還是二分之一的關系?
通過安卓手機查找IP地址步驟
Linux文件查找
直流接地故障的查找程序和方法
如何高效查找電氣故障
如何查找線路漏電的方法和步驟
功分器和耦合器的基本原理與應用
明治案例 | 【AI二分類】剝蒜機大蒜方向識別

二次回路多點接地故障查找儀裝置構成及原理——每日了解電力知識
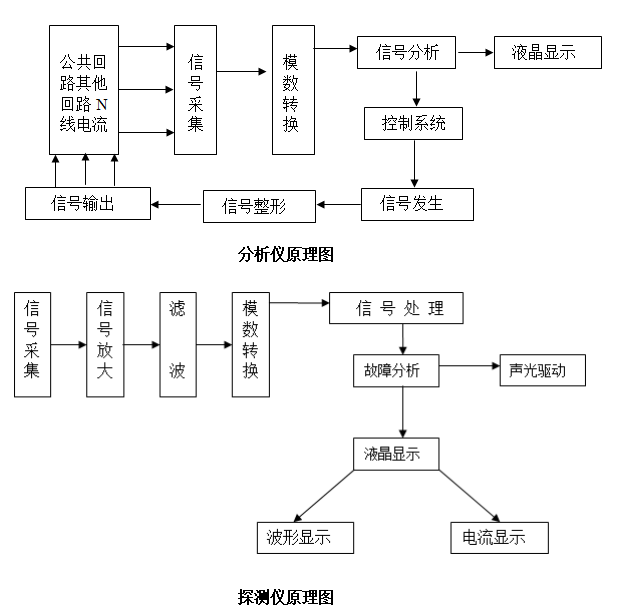
凱迪正大電纜故障查找定位:脈沖反射法的應用分享





 二分查找及其變種的總結
二分查找及其變種的總結











評論