1. 初相角
簡單交流發電機線圈轉到不同位置時,相對應電勢的正弦曲線圖。但以上討論,僅為選定參考時間起點時(即t=0)的情況。線圈平面(以α為參考)與發電機中心平面(以下簡稱線圈與x軸的夾角)之間的夾角為0°,如圖2-11(a)所示。因為在t=0時, et=0=0,而且當線圈反時針旋轉時,瞬時電勢e,是向正的方向增大。所以,得到電勢的正弦曲線,必然如圖2-11(b)所示。而其解析式即為
e=Emsinωt
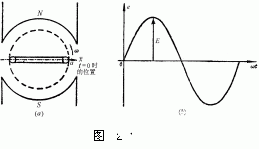
假定我們選定參考時間起點時(t=0),線圈與x軸的夾角為φ,如圖2-12(a)所示。
顯然,在t=0時,瞬時電勢e不等于零。而是:
et=0=Emsinφ。
在曲線圖上,在橫軸上t=0時,縱坐標為Emsinφ。當線圈反時針方向以ω角速度旋轉時,瞬時電勢逐漸增加。當轉過ωt弦度的角度時,如ωt+φ=90°,電勢達到最大值;再繼續旋轉,則電勢e將減小,如此該電勢的正弦曲線圖如圖2-12(b)所示。
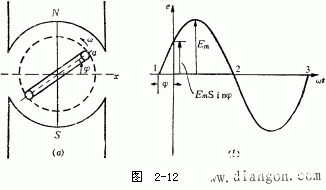
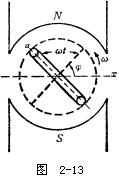
在t秒時,線圈位置如圖2-13所示。因此,瞬時電勢e的解析式為
e=Emsin(ωt+φ)。 (2-12)
式(2-12)是一般情形下的正弦電勢解析式;而式(2-7)是式(2-12)在φ=0°時的特殊情況。
φ角是在t=0時,決定瞬時電勢大小的一個定值(也就是選定參考時間t=0時,一對磁極的發電機線圈與x軸的空間夾角)。φ角稱為該正弦電勢的初相角(也叫初相位或初相)。顯然給定解析式,初相是很容易確定的。給定的正弦曲線上怎樣確定φ角呢? t=0(原點)及e=0點[從圖2-12(b)曲線圖可看出, e=0有1、 2、 3三點,這里應選1點,即選定e=0的點,必定符合隨著時間推移, e應該是向正值增加的點,這個角度才是對應圖2-12(a)發電機中線圈參考點α與x軸的夾角]兩點決定的長度在橫軸上按一定比例表示的角度,即為初相角φ。如: e=0點在原點左邊,則φ為正;如在右邊,則φ為負。圖2-12(b)的正弦曲線圖上的φ為正,而圖2-14(a)可看出,此時t=0,
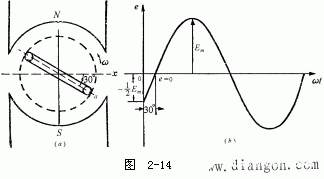
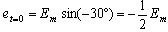
當隨著t的增加線圈轉過ωt=30°角度時,e=0。所以e=0的點在原點的右邊,初相角φ為負值。由此可畫出圖2-14(b)的正弦曲線圖,此時的解析式為e=Emsin(ωt-30°)。
應當指出,一般初相角φ在±180°以內。
〔例2-4〕已知正弦電勢曲線圖如圖2-15(b)所示。
試畫出一對磁極發電機線圈位置,列出解析式,并求初相角。

[解]∵ e=0及t=0, 1—2之間弧度為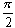 ∴ 初相角φ=90°
∴ 初相角φ=90°
線圈位置參考點α與x夾角為+90°,如圖2-15(a)所示,其解析式:
e=Emsin(ωt+90°)
[解]顯然φ=-120°,則線圈參考點α與x軸夾角應為順時針120°,當線圈轉30°后,電勢e為負的最大值,再轉90°時為e=0處,所以可得線圈位置及曲線圖如圖2-16(a)、 (b)所示。
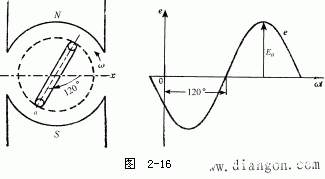
由上面的分析可知,只要一個正弦量的極大值,頻率(或T、 ω)以及初相角已知,則該正弦量就確定了,因此我們把決定正弦交流電的這三個特征量,稱為正弦交流電的三要素。
2. 相位差
在交流電路中,有時往往要比較兩個相同頻率的正弦量,除了比較它們的極大值的關系外,還要比較它們的相位關系。
如有兩個相同頻率的正弦量
e1=Em1sin(ωt+φ1)
e2=Em2sin(ωt+φ2)
這兩個相同頻率交流電初相之差稱為相位差,用φ12表示。即: φ12=φ1-φ2。
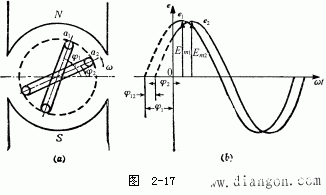
設在一個發電機中,繞有兩個獨立的線圈1及2,如圖2-17(a)所示。其正弦電勢曲線如圖2-17(b)所示。顯然從發電機線圈位置并結合曲線可以看出, e1比e2早到達極大值,因此可叫做e1超前e2(超前φ1-φ2角)或叫做e2滯后e1(滯后φ1-φ2角)。這里應當注意的是,超前或滯后一般規定不得大于180°。如果兩者初相相同,叫做同相。如果兩者相位相反(即相位差為180°),則叫做反相。在比較一個交流電路中幾個正弦交流電時,除了頻率和極大值外,往往關心的是它們的相位差,所以常選擇電路中某一正弦量的初相為0°(這樣最簡單),這個正弦量稱為參考正弦量。
〔例2-6〕已知兩正弦電勢解析式如下:
e1=100sin(ωt+120°),
e2=50sin(ωt-30°)。
試畫出一對磁極發電機電樞線圈位置及其曲線圖,求出每一電勢的初相及其相位差,并指出哪個超前,超前多少?
[解]線圈位置及曲線如圖2-18(a)、 (b)所示。
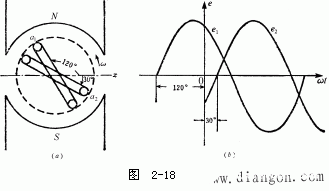
e1的初相角為120°,
e2的初相角為-30°,
φ12=φ1-φ2=120°-(-30°)=150°,
e1超前于e2150°。
責任編輯:lq
-
線圈
+關注
關注
14文章
1838瀏覽量
44580 -
交流電
+關注
關注
14文章
672瀏覽量
34068 -
電勢
+關注
關注
0文章
74瀏覽量
13667
發布評論請先 登錄
相關推薦
電路小知識 | 交流電路復數的基礎知識以及相位差和電抗的計算
兩個高速ADC的CLK時鐘如何做到同步無相位差?
【電路小知識】深入解析交流電路基礎:波形與特性詳解
一文弄懂實時動態載波相位差分技術和偽距差分技術的區別

需要對兩個信號(10M的信號)進行去相位差的運算,如何消除或者補償電路對兩信號相位差的改變?
使用泰克示波器觀察相位差

使用LM358設計了一個差動放大電路,為何無法產生10V的交流電呢?
電容電壓電流相位超前與滯后判斷
交流電經過電容后電流相位如何改變
影響感性負載電流與電壓相位關系的因素
示波器測量相位差的原理和方法簡析
普源示波器測量相位差的原理和方法




 交流電的初相角和相位差
交流電的初相角和相位差










評論