很少有在壓控音頻濾波器拓撲結構使用的濾波器。這引起了我對這種電路的興趣。壓控濾波器(VCF)在音頻電路中是一個有用的,甚至是必不可少的元件。憑借20世紀模擬工程師的所有創(chuàng)造力,這些電路稀缺的事實令人著迷。為什么拓撲結構這么少?為什么現(xiàn)有的拓撲結構看起來都不像濾波器?
用于音頻應用的壓控濾波器
壓控濾波器(VCF)是模擬合成器的支柱。最常見的配置是使用基于運算跨導放大器(OTA)的濾波器,LM13600和LM3080等集成電路是受歡迎的選擇。Korg根據(jù)Sallen-Key或OTA制造了諸如Korg35、4023、4025和4075等芯片。但是有一個濾波器比其他濾波器更出色,因為它具有創(chuàng)造性、有效性,而且(很好的權威性)可以聽到出色的聲音。這是Moog階梯濾波器。
Moog梯形濾波器原理圖
下面來看看Moog濾波器。
圖1.MoogProdigy模擬合成器中出現(xiàn)的著名Moog濾波器。
在這里看到八個晶體管在一個階梯中,有一個電阻分壓器鏈,由一個偏壓/控制電流Ibias驅(qū)動。音頻輸入應用于Q1,反饋(用于共振,在電子音樂中也稱為強調(diào))應用于Q2,而其他晶體管成對,連接在基極,電容器并聯(lián)其發(fā)射器。作為最頂部電容兩端的電壓輸出。為了簡化這一點,我們可以(小心)去掉偏置組件,得到如圖2所示的原理圖。
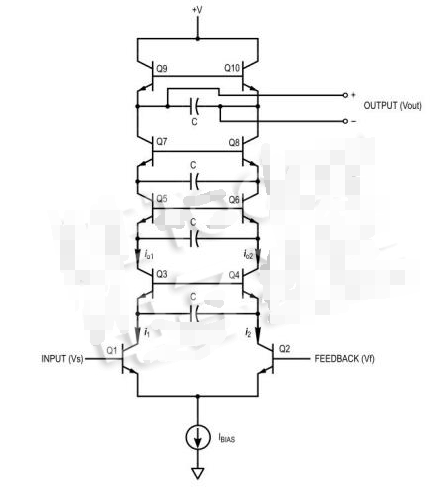
圖2.Moog濾波器的簡化原理圖
這只是有點誤導,因為基地不是浮動的,而是通過一個除法器保持恒定的電位。
Moog梯形濾波器解釋
來看看電路。電路的截止頻率控制是施加到差分對Q1-Q2的電流Ibias。對于整個網(wǎng)絡,改變Ibiass會導致晶體管的偏置電流發(fā)生變化。忽略基極電流(即假設高β)我們看到流過Q1的直流電流必須流過左側階梯的其余部分,同樣,對于Q2和右側階梯的直流電流也必須流過。
晶體管對Q3-Q4、Q5-Q6和Q7-Q8均具有兩個晶體管和一個電容器。成對的晶體管共享相同的基極電壓但具有不同的發(fā)射極電流。由于小信號電流是不同的,用于晶體管的小信號Vbe將是不同的,因此在發(fā)射極電容器之間會產(chǎn)生電位。電容器是頻率相關的電抗,產(chǎn)生濾波效應。為了了解這有多精確,必須分析濾波器的三個不同部分,如圖3所示。
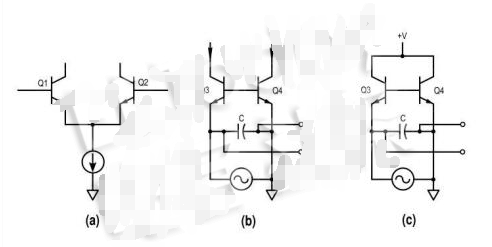
圖3.梯形濾波器拓撲的三個元素(a)驅(qū)動差分對(b)中間階梯低通濾波器部分(c)最頂部的輸出濾波器部
該電路可分為驅(qū)動器(圖3a)和低通濾波器(圖3b和3c)。(b)和(c)的輸入源是電流信號,在反饋側接地以便于分析(通過對稱確認這是安全的)。
驅(qū)動

圖4.濾波器的驅(qū)動部分。
驅(qū)動部分是差分對,也稱為發(fā)射極耦合對。為了從小信號的角度分析該電路,我們可以用適當?shù)囊纛l有源區(qū)模型替換晶體管。兩種常見的選擇是混合π模型(以輸入電阻建模的跨導)或T模型(以基極發(fā)射極電阻建模的跨導)。
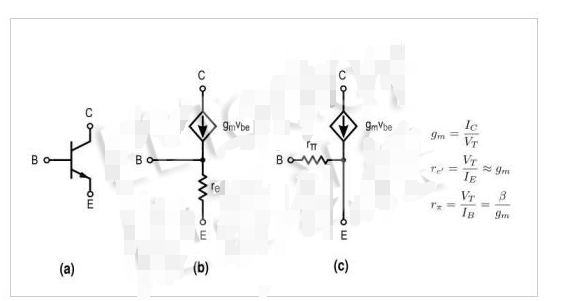
圖5.三種晶體管模型(a)NPN晶體管(b)T模型(c)混合π模型
T模型和混合π模型中的電阻與等于晶體管β的因子相關。雖然它們具有不同的電路配置,但模型在分析上是相同的。對于驅(qū)動電路,我們可以使用混合π模型。
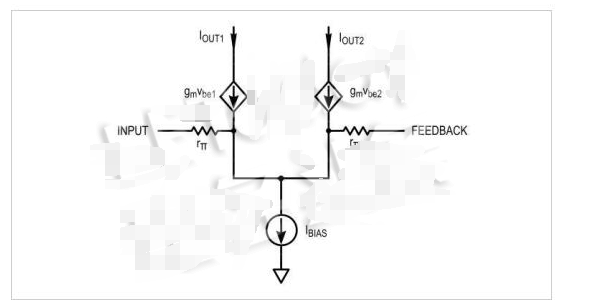
圖6.用晶體管的低頻混合π等效模擬驅(qū)動器中的晶體管。
用開路代替恒流源,用接地代替恒壓源,可以簡化電路,如圖7所示。對于小信號電流增益計算、負載短路,使我們能夠有效地將集電器接地。通常,我們也會計算輸出阻抗來計算負載,但在這種情況下,我們不必這樣做。這可以通過依賴電流源的存在來證明,并且因為沒有考慮厄利效應(其表現(xiàn)為與電流源并聯(lián)的輸出阻抗)。我們不會考慮共模效應,因為晶體管的偏置點足夠小。最后,為了模擬差分輸入,我們將向兩個晶體管施加相等和相反的輸入電壓。這不是絕對必要的,但它會使分析更容易。
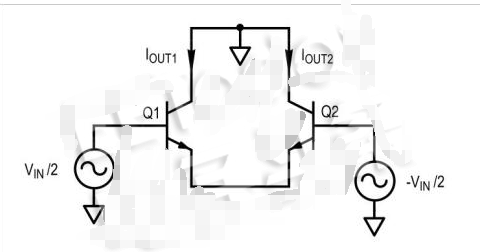
圖7.使用一些簡化技術進行分析的小信號電路。
責任編輯人:CC
-
濾波器
+關注
關注
161文章
7859瀏覽量
178694 -
壓控濾波器
+關注
關注
0文章
3瀏覽量
6560
發(fā)布評論請先 登錄
相關推薦
使用數(shù)字濾波器塊怎么實現(xiàn)梯形濾波器
電源濾波器的作用和特點,電源濾波器電路圖解析
詳細解析濾波器的定義,濾波器的特性,濾波器的工作原理,濾波器的分類,濾波器的典型電路原理圖

LTCC低通濾波器的設計解析
模擬電源和數(shù)字電源的原理圖解析
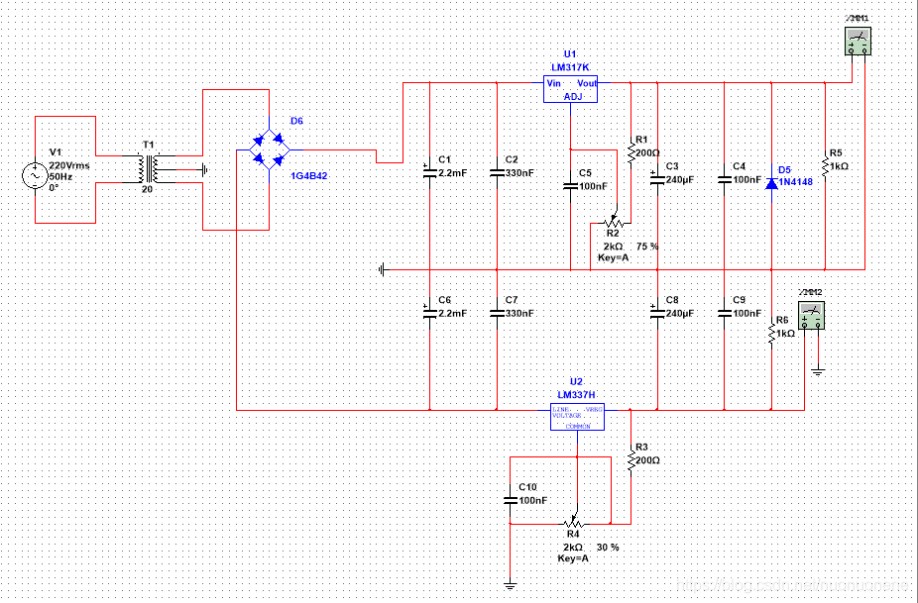
電壓和電流對電源濾波器的影響及損壞原因解析





 Moog梯形濾波器原理圖解析
Moog梯形濾波器原理圖解析














評論