1 引言
EDFA模塊主要包括兩部分:光路模塊和電路模塊。光路模塊的功能是光信號的驅動放大,電路模塊則用于對光路模塊中泵源980nm激光器進行測控,使EDFA整機按預定預置的各項指標長期穩定、可靠的工作。本文設計了一種高精度、寬范圍的溫控電路。
2 980nmLD組件特性
2.1 980nmLD組件
980nmLD載體器件安裝在半導體制冷器上,通過改變流過制冷器的電流方向(決定致冷或加熱)和大小,調節載體的溫度。載體上安裝有熱敏電阻 RT為溫度傳感器。
2.2 980nmLD的熱傳導模型
若流入(出)載體的熱量速率為q , 載體向周圍散發(吸收)的熱量速率為qs ,根據熱力學定律有如下關系:
Cdθ/dt=q-qs (1)
式中,C是載體的熱容量。載體溫度 θ的大小決定于i流過半導體制冷器產生的電功率。因而 q與i為函數關系,且為非線性關系:q = f (i)。 由于最關心的是穩定值(亦工作點Θ 0 ,I0)附近的變化。為此,將函數 q = f (i)進行線性化處理;并考慮到:
qs=θ/R (2)
R是載體向周圍傳熱的熱阻;并令: CR=T0,T0是 θ(t)變化的時間常數;kR=K 0,
![]()
則式(1)可寫成動態方程:
![]()
這就是流過半導體制冷器的電流I (t)與載體溫度q(t)的動態微分方程。若 i(t)象函數為I(s);q (t)的象函數為Q(s),則式(4)可寫成傳遞函數形式:
![]()
顯然,這是一個慣性環節。
設熱敏電阻RT的熱容量為 CT,載體向熱敏電阻輸出熱量的速率為 qT,熱阻為RW。在載體溫度 θ的作用下,RT的溫度θ T由以下方程描述:

用傳遞函數表示:θ(t) 象函數為Θ(s): θT(t)象函數為Θ T(s)則
![]()
其中,TW=C TRW,這是積分環節。
3 用于溫度穩定的(模擬)自調系統
為了使980nmLD穩定在預置(或給定)的溫度上,溫控系統應設計成自調系統。該系統的調節對象是“制冷器”,輸出量是載體溫度 θ(t),象函數是Θ(s);輸入量,亦給定值以電壓形式 uD(t)輸入,其象函數為U D(t),則自調節系統方框圖如圖1所示。以下給出組成方框圖各部分的硬件電路,然后對系統的品質和誤差進行分析和檢測。
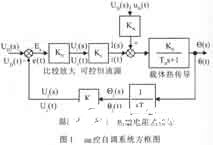
3.1 可控恒流源
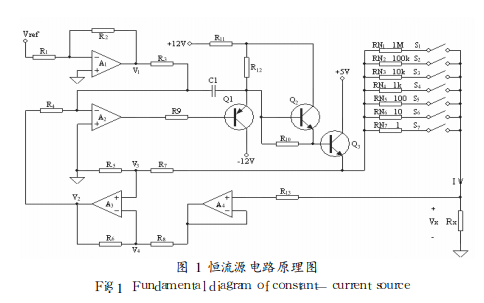
在圖1溫控系統中,可控恒流源實質上是執行機構。圖2(a)是可控恒流源電原理圖。圖中:IC1是電流取樣負反饋放大器;IC2是誤差放大器,;T1 、T2構成電流放大器。
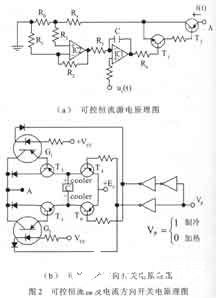
圖2(a)是由電流負反饋電路構成的恒流源。輸出恒流i(t)流入制冷器。經推導i (t)與輸入(控制)電壓ui( t)有如下關系:
顯然KI為常數。這就是說,恒流源的輸出與運放及晶體管參數無關,只與電阻R1、 R2和R0有關。因此,本恒流有很高的穩定性。圖2(b)中,由T3~T6構成橋開關。由數字開關信號 Vp(TTL電平)控制恒流源輸出電流的方向。
3.2 溫度測量反饋電路
由于載體溫度與熱敏電阻R T的阻值為單值單調對應關系。因此,通過檢測裝在載體中的熱敏電阻 RT的阻值來確定載體溫度。圖3是常用的溫度-電壓變換電橋電路。
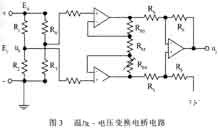
由圖可知,電橋輸出(uT -u0),再經放大得:

若對應溫度q1 、q2、q3的輸出定為 u01、 u02 u03,則線性化的條件是u 02=(u03-u01 )/2。為簡化,令u01=0,u 02= u03/2,根據R1和 q的對應關系,可選q1=0℃,q 2=25℃,q3=50℃,對應的電阻為: R T1,R T2和R T3,滿足三點線性化的方程組:

解方程得:
![]()
將R T1、R T2、RT3代入上式得:R 0=7.837kΩ,并計算出θj- uj曲線,如圖4所示,該曲線在0℃、25℃和50℃三點滿足線性化條件,曲線近似成直線,則 Ui(t)=K jqj(t) (8)
Kj為直線斜率,計算得 Kj=94.387mV/℃。

3.3 系統品質分析
由圖1,可得輸入為給定量象函數U D(s),輸出為溫度象函數Θ(s ),溫度自調節系統的傳遞函數:
![]()
當給定值不變,或UD (s)=0,擾動電壓UN(s ),溫度變化ΘN(s),方框圖如圖5所示。
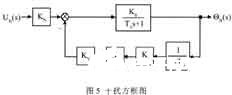
由圖5可得在UN( s)作用下的擾動傳遞函數:
由圖1,當UN(s )=0狀態下,得出誤差信號e(t)的象函數 E(s):
由式(9)~(11),對系統品質如下分析。 (1)無靜差系統
若擾動信號uN( t)=1(t),擾動靜差qN (t)可根據終值定理求得:
其中:UN(s )=1/s,引入式 (10),則:
![]()
為無擾動靜差。由式 (11),不難求得給定靜差。令UD(s )=1/s,則給定靜差:
e(t)|=limsxE(s)=0
(2)最佳狀態
由式(9)可寫出系統的特征方程:
T0s2 +s+KVKI K0Kj/T W =0 (12)
首先判斷系統是否穩定。由式(12)可知,方程的各階系數均大于零,且不缺項,根據代數法穩定判據,系統穩定。
再根據方程的根:
![]()
因圖1中的比較放大器KV 是比例放大器(電路圖略),改變放大器的比例電阻,亦可改變 KV。改變KV可使系統出現三種狀態:欠阻尼狀態、過阻尼狀態、臨界狀態,若使4KVK IK0KjT 0/TW 在0附近,則系統進入臨界狀態,此時上升時間短而又不振蕩,為最佳狀態。實驗表明此時 KV為40~50。
3.4 系統誤差分析
上述自調系統的溫控精度實測結果是:窄溫控范圍(15~25℃),長期穩定度±0.2℃;寬溫控范圍(5~40℃),長期穩定度±0.4℃;顯然,這與不超過±0.1℃的技術要求存在差距。
上述自調系統的誤差源經開環檢測,主要是橋式溫度-電壓變換電路的電源電壓EO的穩定度,電橋輸出放大器的零點漂移,其次是可控恒流源的電流漂移。
4 建立微機溫度雙回路數字測控系統
圖1所示的系統是單回路自動控制系統,在此基礎上,再加入一個以微機為核心的測控回路,構成雙回路數字測控系統,該系統如圖6所示。圖6 中,PC是單片機,鍵盤、顯示器為人、機界面。溫度精測電路可實現比圖1的測溫電路更精確的溫度測量。然后經模/數轉換,PC進行數據處理。并依據輸出溫度與設定溫度的偏差,PC經數/模轉換給出微調值。這是一個負反饋的過程。
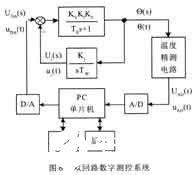
圖6所示系統提高溫控精度的主要措施有以下幾點。
4.1 應用電阻比較法,提高測溫精度
將圖3電路中的R0、 RT 電橋臂直接用微機進行檢測,電原理圖如圖7所示。
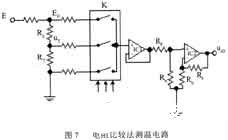
圖中:IC1為高阻輸入射隨器,保證對 R0、RT測量不分流。IC2為差動放大器,可較好地消弱共模噪聲電壓。IC2放大倍數KC2決定于計算機A/D 轉換量程。控制up2 數字信號,分別測量EO,u T,則
![]()
由于uT、E0是直接測量所得。盡管由于 E的變化引起UT、E0 的相應變化,微機(通過A/D轉換)仍能準確測量瞬時值。由于測量速度很快,兩次測量可認為放大器增益KC2變化極小。因而,通過式(14)可精確計算RT值,且測量精度與 E的變化和KC2的變化無關,只決定于 uT、E0的檢測精度和 R0的精度。必須指出的是,這種電阻比較法,只適用于微機測量。這是本文提出的新方法。
4.2 應用數字濾波和零點補償,有效消弱放大器的零點漂移
為消弱測量UT、 E0的隨機誤差和放大器的零漂,使測量精度進一步提高,采用數字濾波和零點補償法。測量數學模型為:
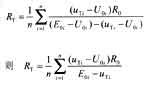
式中:n 為測量次數;E0i、U Ti和U0i分別為第i次測量E0、u T和U0值。U0 為IC1、IC2的零位電壓,可以通過模擬開關K使IC1接地進行測量。測量精度可達0.1%,相對溫度誤差±0.02℃。
4.3 應用單片機進行補償
在圖6所示的數字溫控(微調)過程中,單片機是按一定采樣周期進行調整的。設UDAS 為給定或要求達到的給定電壓值,UDAS (N)為任意第N 個采樣周期的UDAS值。同樣,設U DA 為實測(或采樣)的電壓值,UDA (N)為任意第N 個采樣周期的UDA值。為了達到精密的測控 [4],微機依據UDA(N )與UDAS(N)的差,通過D/A 轉換器給出負反饋特征的調整量,使UDA 向接近UDAS變化,向消除兩者之差的方向變化。同時考慮 UDA 隨時間的變化速率,還要考慮UDA( N)與其前一周期UDA(N- 1 )的變化。因而總的電壓調整增量應為:ΔU=U DAS(N)+UDA(N -1)-2UDA(N)。這就是微機進行微調補償的數學模型。
通過上述一系列措施,使圖6給出的雙回路溫控系統的溫控范圍達到10~35℃、溫控精度達到±0.03~±0.05℃,滿足了寬范圍、高精度的要求。
5 結束語
本文所述的溫控電路,已成功的應用于EDFA 模塊的溫度測控。達到了預期要求的寬范圍(10~35℃)、高精度(±0.03~±0.05℃)、高可靠性。所有實用化的EDFA產品,經過近5年的現場運行,都未出現任何問題。
責任編輯:gt
-
溫度傳感器
+關注
關注
48文章
2974瀏覽量
156300 -
激光器
+關注
關注
17文章
2539瀏覽量
60582
發布評論請先 登錄
相關推薦
小電流?高精度!大牛傳授電流檢測放大器應用電路設計
三相電機高精度寬范圍交流電測量包括BOM及層圖
實現高精度電流測量的30A寬共模范圍/雙向分流監控器參考設計
一種高精度、寬動態范圍的APD偏壓控制/光功率監測電路設計
基于霍爾傳感器的高精度測速電路設計
如何進行高精度寬范圍恒流源電路的設計




 基于EDFA模塊實現高精度、寬范圍的溫控電路設計
基于EDFA模塊實現高精度、寬范圍的溫控電路設計












評論