技巧一:為電源選擇正確的工作頻率
為電源選擇最佳的工作頻率是一個復雜的權衡過程,其中包括尺寸、效率以及成本。通常來說,低頻率設計往往是最為高效的,但是其尺寸最大且成本也最高。雖然調高頻率可以縮小尺寸并降低成本,但會增加電路損耗。接下來,我們使用一款簡單的降壓電源來描述這些權衡過程。
我們以濾波器組件作為開始。這些組件占據了電源體積的大部分,同時濾波器的尺寸同工作頻率成反比關系。另一方面,每一次開關轉換都會伴有能量損耗;工作頻率越高,開關損耗就越高,同時效率也就越低。其次,較高的頻率運行通常意味著可以使用較小的組件值。因此,更高頻率運行能夠帶來極大的成本節約。
圖1.1顯示的是降壓電源頻率與體積的關系。頻率為100 kHz時,電感占據了電源體積的大部分(深藍色區域)。如果我們假設電感體積與其能量相關,那么其體積縮小將與頻率成正比例關系。由于某種頻率下電感的磁芯損耗會極大增高并限制尺寸的進一步縮小,因此在此情況下上述假設就不容樂觀了。如果該設計使用陶瓷電容,那么輸出電容體積(褐色區域)便會隨頻率縮小,即所需電容降低。另一方面,之所以通常會選用輸入電容,是因為其具有紋波電流額定值。該額定值不會隨頻率而明顯變化,因此其體積(黃色區域)往往可以保持恒定。另外,電源的半導體部分不會隨頻率而變化。這樣,由于低頻開關,無源器件會占據電源體積的大部分。當我們轉到高工作頻率時,半導體(即半導體體積,淡藍色區域)開始占據較大的空間比例。
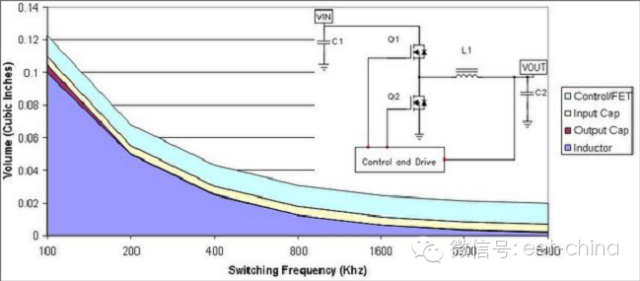
圖1.1 電源組件體積主要由半導體占據
該曲線圖顯示半導體體積本質上并未隨頻率而變化,而這一關系可能過于簡單化。與半導體相關的損耗主要有兩類:傳導損耗和開關損耗。同步降壓轉換器中的傳導損耗與 MOSFET 的裸片面積成反比關系。MOSFET 面積越大,其電阻和傳導損耗就越低。
開關損耗與MOSFET 開關的速度以及MOSFET 具有多少輸入和輸出電容有關。這些都與器件尺寸的大小相關。大體積器件具有較慢的開關速度以及更多的電容。圖1.2 顯示了兩種不同工作頻率 (F) 的關系。傳導損耗 (Pcon) 與工作頻率無關,而開關損耗 (Psw F1 和Psw F2) 與工作頻率成正比例關系。因此更高的工作頻率 (Psw F2) 會產生更高的開關損耗。當開關損耗和傳導損耗相等時,每種工作頻率的總損耗最低。另外,隨著工作頻率提高,總損耗將更高。
但是,在更高的工作頻率下,最佳裸片面積較小,從而帶來成本節約。實際上,在低頻率下,通過調整裸片面積來最小化損耗會帶來極高成本的設計。但是,轉到更高工作頻率后, 我們就可以優化裸片面積來降低損耗,從而縮小電源的半導體體積。這樣做的缺點是,如果我們不改進半導體技術,那么電源效率將會降低。
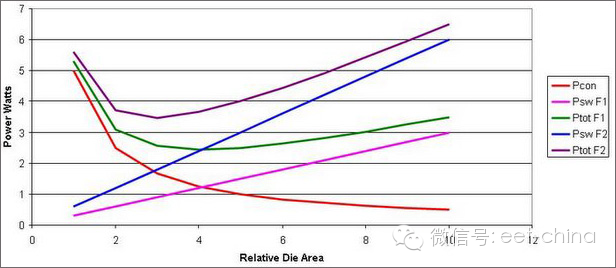
圖1.2 提高工作頻率會導致更高的總體損耗
如前所述,更高的工作頻率可縮小電感體積;所需的內層芯板會減少。更高頻率還可降低對于輸出電容的要求。有了陶瓷電容,我們就可以使用更低的電容值或更少的電容。這有助于縮小半導體裸片面積,進而降低成本。
技巧二:駕馭噪聲電源
無噪聲電源并非是偶然設計出來的。一種好的電源布局是在設計時最大程度的縮短實驗時間。花費數分鐘甚至是數小時的時間來仔細查看電源布局,便可以省去數天的故障排查時間。
圖2.1顯示的是電源內部一些主要噪聲敏感型電路的結構圖。將輸出電壓與一個參考電壓進行比較以生成一個誤差信號,然后再將該信號與一個斜坡相比較,以生成一個用于驅動功率級的PWM(脈寬調制)信號。
電源噪聲主要來自三個地方:誤差放大器輸入與輸出、參考電壓以及斜坡。對這些節點進行精心的電氣設計和物理設計有助于最大程度地縮短故障診斷時間。一般而言,噪聲會與這些低電平電路電容耦合。一種卓越的設計可以確保這些低電平電路的緊密布局,并遠離所有開關波形。接地層也具有屏蔽作用。
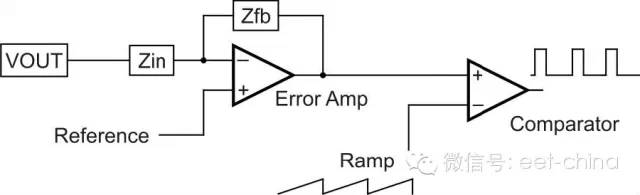
圖 2.1 低電平控制電路的諸多噪聲形成機會
誤差放大器輸入端可能是電源中最為敏感的節點,因為其通常具有最多的連接組件。如果將其與該級的極高增益和高阻抗相結合,后患無窮。在布局過程中,您必須最小化節點長度,并盡可能近地將反饋和輸入組件靠近誤差放大器放置。如果反饋網絡中存在高頻積分電容,那么您必須將其靠近放大器放置,其他反饋組件緊跟其后。并且,串聯電阻-電容也可能形成補償網絡。最理想的結果是,將電阻靠近誤差放大器輸入端放置,這樣,如果高頻信號注入該電阻-電容節點時,那么該高頻信號就不得不承受較高的電阻阻抗—而電容對高頻信號的阻抗則很小。
斜坡是另一個潛在的會帶來噪聲問題的地方。斜坡通常由電容器充電(電壓模式)生成,或由來自于電源開關電流的采樣(電流模式)生成。通常,電壓模式斜坡并不是一個問題。
因為電容對高頻注入信號的阻抗很小。而電流斜坡卻較為棘手,因為存在了上升邊沿峰值、相對較小的斜坡振幅以及功率級寄生效應。
圖2.2顯示了電流斜坡存在的一些問題。第一幅圖顯示了上升邊沿峰值和隨后產生的電流斜坡。比較器(根據其不同速度)具有兩個電壓結點 (potential trip points),結果是無序控制運行,聽起來更像是煎熏肉的聲音。
利用控制IC中的上升邊沿消隱可以很好地解決這一問題,其忽略了電流波形的最初部分。波形的高頻濾波也有助于解決該問題。同樣也要將電容器盡可能近地靠近控制IC放置。正如這兩種波形表現出來的那樣,另一種常見的問題是次諧波振蕩。這種寬-窄驅動波形表現為非充分斜率補償。向當前斜坡增加更多的電壓斜坡便可以解決該問題。
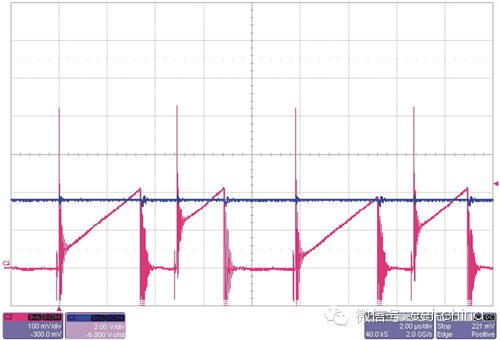
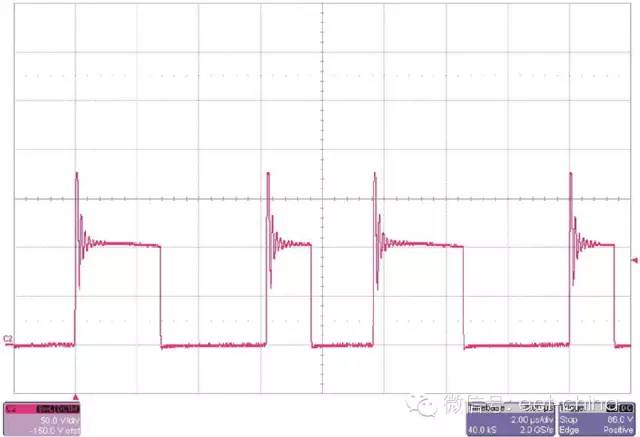
圖2.2 兩種常見的電流模式噪聲問題
盡管您已經相當仔細地設計了電源布局,但是您的原型電源還是存在噪聲。這該怎么辦呢?首先,您要確定消除不穩定因素的環路響應不存在問題。有趣的是,噪聲問題可能會看起來像是電源交叉頻率上的不穩定。但真正的情況是該環路正以其最快響應速度糾出注入誤差。同樣,最佳方法是識別出噪聲正被注入下列三個地方之一:誤差放大器、參考電壓或斜坡。您只需分步解決便可!
第一步是檢查節點,看斜坡中是否存在明顯的非線性,或者誤差放大器輸出中是否存在高頻率變化。如果檢查后沒有發現任何問題,那么就將誤差放大器從電路中取出,并用一個清潔的電壓源加以代替。這樣您應該就能夠改變該電壓源的輸出,以平穩地改變電源輸出。如果這樣做奏效的話,那么您就已經將問題范圍縮小至參考電壓和誤差放大器了。
有時,控制IC中的參考電壓易受開關波形的影響。利用添加更多(或適當)的旁路可能會使這種狀況得到改善。另外,使用柵極驅動電阻來減緩開關波形也可能會有助于解決這一問題。如果問題出在誤差放大器上,那么降低補償組件阻抗會有所幫助,因為這樣降低了注入信號的振幅。如果所有這些方法都不奏效,那么就從印刷電路板將誤差放大器節點去除。對補償組件進行架空布線 (air wiring) 可以幫助我們識別出哪里有問題。
技巧三:阻尼輸入濾波系列
開關調節器通常優于線性調節器,因為它們更高效,而開關拓撲結構則十分依賴輸入濾波器。這種電路元件與電源的典型負動態阻抗相結合,可以誘發振蕩問題。本文將闡述如何避免此類問題的出現。
一般而言,所有的電源都在一個給定輸入范圍保持其效率。因此,輸入功率或多或少地與輸入電壓水平保持恒定。圖3.1顯示的是一個開關電源的特征。隨著電壓的下降,電流不斷上升。
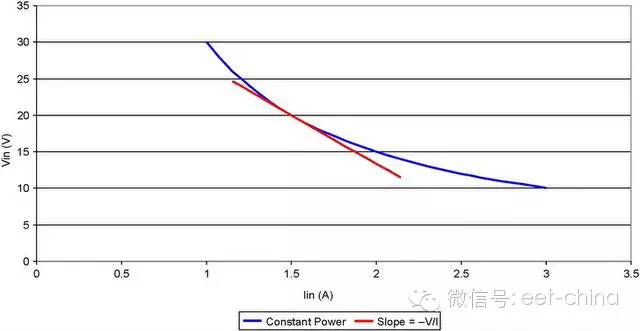
圖3.1 開關電源表現出的負阻抗
負輸入阻抗
電壓-電流線呈現出一定的斜率,其從本質上定義了電源的動態阻抗。這根線的斜率等于負輸入電壓除以輸入電流。也就是說,由Pin=V?I,可以得出V=Pin/I;并由此可得dV/dI=–Pin/I2或dV/dI≈–V/I。
該近似值有些過于簡單,因為控制環路影響了輸入阻抗的頻率響應。但是很多時候,當涉及電流模式控制時這種簡單近似值就已足夠了。
為什么需要輸入濾波器
開關調節器輸入電流為非連續電流,并且在輸入電流得不到濾波的情況下其會中斷系統的運行。大多數電源系統都集成了一個如圖3.2所示類型的濾波器。電容為功率級的開關電流提供了一個低阻抗,而電感則為電容上的紋波電壓提供了一個高阻抗。該濾波器的高阻抗使流入源極的開關電流最小化。在低頻率時,該濾波器的源極阻抗等于電感阻抗。在您升高頻率的同時,電感阻抗也隨之增加。在極高頻率時,輸出電容分流阻抗。在中間頻率時,電感和電容實質上就形成了一種并聯諧振電路,從而使電源阻抗變高,呈現出較高的電阻。
大多數情況下,峰值電源阻抗可以通過首先確定濾波器 (Zo) 的特性阻抗來估算得出,而濾波器特性阻抗等于電感除以電容所得值的平方根。這就是諧振下電感或者電容的阻抗。接下來,對電容的等效串聯電阻 (ESR) 和電感的電阻求和。這樣便得到電路的Q值。峰值電源阻抗大約等于Zo乘以電路的Q值。
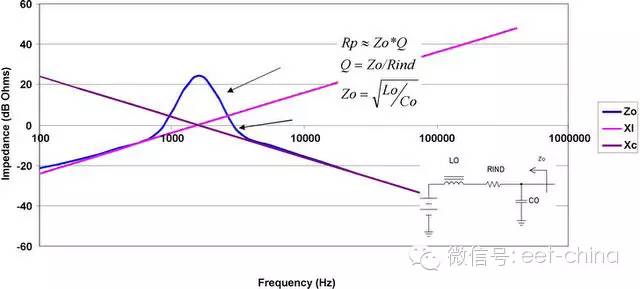
圖3.2 諧振時濾波器的高阻抗和高阻性
振 蕩
但是,開關的諧振濾波器與電源負阻抗耦合后會出現問題。圖3.3顯示的是在一個電壓驅動串聯電路中值相等、極性相反的兩個電阻。這種情況下,輸出電壓趨向于無窮大。當您獲得由諧振輸入濾波器等效電阻所提供電源的負電阻時,您也就會面臨一個類似的電源系統情況;這時,電路往往就會出現振蕩。
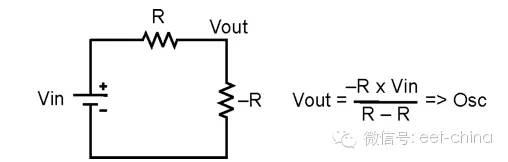
圖3.3 與其負阻抗耦合的開關諧振濾波器可引起不必要的振蕩
設計穩定電源系統的秘訣是保證系統電源阻抗始終大大小于電源的輸入阻抗。我們需要在最小輸入電壓和最大負載(即最低輸入阻抗)狀態下達到這一目標。
控制源極阻抗
在前面,我們討論了輸入濾波器的源極阻抗如何變得具有電阻性,以及其如何同開關調節器的負輸入阻抗相互作用。在極端情況下,這些阻抗振幅可以相等,但是其符號相反從而構成了一個振蕩器。業界通用的標準是輸入濾波器的源極阻抗應至少比開關調節器的輸入阻抗低6dB,作為最小化振蕩概率的安全裕度。
輸入濾波器設計通常以根據紋波電流額定值或保持要求選擇輸入電容(圖4.1所示CO)開始的。第二步通常包括根據系統的EMI要求選擇電感 (LO)。正如我們上個月討論的那樣,在諧振附近,這兩個組件的源極阻抗會非常高,從而導致系統不穩定。圖 1 描述了一種控制這種阻抗的方法,其將串聯電阻 (RD) 和電容 (CD) 與輸入濾波器并聯放置。利用一個跨接 CO 的電阻,可以阻尼濾波器。但是,在大多數情況下,這樣做會導致功率損耗過高。另一種方法是在濾波器電感的兩端添加一個串聯連接的電感和電阻。
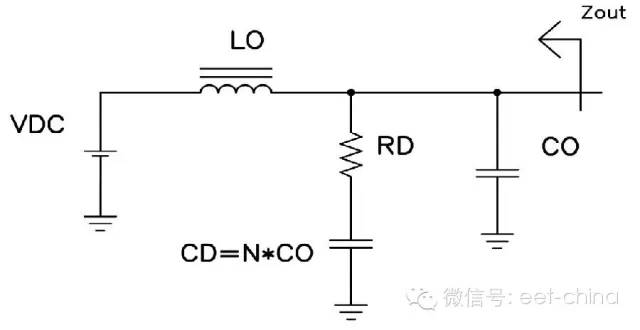
圖4.1 CD和RD阻尼輸出濾波器源極阻抗
選擇阻尼電阻
有趣的是,一旦選擇了四個其他電路組件,那么就會有一個阻尼電阻的最佳選擇。圖4.2 顯示的是不同阻尼電阻情況下這類濾波器的輸出阻抗。紅色曲線表示過大的阻尼電阻。請思考一下極端的情況,如果阻尼電阻器開啟,那么峰值可能會非常的高,且僅由CO和LO來設定。藍色曲線表示阻尼電阻過低。如果電阻被短路,則諧振可由兩個電容和電感的并聯組合共同設置。綠色曲線代表最佳阻尼值。利用一些包含閉型解的計算方法(見參考文獻 1)就可以很輕松地得到該值。
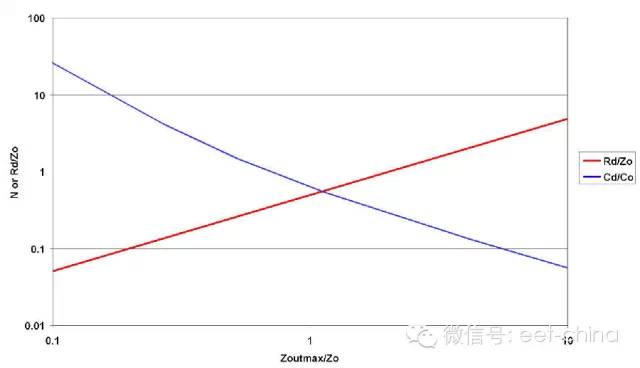
圖4.2 在給定CD-CO比的情況下,有一個最佳阻尼電阻
選擇組件
在選擇阻尼組件時,圖4.3非常有用。該圖是通過使用RD Middlebrook建立的閉型解得到的。橫坐標為阻尼濾波器輸出阻抗與未阻尼濾波器典型阻抗 (ZO= (LO/CO)1/2) 的比。縱坐標值有兩個:阻尼電容與濾波器電容 (N) 的比;以及阻尼電阻同該典型阻抗的比。利用該圖,首先根據電路要求來選擇LO和CO,從而得到ZO。隨后,將最小電源輸入阻抗除以二,得到您的最大輸入濾波器源極阻抗 (6dB)。
最小電源輸入阻抗等于Vinmin2/Pmax。只需讀取阻尼電容與濾波器電容的比以及阻尼電阻與典型阻抗的比, 您便可以計算得到一個橫坐標值。例如,一個具有10μH電感和10μH 電容的濾波器具有Zo= (10μH/10μF)1/2=1Ohm 的典型阻抗。如果它正對一個12V最小輸入的12W電源進行濾波,那么該電源輸入阻抗將為Z=V2/P=122/12=12Ohms。這樣,最大源極阻抗應等于該值的二分之一,也即6Ohms。現在,在6/1=6的X軸上輸入該圖,那么,CD/CO=0.1,即1μF,同時RD/ZO=3,也即3Ohms。

圖4.3 選取LO和CO后,便可從最大允許源極阻抗范圍內選擇CD和RD
技巧四:升壓電源設計中降壓控制器的使用
電子電路通常都工作在正穩壓輸出電壓下,而這些電壓一般都是由降壓穩壓器來提供的。如果同時還需要負輸出電壓,那么在降壓—升壓拓撲中就可以配置相同的降壓控制器。負輸出電壓降壓—升壓有時稱之為負反向,其工作占空比為50%,可提供相當于輸入電壓但極性相反的輸出電壓。其可以隨著輸入電壓的波動調節占空比,以“降壓”或“升壓”輸出電壓來維持穩壓。
圖 5.1顯示了一款精簡型降壓—升壓電路,以及電感上出現的開關電壓。這樣一來該電路與標準降壓轉換器的相似性就會頓時明朗起來。實際上,除了輸出電壓和接地相反以外,它和降壓轉換器完全一樣。這種布局也可用于同步降壓轉換器。這就是與降壓或同步降壓轉換器端相類似的地方,因為該電路的運行與降壓轉換器不同。
FET開關時出現在電感上的電壓不同于降壓轉換器的電壓。正如在降壓轉換器中一樣,平衡伏特-微秒 (V-μs) 乘積以防止電感飽和是非常必要的。當FET為開啟時(如圖 1 所示的ton間隔),全部輸入電壓被施加至電感。這種電感“點”側上的正電壓會引起電流斜坡上升,這就帶來電感的開啟時間V-μs乘積。FET 關閉 (toff) 期間,電感的電壓極性必須倒轉以維持電流,從而拉動點側為負極。電感電流斜坡下降,并流經負載和輸出電容,再經二極管返回。電感關閉時V-μs乘積必須等于開啟時V-μs乘積。由于Vin和Vout不變,因此很容易便可得出占空比 (D) 的表達式:D=Vout/(Vout " Vin)。這種控制電路通過計算出正確的占空比來維持輸出電壓穩壓。上述表達式和圖5.1所示波形均假設運行在連續導電模式下。
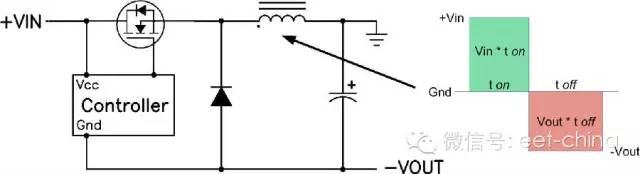
圖 5.1 降壓—升壓電感要求平衡其伏特-微秒乘積
降壓—升壓電感必須工作在比輸出負載電流更高的電流下。其被定義為IL=I
有趣的是,連接輸入電容返回端的方法有兩種,其會影響輸出電容的rms電流。典型的電容布局是在+Vin和Gnd之間,與之相反,輸入電容可以連接在+Vin和 "V
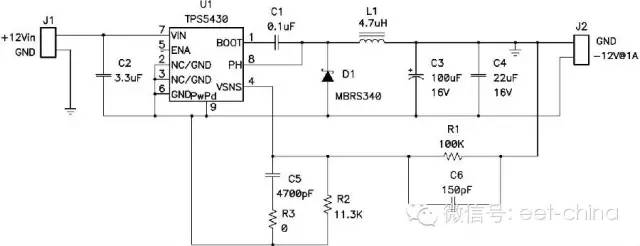
圖5.2 降壓控制器在降壓—升壓中的雙重作用
必須要選擇一個能夠以最小輸入電壓減去二極管壓降上電的控制器,而且在運行期間還必須能夠承受得住Vin加Vout的電壓。FET和二極管還必須具有適用于這一電壓范圍的額定值。通過連接輸出接地的反饋電阻器可實現對輸出電壓的調節,這是由于控制器以負輸出電壓為參考電壓。只需精心選取少量組件的值,并稍稍改動電路,降壓控制器便可在負輸出降壓—升壓拓撲中起到雙重作用。
技巧五:精確測量電源紋波
精確地測量電源紋波本身就是一門藝術。在圖6.1所示的示例中,一名初級工程師完全錯誤地使用了一臺示波器。他的第一個錯誤是使用了一支帶長接地引線的示波器探針;他的第二個錯誤是將探針形成的環路和接地引線均置于電源變壓器和開關元件附近;他的最后一個錯誤是允許示波器探針和輸出電容之間存在多余電感。該問題在紋波波形中表現為高頻拾取。在電源中,存在大量可以很輕松地與探針耦合的高速、大信號電壓和電流波形,其中包括耦合自電源變壓器的磁場,耦合自開關節點的電場,以及由變壓器互繞電容產生的共模電流。
圖 6.1 錯誤的紋波測量得到的較差的測量結果
利用正確的測量方法可以大大地改善測得紋波結果。首先,通常使用帶寬限制來規定紋波,以防止拾取并非真正存在的高頻噪聲。我們應該為用于測量的示波器設定正確的帶寬限制。其次,通過取掉探針“帽”,并構成一個拾波器(如圖6.2所示),我們可以消除由長接地引線形成的天線。將一小段線纏繞在探針接地連接點周圍,并將該接地連接至電源。這樣做可以縮短暴露于電源附近高電磁輻射的端頭長度,從而進一步減少拾波。
最后,在隔離電源中,會產生大量流經探針接地連接點的共模電流。這就在電源接地連接點和示波器接地連接點之間形成了壓降,從而表現為紋波。要防止這一問題的出現,我們就需要特別注意電源設計的共模濾波。另外,將示波器引線纏繞在鐵氧體磁心周圍也有助于最小化這種電流。這樣就形成了一個共模電感器,其在不影響差分電壓測量的同時,還減少了共模電流引起的測量誤差。圖6.2顯示了該完全相同電路的紋波電壓,其使用了改進的測量方法。這樣,高頻峰值就被真正地消除了。
圖6.2 四個輕微的改動便極大地改善了測量結果
實際上,集成到系統中以后,電源紋波性能甚至會更好。在電源和系統其他組件之間幾乎總是會存在一些電感。這種電感可能存在于布線中,抑或只有蝕刻存在于PWB上。另外,在芯片周圍總是會存在額外的旁路電容,它們就是電源的負載。這二者共同構成一個低通濾波器,進一步降低了電源紋波和/或高頻噪聲。在極端情況下,電流短時流經15nH電感和 10μF旁路電容的一英寸導體時,該濾波器的截止頻率為400kHz。這種情況下,就意味著高頻噪聲將會得到極大降低。許多情況下,該濾波器的截止頻率會在電源紋波頻率以下,從而有可能大大降低紋波。經驗豐富的工程師應該能夠找到在其測試過程中如何運用這種方法的途徑。
技巧六:高效驅動LED離線式照明
用切實可行的螺紋旋入式LED來替代白熾燈泡可能還需要數年的時間,而在建筑照明中LED的使用正在不斷增長,其具有更高的可靠性和節能潛力。同大多數電子產品一樣,其需要一款電源來將輸入功率轉換為LED可用的形式。在路燈應用中,一種可行的配置是創建300V/0.35安培負載的80個串聯的LED。在選擇電源拓撲結構時,需要制定隔離和功率因數校正 (PFC) 相關要求。隔離需要大量的安全權衡研究,其中包括提供電擊保護需求和復雜化電源設計之間的對比權衡。在這種應用中,LED上存在高壓,一般認為隔離是非必需的,而PFC才是必需的,因為在歐洲25瓦以上的照明均要求具有PFC功能,而這款產品正是針對歐洲市場推出的。
就這種應用而言,有三種可選電源拓撲:降壓拓撲、轉移模式反向拓撲和轉移模式 (TM) 單端初級電感轉換器 (SEPIC) 拓撲。當LED電壓大約為80伏特時,降壓拓撲可以非常有效地被用于滿足諧波電流要求。在這種情況下,更高的負載電壓將無法再繼續使用降壓拓撲。那么,此時較為折中的方法就是使用反向拓撲和SEPIC拓撲。SEPIC 具有的優點是,其可鉗制功率半導體器件的開關波形,允許使用較低的電壓,從而使器件更為高效。在該應用中,可以獲得大約2%的效率提高。另外,SEPIC中的振鈴更少,從而使EMI濾波更容易。圖7.1 顯示了這種電源的原理圖。
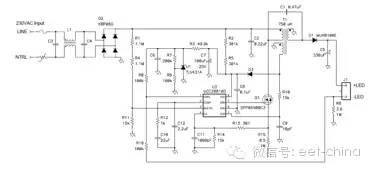
圖7.1 轉移模式SEPIC發揮了簡單LED驅動器的作用
該電路使用了一個升壓TM PFC控制器來控制輸入電流波形。該電路以離線為C6充電作為開始。一旦開始工作,控制器的電源就由一個SEPIC電感上的輔助繞組來提供。一個相對較大的輸出電容將LED紋波電流限定在DC電流的20%。補充說明一下,TM SEPIC中的AC 電通量和電流非常高,需要漆包絞線和低損耗內層芯板來降低電感損耗。
圖7.2和圖7.3顯示了與圖7.1中原理圖相匹配的原型電路的實驗結果。與歐洲線路范圍相比,其效率非常之高,最高可達92%。這一高效率是通過限制功率器件上的振鈴實現的。另外,正如我們從電流波形中看到的一樣,在96%效率以上時功率因數非常好。有趣的是,該波形并非純粹的正弦曲線,而是在上升沿和下降沿呈現出一些斜度,這是電路沒有測量輸入電流而只對開關電流進行測量的緣故。但是,該波形還是足以通過歐洲諧波電流要求的。
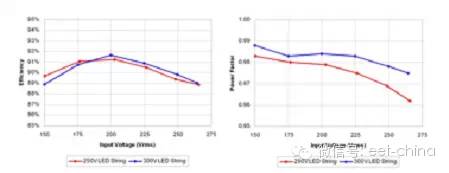
圖7.2 TM SEPIC具有良好的效率和高PFC效率
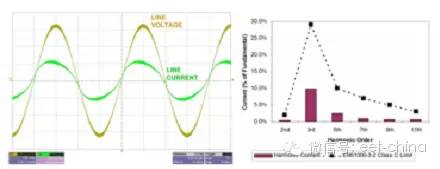
圖7.3 線路電流輕松地通過 EN61000-3-2 Class C標準
技巧七:通過改變電源頻率來降低EMI性能
在測定EMI性能時,您是否發現無論您采用何種方法濾波都依然會出現超出規范幾dB 的問題呢?有一種方法或許可以幫助您達到EMI性能要求,或簡化您的濾波器設計。這種方法涉及了對電源開關頻率的調制,以引入邊帶能量,并改變窄帶噪聲到寬帶的發射特征,從而有效地衰減諧波峰值。需要注意的是,總體 EMI 性能并沒有降低,只是被重新分布了。
利用正弦調制,可控變量的兩個變量為調制頻率 (fm) 以及您改變電源開關頻率 (Δf) 的幅度。調制指數 (Β) 為這兩個變量的比:
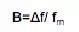
圖8.1顯示了通過正弦波改變調制指數產生的影響。當Β=0時,沒有出現頻移,只有一條譜線。當Β=1時,頻率特征開始延伸,且中心頻率分量下降了20%。當Β=2時,該特征將進一步延伸,且最大頻率分量為初始狀態的60%。頻率調制理論可以用于量化該頻譜中能量的大小。Carson法則表明大部分能量都將被包含在2 * (Δf + fm) 帶寬中。
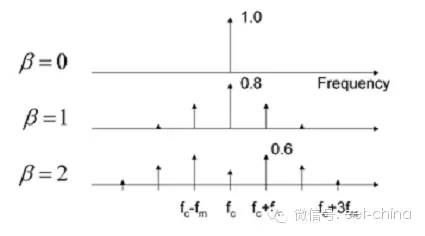
圖8.1 調制電源開關頻率延伸了EMI特征
圖8.2顯示了更大的調制指數,并表明降低12dB以上的峰值EMI性能是有可能的。
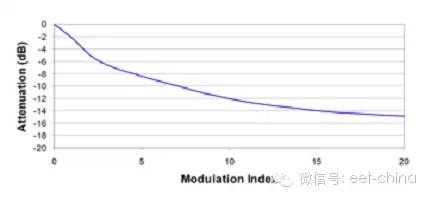
圖8.2 更大的調制指數可以進一步降低峰值EMI性能
選取調制頻率和頻移是兩個很重要的方面。首先,調制頻率應該高于EMI接收機帶寬,這樣接收機才不會同時對兩個邊帶進行測量。但是,如果您選取的頻率太高,那么電源控制環路可能無法完全控制這種變化,從而帶來相同速率下的輸出電壓變化。另外,這種調制還會引起電源中出現可聞噪聲。因此,我們選取的調制頻率一般不能高出接收機帶寬太多,但要大于可聞噪聲范圍。很顯然,從圖8.2我們可以看出,較大地改變工作頻率更為可取。然而,這樣會影響到電源設計,意識到這一點非常重要。也就是說,為最低工作頻率選擇磁性元件。此外,輸出電容還需要處理更低頻率運行帶來的更大的紋波電流。
圖8.3對有頻率調制和無頻率調制的EMI性能測量值進行了對比。此時的調制指數為4,正如我們預料的那樣,基頻下EMI性能大約降低了8dB。其他方面也很重要。諧波被抹入 (smear into) 同其編號相對應的頻帶中,即第三諧波延展至基頻的三倍。這種情況會在一些較高頻率下重復,從而使噪聲底限大大高于固定頻率的情況。因此,這種方法可能并不適用于低噪聲系統。但是,通過增加設計裕度和最小化EMI濾波器成本,許多系統都已受益于這種方法。
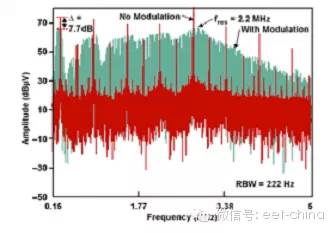
圖8.3 改變電源頻率降低了基頻但提高了噪聲底限
技巧八:估算表面貼裝半導體的溫升
過去估算半導體溫升十分簡單。您只需計算出組件的功耗,然后采用冷卻電路電模擬即可確定所需散熱片的類型。現在出于對尺寸和成本因素的考慮,人們渴望能夠去除散熱片,這就使得這一問題復雜化了。貼裝在散熱增強型封裝中的半導體要求電路板能夠起到散熱片的作用,并提供所有必需的冷卻功能。如圖9.1所示,熱量經過一塊金屬貼裝片和封裝流入印刷線路板 (PWB)。然后,熱量由側面流經PWB線跡,并通過自然對流經電路板表面擴散到周圍的環境中。影響裸片溫升的重要因素是PWB中的銅含量以及用于對流導熱的表面面積。
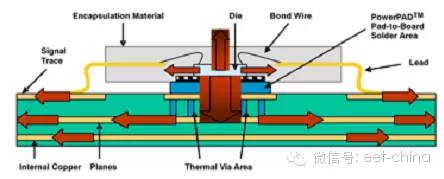
圖9.1 熱量由側面流經PWB線跡,然后從 PWB 表面擴散至周圍環境
半導體產品說明書通常會列出某種PWB結構下結點至周圍環境的熱阻。這就是說,設計人員只需將這種熱阻乘以功耗,便可計算出溫升情況。但是,如果設計并沒有具體的結構,或者如果需要進一步降低熱阻,那么就會出現許多問題。
圖9.2所示為熱流問題的簡化電模擬,我們可據此深入分析。IC電源由電流源表示,而熱阻則由電阻表示。在各電壓下對該電路求解,其提供了對溫度的模擬。從結點至貼裝面存在熱阻,同時遍布于電路板的橫向電阻和電路板表面至周圍環境的電阻共同形成一個梯形網絡。這種模型假設:1)電路板為垂直安裝,2)無強制對流或輻射制冷,所有熱流均出現在電路板的銅中,3)在電路板兩側幾乎沒有溫差。
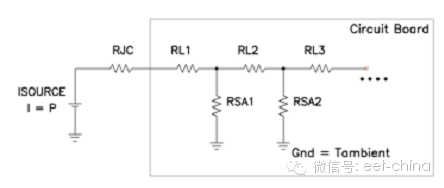
圖9.2 熱流電氣等效簡化了溫升估算
圖9.3所示為增加PWB中的銅含量對提高熱阻的影響。將1.4 mils銅(雙面,半盎司)增加到8.4 mils(4層,1.5盎司),就有可能將熱阻提高3倍。圖中兩條曲線:一條表示熱流進入電路板、直徑為0.2英寸的小尺寸封裝;另一條表示熱流進入電路板、直徑為0.4英寸的大尺寸封裝。這兩條曲線均適用于9平方英寸的PWB。這兩條曲線均同標稱數據緊密相關,同時都有助于估算改變產品說明書電路板結構所產生的影響。但是使用這一數據時需要多加謹慎,其假設9平方英寸PWB內沒有其他功耗,而實際上并非如此。
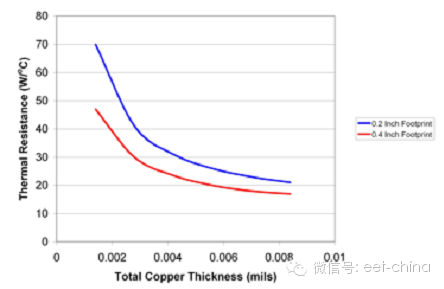
圖9.3 熱流電氣等效簡化了溫升估算
技巧九:輕松估計負載瞬態響應
本篇電源設計小貼士介紹了一種通過了解控制帶寬和輸出濾波器電容特性估算電源瞬態響應的簡單方法。該方法充分利用了這樣一個事實,即所有電路的閉環輸出阻抗均為開環輸出阻抗除以 1 加環路增益,或簡單表述為:

圖10.1以圖形方式說明了上述關系,兩種阻抗均以dB-Ω或20*log [Z]為單位。在開環曲線上的低頻率區域內,輸出阻抗取決于輸出電感阻抗和電感。當輸出電容和電感發生諧振時,形成峰值。高頻阻抗取決于電容輸出濾波器特性、等效串聯電阻 (ESR) 以及等效串聯電感 (ESL)。將開環阻抗除以1加環路增益即可計算得出閉環輸出阻抗。
由于該圖形以對數表示,即簡單的減法,因此在增益較高的低頻率區域阻抗會大大降低;在增益較少的高頻率區域閉環和開環阻抗基本上是一樣的。在此需要說明如下要點:1)峰值環路阻抗出現在電源交叉頻率附近,或出現在環路增益等于1(或0dB)的地方;以及2)在大部分時間里,電源控制帶寬都將會高于濾波器諧振,因此峰值閉環阻抗將取決于交叉頻率時的輸出電容阻抗。

圖10.1閉環輸出阻抗峰值Zout出現在控制環路交叉頻率處
一旦知道了峰值輸出阻抗,就可通過負載變動幅度與峰值閉環阻抗的乘積來輕松估算瞬態響應。有幾點注意事項需要說明一下,由于低相位裕度會引起峰化,因此實際的峰值可能會更高些。然而,就快速估計而言,這種影響可以忽略不計 。
第二個需要注意的事項與負載變化幅度上升有關。如果負載變化幅度變化緩慢(dI/dt較低),則響應取決于與上升時間有關的低頻率區域閉環輸出阻抗;如果負載變化幅度變化極為快速,則輸出阻抗將取決于輸出濾波器ESL。如果確實如此,則可能需要更多的高頻旁通。最后,就極高性能的系統而言,電源的功率級可能會限制響應時間,即電感器中的電流可能不能像控制環路期望的那樣快速響應,這是因為電感和施加的電壓會限制電流轉換速率。
下面是一個如何使用上述關系的示例。問題是根據200kHz開關電源10amp變化幅度允許范圍內的50mV輸出變化挑選一個輸出電容。所允許的峰值輸出阻抗為:Zout=50mV/10 amps或5毫歐。這就是最大允許輸出電容ESR。接下來就是建立所需的電容。幸運的是,ESR和電容均為正交型,可單獨處理。一個高 (Aggressive) 電源控制環路帶寬可以是開關頻率的1/6或30 kHz。于是在30 kHz 時輸出濾波電容就需要一個不到5毫歐的電抗,或高于1000uF的電容。圖10.2顯示了在5毫歐ESR、1000uF電容以及30kHz 電壓模式控制條件時這一問題的負載瞬態仿真。就校驗這一方法是否有效的10amp負載變動幅度而言,輸出電壓變化大約為52mV。
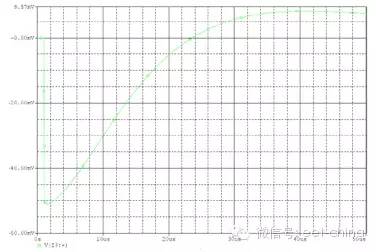
圖 10.2 仿真校驗估計負載瞬態性能
技巧十:輕松估計解決電源電路損耗問題
您是否曾詳細計算過設計中的預計組件損耗,結果卻發現與實驗室測量結果有較大出入呢?本電源設計小貼士介紹了一種簡便方法,以幫助您消除計算結果與實際測量結果之間的差異。該方法基于泰勒級數展開式,其中規定(在賦予一定自由條件下)任何函數都可分解成一個多項式,如下所示:
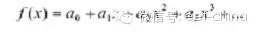
如果意識到電源損耗與輸出電流相關(可用輸出電流替換X),那么系數項就能很好地與不同來源的電源功率損耗聯系起來。例如,ao代表諸如柵極驅動、偏壓電源和磁芯的固定開銷損耗以及功率晶體管Coss充電與放電之類的損耗。這些損耗與輸出電流無關。第二項相關聯的損耗a1直接與輸出電流相關,其典型表現為輸出二極管損耗和開關損耗。在輸出二極管中,大多數損耗是由于結電壓引起的,因此損耗會隨著輸出電流成比例地增加。
類似地,開關損耗可通過輸出電流關聯項與某些固定電壓的乘積近似得出。第三項很容易被識別為傳導損耗。其典型表現為 FET 電阻、磁性布線電阻和互聯電阻中的損耗。高階項可能在計算非線性損耗(如磁芯損耗)時有用。只有在考慮前三項情況下才能得出有用結果。
計算三項系數的一種方法是測量三個工作點的損耗并成矩陣求解結果。如果損耗測量結果其中一項是在無負載的工況下得到(即所有損耗均等于第一項系數a0),那么就能簡化該解決方法。隨后問題簡化至容易求解的兩個方程式和兩個未知數。一旦計算出系數,即可構建出類似于圖11.1、顯示三種損耗類型的損耗曲線。該曲線在消除測量結果和計算結果之間的偏差時大有用處,并且有助于確定能夠提高效率的潛在區域。例如,在滿負載工況下,圖 1中的損耗主要為傳導損耗。為了提高效率,就需要降低 FET 電阻、電感電阻和互聯電阻。
圖11.1:功率損耗組件與二次項系數相匹配
實際損耗與三項式之間的相關性非常好。圖11.2對同步降壓穩壓器的測量數據與曲線擬合數據進行了對比。我們知道,在基于求解三個聯立方程組的曲線上將存在三個重合點。對于曲線的剩余部分,兩個曲線之間的差異小于2%。由于工作模式(如連續或非連續)不同、脈沖跳頻或變頻運行等原因,其他類型的電源可能很難以如此匹配。這種方法并非絕對可靠,但是有助于電源設計人員理解實際電路損耗情況。
圖11.2 前三個損耗項提供了與測量值良好的相關性
最后篇:電源效率最大化
在上節,我們討論了如何利用泰勒級數 (Taylor series) 查找電源中的損耗源。在本篇電源設計技巧中,我們將討論如何使用相同的級數最大化特定負載電流的電源效率。上節中,我們建議使用如下輸出電流函數來計算電源損耗:

下一步是利用上述簡單表達式,并將其放入效率方程式中:
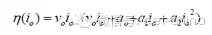
這樣,輸出電流的效率就得到了優化(具體論證工作留給學生去完成)。這種優化可產生一個有趣的結果。
當輸出電流等于如下表達式時,效率將會最大化。
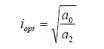
需要注意的第一件事是,a1項對效率達到最大時的電流不產生影響。這是由于它與損耗相關,而上述損耗又與諸如二極管結點的輸出電流成比例關系。因此,當輸出電流增加時,上述損耗和輸出功率也會隨之增加,并且對效率沒有影響。需要注意的第二件事是,最佳效率出現在固定損耗和傳導損耗相等的某個點上。這就是說,只要控制設置a0和a2值的組件,便能夠獲得最佳效率。還是要努力減小a1的值,并提高效率。控制該項所得結果對所有負載電流而言均相同,因此如其他項一樣沒有出現最佳效率。a1項的目標是在控制成本的同時達到最小化。
表1概括總結了各種電源損耗項及其相關損耗系數,該表提供了一些最佳化電源效率方面的折中方法。例如,功率MOSFET導通電阻的選擇會影響其柵極驅動要求及Coss損耗和潛在的緩沖器損耗。低導通電阻意味著,柵極驅動、Coss和緩沖器損耗逆向增加。因此,您可通過選擇 MOSFET 來控制a0和a2。
表1 損耗系數及相應的電源損耗
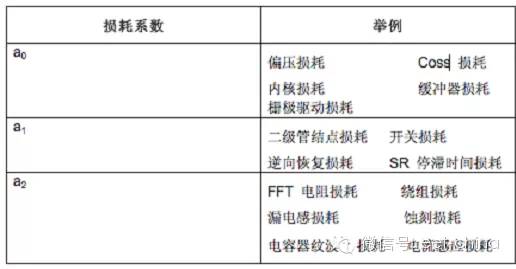
代數式下一位將最佳電流代回到效率方程式中,解得最大效率為:
需要最小化該表達式中的最后兩項,以最佳化效率。a1 項很簡單,只需對其最小化即可。末尾項能夠實現部分優化。如果假設 MOSFET 的 Coss 和柵極驅動功率與其面積相關,同時其導通電阻與面積成反比,則可以為它選擇最佳面積(和電阻)。圖12.1顯示了裸片面積的優化結果。裸片面積較小時,MOSFET的導通電阻變為效率限制器。隨著裸片面積增加,驅動和Coss損耗也隨之增加,

圖12.1 調節 MOSFET 裸片面積來最小化滿負載功率損耗
圖12.2是圍繞圖12.1最佳點的三種可能設計效率圖。圖中分別顯示了三種設計的正常裸片面積。輕負載情況下,較大面積裸片的效率會受不斷增加的驅動損耗影響,而在重負載條件下小尺寸器件因高傳導損耗而變得不堪重負。這些曲線代表裸片面積和成本的三比一變化,注意這一點非常重要。正常芯片面積設計的效率只比滿功率大面積設計的效率稍低一點,而在輕載條件下(設計常常運行在這種負載條件下)則更高。
圖 12.2 效率峰值出現在滿額定電流之前
責任編輯:lq
-
電源
+關注
關注
184文章
17835瀏覽量
251322 -
開關電源
+關注
關注
6469文章
8368瀏覽量
483135 -
電感
+關注
關注
54文章
6153瀏覽量
102599
原文標題:1w字干貨!開關電源設計超實用技巧
文章出處:【微信號:dianyuankaifa,微信公眾號:電源研發精英圈】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
教你如何正確選擇貼片電容的容量
電源濾波器對電源頻率的衰減程度是怎樣的?
如何正確選擇適用的貼片電感?





 為電源選擇正確的工作頻率
為電源選擇正確的工作頻率












評論