今天我們來了解一番電容中絕緣介質的相對介電常數,可能有的小伙伴就要問了:“電容器生產出來之后,介質都固定了,我們了解電容介質的介電常數的影響又有什么作用呢?”請大家稍安勿躁,且聽我慢慢道來。作為攻城獅不僅僅需要關注實際電容器,更需要關注信號傳輸路徑中的電容。例如信號線對地平面構成的電容大小會直接影響傳輸線阻抗、信號線對周圍信號線的電容大小會直接影響串擾等。
在影響電容量的3個主要因素中,極板面積和極板間距是很直觀的。然而相對介電常數看似是固定的材料屬性,但在實際場景中就比較復雜了。舉個栗子:同一塊使用FR4做為介質的PCB,內層的帶狀線上下兩端介質的相對介電常數都是4,信號線感受到的相對介電常數就是材料的相對介電常數(4)。那表層的微帶線呢?一面是相對介電常數是1的空氣,一面是相對介電常數是4的FR4。那么表層微帶線感受的有效介電常數是多少呢?這里先容我賣個關子。
首先我們得知道什么是相對介電常數:介電常數是導體間的絕緣材料增加它們之間電容量的特性。而相對介電常數就是導體被絕緣材料包圍時的電容量與導體被空氣包圍時的電容量的比值。
相對介電常數公式如下。
當導體周圍填充的是均勻介質時,導體感受到的介電常數是介質的相對介電常數,如果周圍填充的是非均勻介質的時候,那么導體感受到的介電常數和兩種介質的相對介電常數有關。這時電力線通過不同介電常數的介質材料時所感受到的介電常數就稱為有效介電常數。
這次我們就不舉栗子了,今天舉大米……
以一塊水稻田為例,當稻田不施肥(介質是空氣),秋天能收獲稻谷200斤(使用空氣做介質的電容量),當使用化肥A(介質是FR4),秋天能收獲稻谷800斤(使用FR4做介質的電容量)。 那么化肥A的增產常數(相對介電常數)是施肥產量和不施肥產量的比值,即 800斤/200斤=4。這樣大家是不是都明白了相對介電常數是怎么來的?使用一種化肥,田的實際增產常數等于化肥的相對增產常數。
那假如這塊田一部分不施肥(介質是空氣),一部分使用化肥A(介質是FR4),那么怎么計算這塊田實際增產常數(有效介電常數)呢?計算方法如下公式。
通常有效介電常數的精確數值需要用仿真器模擬才能得出,下面提供一種使用阻抗計算軟件擬合微帶線感受到的有效介電常數的方法:
PCB表層的微帶線,電力線會穿過空氣和FR4,感受到的介電常數會不同。由于介電常數會影響電容的增幅,所以介電常數的波動也直接影響電容量。因為電感則不受介質屬性影響,所以介電常數的波動的變化會直接導致阻抗的變化,根據阻抗公式
可以通過下面的方法來得到。
1:使用非嵌入式微帶線模型,一面接觸空氣,一面接觸FR4時的線路阻抗(猜想:此微帶線模型內部算法是考慮了空氣的,因為空氣的參數固定所以沒有設置選項)。
2:使用嵌入式微帶線模型,用H2模擬空氣,介電常數為1,厚度盡量大,盡量包裹所有的電力線。猜想用嵌入式微帶線的H2模擬空氣參數得到的阻抗與非嵌入式微帶線獲得的阻抗一致。
根據軟件計算的結果,兩組模型獲得的結果非常接近,證實了猜想,非嵌入微帶線模型是考慮了空氣影響的,實際上是一種特殊的嵌入式微帶線。
3:在驗證了非嵌入式微帶線模型實際是一種特殊的嵌入式微帶線后,我們用嵌入式微帶線模型進行有效介電常數的擬合。
根據擬合結果:微帶線一面接觸空氣,一面接觸FR4時,銅厚厚度1.2MIL,如將空氣和FR4看成一個整體(一塊田),走線感受到的有效相對介電常數約是2.9(實際增產常數)。此方法獲得的擬合結果是近似值,帶狀線也可以用相同方式擬合。
了解了相對介電常數對電容的影響,以及多種不同相對介電常數介質對電容的影響,有助于分析因介電常數變化引起的反射、串擾、延時等問題。其中典型就是板材的玻纖效應:PCB常用介質FR4是玻璃纖維布與環氧樹脂混合成的,電力線穿過這兩種介電常數不同的介質,感受到的有效介電常數就是FR4的相對介電常數。而常用的1080、106等型號的玻璃布是網格狀,網格內和網格外的玻璃纖維布與環氧樹脂的比例不同,且玻璃纖維布的相對介電常數高于環氧樹脂的相對介電常數,導致網格內和網格外的有效介電常數不同。所以走在網格內的信號線比走在網格外的信號線感受的有效介電常數更低;同時走在網格中的信號比玻纖布上的信號更快到達,兩信號線雖然等長但是并不等時。有效介電常數直接影響電容量,進而影響阻抗,阻抗的突變將引起反射,這就是我們常說的玻纖效應。
編輯:hfy
-
電容器
+關注
關注
64文章
6253瀏覽量
100057 -
pcb
+關注
關注
4324文章
23159瀏覽量
399307 -
信號線
+關注
關注
2文章
176瀏覽量
21532 -
信號傳輸
+關注
關注
4文章
437瀏覽量
20248
發布評論請先 登錄
相關推薦
介電常數定義是什么_介電常數單位是什么
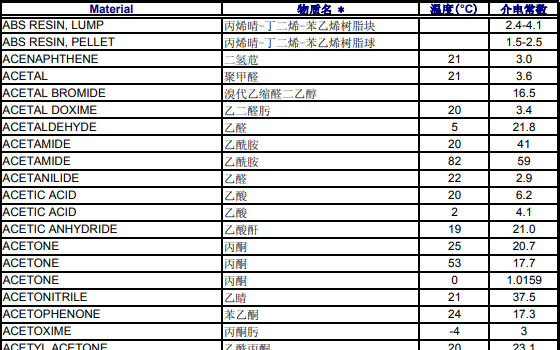
各種材料的相對介電常數詳細參考表免費下載
什么是相對介電常數?介電常數對電容的影響資料下載





 淺談電容中絕緣介質的相對介電常數
淺談電容中絕緣介質的相對介電常數
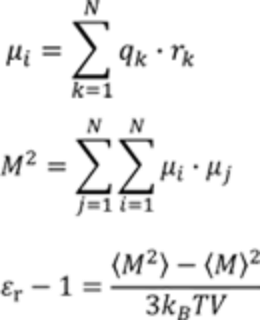










評論