本文介紹了基礎統計分布的重要特征,并說明了概率密度函數的重要性。
本文是我們關于電氣工程統計的系列文章的續篇。前兩篇文章討論了統計分析和統計性描述,為我們的討論奠定了基礎。
然后,我們研究了信號處理中的平均偏差,標準偏差和方差-在計算標準偏差時要特別注意樣本量補償。在上一篇文章中,我們通過探索標準差與均方根值的關系來進一步推斷我們對標準差的理解。在本文中,我們將介紹正態分布在電氣工程中的位置,特別是在評估概率密度函數中。
什么是正態分布?
如果您反復測量一個或多或少隨機變化的量(噪聲信號中的電壓電平,47kΩ電阻器的實際電阻值,工程等級的測試分數,草坪上的草葉長度等),隨著越來越多的數據積累,值的分布可能會逐漸類似于以下所示的形狀。
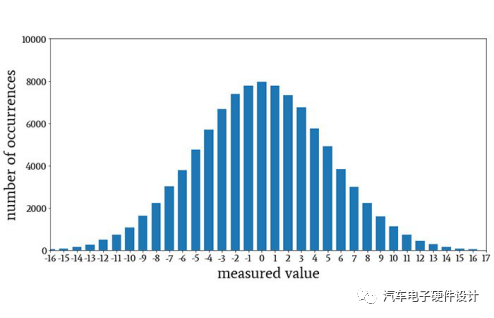
表示正態分布或高斯分布的直方圖。
這稱為正態分布或高斯分布。它遵循熟悉的鐘形曲線形狀,但是使用名稱“正態”或“高斯”而不是“鐘形曲線”非常重要,因為其他類型的分布具有相似的形狀。在進行統計分析時,在工程,物理科學和社會科學領域研究的大量現象將產生正態分布。
正態分布的特征
正態分布是一種數學上定義的關系,用于描述數據集中的值,而現實生活中的測量值隨著樣本量的增加而近似于這種關系。讓我們看一下正態分布的一些重要特征。
給定正態分布的特定形狀完全由均值和標準偏差定義。換句話說,如果您知道正態分布數據集的平均值和標準偏差,則可以繪制直方圖的形狀。
平均值確定曲線中心的位置,標準偏差確定其表觀寬度。在上面顯示的分布中,平均值為0,標準偏差為5。
盡管從理論上講,高斯曲線延伸到正和負無窮大,但是當值在均值之上或之下大于約3個標準偏差時,預期的出現次數將變得非常小。
直方圖和概率密度函數
如果我們為遵循正態分布的變量收集了大量數據,則可以將這些數據顯示為直方圖,并且將具有高斯曲線形狀。另一方面,如果我們知道數據的均值和標準差,則可以畫出與我們的經驗觀察值相對應的概率密度函數。
為此,我們使用以下公式:
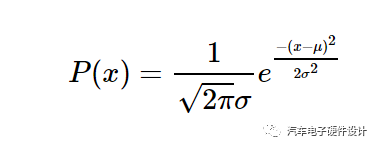
其中,μ是平均值,σ是標準偏差。
這是平均值為0,標準偏差為5的正態分布變量的概率密度函數圖。
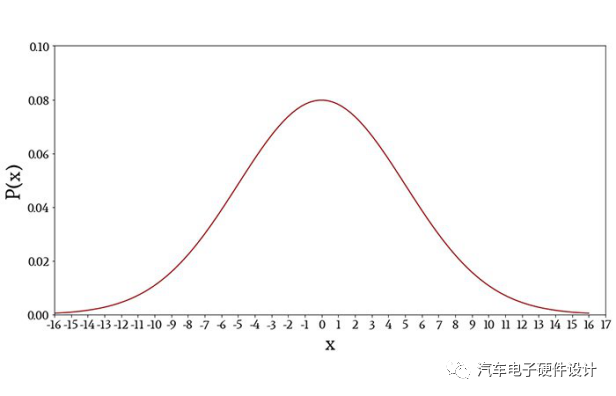
正態分布變量的圖密度函數。在這種情況下,平均值為0,標準偏差為5。解釋概率密度函數
通過計算給定間隔(例如,從–3到+3)內P(x)曲線下的面積,我們可以確定隨機選擇的測量值落入該間隔的概率。出于實際目的,我們也可以將P(x)解釋為隨機選擇的測量將近似等于某個值的可能性。
例如,假設上面顯示的概率密度函數對應于我們通過測量傳感器信號的電壓(以毫伏為單位)生成的直方圖。所有值均四舍五入至最接近的毫伏。平均值為0 V,標準偏差為5 mV。
我們使用上面給出的公式計算了高斯P(x),并繪制了P(x)來繪制一條曲線,該曲線是所測傳感器電壓分布的連續數學表示。現在,我們查看該圖,發現6 mV的值對應于P(x)= 0.04,這表明隨機選擇的電壓測量值大約為6 mV的可能性為4%。
我發現以這種方式考慮概率密度函數很有幫助,但是請記住,從嚴格的數學角度來看,這種解釋是不正確的。概率密度函數是連續的,因此,概率僅在一個時間間隔內為非零值,而不是沿水平軸的一個精確值。
概率密度函數的歸一化
所有概率密度函數都經過歸一化,因此曲線下的總面積為1。
這是有道理的:整條曲線下方的區域為我們提供了隨機選擇的測量值落入與整條曲線相對應的間隔內的可能性。由于該值有100%的機會會在此間隔內某個位置,因此積分P(x)的結果必須為1。
由于這種歸一化,如果我們在同一軸上繪制P(x)和直方圖,它們將不會重合:P(x)在垂直軸上僅從0擴展到0.08,而直方圖從0擴展到8000(因為它是使用100,000個數據點生成的)。
但是,如果我將P(x)乘以100,000,并將結果曲線包括在直方圖中,您會發現高斯概率密度函數可以數學方式捕獲所測得的分布。
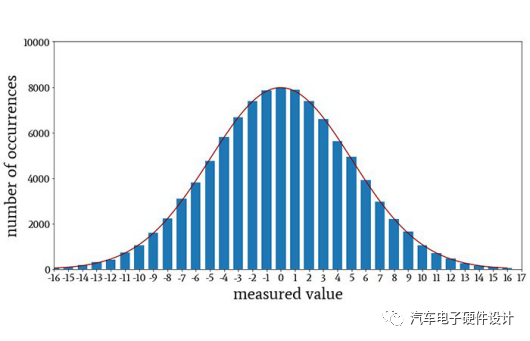
當我們將P(x)乘以100,000并將結果曲線包括在直方圖中時,高斯概率密度函數。結論
我希望您喜歡這篇文章,并希望它介紹了正態分布并在實踐和理論上取得了很好的平衡。在下一篇文章中,我們將繼續討論正態分布。
責任編輯:lq
-
電阻器
+關注
關注
21文章
3796瀏覽量
62249 -
函數
+關注
關注
3文章
4345瀏覽量
62870 -
電氣工程
+關注
關注
5文章
99瀏覽量
17638
原文標題:電氣工程正態分布簡介
文章出處:【微信號:QCDZYJ,微信公眾號:汽車電子工程知識體系】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
銅排在電氣工程中的應用
thd在電氣工程中的作用
在實際的電氣連接中,是直接將Exposed Thermal Pad連接到AGND嗎?
圖像高斯濾波的原理及FPGA實現思路

電位器的電氣特性分析 電位器在音頻設備中的應用
智芯公司亮相2024第二屆中國電氣工程大會
頻譜分析儀在音頻工程中的應用
電氣工程師最喜歡用的編程方法
【探討】DTAS尺寸公差分析與尺寸鏈計算邀您探索單孔銷浮動之奧秘(二),快來圍觀吧!
分布式智慧終端在水利工程建設中的實時監控解決方案
分布式系統在交通監控工程中的創新應用案例
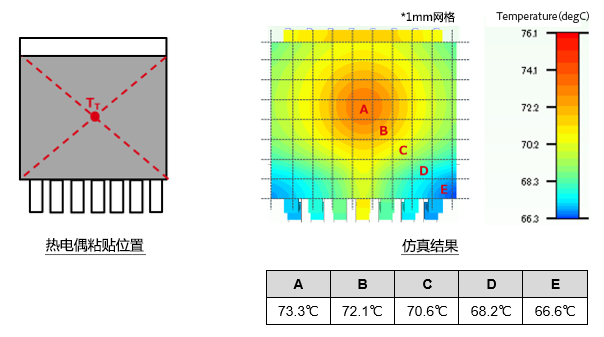
熱電偶的安裝位置介紹




 介紹正態分布在電氣工程中的位置
介紹正態分布在電氣工程中的位置












評論