在強(qiáng)化學(xué)習(xí)(五)用時(shí)序差分法(TD)求解中,我們討論了用時(shí)序差分來(lái)求解強(qiáng)化學(xué)習(xí)預(yù)測(cè)問(wèn)題的方法,但是對(duì)控制算法的求解過(guò)程沒(méi)有深入,本文我們就對(duì)時(shí)序差分的在線控制算法SARSA做詳細(xì)的討論。
SARSA這一篇對(duì)應(yīng)Sutton書(shū)的第六章部分和UCL強(qiáng)化學(xué)習(xí)課程的第五講部分。
1.SARSA算法的引入
SARSA算法是一種使用時(shí)序差分求解強(qiáng)化學(xué)習(xí)控制問(wèn)題的方法,回顧下此時(shí)我們的控制問(wèn)題可以表示為:給定強(qiáng)化學(xué)習(xí)的5個(gè)要素:狀態(tài)集SS, 動(dòng)作集AA, 即時(shí)獎(jiǎng)勵(lì)RR,衰減因子γγ, 探索率??, 求解最優(yōu)的動(dòng)作價(jià)值函數(shù)q?q?和最優(yōu)策略π?π?。
這一類(lèi)強(qiáng)化學(xué)習(xí)的問(wèn)題求解不需要環(huán)境的狀態(tài)轉(zhuǎn)化模型,是不基于模型的強(qiáng)化學(xué)習(xí)問(wèn)題求解方法。對(duì)于它的控制問(wèn)題求解,和蒙特卡羅法類(lèi)似,都是價(jià)值迭代,即通過(guò)價(jià)值函數(shù)的更新,來(lái)更新當(dāng)前的策略,再通過(guò)新的策略,來(lái)產(chǎn)生新的狀態(tài)和即時(shí)獎(jiǎng)勵(lì),進(jìn)而更新價(jià)值函數(shù)。一直進(jìn)行下去,直到價(jià)值函數(shù)和策略都收斂。
再回顧下時(shí)序差分法的控制問(wèn)題,可以分為兩類(lèi),一類(lèi)是在線控制,即一直使用一個(gè)策略來(lái)更新價(jià)值函數(shù)和選擇新的動(dòng)作。而另一類(lèi)是離線控制,會(huì)使用兩個(gè)控制策略,一個(gè)策略用于選擇新的動(dòng)作,另一個(gè)策略用于更新價(jià)值函數(shù)。
我們的SARSA算法,屬于在線控制這一類(lèi),即一直使用一個(gè)策略來(lái)更新價(jià)值函數(shù)和選擇新的動(dòng)作,而這個(gè)策略是????貪婪法,在強(qiáng)化學(xué)習(xí)(四)用蒙特卡羅法(MC)求解中,我們對(duì)于????貪婪法有詳細(xì)講解,即通過(guò)設(shè)置一個(gè)較小的??值,使用1??1??的概率貪婪地選擇目前認(rèn)為是最大行為價(jià)值的行為,而用??的概率隨機(jī)的從所有m個(gè)可選行為中選擇行為。用公式可以表示為:
π(a|s)={?/m+1???/mifa?=argmaxa∈AQ(s,a)elseπ(a|s)={?/m+1??ifa?=arg?maxa∈AQ(s,a)?/melse
2. SARSA算法概述
作為SARSA算法的名字本身來(lái)說(shuō),它實(shí)際上是由S,A,R,S,A幾個(gè)字母組成的。而S,A,R分別代表狀態(tài)(State),動(dòng)作(Action),獎(jiǎng)勵(lì)(Reward),這也是我們前面一直在使用的符號(hào)。這個(gè)流程體現(xiàn)在下圖:
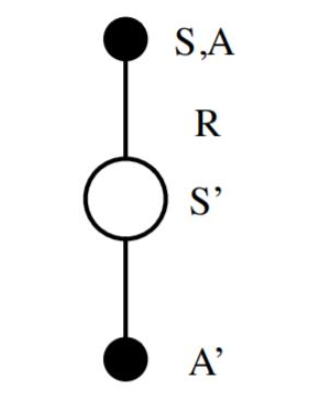
在迭代的時(shí)候,我們首先基于????貪婪法在當(dāng)前狀態(tài)SS選擇一個(gè)動(dòng)作AA,這樣系統(tǒng)會(huì)轉(zhuǎn)到一個(gè)新的狀態(tài)S′S′, 同時(shí)給我們一個(gè)即時(shí)獎(jiǎng)勵(lì)RR, 在新的狀態(tài)S′S′,我們會(huì)基于????貪婪法在狀態(tài)S‘′S‘′選擇一個(gè)動(dòng)作A′A′,但是注意這時(shí)候我們并不執(zhí)行這個(gè)動(dòng)作A′A′,只是用來(lái)更新的我們的價(jià)值函數(shù),價(jià)值函數(shù)的更新公式是:
Q(S,A)=Q(S,A)+α(R+γQ(S′,A′)?Q(S,A))Q(S,A)=Q(S,A)+α(R+γQ(S′,A′)?Q(S,A))
其中,γγ是衰減因子,αα是迭代步長(zhǎng)。這里和蒙特卡羅法求解在線控制問(wèn)題的迭代公式的區(qū)別主要是,收獲GtGt的表達(dá)式不同,對(duì)于時(shí)序差分,收獲GtGt的表達(dá)式是R+γQ(S′,A′)R+γQ(S′,A′)。這個(gè)價(jià)值函數(shù)更新的貝爾曼公式我們?cè)趶?qiáng)化學(xué)習(xí)(五)用時(shí)序差分法(TD)求解第2節(jié)有詳細(xì)講到。
除了收獲GtGt的表達(dá)式不同,SARSA算法和蒙特卡羅在線控制算法基本類(lèi)似。
3. SARSA算法流程
下面我們總結(jié)下SARSA算法的流程。
算法輸入:迭代輪數(shù)TT,狀態(tài)集SS, 動(dòng)作集AA, 步長(zhǎng)αα,衰減因子γγ, 探索率??,
輸出:所有的狀態(tài)和動(dòng)作對(duì)應(yīng)的價(jià)值QQ
1. 隨機(jī)初始化所有的狀態(tài)和動(dòng)作對(duì)應(yīng)的價(jià)值QQ. 對(duì)于終止?fàn)顟B(tài)其QQ值初始化為0.
2. for i from 1 to T,進(jìn)行迭代。
a) 初始化S為當(dāng)前狀態(tài)序列的第一個(gè)狀態(tài)。設(shè)置AA為????貪婪法在當(dāng)前狀態(tài)SS選擇的動(dòng)作。
b) 在狀態(tài)SS執(zhí)行當(dāng)前動(dòng)作AA,得到新?tīng)顟B(tài)S′S′和獎(jiǎng)勵(lì)RR
c) 用????貪婪法在狀態(tài)S′S′選擇新的動(dòng)作A′A′
d) 更新價(jià)值函數(shù)Q(S,A)Q(S,A):
Q(S,A)=Q(S,A)+α(R+γQ(S′,A′)?Q(S,A))Q(S,A)=Q(S,A)+α(R+γQ(S′,A′)?Q(S,A))
e)S=S′,A=A′S=S′,A=A′
f) 如果S′S′是終止?fàn)顟B(tài),當(dāng)前輪迭代完畢,否則轉(zhuǎn)到步驟b)
這里有一個(gè)要注意的是,步長(zhǎng)αα一般需要隨著迭代的進(jìn)行逐漸變小,這樣才能保證動(dòng)作價(jià)值函數(shù)QQ可以收斂。當(dāng)QQ收斂時(shí),我們的策略????貪婪法也就收斂了。
4. SARSA算法實(shí)例:Windy GridWorld
下面我們用一個(gè)著名的實(shí)例Windy GridWorld來(lái)研究SARSA算法。
如下圖一個(gè)10×7的長(zhǎng)方形格子世界,標(biāo)記有一個(gè)起始位置 S 和一個(gè)終止目標(biāo)位置 G,格子下方的數(shù)字表示對(duì)應(yīng)的列中一定強(qiáng)度的風(fēng)。當(dāng)個(gè)體進(jìn)入該列的某個(gè)格子時(shí),會(huì)按圖中箭頭所示的方向自動(dòng)移動(dòng)數(shù)字表示的格數(shù),借此來(lái)模擬世界中風(fēng)的作用。同樣格子世界是有邊界的,個(gè)體任意時(shí)刻只能處在世界內(nèi)部的一個(gè)格子中。個(gè)體并不清楚這個(gè)世界的構(gòu)造以及有風(fēng),也就是說(shuō)它不知道格子是長(zhǎng)方形的,也不知道邊界在哪里,也不知道自己在里面移動(dòng)移步后下一個(gè)格子與之前格子的相對(duì)位置關(guān)系,當(dāng)然它也不清楚起始位置、終止目標(biāo)的具體位置。但是個(gè)體會(huì)記住曾經(jīng)經(jīng)過(guò)的格子,下次在進(jìn)入這個(gè)格子時(shí),它能準(zhǔn)確的辨認(rèn)出這個(gè)格子曾經(jīng)什么時(shí)候來(lái)過(guò)。格子可以執(zhí)行的行為是朝上、下、左、右移動(dòng)一步,每移動(dòng)一步只要不是進(jìn)入目標(biāo)位置都給予一個(gè) -1 的懲罰,直至進(jìn)入目標(biāo)位置后獲得獎(jiǎng)勵(lì) 0 同時(shí)永久停留在該位置。現(xiàn)在要求解的問(wèn)題是個(gè)體應(yīng)該遵循怎樣的策略才能盡快的從起始位置到達(dá)目標(biāo)位置。
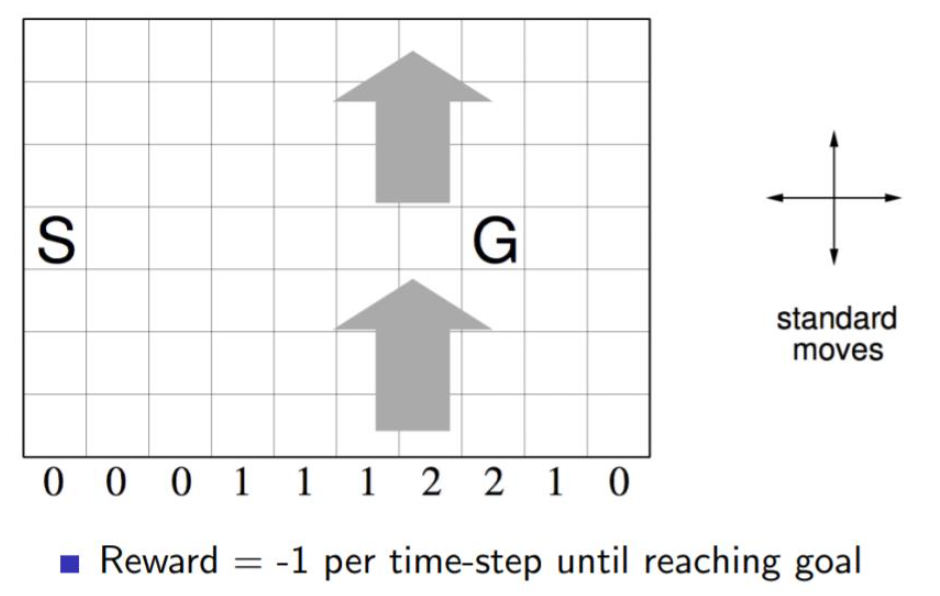
邏輯并不復(fù)雜,完整的代碼在我的github。這里我主要看一下關(guān)鍵部分的代碼。
算法中第2步步驟a,初始化SS,使用????貪婪法在當(dāng)前狀態(tài)SS選擇的動(dòng)作的過(guò)程:
# initialize state
state = START
# choose an action based on epsilon-greedy algorithm
if np.random.binomial(1, EPSILON) == 1:
action = np.random.choice(ACTIONS)
else:
values_ = q_value[state[0], state[1], :]
action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
算法中第2步步驟b,在狀態(tài)SS執(zhí)行當(dāng)前動(dòng)作AA,得到新?tīng)顟B(tài)S′S′的過(guò)程,由于獎(jiǎng)勵(lì)不是終止就是-1,不需要單獨(dú)計(jì)算:
def step(state, action):
i, j = state
if action == ACTION_UP:
return [max(i - 1 - WIND[j], 0), j]
elif action == ACTION_DOWN:
return [max(min(i + 1 - WIND[j], WORLD_HEIGHT - 1), 0), j]
elif action == ACTION_LEFT:
return [max(i - WIND[j], 0), max(j - 1, 0)]
elif action == ACTION_RIGHT:
return [max(i - WIND[j], 0), min(j + 1, WORLD_WIDTH - 1)]
else:
assert False
算法中第2步步驟c,用????貪婪法在狀態(tài)S‘S‘選擇新的動(dòng)作A′A′的過(guò)程:
next_state = step(state, action)
if np.random.binomial(1, EPSILON) == 1:
next_action = np.random.choice(ACTIONS)
else:
values_ = q_value[next_state[0], next_state[1], :]
next_action = np.random.choice([action_ for action_, value_ in enumerate(values_) if value_ == np.max(values_)])
算法中第2步步驟d,e,更新價(jià)值函數(shù)Q(S,A)Q(S,A)以及更新當(dāng)前狀態(tài)動(dòng)作的過(guò)程:
# Sarsa update
q_value[state[0], state[1], action] += \
ALPHA * (REWARD + q_value[next_state[0], next_state[1], next_action] -
q_value[state[0], state[1], action])
state = next_state
action = next_action
代碼很簡(jiǎn)單,相信大家對(duì)照算法,跑跑代碼,可以很容易得到這個(gè)問(wèn)題的最優(yōu)解,進(jìn)而搞清楚SARSA算法的整個(gè)流程。
5. SARSA(λλ)
在強(qiáng)化學(xué)習(xí)(五)用時(shí)序差分法(TD)求解中我們講到了多步時(shí)序差分TD(λ)TD(λ)的價(jià)值函數(shù)迭代方法,那么同樣的,對(duì)應(yīng)的多步時(shí)序差分在線控制算法,就是我們的SARSA(λ)SARSA(λ)。
TD(λ)TD(λ)有前向和后向兩種價(jià)值函數(shù)迭代方式,當(dāng)然它們是等價(jià)的。在控制問(wèn)題的求解時(shí),基于反向認(rèn)識(shí)的SARSA(λ)SARSA(λ)算法將可以有效地在線學(xué)習(xí),數(shù)據(jù)學(xué)習(xí)完即可丟棄。因此SARSA(λ)SARSA(λ)算法默認(rèn)都是基于反向來(lái)進(jìn)行價(jià)值函數(shù)迭代。
在上一篇我們講到了TD(λ)TD(λ)狀態(tài)價(jià)值函數(shù)的反向迭代,即:
δt=Rt+1+γV(St+1)?V(St)δt=Rt+1+γV(St+1)?V(St)
V(St)=V(St)+αδtEt(S)V(St)=V(St)+αδtEt(S)
對(duì)應(yīng)的動(dòng)作價(jià)值函數(shù)的迭代公式可以找樣寫(xiě)出,即:
δt=Rt+1+γQ(St+1,At+1)?Q(St,At)δt=Rt+1+γQ(St+1,At+1)?Q(St,At)
Q(St,At)=Q(St,At)+αδtEt(S,A)Q(St,At)=Q(St,At)+αδtEt(S,A)
除了狀態(tài)價(jià)值函數(shù)Q(S,A)Q(S,A)的更新方式,多步參數(shù)λλ以及反向認(rèn)識(shí)引入的效用跡E(S,A)E(S,A),其余算法思想和SARSA類(lèi)似。這里我們總結(jié)下SARSA(λ)SARSA(λ)的算法流程。
算法輸入:迭代輪數(shù)TT,狀態(tài)集SS, 動(dòng)作集AA, 步長(zhǎng)αα,衰減因子γγ, 探索率??,多步參數(shù)λλ
輸出:所有的狀態(tài)和動(dòng)作對(duì)應(yīng)的價(jià)值QQ
1. 隨機(jī)初始化所有的狀態(tài)和動(dòng)作對(duì)應(yīng)的價(jià)值QQ. 對(duì)于終止?fàn)顟B(tài)其QQ值初始化為0.
2. for i from 1 to T,進(jìn)行迭代。
a) 初始化所有狀態(tài)動(dòng)作的效用跡EE為0,初始化S為當(dāng)前狀態(tài)序列的第一個(gè)狀態(tài)。設(shè)置AA為????貪婪法在當(dāng)前狀態(tài)SS選擇的動(dòng)作。
b) 在狀態(tài)SS執(zhí)行當(dāng)前動(dòng)作AA,得到新?tīng)顟B(tài)S′S′和獎(jiǎng)勵(lì)RR
c) 用????貪婪法在狀態(tài)S′S′選擇新的動(dòng)作A′A′
d) 更新效用跡函數(shù)E(S,A)E(S,A)和TD誤差δδ:
E(S,A)=E(S,A)+1E(S,A)=E(S,A)+1
δ=Rt+1+γQ(St+1,At+1)?Q(St,At)δ=Rt+1+γQ(St+1,At+1)?Q(St,At)
e) 對(duì)當(dāng)前序列所有出現(xiàn)的狀態(tài)s和對(duì)應(yīng)動(dòng)作a, 更新價(jià)值函數(shù)Q(s,a)Q(s,a)和效用跡函數(shù)E(s,a)E(s,a):
Q(s,a)=Q(s,a)+αδE(s,a)Q(s,a)=Q(s,a)+αδE(s,a)
E(s,a)=γλE(s,a)E(s,a)=γλE(s,a)
f)S=S′,A=A′S=S′,A=A′
g) 如果S′S′是終止?fàn)顟B(tài),當(dāng)前輪迭代完畢,否則轉(zhuǎn)到步驟b)
對(duì)于步長(zhǎng)αα,和SARSA一樣,一般也需要隨著迭代的進(jìn)行逐漸變小才能保證動(dòng)作價(jià)值函數(shù)QQ收斂。
6. SARSA小結(jié)
SARSA算法和動(dòng)態(tài)規(guī)劃法比起來(lái),不需要環(huán)境的狀態(tài)轉(zhuǎn)換模型,和蒙特卡羅法比起來(lái),不需要完整的狀態(tài)序列,因此比較靈活。在傳統(tǒng)的強(qiáng)化學(xué)習(xí)方法中使用比較廣泛。
但是SARSA算法也有一個(gè)傳統(tǒng)強(qiáng)化學(xué)習(xí)方法共有的問(wèn)題,就是無(wú)法求解太復(fù)雜的問(wèn)題。在 SARSA 算法中,Q(S,A)Q(S,A)的值使用一張大表來(lái)存儲(chǔ)的,如果我們的狀態(tài)和動(dòng)作都達(dá)到百萬(wàn)乃至千萬(wàn)級(jí),需要在內(nèi)存里保存的這張大表會(huì)超級(jí)大,甚至溢出,因此不是很適合解決規(guī)模很大的問(wèn)題。當(dāng)然,對(duì)于不是特別復(fù)雜的問(wèn)題,使用SARSA還是很不錯(cuò)的一種強(qiáng)化學(xué)習(xí)問(wèn)題求解方法。
-
算法
+關(guān)注
關(guān)注
23文章
4629瀏覽量
93193 -
控制算法
+關(guān)注
關(guān)注
4文章
166瀏覽量
21761 -
SARSA
+關(guān)注
關(guān)注
0文章
2瀏覽量
1329
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
基于差分演化算法的PID參數(shù)優(yōu)化算法
對(duì)Rijndael的JAVA差分攻擊與防范
SHACAL-2算法的差分故障攻擊
修正的強(qiáng)跟蹤有限差分濾波算法
基于差分隱私的軌跡模式挖掘算法

基于鄰域差分和協(xié)方差信息處理單目標(biāo)優(yōu)化的進(jìn)化算法
基于雙變異策略的骨架差分算法
面向隨機(jī)森林的差分隱私保護(hù)算法
如何使用差分隱私保護(hù)進(jìn)行譜聚類(lèi)算法
淺談Q-Learning和SARSA時(shí)序差分算法
強(qiáng)化學(xué)習(xí)的雙權(quán)重最小二乘Sarsa算法

基于北斗衛(wèi)星差分定位法的導(dǎo)線舞動(dòng)在線監(jiān)測(cè)-風(fēng)河智能

淺談煤礦企業(yè)能耗在線監(jiān)測(cè)系統(tǒng)的設(shè)計(jì)與應(yīng)用




 淺談時(shí)序差分的在線控制算法—SARSA
淺談時(shí)序差分的在線控制算法—SARSA











評(píng)論