引言
神經網絡中涉及到大量的張量運算,比如卷積,矩陣乘法,向量點乘,求和等。神經網絡加速器就是針對張量運算來設計的。一個神經網絡加速器通常都包含一個張量計算陣列,以及數據收發控制,共同來完成諸如矩陣乘法,卷積等計算任務。運算靈活多變的特性和硬件的固定架構產生了矛盾,這個矛盾造成了利用硬件執行計算任務的算法多變性。不同的硬件架構實現相同的計算,可能具有不同的算法。我們今天討論基于脈動陣列的計算架構,脈動陣列的低延遲,低扇出特性使其得到廣泛應用,比如TPU中。我們今天就從矩陣計算講起,談一談矩陣計算的幾種不同方式,矩陣的一些特性,再講一講CNN中的卷積運算,最后談談這些張量計算在硬件中的實現形式。
矩陣計算
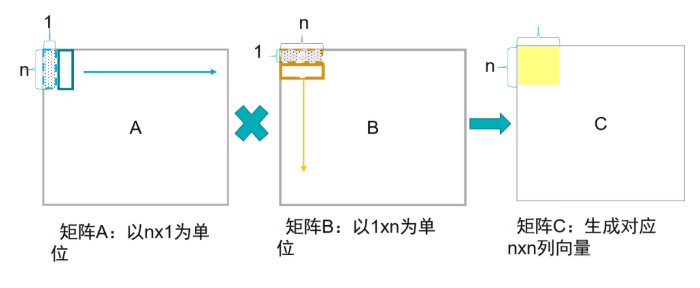
假設有兩個矩陣:
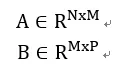
計算這兩個矩陣的乘積
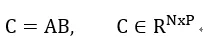
根據矩陣計算形式,我們可以看出有三級循環。根據排列組合,可以有6種計算形式。我們使用ijk分別表示A對應的行,列(B的行),以及B的列的標號。這六種循環計算方式為:ijk, jik, ikj, jki, kij, kji。這六種方式在硬件上(脈動陣列)實現起來,考慮到緩存和計算結構,實際上可以分為2種方式。
1) 矩陣x向量
我們用偽代碼表示為:
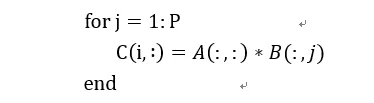
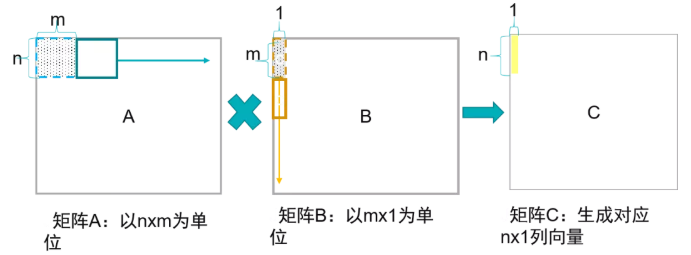
在這種方式下,通過矩陣x向量的方式可以配合脈動陣列的2D結構。這個時候片上要先存儲下一個A矩陣和B矩陣的一列,然后通過一個周期完成矩陣x向量的計算,得到了C矩陣的一行。這個時候片上A矩陣數據可以一直保存不更換,而不斷更換每一列的B數據,直到完成AB計算。
這種方式在在語音處理的LSTM等網絡中比較適用,因為語音通常都是一些連續的向量,而且LSTM網絡決定了連續的向量之間有依賴關系,因此矩陣x向量方式可以提高LSTM中權重的時間復用率。所謂時間復用率是指權重可以在片上保持較長的時間,而不斷更換輸入。從時間維度上看,權重得到了復用。
這種方式的缺點是權重加載到片上會消耗很多時間,突發的load需要占據很大訪問內存帶寬。而且對片上緩存要求容量較高。特別是當緩存較小權重數量較大的時候,就要通過不斷加載權重到片上來滿足計算需求,這可能會降低加速器性能。為了滿足計算的實時性,權重輸出帶寬需要足夠一個矩陣x向量的計算。這對片上帶寬要求也較高。當然這些都能夠通過一定手段來緩解,比如通過多batch來增加權重空間復用率,降低對帶寬需求和片上緩存要求。
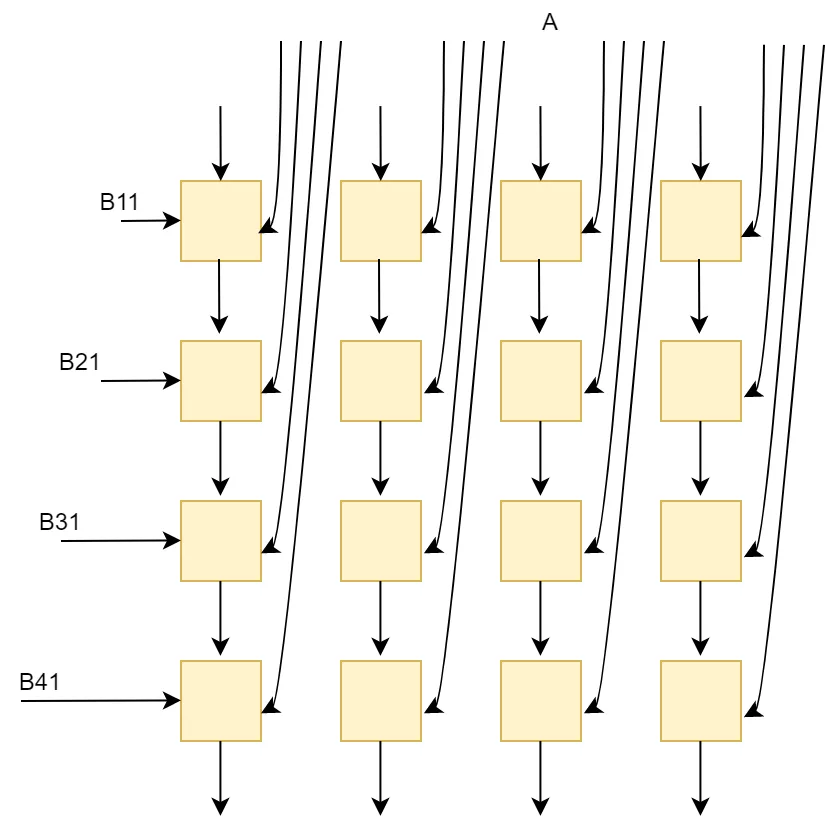
2) 列向量x行向量
用偽代碼表示如下:
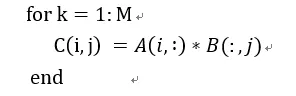
這實際上是取得A的一個列向量和B的行向量進行矩陣乘法,得到一個矩陣,所有對應的A的列和B的行乘積的矩陣和就是最終的C矩陣。這種方式利用了A和B的空間復用率,A的列和B的行的元素彼此求積,也適配了2D的脈動陣列結構。
這種方式對A和B的帶寬需求最低,一般外部DDR的內存可以滿足這樣的要求。對片上緩存需求較低,帶寬也較低。A的列元素和B的行元素分別從脈動陣列的左側和上側進入,相互乘積,達到了元素最大空間復用率。這種方式可能會要求對某個矩陣進行轉置,比如當矩陣按行序列排的時候,B矩陣就需要經過轉置后送入矩陣運算單元進行計算。
但是這種方式也有一定應用限制,對于矩陣x向量的語音識別來說,只有對于batch size較大時,效率才會高,否則會比較低。而且這種結構不太利于脈動陣列在其它方面的應用,比如卷積計算,接下來我們會講到。
塊矩陣計算
硬件上計算陣列通常都是和要進行計算的矩陣大小是不匹配的,一種情況就是計算陣列維度比矩陣維度小,一種就是大于矩陣的維度。
當小于矩陣維度時,可以通過對矩陣切塊來分別計算,如果大于矩陣維度,可以對矩陣進行“補塊”。比如硬件上計算陣列大小是32x32,而A矩陣是64x64,B矩陣是64x64。
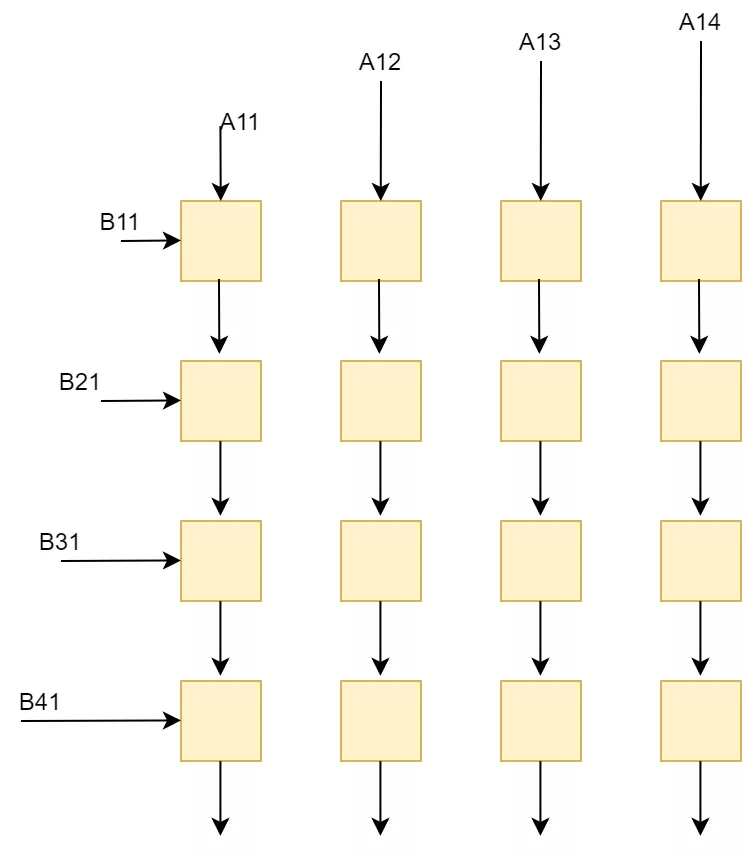
如果采用列向量x行向量的方法,我們就可以將A和B分別切分成4個矩陣快,這些矩陣塊分別進行計算。
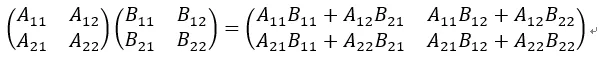
先計算A11xB11(分別將A11按列送入陣列,B11按行輸入陣列,陣列中每個計算單元保留結果繼續和下一次數據求累加和),然后計算A12xB21(繼續不斷將矩陣送入計算陣列,并和上次A11xB11結果求和),兩者求和就得到了第一個矩陣塊。
如果采用矩陣x向量的方法,就可以這樣分塊:

我們先在片上緩存下A1矩陣塊,然后分別加載B1矩陣的列和A1進行矩陣向量計算,分別得到了A1B1矩陣的第一列,第二列,…結果。
矩陣數據表示寬度
硬件上進行神經網絡加速都采用量化后的數據,一般將訓練的模型定點到16bit,8bit,4bit等對硬件計算友好的寬度。因此具有寬bit計算單元的硬件架構可以兼容低bit的神經網絡計算,但是這樣會造成計算資源浪費。所以通常有兩個辦法:一種是針對不同位寬開發不同硬件架構,另外一種是開發出一種同時兼容多種bit的架構。FPGA可重配置的特點,可以在開發階段考慮多種bit計算架構,通過使用參數化定義來為使用者提供架構的可配置選項,客戶可以依據自己需求選擇使用哪種功能。這種方式既滿足了不同bit的計算需求,同時又能夠最大化FPGA資源的使用。
如果我們在低bit架構的基礎上,增加一些其它模塊,也能夠同時兼容寬bit計算任務。這利用到了數據的分解。比如兩個矩陣A和B分別是8bit,我們要用4bit硬件架構加以實現。將A和B按照4bit進行分解:

這個時候看到存在移位和求和,因此硬件中除了4bit計算陣列外,還需要有移位模塊,加法模塊,以及數據位寬轉換模塊。

假設矩陣乘法模塊輸入位寬4bit,輸出32bit可以滿足一般的矩陣大小的乘法,這輸出的32bit數據先通過片上bus緩存到buffer或者給到shift+add模塊,shift+add模塊進行移位求和操作,得到的結果就是正常一個8bit矩陣乘法的結果,這個結果通常在神經網絡中還會被進一步量化,我們假設量化到16bit,那么輸出結果就存放到buffer中。在設計片上buffer的時候,數據單位如果是固定的會使得邏輯簡單,但是現在存在4種數據位寬,所以對buffer中數據的使用就要能靈活處理4bit,8bit,16bit,32bit這樣的大小。這些無疑增加了bufer復雜度。而且shift+add的結構也會增加大量的加法和移位邏輯。
矩陣壓縮
神經網絡種含有的參數很多,大的話都在幾十M甚至上百M。為了在FPGA上能容納更多參數,加速計算任務。通常有兩種方式來對權重進行壓縮:一種是對神經網絡種冗余權重進行剪枝,另外一種是在FPGA上實現對參數壓縮存儲。
剪枝算法有很多,比如針對LSTM的有權重矩陣的稀疏化,設定閾值,去除閾值以下的數據,然后進行fine-tune。這樣得到的矩陣是稀疏矩陣。可以大大減少權重數量。但是這樣的矩陣結構不太利于硬件進行加速,因為它的結構不夠整齊。
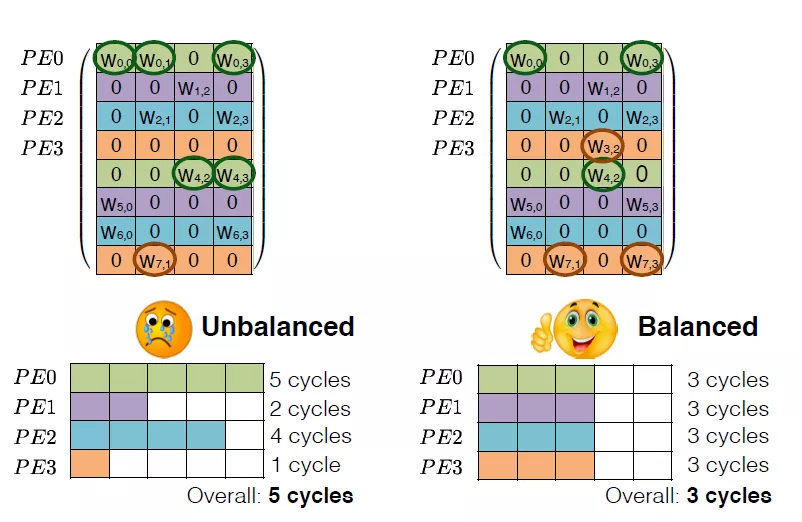
為了得到利于硬件部署的矩陣壓縮結構,可以對權重進行結構化剪枝,即去除一整行或者一整列的數據,保持權重整齊的結構,有利于硬件上進行加速。
Huffman編碼是一種簡潔無損壓縮的熵編碼,簡單來講就是通過統計輸入數據的分布概率,然后重新使用字符來表達原始數據。用最少bit的字符來描述出現概率最大的原始數據,這樣就可以得到一個最優的壓縮比率。編碼可以提前進行,FPGA部分主要是完成解碼。Huffman編碼的壓縮率對于矩陣數據壓縮率很高,唯一的問題是解碼邏輯比較大,解碼效率比較低。這也是很少使用的原因。
卷積
CNN網絡用大量的卷積運算來不斷提取圖像特征,使用了LSTM網絡的語音識別中也有很多包含了卷積處理。CNN中大部分是2D卷積運算,語音識別中很多是1D卷積。通常在每一層卷積神經網絡中含有多個輸入通道和輸出通道,本層輸出通道就是下層的輸入通道。每層的輸入通道都有一個卷積核,這些輸入通道會在卷積之后求和,得到一個輸出通道的結果。
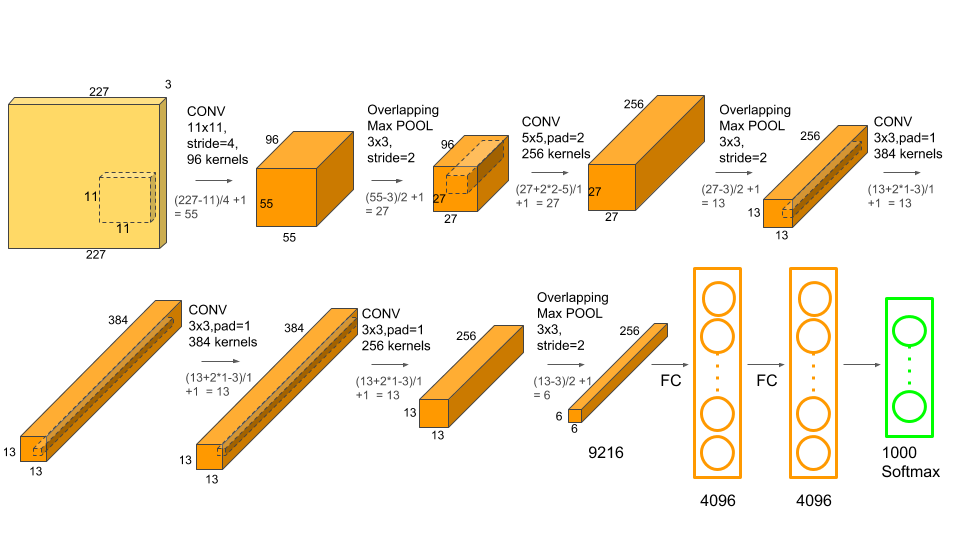
當我們采用脈動陣列來實現卷積的時候,可以有以下幾種方式:
1) 卷積運算->稀疏矩陣乘法
我們以一個1D卷積舉例,假設有個卷積核大小為3x1,輸入向量長度為32。這個卷積用偽代碼表示為:
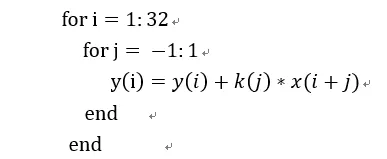
我們將卷積核擴展為一個稀疏矩陣,就可以表達為矩陣向量:

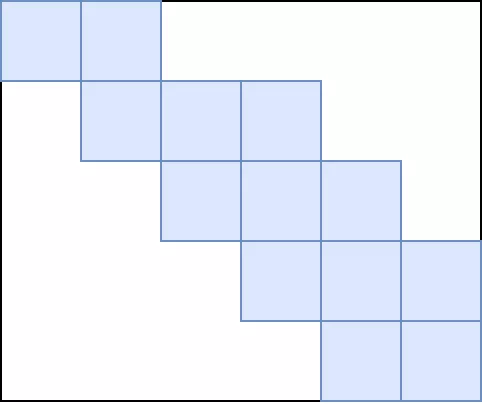
這個卷積矩陣用圖像更清楚:藍色是有效數據,白色是0。用這種方式很簡單的就可以在脈動陣列上進行計算,只需要預先將卷積轉化為矩陣。但是這樣做的缺點就是需要浪費很多存儲空間,同時對計算單元的利用率很低,除非卷積核維度比較大,否則如上卷積核和向量的維度比率,利用率只有3/32。
2) 利用輸入輸出通道,將卷積轉化為矩陣乘法和求和。
我們假設1D卷積核為k,輸入輸出通道分別為i和o。則卷積核表示為:K(o,i)
還假設它是3x1大小。輸入向量是x,假設它長度是32,則某個輸入通道的向量就是:x(i)
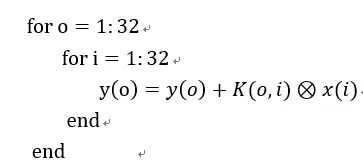
我們看出這個是不是特別像矩陣x向量。如果我們把卷積核分解為三組矩陣,每個矩陣由卷積核對應某個元素在i和o方向拓展得到,那么這樣一個卷積運算就可以被我們轉化為矩陣x向量+矩陣x向量。假設這三組卷積核矩陣是K1(o,i),K2(o,i)和K3(o,i)。同時x按照每個通道的對應元素展開成一個輸入通道i的向量,X1(i), X2(i), …X32(i)。那么我們就可以算出輸出結果是(用第一個y的結果舉例):
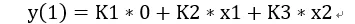
3) 利用脈動陣列結構,改動控制邏輯,直接進行卷積計算。
這個時候需要修改控制邏輯,讓矩陣乘法陣列可以進行卷積計算。其實還可以在i和o的方向將之看作矩陣,但是每個計算單元還存在內部循環讀取卷積核數據。

總結
以上分別總結了矩陣乘法,卷積運算在FPGA加速器上的實現方式。設計一款神經網絡加速器是很多部門的通力合作,算法FPGA編譯器架構,往往一個方案對于某個部門簡單,但是令另外一個部門痛苦。大家在不斷的“拉鋸扯皮”中,一個方案就出來了。
-
FPGA
+關注
關注
1630文章
21759瀏覽量
604370 -
加速器
+關注
關注
2文章
802瀏覽量
37938 -
神經網絡
+關注
關注
42文章
4774瀏覽量
100909 -
張量
+關注
關注
0文章
7瀏覽量
2589
發布評論請先 登錄
相關推薦
人工神經網絡的原理和多種神經網絡架構方法




 張量計算在神經網絡加速器中的實現形式
張量計算在神經網絡加速器中的實現形式










評論