你玩過魔方嗎?
小小的正方體上布滿六種不同的顏色,看似旋轉(zhuǎn)翻飛眼花繚亂,卻總會在某個瞬間完成驚喜變身。魔方作為一種益智玩具,不僅老少皆宜,更是風靡全球,實力堪稱指尖上的藝術(shù)。
但你知道嗎?現(xiàn)在不僅人類在玩,連AI機器人也加入了這個游戲陣營。
看似簡單的小小魔方,你知道它的顏色組合有多少種嗎?
4325 億億種
無論什么樣的顏色組合,最少需要多少次才能保證他們都能復原?
20次
大家可能也聽說,玩得好的人都知道魔方的還原口訣(類似獨孤九劍的口訣)。據(jù)數(shù)學大神們說,世間所有的事物背后都有相應(yīng)的數(shù)學方程去表示或者控制,何況游戲!
其實,魔方所涉及的基本數(shù)學理論就是組合最優(yōu)化。今天,我就給大家分享一下組合最優(yōu)化的基本知識及工程應(yīng)用。
01
什么是組合最優(yōu)化?
通俗地講,組合最優(yōu)化研究的問題就是討論在眾多的組合方案中,什么樣的方案最優(yōu)以及如何找出最優(yōu)方案;
學術(shù)地講,組合最優(yōu)化是一個重要的數(shù)學分支,即通過對數(shù)學方法的研究去尋找事件的最優(yōu)編排,分組,次序或篩選等,其一般數(shù)學模型是:

其中f(X)是目標函數(shù),g(X)是約束函數(shù),D是定義域。
02
抽象數(shù)學表達式具體化
組合最優(yōu)化領(lǐng)域有很多經(jīng)典的例子,它們通俗易懂,很適合鍛煉人的數(shù)學思維能力,好多奧數(shù)競賽的題目就來源于他們。
比如說“旅行商問題”:一個商品推銷員要去若干個(n)城市推銷商品,該推銷員從一個城市出發(fā),需要經(jīng)過所有城市后,回到出發(fā)地,應(yīng)如何選擇行進路線,才能使總的行程最短。初看起來很簡單,窮舉所有可能性的路線,選擇最短的那個,對于n很小的情況,小朋友都能夠理解,也很容易;但對于n比較大的情況,窮舉遍歷法就不可行了。
這是一個普通人都能秒懂的問題,卻也是至今仍未被完全解決的數(shù)學和計算機界難題。除此之外,還有背包問題,匹配問題,排序問題等等,如果誰能夠想清楚這些問題,那數(shù)學思維能力應(yīng)該是杠杠的。
03
組合最優(yōu)化——AI的引擎
AI是個很熱的話題。一方面,最優(yōu)化可以說是AI的引擎,AI問題幾乎都能轉(zhuǎn)化為求解能量/損失函數(shù)的優(yōu)化問題,AI模型訓練的過程就是以損失函數(shù)最小化為目標,采用梯度下降的方法不斷更新模型參數(shù)的過程;
另外一方面,AI深度學習和強化學習技術(shù)也為求解組合最優(yōu)化問題提供了新思路,即組合最優(yōu)化的序列決策可以由深度學習或強化學習來替代,求解組合最優(yōu)化的經(jīng)典算法可以由強化學習幫助指導算法策略,甚至已經(jīng)有了專為組合最優(yōu)化求解而誕生的神經(jīng)網(wǎng)絡(luò)Pointer Network。
04
掌握組合最優(yōu)化,讓生活和工作乘風破浪
組合最優(yōu)化是一門應(yīng)用廣泛、實用性很強的學科,也是一種可以改善生活、提高工作效率的有力工具。
例如,在理財投資中,如何進行投資組合才可以實現(xiàn)收益最大化;在芯片設(shè)計過程中,一個計算機芯片需要多少層才能使得同一層的線路互不相交;在運輸調(diào)度領(lǐng)域,采用什么樣的列車調(diào)度方案可以最大化整個鐵路系統(tǒng)的運行效率;在城建規(guī)劃中,如何安排工廠、超市、住宅、學校、醫(yī)院等單位的布局,才能有利于城市的平衡發(fā)展;在生產(chǎn)計劃安排中,采用什么樣的方案才可以實現(xiàn)利潤最大化。
大到國家政策,中到企業(yè)戰(zhàn)略,小到個人選擇都或多或少地涉及到組合最優(yōu)化。甚至可以說,我們的生活和工作一直在潛意識地進行著最優(yōu)化組合求解,系統(tǒng)的學習和訓練會讓這個過程更高效便捷。
05
我是一名工程師,在博世有哪些工程項目會用到組合最優(yōu)化?
目前博世正在如火如荼地進行數(shù)字化轉(zhuǎn)型探索,生產(chǎn)部門有大量的場景和數(shù)據(jù)等待挖掘,比如產(chǎn)線合理排班,貼片機貼片順序等都有可能涉及到組合最優(yōu)化。
而工程部的業(yè)務(wù)主要是跟設(shè)計相關(guān)的,比如說PCB的布局與布線設(shè)計,機械結(jié)構(gòu)件的設(shè)計等等。這些設(shè)計工作嚴重依賴工程師的經(jīng)驗,似乎很難進行數(shù)字化優(yōu)化。設(shè)計工作就是在滿足一定約束條件下,設(shè)計完成某些功能的過程,對這進行高度抽象,不就是組合最優(yōu)化問題嗎?
在PCB板設(shè)計結(jié)束后,要對板子上的某些元器件進行保護層設(shè)計和保護層噴涂。目前設(shè)計依賴設(shè)計工程師的設(shè)計經(jīng)驗,噴涂路徑依賴產(chǎn)線工程師的經(jīng)驗及其反復調(diào)試,其缺點是依賴專家經(jīng)驗,項目周期長。
如果能根據(jù)組合最優(yōu)化原理開發(fā)一種PCB元器件保護層自動設(shè)計軟件,幫助設(shè)計工程師優(yōu)化保護層設(shè)計,幫助產(chǎn)線工程師優(yōu)化噴涂路徑,提升工作效率,那將是極好的。
于是我們有了下圖設(shè)計:
通過使用我們提供的自動化設(shè)計軟件,項目的交付時間將縮短85%以上。這可以看作是數(shù)字化過程中典型的案例,利用組合最優(yōu)化技術(shù)極大地提升了設(shè)計人員的工作效率,也提升了噴涂的生產(chǎn)效率。
除此之外,還有PCB的設(shè)計工作,如何借助組合最優(yōu)化及AI技術(shù)幫助PCB設(shè)計工程師快速布線和布局是一個有意義但極具挑戰(zhàn)性的問題,這也很值得探索。
總之,組合最優(yōu)化涉及到我們生活的各個方面,掌握組合最優(yōu)化不僅使我們能玩好魔方,而且能豐富我們的生活和工作的思路,更能直接提升工程師的工作效率。
-
工程師
+關(guān)注
關(guān)注
59文章
1571瀏覽量
68562 -
芯片設(shè)計
+關(guān)注
關(guān)注
15文章
1023瀏覽量
54937 -
AI
+關(guān)注
關(guān)注
87文章
31155瀏覽量
269494
原文標題:揭秘組合最優(yōu)化——從魔方到工程設(shè)計
文章出處:【微信號:AE_China_10,微信公眾號:博世汽車電子事業(yè)部】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
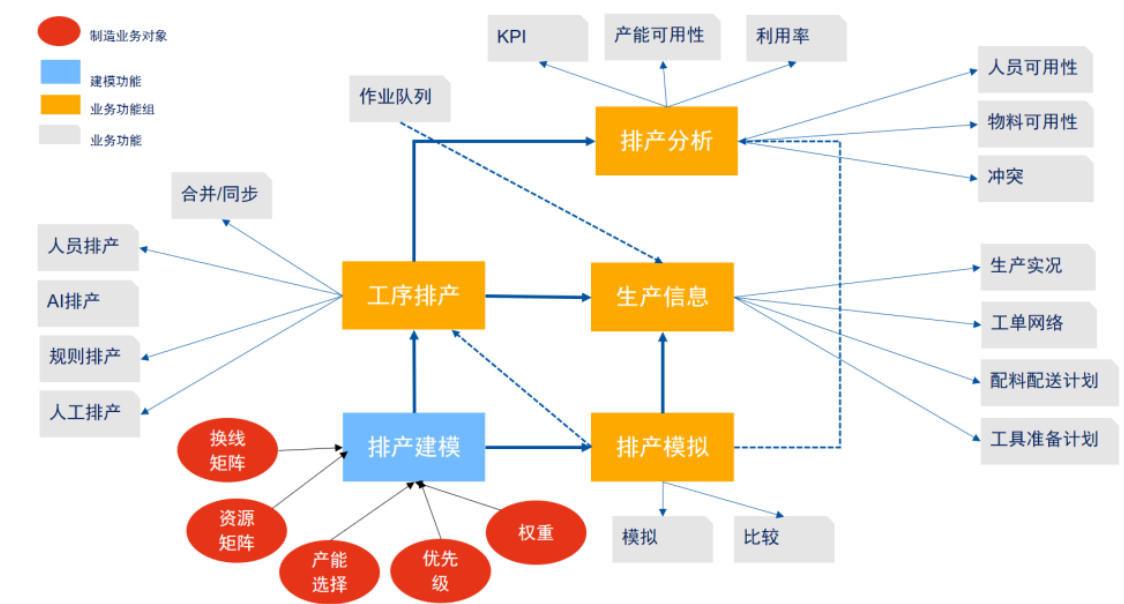
自動排產(chǎn)系統(tǒng):如何實現(xiàn)生產(chǎn)計劃優(yōu)化的關(guān)鍵策略
繼電器組合及組合架的作用
25G/28G重定時器與轉(zhuǎn)接驅(qū)動器在常見應(yīng)用中的最優(yōu)化實現(xiàn)

量子計算場景實用秘籍:開物SDK之“高階函數(shù)降階”
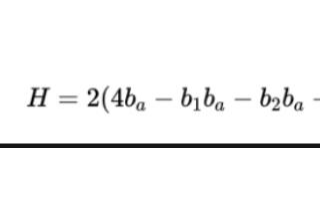
多級運放級聯(lián)如何安排運放放大倍數(shù)才能讓信號質(zhì)量最優(yōu)噪聲小?
優(yōu)化 FPGA HLS 設(shè)計
“本源悟空”真機應(yīng)用之金融科技領(lǐng)域——投資組合優(yōu)化應(yīng)用

組合邏輯控制器的設(shè)計步驟是什么
組合邏輯控制器的工作原理是什么
組合邏輯控制器是用什么實現(xiàn)的
ESP32-WROVER-B 16M固件里的WiFi參數(shù)怎么設(shè)置才算最優(yōu)?
英特爾優(yōu)化AI產(chǎn)品組合,助力微軟Phi-3家族模型
【量子計算機重構(gòu)未來 | 閱讀體驗】第二章關(guān)鍵知識點
如何選擇組合開關(guān)




 什么是組合最優(yōu)化?
什么是組合最優(yōu)化?










評論