量子電路的兩點(diǎn)特殊
Axiom 1: Superposition principle
量子態(tài)是可以疊加的。
而疊加態(tài)的性質(zhì)賦予了量子指數(shù)增長(zhǎng)的可能。
一個(gè)量子比特就是二維Hilbert空間中的向量,兩個(gè)量子比特就是四維Hilbert空間的中向量,三個(gè)就是八維, nn 個(gè)量子比特就是 2n2n 維Hilbert空間中的向量。
另外,需要注意的一點(diǎn)是,即使我只是在一個(gè)量子比特上操作,變化的也是整個(gè)系統(tǒng)。
Axiom 2: Unitary Evolution
量子電路和經(jīng)典另一個(gè)重要的不同就是量子電路是可逆的。
經(jīng)典電路沒(méi)有可逆的要求,比如OR門,如果輸出是1,你知道輸入是什么嗎?(1,1)、(1,0)、(0,1)都有可能,因?yàn)?a target="_blank">信息丟失了,四種輸入的可能,輸出卻只有兩種,信息丟失了。
而量子的操作變換則必須是酉變換,即,可逆,我可以根據(jù)我輸出的信息反推我的輸入。
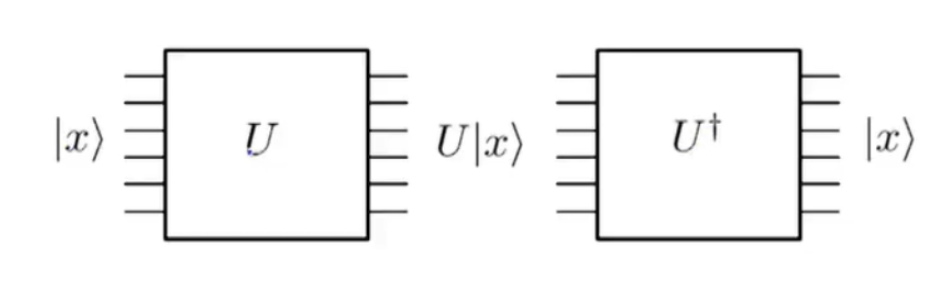
量子可逆電路
經(jīng)典可逆電路其實(shí)是比較容易的。
NOT門,他自己就是可逆的,取反再取反就是本身。
AND門,C-SWAP門其實(shí)就可以代替AND門
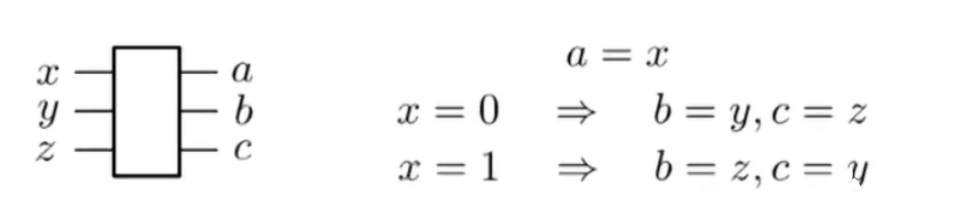
將z固定為0,則c只有在x和y都為1的時(shí)候?yàn)?,其余時(shí)候?yàn)?,滿足AND門的要求。同時(shí)因?yàn)橛衋和b的存在,可以輕易的推導(dǎo)出x,y。
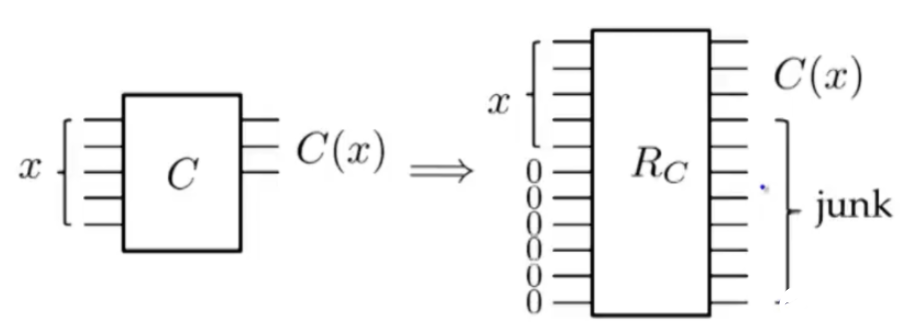
如果將希望能夠從輸出推導(dǎo)出輸入,那么顯然,會(huì)有junk bit(垃圾比特)的存在,即除了我們想要目標(biāo)以外的結(jié)果,不是我們想要的目的,但是是我們推導(dǎo)輸入不可或缺的存在,對(duì)于C-SWAP門來(lái)說(shuō),就是a,b。
junk bit對(duì)于經(jīng)典比特來(lái)說(shuō),就是多出來(lái)的比特而已,但是對(duì)于量子比特來(lái)說(shuō),卻是需要被remove的東西。如果不處理,會(huì)影響后續(xù)的計(jì)算。所以說(shuō),設(shè)計(jì)量子電路,第一個(gè)問(wèn)題其實(shí)不是量子電路能夠比經(jīng)典電路加速多少倍,而是量子電路是否可以做到經(jīng)典電路做到的事。
為什么要移除垃圾比特
對(duì)于經(jīng)典比特來(lái)說(shuō),我不需要的比特,直接不要就可以了。我的后續(xù)操作中不涉及這些垃圾比特就沒(méi)有關(guān)系,但是因?yàn)橛辛孔酉喔傻拇嬖冢绻抑苯硬还芾忍貢?huì)讓后續(xù)的測(cè)量得到完全不一樣的結(jié)果。
例子:
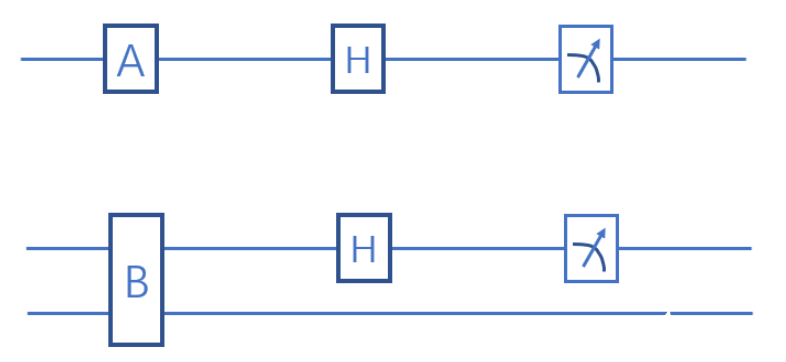
令我們的目標(biāo)函數(shù)是f(x)=x,A是沒(méi)有垃圾比特的情況,即,我們輸入什么輸出什么。而B(niǎo)是有垃圾比特情況,第一個(gè)比特存目標(biāo)答案,f(x)=x,第二個(gè)比特是我們的垃圾比特,假設(shè)這里的垃圾比特是junk(x)=x。
例子A:
在A的情況下,如果我們的輸入是 12√|0?+12√|1?12|0?+12|1? ,經(jīng)過(guò)A門,還是 12√|0?+12√|1?12|0?+12|1? ,在H門后,我們的比特又變成了 |0?|0? ,此時(shí)測(cè)量,得到的結(jié)果一定是 |0?|0? 。
例子B:
在B的情況下,如果我們的輸入是 (12√|0?+12√|1?)|0?(12|0?+12|1?)|0? ,經(jīng)過(guò)A門,則變成了12√|00?+12√|11?12|00?+12|11? ,此時(shí)對(duì)第一個(gè)比特進(jìn)行H門操作,得到結(jié)果 12|00?+12|10?+12|10??12|10?12|00?+12|10?+12|10??12|10? 。此時(shí)對(duì)第一個(gè)比特測(cè)量,得到的結(jié)果是 |0?|0? 或者是 |1?|1? 的概率是一樣的。
因?yàn)橛辛说诙€(gè)比特的存在,所以上述式子中的 ?? 不能直接抵消第一個(gè)比特為 |1?|1? 的可能性,這也就是垃圾比特不得不移除的原因。
如何移除垃圾比特
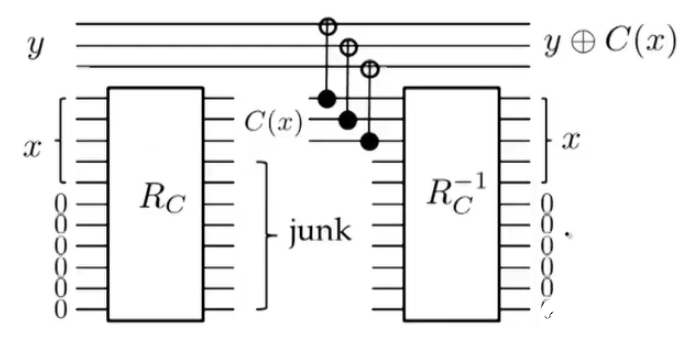
垃圾比特對(duì)后續(xù)有影響,那么將他移除就好了,因?yàn)榱孔拥牟僮魇强赡娴模栽趺磥?lái)的怎么回去。
但是在回去之前,把我們需要的目標(biāo) C(x)C(x) 的量子態(tài)用CNOT門復(fù)制出來(lái)就好。這樣就得到了沒(méi)有垃圾比特的結(jié)果。
可能有人想問(wèn),不是量子態(tài)不能復(fù)制嗎?事實(shí)上,我們并沒(méi)有復(fù)制 C(x)C(x) 的結(jié)果,當(dāng)我們把結(jié)果從原來(lái)的比特上轉(zhuǎn)移到y(tǒng)上后,原來(lái)的比特和垃圾比特又通過(guò)逆操作返回了最初的情況。垃圾比特最初的狀態(tài)是 |0?|0? ,并非疊加態(tài)的情況,量子的糾纏或者相干是因?yàn)橛辛孔盈B加態(tài),不是純態(tài)的原因,而今回到純態(tài),就不在造成影響。
-
量子態(tài)
+關(guān)注
關(guān)注
0文章
8瀏覽量
2149 -
量子電路
+關(guān)注
關(guān)注
0文章
3瀏覽量
1825
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
使用兩點(diǎn)校準(zhǔn)消除ADC失調(diào)和增益誤差
我對(duì) Protues 的兩點(diǎn)困惑 ,求大神
可支持兩點(diǎn)觸摸的四線電阻屏控制IC
如何使用ADS2009找到兩點(diǎn)之間的阻抗
什么是量子點(diǎn)技術(shù)?量子點(diǎn)技術(shù)牛在哪?
基于FPGA的兩點(diǎn)非均勻校正模塊的設(shè)計(jì)與實(shí)現(xiàn)
延長(zhǎng)電池使用壽命注意兩點(diǎn)
電阻測(cè)試:四點(diǎn)法與兩點(diǎn)法的原理與差異(簡(jiǎn)單)
對(duì)量子點(diǎn)技術(shù)的分析
物聯(lián)網(wǎng)大規(guī)模落地最關(guān)鍵的兩點(diǎn)是:標(biāo)準(zhǔn)統(tǒng)一和信息安全
使用Labview解決兩點(diǎn)間實(shí)際距離轉(zhuǎn)換
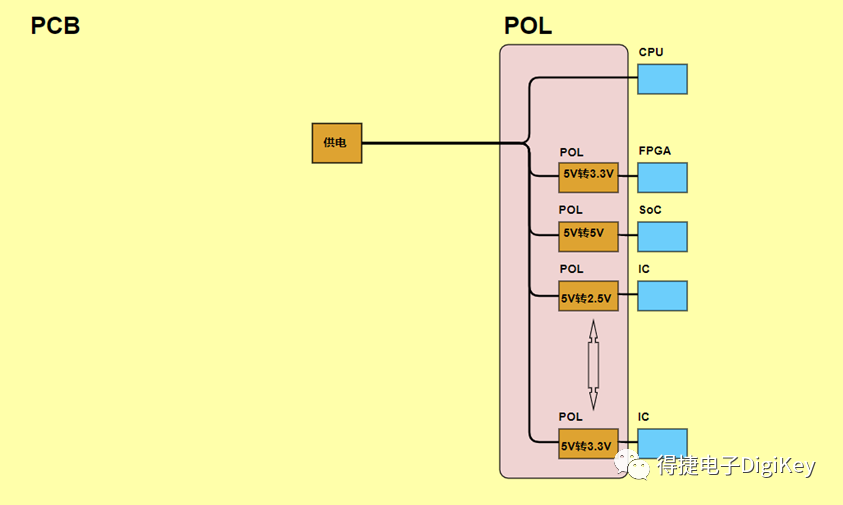
POL負(fù)載點(diǎn)電源設(shè)計(jì)中有何訣竅?有兩點(diǎn)很關(guān)鍵,你必須知道




 量子電路的兩點(diǎn)特殊分析
量子電路的兩點(diǎn)特殊分析










評(píng)論