計算機中的標(biāo)量機是指只是一個數(shù)一個數(shù)地進行計算的加工處理方法，區(qū)別于向量機能夠?qū)σ慌鷶?shù)據(jù)同時進行加工處理。標(biāo)量機比向量機的運算速度慢，因此，向量機更適合于演算數(shù)據(jù)量多的大型科學(xué)、工程計算問題。

計算機（computer）俗稱電腦，是一種用于高速計算的電子計算機器，可以進行數(shù)值計算，又可以進行邏輯計算，還具有存儲記憶功能。是能夠按照程序運行，自動、高速處理海量數(shù)據(jù)的現(xiàn)代化智能電子設(shè)備。

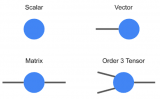
1、標(biāo)量

一個標(biāo)量就是一個單獨的數(shù)，一般用小寫的的變量名稱表示。

2、向量

一個向量就是一列數(shù)，這些數(shù)是有序排列的。用過次序中的索引，我們可以確定每個單獨的數(shù)。通常會賦予向量粗體的小寫名稱。當(dāng)我們需要明確表示向量中的元素時，我們會將元素排列成一個方括號包圍的縱柱：

我們可以把向量看作空間中的點，每個元素是不同的坐標(biāo)軸上的坐標(biāo)。

3、矩陣

矩陣是二維數(shù)組，其中的每一個元素被兩個索引而非一個所確定。我們通常會賦予矩陣粗體的大寫變量名稱，比如A。 如果一個實數(shù)矩陣高度為m，寬度為n，那么我們說 。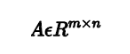

矩陣這東西在機器學(xué)習(xí)中就不要太重要了！實際上，如果我們現(xiàn)在有N個用戶的數(shù)據(jù)，每條數(shù)據(jù)含有M個特征，那其實它對應(yīng)的就是一個N*M的矩陣呀；再比如，一張圖由16*16的像素點組成，那這就是一個16*16的矩陣了。現(xiàn)在才發(fā)現(xiàn)，我們大一學(xué)的矩陣原理原來這么的有用！要是當(dāng)時老師講課的時候先普及一下，也不至于很多同學(xué)學(xué)矩陣的時候覺得莫名其妙了。

4、張量

幾何代數(shù)中定義的張量是基于向量和矩陣的推廣，通俗一點理解的話，我們可以將標(biāo)量視為零階張量，矢量視為一階張量，那么矩陣就是二階張量。

例如，可以將任意一張彩色圖片表示成一個三階張量，三個維度分別是圖片的高度、寬度和色彩數(shù)據(jù)。將這張圖用張量表示出來，就是最下方的那張表格：

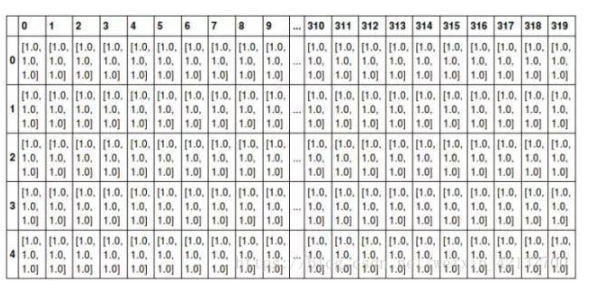
其中表的橫軸表示圖片的寬度值，這里只截取0~319；表的縱軸表示圖片的高度值，這里只截取0~4；表格中每個方格代表一個像素點，比如第一行第一列的表格數(shù)據(jù)為［1.0，1.0，1.0］，代表的就是RGB三原色在圖片的這個位置的取值情況（即R=1.0，G=1.0，B=1.0）。

當(dāng)然我們還可以將這一定義繼續(xù)擴展，即：我們可以用四階張量表示一個包含多張圖片的數(shù)據(jù)集，這四個維度分別是：圖片在數(shù)據(jù)集中的編號，圖片高度、寬度，以及色彩數(shù)據(jù)。

張量在深度學(xué)習(xí)中是一個很重要的概念，因為它是一個深度學(xué)習(xí)框架中的一個核心組件，后續(xù)的所有運算和優(yōu)化算法幾乎都是基于張量進行的。