三維點云對于多視角和圖形學的表示，合成和重建高質量、高分辨的點云具有重要的意義。雖然近年來在基于點云的判別模型上取得了一系列進展，但在生成模型方面卻還存在著諸多挑戰。

為了實現對于生成模型的理解和應用，來自康奈爾大學和英偉達的研究人員提出了一種基于概率框架的三維點云生成模型PointFlow，通過為分布的分布建模，分別建立形狀的分布和給定形狀下點云的分布，來實現對于形狀的采樣以及給定形狀下任意點云的采樣過程。

作為三維數據的重要形式，點云由于較高的分辨率和對復雜細節更好的表達越來越受到研究人員的青睞。有效的點云生成模型將為重建和超分辨等點云合成任務帶來較大的促進作用。但由于點云復雜的形狀使得生成模型的研究較為緩慢，需要利用概率的方式重新審視點云生成模型的學習過程。

例如，一架飛機的點云可以看做是從飛機對應表面上采樣而得到的點；而這把飛機的曲面則可以視為從飛機形狀的分布中采樣得到的一個特定的形狀。為了生成點云我們需要對分布的分布進行建模，也就是說不僅需要為形狀分布進行建模，同時需要對特定形狀下的點云進行建模。

在研究人員提出的PointFlow中，對于形狀的分布和給定形狀下點的分布進行了建模。

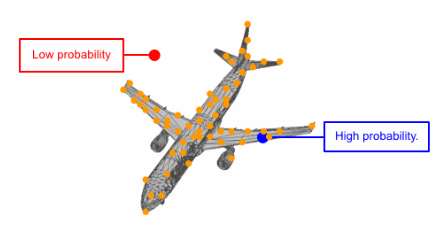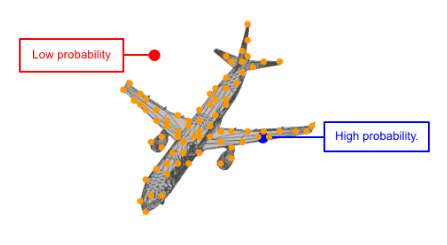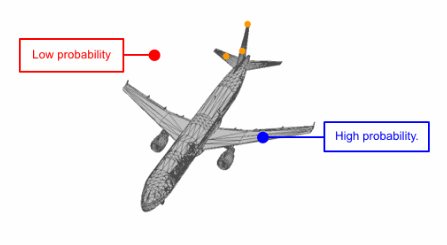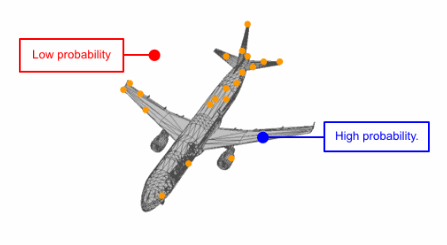
研究人員通過先驗分布3D點的可逆參數化變換代替了直接對點云分布的建模。這意味著在給定模型的情況下，首先從通用的高斯先驗中進行采樣，而后基于參數變換將他們移動到與目標形狀對應的新位置，使得參數化的變化和變量的分布都可以利用這一模型進行描述。

更重要的是，這種模型還帶來了更強大的表達能力。在可以估計概率密度、提升變分下限的同時，還可以避免由GANs帶來的復雜訓練。

在三維點云的學習過程中，我們不經需要從某一類的一系列形狀中進行形狀采樣，同時也需要針對某一形狀對其表面上的點進行采樣(均勻分布)。這一研究的目標在于學習形狀的分布和點的分布。研究人員利用連續歸一化流(continuous normalizing flow，CNF)來為給定形狀下點的分布進行建模。

連續歸一化流可以視為三維歐式空間中的向量場，它可以通過對某一通用的先驗分布進行轉換(例如高斯分布)推導出點云的分布。連續歸一化流是一系列可逆的映射，可以將已知的初始化分布映射到更為復雜的分布上去。通過一系列可逆的變換f來表示，這些變換同樣可以利用神經網絡來實現。

為了從這一推導出的點云中采樣，研究人員首先從通用的先驗分布中進行采樣，然后將這些采樣點移動到矢量場(連續歸一化流)中去。此外連續歸一化流是可逆的，這使得計算精確的似然成為可能。下圖展示了一個從先驗分布到特定形狀點的過程。

隨后研究人員利用參數化的方法將每一個歸一化流用隱空間變量來進行表示，使得對于形狀分布的建模被約化成了對于隱變量的建模。最終的生成模型包含了針對形狀和針對點分布的雙重連續歸一化流。

在訓練過程中，得益于連續歸一化流的可逆性帶來的似然計算，端到端穩定地訓練GANs成為可能。訓練的過程中需要基于變分自編碼器定義三種不同的模塊，分別是講點云編程成形狀表示z的編碼器Q(z|X)、形狀表示的先驗P(z)、以及在給定形狀表達下為點云分布建模的解碼器P(z|X),下圖展示了模型的訓練和推理過程。

在訓練階段，針對給定的點云X編碼器將得到對于形狀的后驗表示，并從中采樣出形狀的表示z，隨后通過z計算出兩方面的損失。一方面利用逆CNF計算出先驗分布并與w進行損失計算Lprior；另一方面利用另一個CNF，G的逆計算重建出似然的損失Lrecon。

同時還需要計算后驗概率的交叉熵Lent。在測試階段，利用F和G即可。首先從高斯先驗中進行采樣并利用F變換到對應的形狀表示z上，然后在3D高斯先驗上進行采樣并基于形狀的采樣z通過G得到進行轉換得到最終的點云。

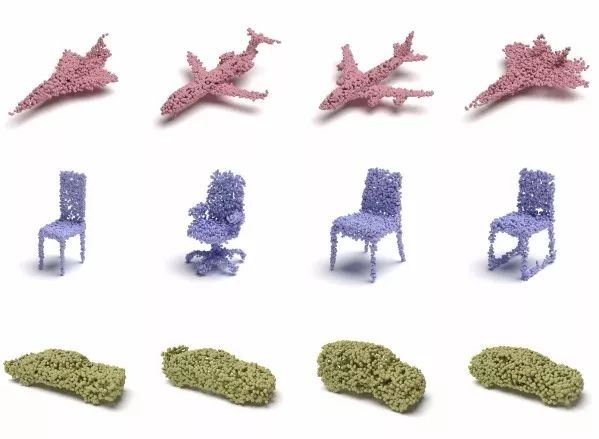
最終利用這種方法生成了一系列點云，可以采樣出各種不同的形狀，得到任意數量的點云。

下圖展示了多個形狀的生成過程，首先需要學習出某類形狀對應的空間，并從形狀空間中得到一個隱變量，隨后利用點的CNF，更加隱變量進行轉換，最后從歸一化分布中采樣的點就被轉換到了目標形狀上了：

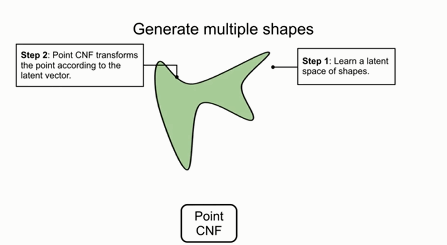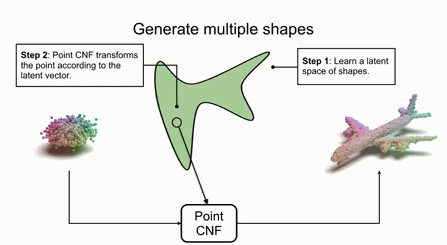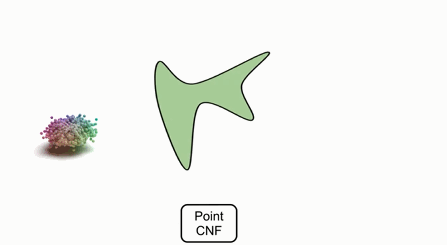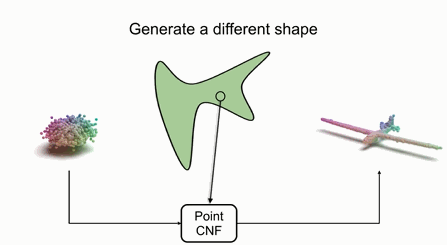
如果需要生成不同的形狀，只需要在隱空間中指定不同的隱變量，并對點進行變換即可。

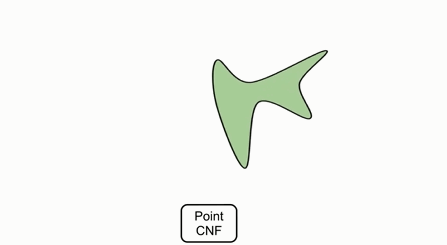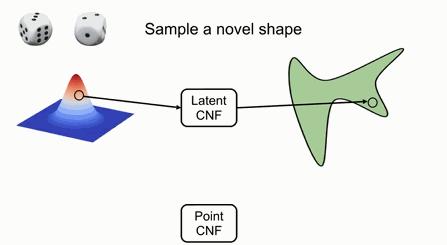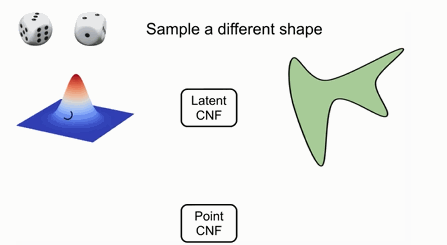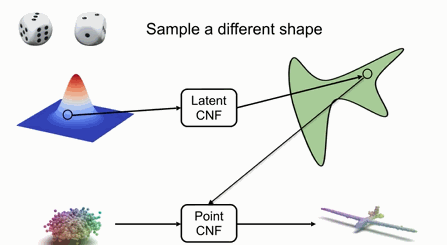
如果要采樣出新的形狀或不同的形狀，可以利用隨機變量采樣隱空間中CNF，并利用隱空間中對應的變量來對輸入的點進行變換。